Newton's method

Newton's method, also known as Newton-Raphson's method, is a very famous and widely used method for solving nonlinear algebraic equations. Compared to the other methods we will consider, it is generally the fastest one (usually by far). It does not guarantee that an existing solution will be found, however.

A fundamental idea of numerical methods for nonlinear equations is to construct a series of linear equations (since we know how to solve linear equations) and hope that the solutions of these linear equations bring us closer and closer to the solution of the nonlinear equation. The idea will be clearer when we present Newton's method and the secant method.

Deriving and implementing Newton's method

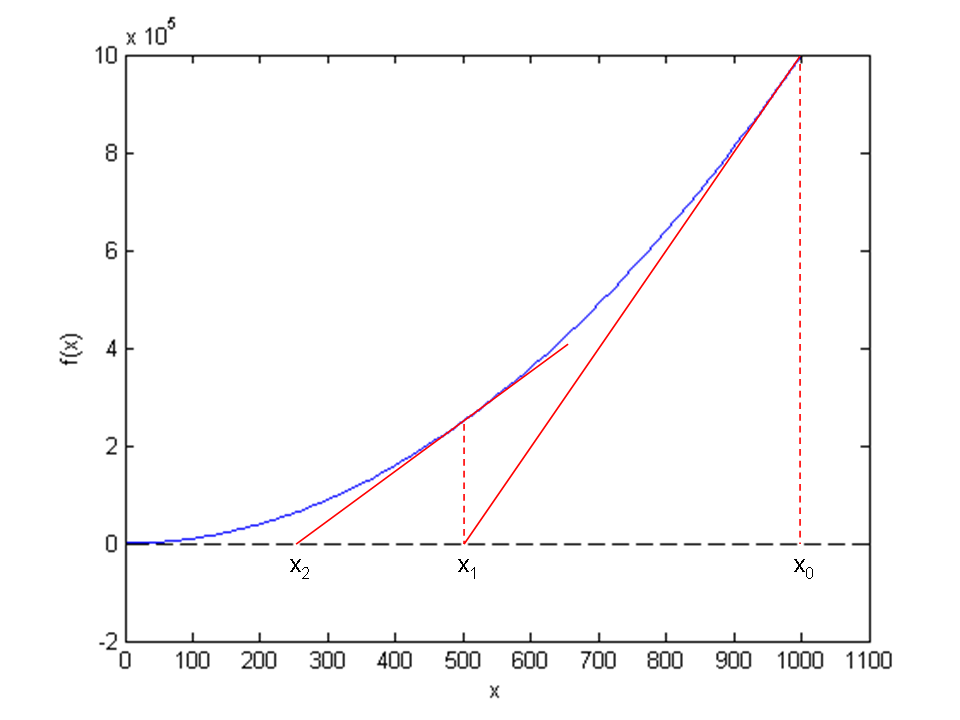
Figure 62 shows the $ f(x) $ function in our model equation $ x^2-9=0 $. Numerical methods for algebraic equations require us to guess at a solution first. Here, this guess is called $ x_0 $. The fundamental idea of Newton's method is to approximate the original function $ f(x) $ by a straight line, i.e., a linear function, since it is straightforward to solve linear equations. There are infinitely many choices of how to approximate $ f(x) $ by a straight line. Newton's method applies the tangent of $ f(x) $ at $ x_0 $, see the rightmost tangent in Figure 62. This linear tangent function crosses the $ x $ axis at a point we call $ x_1 $. This is (hopefully) a better approximation to the solution of $ f(x)=0 $ than $ x_0 $. The next fundamental idea is to repeat this process. We find the tangent of $ f $ at $ x_1 $, compute where it crosses the $ x $ axis, at a point called $ x_2 $, and repeat the process again. Figure 62 shows that the process brings us closer and closer to the left. It remains, however, to see if we hit $ x=3 $ or come sufficiently close to this solution.

Figure 62: Illustrates the idea of Newton's method with $ f(x) = x^2 - 9 $, repeatedly solving for crossing of tangent lines with the $ x $ axis.

How do we compute the tangent of a function $ f(x) $ at a point $ x_0 $? The tangent function, here called $ \tilde f(x) $, is linear and has two properties:

the slope equals to $ f'(x_0) $
the tangent touches the $ f(x) $ curve at $ x_0 $

So, if we write the tangent function as $ \tilde f(x)=ax+b $, we must require $ \tilde f'(x_0)=f'(x_0) $ and $ \tilde f(x_0)=f(x_0) $, resulting in $$ \tilde f(x) = f(x_0) + f'(x_0)(x - x_0)\thinspace . $$

The key step in Newton's method is to find where the tangent crosses the $ x $ axis, which means solving $ \tilde f(x)=0 $: $$ \tilde f(x)=0\quad\Rightarrow\quad x = x_0 - \frac{f(x_0)}{f'(x_0)} \thinspace .$$ This is our new candidate point, which we call $ x_1 $: $$ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\thinspace . $$ With $ x_0 = 1000 $, we get $ x_1 \approx 500 $, which is in accordance with the graph in Figure 62. Repeating the process, we get $$ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)}\approx 250\thinspace . $$

The general scheme of Newton's method may be written as $$ \begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)},\quad n=0,1,2,\ldots \tag{6.1} \end{equation} $$ The computation in (6.1) is repeated until $ f\left(x_n\right) $ is close enough to zero. More precisely, we test if $ |f(x_n)| < \epsilon $, with $ \epsilon $ being a small number.

We moved from 1000 to 250 in two iterations, so it is exciting to see how fast we can approach the solution $ x=3 $. A computer program can automate the calculations. Our first try at implementing Newton's method is in a function naive_Newton:

def naive_Newton(f, dfdx, x, eps):
    while abs(f(x)) > eps:
        x = x - float(f(x))/dfdx(x)
    return x

The argument x is the starting value, called $ x_0 $ in our previous mathematical description. We use float(f(x)) to ensure that an integer division does not happen by accident if f(x) and dfdx(x) both are integers for some x.

To solve the problem $ x^2=9 $ we also need to implement

def f(x):
    return x**2 - 9

def dfdx(x):
    return 2*x

print naive_Newton(f, dfdx, 1000, 0.001)

Why not use an array for the $ x $ approximations? Newton's method is normally formulated with an iteration index $ n $, $$ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\thinspace .$$ Seeing such an index, many would implement this as

x[n+1] = x[n] - f(x[n])/dfdx(x[n])

Such an array is fine, but requires storage of all the approximations. In large industrial applications, where Newton's method solves millions of equations at once, one cannot afford to store all the intermediate approximations in memory, so then it is important to understand that the algorithm in Newton's method has no more need for $ x_n $ when $ x_{n+1} $ is computed. Therefore, we can work with one variable x and overwrite the previous value:

x = x - f(x)/dfdx(x)

Running naive_Newton(f, dfdx, 1000, eps=0.001) results in the approximate solution 3.000027639. A smaller value of eps will produce a more accurate solution. Unfortunately, the plain naive_Newton function does not return how many iterations it used, nor does it print out all the approximations $ x_0,x_1,x_2,\ldots $, which would indeed be a nice feature. If we insert such a printout, a rerun results in

500.0045
250.011249919
125.02362415
62.5478052723
31.3458476066
15.816483488
8.1927550496
4.64564330569
3.2914711388
3.01290538807
3.00002763928

We clearly see that the iterations approach the solution quickly. This speed of the search for the solution is the primary strength of Newton's method compared to other methods.

Making a more efficient and robust implementation

The naive_Newton function works fine for the example we are considering here. However, for more general use, there are some pitfalls that should be fixed in an improved version of the code. An example may illustrate what the problem is: let us solve $ \tanh(x)=0 $, which has solution $ x=0 $. With $ |x_0|\leq 1.08 $ everything works fine. For example, $ x_0 $ leads to six iterations if $ \epsilon=0.001 $:

-1.05895313436
0.989404207298
-0.784566773086
0.36399816111
-0.0330146961372
2.3995252668e-05

Adjusting $ x_0 $ slightly to 1.09 gives division by zero! The approximations computed by Newton's method become

-1.09331618202
1.10490354324
-1.14615550788
1.30303261823
-2.06492300238
13.4731428006
-1.26055913647e+11

The division by zero is caused by $ x_7=-1.26055913647\cdot 10^{11} $, because $ \tanh(x_7) $ is 1.0 to machine precision, and then $ f'(x)=1 - \tanh(x)^2 $ becomes zero in the denominator in Newton's method.

The underlying problem, leading to the division by zero in the above example, is that Newton's method diverges: the approximations move further and further away from $ x=0 $. If it had not been for the division by zero, the condition in the while loop would always be true and the loop would run forever. Divergence of Newton's method occasionally happens, and the remedy is to abort the method when a maximum number of iterations is reached.

Another disadvantage of the naive_Newton function is that it calls the $ f(x) $ function twice as many times as necessary. This extra work is of no concern when $ f(x) $ is fast to evaluate, but in large-scale industrial software, one call to $ f(x) $ might take hours or days, and then removing unnecessary calls is important. The solution in our function is to store the call f(x) in a variable (f_value) and reuse the value instead of making a new call f(x).

To summarize, we want to write an improved function for implementing Newton's method where we

avoid division by zero
allow a maximum number of iterations
avoid the extra evaluation to $ f(x) $

A more robust and efficient version of the function, inserted in a complete program Newtons_method.py for solving $ x^2 - 9 = 0 $, is listed below.

def Newton(f, dfdx, x, eps):
    f_value = f(x)
    iteration_counter = 0
    while abs(f_value) > eps and iteration_counter < 100:
        try:
            x = x - float(f_value)/dfdx(x)
        except ZeroDivisionError:
            print "Error! - derivative zero for x = ", x
            sys.exit(1)     # Abort with error

        f_value = f(x)
        iteration_counter += 1

    # Here, either a solution is found, or too many iterations
    if abs(f_value) > eps:
        iteration_counter = -1
    return x, iteration_counter

def f(x):
    return x**2 - 9

def dfdx(x):
    return 2*x

solution, no_iterations = Newton(f, dfdx, x=1000, eps=1.0e-6)

if no_iterations > 0:    # Solution found
    print "Number of function calls: %d" % (1 + 2*no_iterations)
    print "A solution is: %f" % (solution)
else:
    print "Solution not found!"

Handling of the potential division by zero is done by a try-except construction. Python tries to run the code in the try block. If anything goes wrong here, or more precisely, if Python raises an exception caused by a problem (such as division by zero, array index out of bounds, use of undefined variable, etc.), the execution jumps immediately to the except block. Here, the programmer can take appropriate actions. In the present case, we simply stop the program. (Professional programmers would avoid calling sys.exit inside a function. Instead, they would raise a new exception with an informative error message, and let the calling code have another try-except construction to stop the program.)

The division by zero will always be detected and the program will be stopped. The main purpose of our way of treating the division by zero is to give the user a more informative error message and stop the program in a gentler way.

Calling sys.exit with an argument different from zero (here 1) signifies that the program stopped because of an error. It is a good habit to supply the value 1, because tools in the operating system can then be used by other programs to detect that our program failed.

To prevent an infinite loop because of divergent iterations, we have introduced the integer variable iteration_counter to count the number of iterations in Newton's method. With iteration_counter we can easily extend the condition in the while such that no more iterations take place when the number of iterations reaches 100. We could easily let this limit be an argument to the function rather than a fixed constant.

The Newton function returns the approximate solution and the number of iterations. The latter equals $ -1 $ if the convergence criterion $ |f(x)| < \epsilon $ was not reached within the maximum number of iterations. In the calling code, we print out the solution and the number of function calls. The main cost of a method for solving $ f(x)=0 $ equations is usually the evaluation of $ f(x) $ and $ f'(x) $, so the total number of calls to these functions is an interesting measure of the computational work. Note that in function Newton there is an initial call to $ f(x) $ and then one call to $ f $ and one to $ f' $ in each iteration.

Running Newtons_method.py, we get the following printout on the screen:

Number of function calls: 25
A solution is: 3.000000

As we did with the integration methods in the chapter Computing integrals, we will collect our solvers for nonlinear algebraic equations in a separate file named nonlinear_solvers.py for easy import and use. The first function placed in this file is then Newton.

The Newton scheme will work better if the starting value is close to the solution. A good starting value may often make the difference as to whether the code actually finds a solution or not. Because of its speed, Newton's method is often the method of first choice for solving nonlinear algebraic equations, even if the scheme is not guaranteed to work. In cases where the initial guess may be far from the solution, a good strategy is to run a few iterations with the bisection method (see the chapter The bisection method) to narrow down the region where $ f $ is close to zero and then switch to Newton's method for fast convergence to the solution.

Newton's method requires the analytical expression for the derivative $ f'(x) $. Derivation of $ f'(x) $ is not always a reliable process by hand if $ f(x) $ is a complicated function. However, Python has the symbolic package SymPy, which we may use to create the required dfdx function. In our sample problem, the recipe goes as follows:

from sympy import *
x = symbols('x')             # define x as a mathematical symbol
f_expr = x**2 - 9            # symbolic expression for f(x)
dfdx_expr = diff(f_expr, x)  # compute f'(x) symbolically
# Turn f_expr and dfdx_expr into plain Python functions
f = lambdify([x],     # argument to f
             f_expr)  # symbolic expression to be evaluated
dfdx = lambdify([x], dfdx_expr)
print dfdx(5)         # will print 10

The nice feature of this code snippet is that dfdx_expr is the exact analytical expression for the derivative, 2*x, if you print it out. This is a symbolic expression so we cannot do numerical computing with it, but the lambdify constructions turn symbolic expressions into callable Python functions.

The next method is the secant method, which is usually slower than Newton's method, but it does not require an expression for $ f'(x) $, and it has only one function call per iteration.