Exercises
Exercise 30: Hand calculations for the trapezoidal method
Compute by hand the area composed of two trapezoids (of equal width) that
approximates the integral \( \int_1^3 2x^3dx \). Make a test function
that calls the trapezoidal function in trapezoidal.py
and compares the return value with the hand-calculated value.
The code may be written as follows
from trapezoidal import trapezoidal
def test_trapezoidal():
def f(x):
return 2*x**3
a = 1; b = 3
n = 2
numerical = trapezoidal(f, a, b, n)
hand = 44.0
error = abs(numerical - hand)
tol = 1E-14
assert error < tol, error
test_trapezoidal()
Filename: trapezoidal_test_func.py.
Exercise 31: Hand calculations for the midpoint method
Compute by hand the area composed of two rectangles (of equal width) that
approximates the integral \( \int_1^3 2x^3dx \). Make a test function
that calls the midpoint function in midpoint.py
and compares the return value with the hand-calculated value.
The code may be written as follows
from midpoint import midpoint
def test_midpoint():
def f(x):
return 2*x**3
a = 1; b = 3;
n = 2
numerical = midpoint(f, a, b, n)
hand = 38.0
error = abs(numerical - hand)
tol = 1E-14
assert error < tol, error
test_midpoint()
Filename: midpoint_test_func.py.
Exercise 32: Compute a simple integral
Apply the trapezoidal and midpoint functions to compute
the integral \( \int_2^6 x(x -1)dx \) with 2 and 100 subintervals.
Compute the error too.
The code may be written as follows
from trapezoidal import trapezoidal
from midpoint import midpoint
def f(x):
return x*(x-1)
a = 2; b = 6;
n = 100
numerical_trap = trapezoidal(f, a, b, n)
numerical_mid = midpoint(f, a, b, n)
# Compute exact integral by sympy
import sympy as sp
x = sp.symbols('x')
F = sp.integrate(f(x))
exact = F.subs(x, b) - F.subs(x, a)
exact = exact.evalf()
error_trap = abs(numerical_trap - exact)
error_mid = abs(numerical_mid - exact)
print 'For n = %d, we get:' % (n)
print 'Numerical trapezoid: %g , Error: %g' % \
(numerical_trap,error_trap)
print 'Numerical midpoint: %g , Error: %g' % \
(numerical_mid,error_mid)
In the code, we have taken the opportunity to show
how commenting often is used to switch between two
code fragments, typically single statements. The
alternatives n = 2 and n = 100 are switched by
removing/adding the comment sign #, before running
the code anew. Another alternative would of course be
to ask the user for the value of n.
Running the program with n = 2, produces the following printout:
For n = 2, we get:
Numerical trapezoid: 56 , Error: 2.667
Numerical midpoint: 52 , Error: 1.333
while running it with n = 100 gives:
For n = 100, we get:
Numerical trapezoid: 53.3344 , Error: 0.0014
Numerical midpoint: 53.3328 , Error: 0.0002
The analytical value of the integral is 53.333 (rounded).
Filename: integrate_parabola.py.
Exercise 33: Hand-calculations with sine integrals
We consider integrating the sine function: \( \int_0^b \sin (x)dx \).
a) Let \( b=\pi \) and use two intervals in the trapezoidal and midpoint method. Compute the integral by hand and illustrate how the two numerical methods approximates the integral. Compare with the exact value.
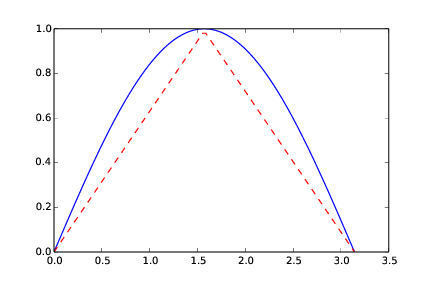
Analytically, the integral computes to 2. By hand, with the trapezoidal method, we get 1.570. Graphically (Figure 10), it is clear that the numerical approach will have to under-estimate the true result.
The area under the blue graph in Figure 10 corresponds to the "true" area under the graph of the integrand. The area under the red graph corresponds to what you get with the trapezoidal method and two intervals.
Figure 10: The integral computed with the trapezoidal method (n = 2).
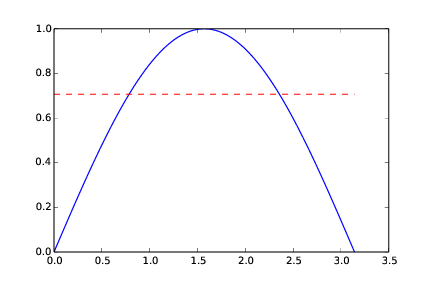
By hand, with the midpoint method, we get 2.221. Graphically (Figure 11), we might see that the numerical approach will have to over-estimate the true result. Again, the area under the blue graph in Figure 11 corresponds to the "true" area under the graph of the integrand. The area under the red graph corresponds to what you get with the midpoint method and two intervals.
Figure 11: The integral computed with the midpoint method (n = 2).
b) Do a) when \( b=2\pi \).
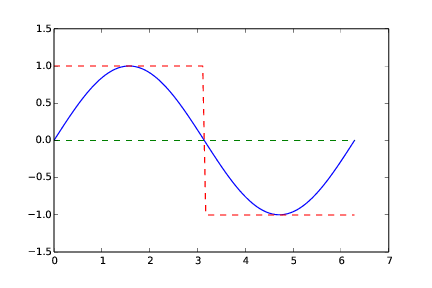
Analytically, the integral computes to zero. In this case, both numerical methods will correctly calculate the integral to zero even with just two intervals! Graphically, we see that they arrive at zero for "different reasons". The trapezoidal method constructs both its trapezoids by use of the function (integrand) value at the midpoint of the whole interval. However, there the integrand crosses the x-axis, i.e. it evaluates to zero. The "area" computed by the trapezoidal method becomes the zero area located "between" the green graph and the x-axis in Figure 12. The midpoint method computes the areas of two rectangles (red graph in Figure 12), but since the signs of these equal areas differ, they add to zero.
Figure 12: The integral computed with the trapezoidal and midpoint method (n = 2).
Filename: integrate_sine.pdf.
Exercise 34: Make test functions for the midpoint method
Modify the file test_trapezoidal.py such that the
three tests are applied to the function midpoint implementing
the midpoint method for integration.
Note that also the midpoint method will do an exact (to within machine precision) integration when the integrand is a straight line. This is so, since the errors from each rectangle will cancel. The code reads:
from midpoint import midpoint
def test_midpoint_one_exact_result():
"""Compare one hand-computed result."""
from math import exp
v = lambda t: 3*(t**2)*exp(t**3)
n = 2
numerical = midpoint(v, 0, 1, n)
exact = 1.3817914596908085
err = abs(exact - numerical)
tol = 1E-14
assert err < tol, err
def test_midpoint_linear():
"""Check that linear functions are integrated exactly"""
# ...they should, since errros from each rectangle cancel
f = lambda x: 6*x - 4
F = lambda x: 3*x**2 - 4*x # Anti-derivative
a = 1.2; b = 4.4
exact = F(b) - F(a)
tol = 1E-14
for n in 2, 20, 21:
numerical = midpoint(f, a, b, n)
err = abs(exact - numerical)
assert err < tol, 'n = %d, err = %g' % (n,err)
def test_midpoint_conv_rate():
"""Check empirical convergence rates against the expected -2."""
from math import exp
v = lambda t: 3*(t**2)*exp(t**3)
V = lambda t: exp(t**3)
a = 1.1; b = 1.9
r = convergence_rates(v, V, a, b, 14)
print r
tol = 0.01
assert (abs(r[-1]) - 2) < tol, r[-4:]
def convergence_rates(f, F, a, b, num_experiments=14):
from math import log
from numpy import zeros
exact = F(b) - F(a)
n = zeros(num_experiments, dtype=int)
E = zeros(num_experiments)
r = zeros(num_experiments-1)
for i in range(num_experiments):
n[i] = 2**(i+1)
numerical = midpoint(f, a, b, n[i])
E[i] = abs(exact - numerical)
if i > 0:
r_im1 = log(E[i]/E[i-1])/log(float(n[i])/n[i-1])
r[i-1] = float('%.2f' % r_im1) # Truncate, two decimals
return r
test_midpoint_one_exact_result()
test_midpoint_linear()
test_midpoint_conv_rate()
Filename: test_midpoint.py.
Exercise 35: Explore rounding errors with large numbers
The trapezoidal method integrates linear functions exactly, and this
property was used in the test function test_trapezoidal_linear in the file
test_trapezoidal.py. Change the function used in
the section Proper test procedures to \( f(x)=6\cdot 10^8 x - 4\cdot 10^6 \)
and rerun the test. What happens? How must you change the test
to make it useful? How does the convergence rate test behave? Any need
for adjustment?
With the new function given, we get the error message that includes:
AssertionError: n = 2, err = 9.53674e-07
The numerical calculation then obviously differs from the exact value by
more than what is specified in the tolerance tol. We may understand this
by considering the new function, i.e., \( f(x)=6\cdot 10^8 x - 4\cdot 10^6 \).
Any rounding error in \( x \) will get magnified big time by the factor \( 6\cdot 10^8 \) in front,
i.e. the slope of the line. This makes the numerical calculation more inaccurate than previously.
To fix this problem, we have several options. One possibility is to relax the tolerance, but
this is not very satisfactory. After all, the calculation is supposed to be "exact" for a straight
line. Another alternative is to introduce a new integration variable such
that we scale the interval \( [a,b] \) into \( [\frac{a}{6\cdot 10^8},\frac{b}{6\cdot 10^8}] \), as
this will neutralize the huge factor in front of \( x \), bringing the accuracy back to where it was previously. This
alternative is implemented in
test_trapezoidal2.py.
from trapezoidal import trapezoidal
def test_trapezoidal_linear_scale():
"""Check that linear functions are integrated exactly"""
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
#a = 1.2; b = 4.4
a = 1.2/6E8; b = 4.4/6E8 # Scale interval down
exact = F(b) - F(a)
tol = 1E-14
for n in 2, 20, 21:
numerical = trapezoidal(f, a, b, n)
err = abs(exact - numerical)
msg = 'n = %d, err = %g' % (n, err)
assert err < tol, msg
print msg
A third alternative is to use the module decimal that comes with Python, which
allows number precision to be altered by the programmer. An alternative,
better suited for numerical computing, is the mpmath module in SymPy (since
it supports standard mathematical functions such as sin and cos with
arbitrary precision, while decimal can only the standard arithmetics with
arbitrary precision).
from trapezoidal import trapezoidal
def test_trapezoidal_linear_scale():
"""Check that linear functions are integrated exactly"""
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
#a = 1.2; b = 4.4
a = 1.2/6E8; b = 4.4/6E8 # Scale interval down
exact = F(b) - F(a)
tol = 1E-14
for n in 2, 20, 21:
numerical = trapezoidal(f, a, b, n)
err = abs(exact - numerical)
msg = 'n = %d, err = %g' % (n, err)
assert err < tol, msg
print msg
def test_trapezoidal_linear_reldiff():
"""
Check that linear functions are integrated exactly.
Use relative and not absolute difference.
"""
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
a = 1.2; b = 4.4 # Scale interval down
exact = F(b) - F(a)
tol = 1E-14
for n in 2, 20, 21:
numerical = trapezoidal(f, a, b, n)
err = abs(exact - numerical)/exact
msg = 'n = %d, err = %g' % (n, err)
assert err < tol, msg
print msg
def test_trapezoidal_conv_rate():
"""Check empirical convergence rates against the expected -2."""
#from math import exp
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
a = 1.1; b = 1.9
r = convergence_rates(f, F, a, b, 14)
print r
tol = 0.01
assert abs(abs(r[-1]) - 2) < tol, r[-4:]
def convergence_rates(f, F, a, b, num_experiments=14):
from math import log
from numpy import zeros
exact = F(b) - F(a)
n = zeros(num_experiments, dtype=int)
E = zeros(num_experiments)
r = zeros(num_experiments-1)
for i in range(num_experiments):
n[i] = 2**(i+1)
numerical = trapezoidal(f, a, b, n[i])
E[i] = abs(exact - numerical)
print E[i]
if i > 0:
r_im1 = log(E[i]/E[i-1])/log(float(n[i])/n[i-1])
r[i-1] = float('%.2f' % r_im1) # Truncate, two decimals
return r
test_trapezoidal_linear_scale()
test_trapezoidal_linear_reldiff()
test_trapezoidal_conv_rate()
The best alternative, however, is to consider relative differences instead
of absolute differences. That is, we compute (exact - numerical)/exact
instead of just exact - numerical. This relative error is \( 10^{-16} \)
even if we compute with very big numbers.
def test_trapezoidal_linear_reldiff():
"""
Check that linear functions are integrated exactly.
Use relative and not absolute difference.
"""
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
a = 1.2; b = 4.4 # Scale interval down
exact = F(b) - F(a)
tol = 1E-14
for n in 2, 20, 21:
numerical = trapezoidal(f, a, b, n)
err = abs(exact - numerical)/exact
msg = 'n = %d, err = %g' % (n, err)
assert err < tol, msg
print msg
def test_trapezoidal_conv_rate():
"""Check empirical convergence rates against the expected -2."""
#from math import exp
f = lambda x: 6E8*x - 4E6
F = lambda x: 3E8*x**2 - 4E6*x # Anti-derivative
a = 1.1; b = 1.9
r = convergence_rates(f, F, a, b, 14)
print r
tol = 0.01
assert abs(abs(r[-1]) - 2) < tol, r[-4:]
def convergence_rates(f, F, a, b, num_experiments=14):
from math import log
from numpy import zeros
exact = F(b) - F(a)
n = zeros(num_experiments, dtype=int)
E = zeros(num_experiments)
r = zeros(num_experiments-1)
for i in range(num_experiments):
n[i] = 2**(i+1)
numerical = trapezoidal(f, a, b, n[i])
E[i] = abs(exact - numerical)
print E[i]
if i > 0:
r_im1 = log(E[i]/E[i-1])/log(float(n[i])/n[i-1])
r[i-1] = float('%.2f' % r_im1) # Truncate, two decimals
return r
Computing convergence rates is not meaningful in this test, because the error is mathematically zero.
Filename: test_trapezoidal2.py.
Exercise 36: Write test functions for \( \int_0^4\sqrt{x}dx \)
We want to test how the trapezoidal function works for the integral
\( \int_0^4\sqrt{x}dx \). Two of the tests in test_trapezoidal.py
are meaningful for this integral. Compute by hand the result of
using 2 or 3 trapezoids and modify the test_trapezoidal_one_exact_result
function accordingly. Then modify test_trapezoidal_conv_rate
to handle the square root integral.
Adjustments to the code are made according to the remark below and hand calculations are written into the code. The code then reads:
from trapezoidal import trapezoidal
def test_trapezoidal_one_exact_result():
"""Compare one hand-computed result."""
f = lambda x: x**0.5
tol = 1E-14
exact = [4.82842712474619, 5.050258266979605] # n=2, n=3
for n in [2, 3]:
numerical = trapezoidal(f, 0, 4, n)
err = abs(exact[n-2] - numerical)
assert err < tol, err
def test_trapezoidal_conv_rate():
"""Check empirical convergence rates against the expected -2."""
from math import exp
f = lambda x: x**0.5
F = lambda x: (2.0/3)*x**(3.0/2)
a = 0.0 + 0.1; b = 4.0 # a adjusted by 0.1
r = convergence_rates(f, F, a, b, 14)
print r
tol = 0.01
assert abs(abs(r[-1]) - 2) < tol, r[-4:]
def convergence_rates(f, F, a, b, num_experiments=14):
from math import log
from numpy import zeros
exact = F(b) - F(a)
n = zeros(num_experiments, dtype=int)
E = zeros(num_experiments)
r = zeros(num_experiments-1)
for i in range(num_experiments):
n[i] = 2**(i+1)
numerical = trapezoidal(f, a, b, n[i])
E[i] = abs(exact - numerical)
if i > 0:
r_im1 = log(E[i]/E[i-1])/log(float(n[i])/n[i-1])
r[i-1] = float('%.2f' % r_im1) # Truncate to two decimals
return r
test_trapezoidal_one_exact_result()
test_trapezoidal_conv_rate()
Filename: test_trapezoidal3.py.
Remarks
The convergence rate test fails. Printing out r shows that the
actual convergence rate for this integral is \( -1.5 \) and not \( -2 \).
The reason is that the error in the trapezoidal method
is \( -(b-a)^3n^{-2}f''(\xi) \) for some (unknown) \( \xi\in [a,b] \).
With \( f(x)=\sqrt{x} \), \( f''(\xi)\rightarrow -\infty \) as \( \xi\rightarrow 0 \),
pointing to a potential problem in the size of the error.
Running a test with \( a>0 \), say \( \int_{0.1}^4\sqrt{x}dx \) shows that
the convergence rate is indeed restored to -2.
Exercise 37: Rectangle methods
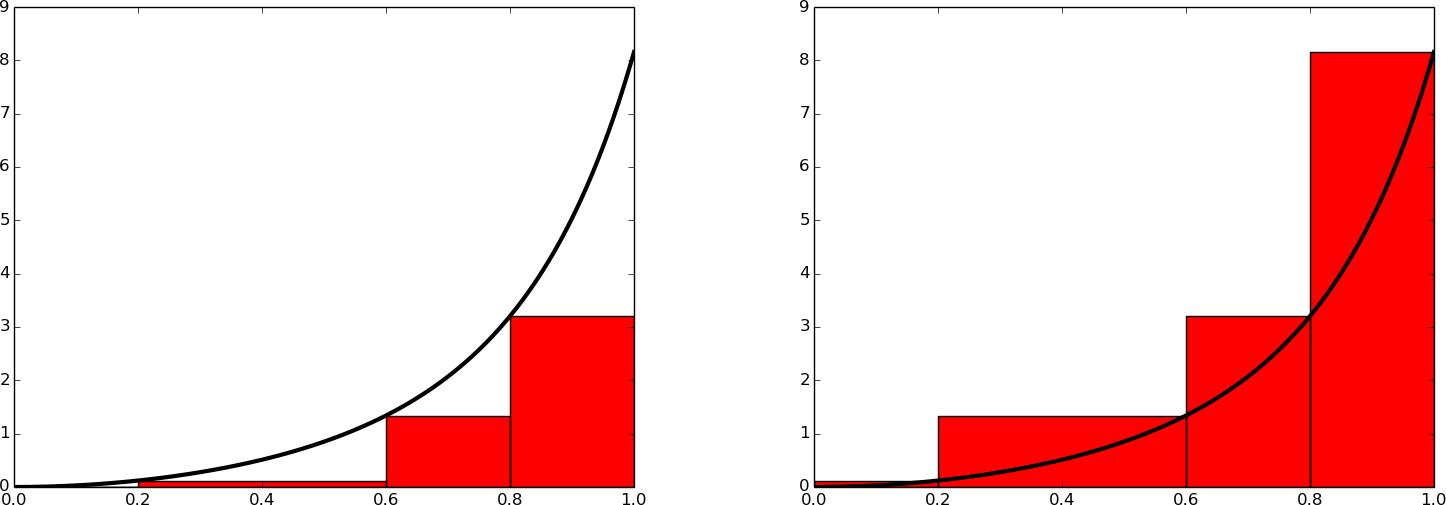
The midpoint method divides the interval of integration into equal-sized subintervals and approximates the integral in each subinterval by a rectangle whose height equals the function value at the midpoint of the subinterval. Instead, one might use either the left or right end of the subinterval as illustrated in Figure 13. This defines a rectangle method of integration. The height of the rectangle can be based on the left or right end or the midpoint.
Figure 13: Illustration of the rectangle method with evaluating the rectangle height by either the left or right point.
a)
Write a function rectangle(f, a, b, n, height='left') for
computing an integral \( \int_a^bf(x)dx \) by the rectangle method
with height computed based on the value of height, which is either
left, right, or mid.
Placing the code for both a and b into one file, the code may read:
def rectangle(f, a, b, n, height='left'):
"""Uses a rectangle method for integrating f. The height of
each rectangle is computed either at the left end, middle or
right end of each sub-interval"""
h = float(b-a)/n
if height == 'left':
start = a
elif height == 'mid':
start = a + h/2.0
else: # Must be right end
start = a + h
result = 0
for i in range(n):
result += f((start) + i*h)
result *= h
return result
def test_rectangle_one_exact_result():
"""Compare one hand-computed result."""
from math import exp
v = lambda t: 3*(t**2)*exp(t**3)
method = ['left', 'mid', 'right']
n = 2
exact = [0.4249306699000599, 1.3817914596908085, \
4.5023534125886275]
tol = 1E-14
for i in range(len(method)):
numerical = rectangle(v, 0, 1, n, method[i])
err = abs(exact[i] - numerical)
assert err < tol, err
def test_rectangle_linear():
"""Check that linear functions are integrated exactly
(with midpoint) or with a known correctable error (left
and right)"""
method = ['left', 'mid', 'right']
f = lambda x: 6*x - 4
slope = 6
F = lambda x: 3*x**2 - 4*x # Anti-derivative
# From the slope of f (i.e. 6), we know that left will
# under-estimate the inegral by C (given below), while
# right will over-estimate by C
a = 1.2; b = 4.4
exact = F(b) - F(a)
#tol = 1E-14
tol = 1E-13 # Slightly relaxed compared to previously
for n in 2, 20, 21:
h = float(b-a)/n
C = n*(0.5*slope*h**2) # Correction term for left/right
for i in range(len(method)):
numerical = rectangle(f, a, b, n, method[i])
if (method[i] == 'left'):
numerical += C
elif (method[i] == 'right'):
numerical -= C
err = abs(exact - numerical)
assert err < tol, 'n = %d, err = %g' % (n,err)
def test_rectangle_conv_rate():
"""Check empirical convergence rates against the expected rate,
which is -2 for midpoint and -1 for left and right."""
from math import exp
method = ['left', 'mid', 'right']
v = lambda t: 3*(t**2)*exp(t**3)
V = lambda t: exp(t**3)
a = 1.1; b = 1.9
tol = 0.01
for i in range(len(method)):
r = convergence_rates(v, V, a, b, method[i], 14)
print r
if (method[i] == 'left') or (method[i] == 'right'):
assert abs(abs(r[-1]) - 1) < tol, r[-4:]
else:
assert abs(abs(r[-1]) - 2) < tol, r[-4:]
def convergence_rates(f, F, a, b, height, num_experiments=14):
from math import log
from numpy import zeros
exact = F(b) - F(a)
n = zeros(num_experiments, dtype=int)
E = zeros(num_experiments)
r = zeros(num_experiments-1)
for i in range(num_experiments):
n[i] = 2**(i+1)
numerical = rectangle(f, a, b, n[i], height)
E[i] = abs(exact - numerical)
if i > 0:
r_im1 = log(E[i]/E[i-1])/log(float(n[i])/n[i-1])
r[i-1] = float('%.2f' % r_im1) # Truncate to two decimals
return r
test_rectangle_one_exact_result()
test_rectangle_linear()
test_rectangle_conv_rate()
b)
Write three test functions for the three unit test procedures
described in the section Proper test procedures. Make sure you
test for height equal to left, right, and mid. You may
call the midpoint function for checking the result when height=mid.
Edit test_trapezoidal.py.
See code above.
Filename: rectangle_methods.py.
Exercise 38: Adaptive integration
Suppose we want to use the trapezoidal or midpoint method to compute an integral \( \int_a^b f(x)dx \) with an error less than a prescribed tolerance \( \epsilon \). What is the appropriate size of \( n \)?
To answer this question, we may enter an iterative procedure where we compare the results produced by \( n \) and \( 2n \) intervals, and if the difference is smaller than \( \epsilon \), the value corresponding to \( 2n \) is returned. Otherwise, we halve \( n \) and repeat the procedure.
It may be a good idea to organize your code so that the function adaptive_integration can be used
easily in future programs you write.
a) Write a function
adaptive_integration(f, a, b, eps, method=midpoint)
that implements the idea above (eps corresponds to the tolerance
\( \epsilon \), and method can be midpoint or trapezoidal).
Easing the answers to the whole of this exercise, as well as preparing for easy use of adaptive integration in future programs, we organize the coding of tasks a, b and c into one file, making it a module. The code then reads:
from numpy import linspace, zeros, sqrt, log
from trapezoidal import trapezoidal
from midpoint import midpoint
def adaptive_integration(f, a, b, eps, method='midpoint'):
n_limit = 1000000 # Just a choice (used to avoid inf loop)
n = 2
if method == 'trapezoidal':
integral_n = trapezoidal(f, a, b, n)
integral_2n = trapezoidal(f, a, b, 2*n)
diff = abs(integral_2n - integral_n)
print 'trapezoidal diff: ', diff
while (diff > eps) and (n < n_limit):
integral_n = trapezoidal(f, a, b, n)
integral_2n = trapezoidal(f, a, b, 2*n)
diff = abs(integral_2n - integral_n)
print 'trapezoidal diff: ', diff
n *= 2
elif method == 'midpoint':
integral_n = midpoint(f, a, b, n)
integral_2n = midpoint(f, a, b, 2*n)
diff = abs(integral_2n - integral_n)
print 'midpoint diff: ', diff
while (diff > eps) and (n < n_limit):
integral_n = midpoint(f, a, b, n)
integral_2n = midpoint(f, a, b, 2*n)
diff = abs(integral_2n - integral_n)
print 'midpoint diff: ', diff
n *= 2
else:
print 'Error - adaptive integration called with unknown par'
# Now we check if acceptable n was found or not
if diff <= eps: # Success
print 'The integral computes to: ', integral_2n
return n
else:
return -n # Return negative n to tell "not found"
def application():
"""...Tasks b) and c)"""
def f(x):
return x**2
def g(x):
return sqrt(x)
#eps = 1E-1 # Just switch between these two eps values
eps = 1E-10
#a = 0.0
a = 0.0 + 0.01; # If we adjust a, sqrt(x) is handled easily
b = 2.0
# ...f
n = adaptive_integration(f, a, b, eps, 'midpoint')
if n > 0:
print 'Sufficient n is: %d' % (n)
else:
print 'No n was found in %d iterations' % (n_limit)
n = adaptive_integration(f, a, b, eps, 'trapezoidal')
if n > 0:
print 'Sufficient n is: %d' % (n)
else:
print 'No n was found in %d iterations' % (n_limit)
# ...g
n = adaptive_integration(g, a, b, eps, 'midpoint')
if n > 0:
print 'Sufficient n is: %d' % (n)
else:
print 'No n was found in %d iterations' % (n_limit)
n = adaptive_integration(g, a, b, eps, 'trapezoidal')
if n > 0:
print 'Sufficient n is: %d' % (n)
else:
print 'No n was found in %d iterations' % (n_limit)
# Task c, make plot for both midpoint and trapezoidal
eps = linspace(1E-1,10E-10,10)
n_m = zeros(len(eps))
n_t = zeros(len(eps))
for i in range(len(n_m)):
n_m[i] = adaptive_integration(g, a, b, eps[i], 'midpoint')
n_t[i] = adaptive_integration(g, a, b, eps[i], 'trapezoidal')
import matplotlib.pyplot as plt
plt.plot(log(eps),n_m,'b-',log(eps),n_t,'r-')
plt.xlabel('log(eps)')
plt.ylabel('n for midpoint (blue) and trapezoidal (red)')
plt.show()
print n
print eps
if __name__ == '__main__':
application()
b) Test the method on \( \int_0^2x^2dx \) and \( \int_0^2\sqrt{x}dx \) for \( \epsilon = 10^{-1}, 10^{-10} \) and write out the exact error.
See the code above. Note that, in our suggested code, it is foreseen
that the programmer switches between the two epsilon values by use of commenting, i.e.
adding/removing #. This may of course be avoided, if desirable, by asking the user for epsilon.
c) Make a plot of \( n \) versus \( \epsilon \in [10^{-1}, 10^{-10}] \) for \( \int_0^2\sqrt{x}dx \). Use logarithmic scale for \( \epsilon \).
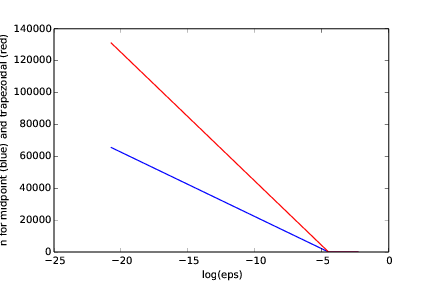
From Figure 14, we see that the stricter the value of epsilon, the larger the
difference between the midpoint and the trapezoidal methods. For a given value for epsilon, the
midpoint method comes within the tolerance with fewer intervals (lower value of n) than does
the trapezoidal method. This should be expected, since the midpoint method is somewhat more accurate
than the trapezoidal method.
Figure 14: Showing n as a function of log(eps) when \( \int_0^2\sqrt{x}dx \) is computed by the midpoint (blue) and the trapezoidal (red) method.
One way of producing this plot, is by using the code lines included at the end of
adaptive_integration.py (see the above).
Filename: adaptive_integration.py.
Remarks
The type of method explored in this exercise is called adaptive, because it tries to adapt the value of \( n \) to meet a given error criterion. The true error can very seldom be computed (since we do not know the exact answer to the computational problem), so one has to find other indicators of the error, such as the one here where the changes in the integral value, as the number of intervals is doubled, is taken to reflect the error.
Exercise 39: Integrating x raised to x
Consider the integral
$$ I = \int_0^4 x^x\,dx\thinspace .$$
The integrand \( x^x \) does not have an anti-derivative that can be expressed in terms of standard functions (visit http://wolframalpha.com and type
integral(x**x,x) to convince yourself that
our claim is right. Note that Wolfram alpha does give you an answer, but that answer is an approximation, it is not exact. This is because
Wolfram alpha too uses numerical methods to arrive at the answer, just as you will in this exercise). Therefore, we are forced to compute the integral by numerical methods. Compute a result that is right to four digits.
Use ideas from Exercise 38: Adaptive integration.
When the function adaptive_integration is available, the code may be written as:
from adaptive_integration import adaptive_integration
def f(x):
return x**x
eps = 1E-4
a = 0.0; b = 2.0
# Choose midpoint method
n = adaptive_integration(f, a, b, eps, 'midpoint')
if n > 0:
print 'Sufficient n is: %d' % (n)
else:
# The negative n is returned to signal that the upper limit of n
# was passed
print 'No n was found in %d iterations' % (abs(n))
Remember that adaptive_integration prints out the computed integral, so no effort
in that respect is required here.
Running the program, gives a printout to the screen showing how diff gets smaller and
smaller each time. The final two lines of the printout read:
The integral computes to: 2.83384395958
Sufficient n is: 256
The computed value may be compared to what Wolfram alpha gives. Remember that since we have not computed the exact error, we can not guarantee that the "result is right to four digits". However, we have reason to believe that we "are close". Typically, when it is known that the error measure used is not precise, the tolerance is made stricter.
Filename: integrate_x2x.py.
Exercise 40: Integrate products of sine functions
In this exercise we shall integrate $$ I_{j,k} = \int_{-\pi}^{\pi} \sin(jx)\sin(kx)dx,$$ where \( j \) and \( k \) are integers.
a) Plot \( \sin(x)\sin(2x) \) and \( \sin(2x)\sin(3x) \) for \( x\in ]-\pi,\pi] \) in separate plots. Explain why you expect \( \int_{-\pi}^{\pi}\sin x\sin 2x\,dx=0 \) and \( \int_{-\pi}^{\pi}\sin 2x\sin 3x\,dx=0 \).
b) Use the trapezoidal rule to compute \( I_{j,k} \) for \( j=1,\ldots,10 \) and \( k=1,\ldots,10 \).
Filename: products_sines.py.
Exercise 41: Revisit fit of sines to a function
This is a continuation of Exercise 28: Fit sines to straight line. The task is to approximate a given function \( f(t) \) on \( [-\pi,\pi] \) by a sum of sines, $$ \begin{equation} S_N(t) = \sum_{n=1}^{N} b_n \sin(nt)\thinspace . \tag{3.27} \end{equation} $$ We are now interested in computing the unknown coefficients \( b_n \) such that \( S_N(t) \) is in some sense the best approximation to \( f(t) \). One common way of doing this is to first set up a general expression for the approximation error, measured by "summing up" the squared deviation of \( S_N \) from \( f \): $$ E = \int_{-\pi}^{\pi}(S_N(t)-f(t))^2dt\thinspace .$$ We may view \( E \) as a function of \( b_1,\ldots,b_N \). Minimizing \( E \) with respect to \( b_1,\ldots,b_N \) will give us a best approximation, in the sense that we adjust \( b_1,\ldots,b_N \) such that \( S_N \) deviates as little as possible from \( f \).
Minimization of a function of \( N \) variables, \( E(b_1,\ldots,b_N) \) is mathematically performed by requiring all the partial derivatives to be zero: $$ \begin{align*} \frac{\partial E}{\partial b_1} & = 0,\\ \frac{\partial E}{\partial b_2} & = 0,\\ &\vdots\\ \frac{\partial E}{\partial b_N} & = 0\thinspace . \end{align*} $$
a) Compute the partial derivative \( \partial E/\partial b_1 \) and generalize to the arbitrary case \( \partial E/\partial b_n \), \( 1\leq n\leq N \).
We see that the partial derivative of \( E \) with respect to any one of the \( b \) coefficients will take on the same form, meaning that $$ \begin{equation*} \frac{\partial E}{\partial b_n} = 2\int_{-\pi}^{\pi} (S_N(t)-f(t))\sin(nt)dt, \nonumber \end{equation*} $$ where \( 1\leq n\leq N \).
b) Show that $$ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(t)\sin(nt)\,dt\thinspace .$$
Requiring $$ \begin{equation*} \frac{\partial E}{\partial b_n} = 0, \nonumber \end{equation*} $$ means that the following must apply, $$ \begin{equation*} 2\int_{-\pi}^{\pi} (S_N(t)-f(t))\sin(nt)dt = 0. \nonumber \end{equation*} $$ This may be rewritten as $$ \begin{equation*} \int_{-\pi}^{\pi} S_N(t)\sin(nt)dt = \int_{-\pi}^{\pi} f(t)\sin(nt)dt \nonumber \end{equation*} $$ or, if we insert the expression for \( S_N \), we get $$ \begin{equation*} \int_{-\pi}^{\pi} (\sum_{i=1}^{N} b_i \sin(it))\sin(nt)dt = \int_{-\pi}^{\pi} f(t)\sin(nt)dt, \nonumber \end{equation*} $$ where the summation variable in \( S_N \) has been changed from \( n \) to \( i \), avoiding conflict with the \( n \) already present in \( \sin(nt) \).
Now, since $$ \begin{equation*} \int_{-\pi}^{\pi} \sin^2(nt)dt = \pi, \nonumber \end{equation*} $$ while $$ \begin{equation*} \int_{-\pi}^{\pi} \sin(it)\sin(nt)dt = 0, \nonumber \end{equation*} $$ when \( i \neq n \), we arrive at $$ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(t)\sin(nt)\,dt\thinspace .$$
c)
Write a function integrate_coeffs(f, N, M) that computes \( b_1,\ldots,b_N \)
by numerical integration, using \( M \) intervals in the trapezoidal rule.
Answers to all (programming) questions in this exercise are collected in one script which reads:
from numpy import linspace, zeros, pi, sin, exp
from trapezoidal import trapezoidal
def integrate_coeffs(f, N, M):
b = zeros(N)
left_end = -pi; right_end = pi
for n in range(1, N+1):
f_sin = lambda t: f(t)*sin(n*t)
b[n-1] = (1/pi)*trapezoidal(f_sin, left_end, right_end, M)
return b
def test_integrate_coeffs():
"""Check that sin(nt) are integrated exactly by trapezoidal"""
def f(t):
return 1
tol = 1E-14
N = 10
M = 100
b = integrate_coeffs(f, N, M)
print b
for i in range(0, 10):
err = abs(b[i]) # Supposed to be zero
assert err < tol, 'n = %d, err = %g' % (n,err)
def plot_approx(f, N, M, filename):
def S_N(b,t):
sum = 0
for i in range(len(b)):
sum += b[i]*sin((i+1)*t)
return sum
left_end = -pi; right_end = pi
time = linspace(-pi, pi, 100)
y = f(time)
b = integrate_coeffs(f, N, M)
y_approx = S_N(b, time)
import matplotlib.pyplot as plt
plt.figure(); plt.plot(time, y, 'k-', time, y_approx, 'k--')
plt.xlabel('t'); plt.ylabel('f (solid) and S (dashed)')
plt.savefig(filename)
def application():
def f(t):
return (1/pi)*t
N = 3
M = 100
b = integrate_coeffs(f, N, M)
print b
for N in [3, 6, 12, 24]:
plot_filename = 'C:/Users/Svein/Desktop/S_whenNis' \
+ str(N) + '.pdf'
plot_approx(f, N, M, plot_filename)
def g(t):
return exp(-(t-pi))
plot_filename = 'C:/Users/Svein/Desktop/new_f_S_whenNis' \
+ str(100) + '.pdf'
plot_approx(g, 100, M, plot_filename)
if __name__ == '__main__':
application()
test_integrate_coeffs()
d)
A remarkable property of the trapezoidal rule is that it is exact for integrals
\( \int_{-\pi}^{\pi}\sin nt\,dt \) (when subintervals are of equal size). Use this
property to create a function test_integrate_coeff to verify the
implementation of integrate_coeffs.
See code given above.
e)
Implement the choice \( f(t) = \frac{1}{\pi}t \) as a Python function
f(t) and call integrate_coeffs(f, 3, 100) to see what the
optimal choice of \( b_1, b_2, b_3 \) is.
See code given above. Running the script produces a printout of the following values for the \( b \) coefficients:
0.63641032
-0.3178909
0.2115779
f)
Make a function plot_approx(f, N, M, filename) where you plot f(t)
together with the best approximation \( S_N \) as computed above,
using \( M \) intervals for numerical integration. Save the plot to a file
with name filename.
See code given above.
g)
Run plot_approx(f, N, M, filename) for \( f(t) = \frac{1}{\pi}t \)
for \( N=3,6,12,24 \). Observe how the approximation improves.
See code given above. Running the program will produce one plot (Figure 15, Figure 16, Figure 17 and Figure 18) for each value of \( N \). We see from the plots that the larger the \( N \), the better the approximation.
Figure 15: The function \( f(t) \) and its approximation \( S_N(t) \) when \( N = 3 \).
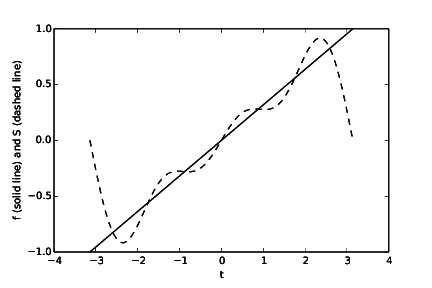
Figure 16: The function \( f(t) \) and its approximation \( S_N(t) \) when \( N = 6 \).
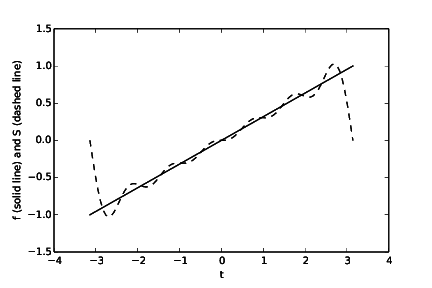
Figure 17: The function \( f(t) \) and its approximation \( S_N(t) \) when \( N = 12 \).

Figure 18: The function \( f(t) \) and its approximation \( S_N(t) \) when \( N = 24 \).

h)
Run plot_approx for \( f(t) = e^{-(t-\pi)} \) and \( N=100 \).
Observe a fundamental problem: regardless of \( N \), \( S_N(-\pi)=0 \), not
\( e^{2\pi}\approx 535 \). (There are ways to fix this issue.)
See code given above. Running the program (also) produces the plot seen in Figure 19. Clearly, the approximation is no good at the endpoints of the interval.
Figure 19: The new function \( f(t) \) and its approximation \( S_N(t) \) when \( N = 100 \).

Filename: autofit_sines.py.
Exercise 42: Derive the trapezoidal rule for a double integral
Use ideas in the section The midpoint rule for a double integral to derive a formula for computing a double integral \( \int_a^b\int_c^d f(x,y)dydx \) by the trapezoidal rule. Implement and test this rule.
We introduce a help function \( g(x) \) and write $$ \int_a^b \int_c^d f(x,y) dydx = \int_a^b g(x)dx,\quad g(x) = \int_c^d f(x,y) dy\thinspace .$$ Next, we apply the trapezoidal rule (The composite trapezoidal rule) to each of the integrals $$ \int_a^b g(x)dx,\quad g(x) = \int_c^d f(x,y) dy\thinspace .$$
Starting with \( g(x)=\int_c^d f(x,y)dy \), we introduce \( n_y \) intervals on \( [c,d] \) with length \( h_y \). The trapezoidal rule for this integral then becomes $$ g(x) = \int_c^d f(x,y) dy \approx h_y \left[\frac{1}{2}f(x,c) + \sum_{j=1}^{n_y-1}f(x,y_j) + \frac{1}{2}f(x,d) \right],$$ with \( y_j = c + jh_y \). For the outer integral \( \int_a^b g(x)dx \), we get: $$ \int_a^b g(x)dx \approx h_x \left[\frac{1}{2}g(a) + \sum_{i=1}^{n_x-1}g(x_i) + \frac{1}{2}g(b) \right], \quad x_i=a + ih_x\thinspace .$$ Combining the formulas, we get the composite trapezoidal method for a double integral: $$ \begin{align} \int_a^b \int_c^d f(x,y) dydx &\approx h_x \biggl[\frac{1}{2}\left(h_y \left[\frac{1}{2}f(a,c) + \sum_{j=1}^{n_y-1}f(a,y_j) + \frac{1}{2}f(a,d) \right]\right) + \nonumber\\ &\quad \sum_{i=1}^{n_x-1}\left(h_y \left[\frac{1}{2}f(x_i,c) + \sum_{j=1}^{n_y-1}f(x_i,y_j) + \frac{1}{2}f(x_i,d) \right]\right)+\nonumber\\ &\quad \frac{1}{2}\left(h_y \left[\frac{1}{2}f(b,c) + \sum_{j=1}^{n_y-1}f(b,y_j) + \frac{1}{2}f(b,d) \right]\right) \biggr]\nonumber\\ &= h_xh_y \biggl[\frac{1}{4}\left(f(a,c) + f(a,d) + f(b,c) + f(b,d) \right) +\nonumber\\ &\quad \frac{1}{2}\sum_{i=1}^{n_x-1}\left(f(a + ih_x,c) + f(a + ih_x,d)\right) + \nonumber\\ &\quad \frac{1}{2}\sum_{j=1}^{n_y-1}\left(f(a,c + jh_y) + f(b,c + jh_y)\right) + \nonumber\\ &\quad \sum_{i=1}^{n_x-1} \sum_{j=1}^{n_y-1} f(a + ih_x, c + jh_y)\biggr]\thinspace . \nonumber \end{align} $$
The formula may be implemented and tested as shown in trapezoidal_double.py:
def trapezoidal_double(f, a, b, c, d, nx, ny):
hx = (b - a)/float(nx)
hy = (d - c)/float(ny)
I = 0.25*(f(a, c) + f(a, d) + f(b, c) + f(b, d))
Ix = 0
for i in range(1, nx):
xi = a + i*hx
Ix += f(xi, c) + f(xi, d)
I += 0.5*Ix
Iy = 0
for j in range(1, ny):
yj = c + j*hy
Iy += f(a, yj) + f(b, yj)
I += 0.5*Iy
Ixy = 0
for i in range(1, nx):
for j in range(1, ny):
xi = a + i*hx
yj = c + j*hy
Ixy += f(xi, yj)
I += Ixy
I *= hx*hy
return I
def test_trapezoidal_double():
"""Test that a linear function is integrated exactly."""
def f(x, y):
return 2*x + y
a = 0; b = 2; c = 2; d = 3
import sympy
x, y = sympy.symbols('x y')
I_expected = sympy.integrate(f(x, y), (x, a, b), (y, c, d))
# Test three cases: nx < ny, nx = ny, nx > ny
for nx, ny in (3, 5), (4, 4), (5, 3):
I_computed = trapezoidal_double(f, a, b, c, d, nx, ny)
tol = 1E-14
#print I_expected, I_computed
assert abs(I_computed - I_expected) < tol
if __name__ == '__main__':
test_trapezoidal_double()
Filename: trapezoidal_double.py.
Exercise 43: Compute the area of a triangle by Monte Carlo integration
Use the Monte Carlo method from the section Monte Carlo integration for complex-shaped domains to compute the area of a triangle with vertices at \( (-1,0) \), \( (1,0) \), and \( (3,0) \).
The program MC_triangle.py may be written as:
from MC_double import MonteCarlo_double
def g(x, y):
"""Utilize that triangle is symmetric about y-axis """
return (1 if (0 <= y <= -3*abs(x) + 3) else -1 )
print MonteCarlo_double(lambda x, y: 1, g, -1, 1, 0, 3, 1000)
Filename: MC_triangle.py.