Exercises

Exercise 72: Understand why Newton's method can fail

The purpose of this exercise is to understand when Newton's method works and fails. To this end, solve $ \tanh x=0 $ by Newton's method and study the intermediate details of the algorithm. Start with $ x_0=1.08 $. Plot the tangent in each iteration of Newton's method. Then repeat the calculations and the plotting when $ x_0=1.09 $. Explain what you observe.

Solution.

The program may be written as:

function [solution, no_iterations] =...
                                Newton_failure(f, dfdx, x0, eps)
    x = x0;
    f_value = f(x);
    iteration_counter = 0;
    while abs(f_value) > eps && iteration_counter < 100
        try
            fprintf('Current x vaule: %g \n', x);
            plot_line(f, x, f_value, dfdx(x));
            x = x - (f_value)/dfdx(x);
        catch
            fprintf('Error! - derivative zero for x = \n', x)
            exit(1)
        end
        f_value = f(x);
        iteration_counter = iteration_counter + 1;
    end
    % Here, either a solution is found, or too many iterations
    if abs(f_value) > eps
        iteration_counter = -1;
    end
    solution = x;
    no_iterations = iteration_counter;
end

which may be called from the script use_my_Newton_failure.m:

f = @(x) tanh(x);
dfdx = @(x) 1 - tanh(x)^2;

[solution, no_iterations] = Newton_failure(f, dfdx, 1.08, 0.001)

if no_iterations > 0      % Solution found
    fprintf('Number of function calls: %d \n', 1 + 2*no_iterations); 
    fprintf('A solution is: %f \n', solution);
else
    fprintf('Solution not found! \n');
end

Note that Newton_failure.m calls the function plot_line (located in plot_line.m), reading:

function plot_line(f, xn, f_xn, slope)
    % Plot both f(x) and the tangent or secant
    x_f = linspace(-2, 2, 100);
    y_f = f(x_f);
    x_t = linspace(xn-2, xn+2, 10);
    y_t = slope*x_t + (f_xn - slope*xn); % Straight line: ax + b
    figure(); 
    plot(x_t, y_t, 'r-', x_f, y_f, 'b-');   grid('on');
    xlabel('x'); ylabel('f(x)');
    disp('...press enter to continue')
    pause on; pause;
end

(The function plot_line is placed as a separate m-file so that it may be used also by the function secant_failure, which is to be written in another exercise.)

Running the program with x set to $ 1.08 $ produces a series of plots (and prints) showing the graph and the tangent for the present value of x. There are quite many plots, so we do not show them here. However, the tangent line "jumps" around a few times before it settles. In the final plot the tangent line goes through the solution at $ x = 0 $. The final printout brings the information:

Number of function calls: 13
A solution is: 0.000024

When we run the program anew, this time with x set to $ 1.09 $, we get another series of plots (and prints), but this time the tangent moves away from the (known) solution. The final printout we get states that:

Number of function calls: 19
A solution is: nan

Here, nan stands for "not a number", meaning that we got no solution value for x. That is, Newton's method diverged.

Filename: Newton_failure.*.

Exercise 73: See if the secant method fails

Does the secant method behave better than Newton's method in the problem described in Exercise 72: Understand why Newton's method can fail? Try the initial guesses

$ x_0=1.08 $ and $ x_1=1.09 $
$ x_0=1.09 $ and $ x_1=1.1 $
$ x_0=1 $ and $ x_1=2.3 $
$ x_0=1 $ and $ x_1=2.4 $

Solution.

The program may be written as:

% This file is not yet written.

which may be called from the script use_my_secant_failure.m:

f = @(x) tanh(x);
dfdx = @(x) 1 - tanh(x)^2;

% Requested trials:
%x0 = 1.08 , x1 = 1.09
%x0 = 1.09 , x1 = 1.1
%x0 = 1 , x1 = 2.3
%x0 = 1 , x1 = 2.4
[solution, no_iterations] = Secant_failure(f, 1, 2.4, 0.001)

if no_iterations > 0       % Solution found
    fprintf('Number of function calls: %d \n', 1 + 2*no_iterations); 
    fprintf('A solution is: %f \n', solution);
else
    fprintf('Solution not found! \n');
end

Note that, as with Newton_failure.m, the script plot_line.m is called for plotting each tangent.

The script converges with the three first-mentioned alternatives for $ x_0 $ and $ x_1 $. With the final set of parameter values, the method diverges with a printout:

Error! - denominator zero for x = 360.600893792

and a few more lines stating that an exception error has occurred.

Filename: secant_failure.*.

Exercise 74: Understand why the bisection method cannot fail

Solve the same problem as in Exercise 72: Understand why Newton's method can fail, using the bisection method, but let the initial interval be $ [-5,3] $. Report how the interval containing the solution evolves during the iterations.

Solution.

The code may be written as:

function [result1, result2] = ...
                           bisection_nonfailure(f, x_L, x_R, eps)
    if f(x_L)*f(x_R) > 0
       fprintf('Error! Function does not have opposite \n');
       fprintf('signs at interval endpoints!');
       exit(1); 
    end
    x_M = (x_L + x_R)/2;
    f_M = f(x_M);
    iteration_counter = 1;
    while abs(f_M) > eps
        left_f = f(x_L);
        right_f = f(x_R);
        if left_f*f_M > 0            % i.e., same sign
            x_L = x_M;
        else
            x_R = x_M;
        end
        fprintf('interval: [%f, %f]\n', x_L, x_R); 
        x_M = (x_L + x_R)/2;
        f_M = f(x_M);
        iteration_counter = iteration_counter + 1;
    end
    result1 = x_M;
    result2 = iteration_counter;
end

which may be called from the script use_my_bisection_nonfailure.m:

f = @(x) tanh(x);

a = -5; b = 3;

[solution, no_iterations] =...
                   bisection_nonfailure(f, a, b, 1.0e-6);

fprintf('Number of function calls: %d\n',1 + 2*no_iterations);
fprintf('A solution is: %f\n', solution);

Running the program produces the following printout:

interval: [-1.000000, 3.000000]
interval: [-1.000000, 1.000000]
Number of function calls: 7
A solution is: 0.000000

Filename: bisection_nonfailure.*.

Exercise 75: Combine the bisection method with Newton's method

An attractive idea is to combine the reliability of the bisection method with the speed of Newton's method. Such a combination is implemented by running the bisection method until we have a narrow interval, and then switch to Newton's method for speed.

Write a function that implements this idea. Start with an interval $ [a,b] $ and switch to Newton's method when the current interval in the bisection method is a fraction $ s $ of the initial interval (i.e., when the interval has length $ s(b-a) $). Potential divergence of Newton's method is still an issue, so if the approximate root jumps out of the narrowed interval (where the solution is known to lie), one can switch back to the bisection method. The value of $ s $ must be given as an argument to the function, but it may have a default value of 0.1.

Try the new method on $ \tanh(x)=0 $ with an initial interval $ [-10,15] $.

Solution.

The code may be written as:

function [solution, no_iterations] = ...
                      bisection_Newton(f, dfdx, x_L, x_R, eps, s)
    f_L = f(x_L);
    if f_L*f(x_R) > 0
        fprintf('Error! Function does not have opposite');
        fprintf('signs at interval endpoints!');
        exit(1);
    end
    x_M = (x_L + x_R)/2;
    f_M = f(x_M);
    iteration_counter = 1;
    interval_Newton = s*(x_R - x_L);  % Limit for swith to Newton
    while (x_R - x_L) > interval_Newton
        if f_L*f_M > 0    % i.e., same sign
            x_L = x_M;
            f_L = f_M;
        else
            x_R = x_M;
        end
        x_M = (x_L + x_R)/2;
        f_M = f(x_M);
        iteration_counter = iteration_counter + 1;
    end
    [x, no_iter] = Newton(f, dfdx, x_M, eps);
    solution = x;
    no_iterations = iteration_counter + no_iter;
end

which may be called from the script use_my_bisection_Newton.m:

f = @(x) tanh(x);
dfdx = @(x) 1 - tanh(x)^2; 

eps = 1e-6;
a = -10; b = 15;
s = 0.1;
[solution, no_iterations] =...
                        bisection_Newton(f, dfdx, a, b, eps, s);
fprintf('A solution x = %f was reached in %d iterations \n',...
                                       solution, no_iterations);

Running the program produces the following printout:

A solution x = 0.000000 was reached in 7 iterations

Filename: bisection_Newton.m.

Exercise 76: Write a test function for Newton's method

The purpose of this function is to verify the implementation of Newton's method in the Newton function in the file Newton.m Construct an algebraic equation and perform two iterations of Newton's method by hand. Find the corresponding size of $ |f(x)| $ and use this as value for eps when calling Newton. The function should then also perform two iterations and return the same approximation to the root as you calculated manually. Implement this idea for a unit test as a test function test_Newton().

Solution.

Here is the complete module with the test function.

function test_Newton()
    f = @(x) cos(x) + sin(x);
    dfdx = @(x) cos(x) - sin(x);
    x0 = 2;                     % initial guess
    %% Run two iterations with Newton's method
    x1 = x0 - f(x0)/dfdx(x0);
    x2 = x1 - f(x1)/dfdx(x1);
    x_expected = zeros(2,1);
    x_expected(1) = x1;  x_expected(2) = x2;
    eps = f(x_expected(length(x_expected)));  % this eps gives two iterations

    [x_computed, it_counter] = Newton_solver(f, dfdx, x0, eps, true);
    assert(it_counter == 2);
    tol = 1E-15;
    assert(abs(x_computed(1) - x_expected(1)) < tol);
    assert(abs(x_computed(2) - x_expected(2)) < tol);
end

Filename: test_Newton.m.

Exercise 77: Solve nonlinear equation for a vibrating beam

An important engineering problem that arises in a lot of applications is the vibrations of a clamped beam where the other end is free. This problem can be analyzed analytically, but the calculations boil down to solving the following nonlinear algebraic equation: $$ \cosh\beta \cos\beta = -1,$$ where $ \beta $ is related to important beam parameters through $$ \beta^4 = \omega^2 \frac{\varrho A}{EI},$$ where $ \varrho $ is the density of the beam, $ A $ is the area of the cross section, $ E $ is Young's modulus, and $ I $ is the moment of the inertia of the cross section. The most important parameter of interest is $ \omega $, which is the frequency of the beam. We want to compute the frequencies of a vibrating steel beam with a rectangular cross section having width $ b=25 $ mm and height $ h=8 $ mm. The density of steel is $ 7850 \mbox{ kg/m}^3 $, and $ E= 2\cdot 10^{11} $ Pa. The moment of inertia of a rectangular cross section is $ I=bh^3/12 $.

a) Plot the equation to be solved so that one can inspect where the zero crossings occur.

Hint.

When writing the equation as $ f(\beta)=0 $, the $ f $ function increases its amplitude dramatically with $ \beta $. It is therefore wise to look at an equation with damped amplitude, $ g(\beta) = e^{-\beta}f(\beta) = 0 $. Plot $ g $ instead.

Solution.

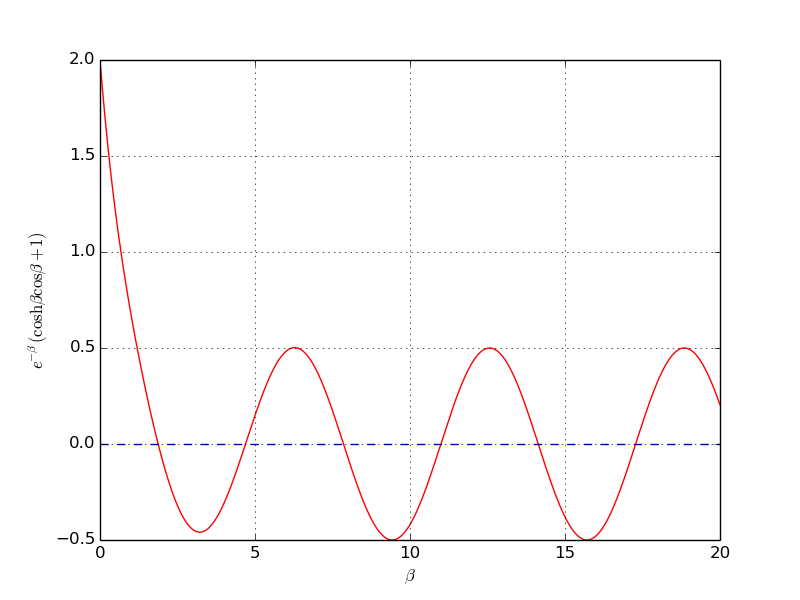
b) Compute the first three frequencies.

Solution.

Here is a complete program, using the Bisection method for root finding, based on intervals found from the plot above.

function beam_vib()

    plot_f()

    f_handle = @f;
    % Set up suitable intervals
    intervals = [1 3; 4 6; 7 9];
    betas = [];  % roots
    for i = 1:length(intervals) 
        beta_L = intervals(i, 1);  beta_R = intervals(i, 2);
        [beta, it] = bisection(f_handle, beta_L, beta_R, eps=1E-6);
        betas = [betas beta];
        f(beta)   
    end
    betas

    % Find corresponding frequencies

    function value = omega(beta, rho, A, E, I)
        value = sqrt(beta^4/(rho*A/(E*I)));
    end

    rho = 7850;  % kg/m^3
    E = 1.0E+11; % Pa
    b = 0.025;   % m
    h = 0.008;   % m
    A = b*h;
    I = b*h^3/12;

    for i = 1:length(betas)
        omega(betas(i), rho, A, E, I)
    end

end

function value = f(beta)
    value = cosh(beta).*cos(beta) + 1;
end

function value = damped(beta)
    % Damp the amplitude of f. It grows like cosh, i.e. exp.
    value = exp(-beta).*f(beta);
end

function plot_f()
    beta = linspace(0, 20, 501);
    %y = f(x)
    y = damped(beta);
    plot(beta, y, 'r', [beta(1), beta(length(beta))], [1, 1], 'b--')
    grid('on');
    xlabel('beta');
    ylabel('exp(-beta) (cosh(beta) cos(beta) +1)')
    savefig('tmp1.png'); savefig('tmp1.pdf')
end

The output of $ \beta $ reads $ 1.875 $, $ 4.494 $, $ 7.855 $, and corresponding $ \omega $ values are $ 29 $, $ 182 $, and $ 509 $ Hz.

Filename: beam_vib.m.