The FEniCS programs we have written so far have been designed as flat Python scripts. This works well for solving simple demo problems. However, when you build a solver for an advanced application, you will quickly find the need for more structured programming. In particular, you may want to reuse your solver to solve a large number of problems where you vary the boundary conditions, the domain, and coefficients such as material parameters. In this chapter, we will see how to write general solver functions to improve the usability of FEniCS programs. We will also discuss how to utilize iterative solvers with preconditioners for solving linear systems and how to compute derived quantities, such as, e.g., the flux on a part of the boundary.

Refactoring the Poisson solver

All programs created in this book so far are "flat"; that is, they are not organized into logical, reusable units in terms of Python functions. Such flat programs are useful for quickly testing out some software, but not well suited for serious problem solving. We shall therefore look at how to refactor the Poisson solver from the chapter Fundamentals: Solving the Poisson equation. For a start, this means splitting the code into functions, but this is just a reordering of the existing statements. During refactoring, we also try make the functions we create as reusable as possible in other contexts. We will also encapsulate statements specific to a certain problem into (non-reusable) functions. Being able to distinguish reusable code from specialized code is a key issue when refactoring code, and this ability depends on a good mathematical understanding of the problem at hand (what is general, what is special?). In a flat program, general and specialized code (and mathematics) are often mixed together, which tends to give a blurred understanding of the problem at hand.

A more general solver function

We consider the flat program developed in the section FEniCS implementation. Some of the code in this program is needed to solve any Poisson problem \( -\nabla^2 u=f \) on \( [0,1]\times [0,1] \) with \( u=\ub \) on the boundary, while other statements arise from our simple test problem. Let us collect the general, reusable code in a function called solver. Our special test problem will then just be an application of solver with some additional statements. We limit the solver function to just compute the numerical solution. Plotting and comparing the solution with the exact solution are considered to be problem-specific activities to be performed elsewhere.

We parameterize solver by \( f \), \( \ub \), and the resolution of the mesh. Since it is so trivial to use higher-order finite element functions by changing the third argument to FunctionSpace, we also add the polynomial degree of the finite element function space as an argument to solver.

from fenics import *

def solver(f, u_D, Nx, Ny, degree=1):
    """
    Solve -Laplace(u) = f on [0,1] x [0,1] with 2*Nx*Ny Lagrange
    elements of specified degree and u=u_D (Expresssion) on
    the boundary.
    """

    # Create mesh and define function space
    mesh = UnitSquareMesh(Nx, Ny)
    V = FunctionSpace(mesh, 'P', degree)

    def boundary(x, on_boundary):
        return on_boundary

    bc = DirichletBC(V, u_D, boundary)

    # Define variational problem
    u = TrialFunction(V)
    v = TestFunction(V)
    a = dot(grad(u), grad(v))*dx
    L = f*v*dx

    # Compute solution
    u = Function(V)
    solve(a == L, u, bc)

    return u

The remaining tasks of our initial program, such as calling the solve function with problem-specific parameters and plotting, can be placed in a separate function. Here we choose to put this code in a function named run_solver:

def run_solver():
    "Run solver to compute and post-process solution"

    # Set up problem parameters and call solver
    u_D = Expression('1 + x[0]*x[0] + 2*x[1]*x[1]')
    f = Constant(-6.0)
    u = solver(f, u_D, 6, 4, 1)

    # Plot solution
    u.rename('u', 'u')
    plot(u)

    # Save solution to file in VTK format
    vtkfile = File('poisson.pvd')
    vtkfile << u

The solution can now be computed, plotted, and saved to file by simply calling the run_solver function.

Writing the solver as a Python module

The refactored code is put in a file ft13_poisson_solver.py. We should make sure that such a file can be imported (and hence reused) in other programs. This means that all statements in the main program that are not inside functions should appear within a test if __name__ == '__main__':. This test is true if the file is executed as a program, but false if the file is imported. If we want to run this file in the same way as we can run ft13_poisson_solver.py, the main program is simply a call to run_solver() followed by a call interactive() to hold the plot:

if __name__ == '__main__':
    run_solver()
    interactive()

The complete code can be found in the file ft13_poisson_solver.py.

Verification and unit tests

The remaining part of our first program is to compare the numerical and the exact solutions. Every time we edit the code we must rerun the test and examine that max_error is sufficiently small so we know that the code still works. To this end, we shall adopt unit testing, meaning that we create a mathematical test and corresponding software that can run all our tests automatically and check that all tests pass. Python has several tools for unit testing. Two very popular ones are pytest and nose. These are almost identical and very easy to use. More classical unit testing with test classes is offered by the built-in module unittest, but here we are going to use pytest (or nose) since that will result in shorter and clearer code.

Mathematically, our unit test is that the finite element solution of our problem when \( f=-6 \) equals the exact solution \( u=\ub=1+x^2+2y^2 \) at the vertices of the mesh. We have already created a code that finds the error at the vertices for our numerical solution. Because of rounding errors, we cannot demand this error to be zero, but we have to use a tolerance, which depends to the number of elements and the degrees of the polynomials in the finite element basis functions. If we want to test that the solver function works for meshes up to \( 2\times(20\times 20) \) elements and cubic Lagrange elements, \( 10^{-10} \) is an appropriate tolerance for testing that the maximum error vanishes (see the section Dissection of the program).

To make our test case work together with pytest and nose, we have to make a couple of small adjustments to our program. The simple rule is that each test must be placed in a function that

• has a name starting with test_,
• has no arguments, and
• implements a test expressed as assert success, msg.

A proper test function for implementing this unit test in the pytest or nose testing frameworks has the following form. Note that we perform the test for different mesh resolutions and degrees of finite elements.

def test_solver():
    "Test solver by reproducing u = 1 + x^2 + 2y^2"

    # Set up parameters for testing
    tol = 1E-10
    u_D = Expression('1 + x[0]*x[0] + 2*x[1]*x[1]')
    f = Constant(-6.0)

    # Iterate over mesh sizes and degrees
    for Nx, Ny in [(3, 3), (3, 5), (5, 3), (20, 20)]:
        for degree in 1, 2, 3:
            print('Solving on a 2 x (%d x %d) mesh with P%d elements.'
                  % (Nx, Ny, degree))

            # Compute solution
            u = solver(f, u_D, Nx, Ny, degree)

            # Extract the mesh
            mesh = u.function_space().mesh()

            # Compute maximum error at vertices
            vertex_values_u_D = u_D.compute_vertex_values(mesh)
            vertex_values_u  = u.compute_vertex_values(mesh)
            import numpy as np
            error_max = np.max(np.abs(vertex_values_u_D - \ 
                                      vertex_values_u))

            # Check maximum error
            msg = 'error_max = %g' % error_max
            assert error_max < tol, msg

if __name__ == '__main__':
    run_solver()
    interactive()

To run the test, we type the following command:

Terminal> py.test ft13_poisson_solver.py

This will run all functions test_*() (currently only the test_solver function) found in the file and report the results. For more verbose output, add the flags -s -v.

We shall make it a habit in the following test to encapsulate numerical test problems in unit tests as done above, and we strongly encourage the reader to create similar unit tests whenever a FEniCS solver is implemented.

Parameterizing the number of space dimensions

FEniCS makes it is easy to write a unified simulation code that can operate in 1D, 2D, and 3D. We will conveniently make use of this feature in forthcoming examples. As an appetizer, go back to the introductory programs ft01_poisson.py or ft13_poisson_solver.py and change the mesh construction from UnitSquareMesh(16, 16) to UnitCubeMesh(16, 16, 16). Now the domain is the unit cube partitioned into \( 16\times 16\times16 \) boxes, and each box is divided into six tetrahedron-shaped finite elements for computations. Run the program and observe that we can solve a 3D problem without any other modifications (!). The visualization allows you to rotate the cube and observe the function values as colors on the boundary.

If we want to parameterize the creation of unit interval, unit square, or unit cube over dimension, we can do so by encapsulating this part of the code in a function. Given a list or tuple with the divisions into cells in the various spatial coordinates, the following function returns the mesh for a \( d \)-dimensional cube:

def UnitHyperCube(divisions):
    mesh_classes = [UnitIntervalMesh, UnitSquareMesh, UnitCubeMesh]
    d = len(divisions)
    mesh = mesh_classes[d-1](*divisions)
    return mesh

The construction mesh_class[d-1] will pick the right name of the object used to define the domain and generate the mesh. Moreover, the argument *divisions sends all the components of the list divisions as separate arguments to the constructor of the mesh construction class picked out by mesh_class[d-1]. For example, in a 2D problem where divisions has two elements, the statement

mesh = mesh_classes[d-1](*divisions)

is equivalent to

mesh = UnitSquareMesh(divisions[0], divisions[1])

The solver function from ft13_poisson_solver.py may be modified to solve \( d \)-dimensional problems by replacing the Nx and Ny parameters by divisions, and calling the function UnitHyperCube to create the mesh. Note that UnitHyperCube is a function and not a class, but we have named it with CamelCase to make it look like a class:

mesh = UnitHyperCube(divisions)

Exercise 4: Solve a Poisson problem

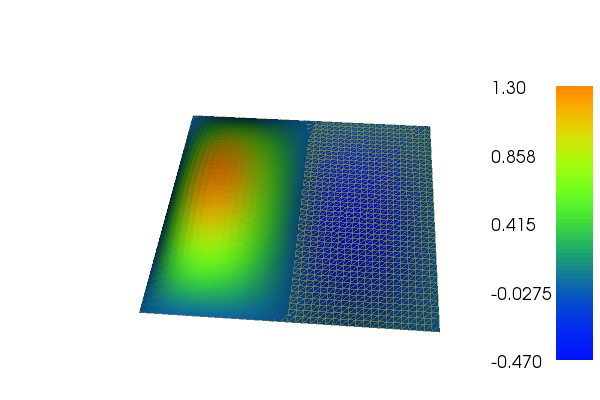
Solve the following problem $$ \begin{align} \nabla^2 u &= 2e^{-2x}\sin(\pi y)((4-5\pi^2)\sin(2\pi x) - 8\pi\cos(2\pi x)) \hbox{ in }\Omega = [0,1]\times [0,1] \tag{5.1}\\ u &= 0\quad\hbox{ on }\partial\Omega \tag{5.2} \end{align} $$ The exact solution is given by $$ u(x,y) = 2e^{-2x}\sin(\pi x)\sin(\pi y)\tp$$ Compute the maximum numerical approximation error in a mesh with \( 2(N_x\times N_y) \) elements and in a mesh with double resolution: \( 4(N_x\times N_y) \) elements. Show that the doubling the resolution reduces the error by a factor 4 when using Lagrange elements of degree one. Make an illustrative plot of the solution too.

a) Base your implementation on editing the program ft01_poisson.py.

Hint 1.

Hint 2.

Filename: poisson_fsin_flat.

Solution.

from fenics import *

Nx = Ny = 20
error = []
for i in range(2):
    Nx *= (i+1)
    Ny *= (i+1)

    # Create mesh and define function space
    mesh = UnitSquareMesh(Nx, Ny)
    V = FunctionSpace(mesh, 'Lagrange', 1)

    # Define boundary conditions
    u0 = Constant(0)

    def u0_boundary(x, on_boundary):
        return on_boundary

    bc = DirichletBC(V, u0, u0_boundary)

    # Define variational problem
    u = TrialFunction(V)
    v = TestFunction(V)
    f = Expression('-2*exp(-2*x[0])*sin(pi*x[1])*('
                   '(4-5*pow(pi,2))*sin(2*pi*x[0]) '
                   ' - 8*pi*cos(2*pi*x[0]))')
    # Note: no need for pi=DOLFIN_PI in f, pi is valid variable
    a = inner(nabla_grad(u), nabla_grad(v))*dx
    L = f*v*dx

    # Compute solution
    u = Function(V)
    solve(a == L, u, bc)

    u_e = Expression(
        '2*exp(-2*x[0])*sin(2*pi*x[0])*sin(pi*x[1])')

    u_e_Function = interpolate(u_e, V)         # exact solution
    u_e_array = u_e_Function.vector().array()  # dof values
    max_error = (u_e_array - u.vector().array()).max()
    print('max error:', max_error, '%dx%d mesh' % (Nx, Ny))
    error.append(max_error)

print('Error reduction:', error[1]/error[0])

# Plot solution and mesh
plot(u)

# Dump solution to file in VTK format
file = File("poisson.pvd")
file << u

# Hold plot
interactive()

b) Base your implementation on a new file that imports functionality from the module ft13_poisson_solver.py. Embed the check of the reduction of the numerical approximation error in a unit test. Filename: poisson_fsin_func.

Solution.

from poisson_solver import (
    solver, Expression, Constant, interpolate, File, plot,
    interactive)

def data():
    """Return data for this Poisson problem."""
    u0 = Constant(0)
    u_e = Expression(
        '2*exp(-2*x[0])*sin(2*pi*x[0])*sin(pi*x[1])')
    f = Expression('-2*exp(-2*x[0])*sin(pi*x[1])*('
                   '(4-5*pow(pi,2))*sin(2*pi*x[0]) '
                   ' - 8*pi*cos(2*pi*x[0]))')
    return u0, f, u_e

def test_solver():
    """Check convergence rate of solver."""
    u0, f, u_e = data()
    Nx = 20
    Ny = Nx
    error = []
    # Loop over refined meshes
    for i in range(2):
        Nx *= i+1
        Ny *= i+1
        print('solving on 2(%dx%d) mesh' % (Nx, Ny))
        u = solver(f, u0, Nx, Ny, degree=1)
        # Make a finite element function of the exact u_e
        V = u.function_space()
        u_e_array = interpolate(u_e, V).vector().array()
        max_error = (u_e_array - u.vector().array()).max()  # Linf norm
        error.append(max_error)
        print('max error:', max_error)
    for i in range(1, len(error)):
        error_reduction = error[i]/error[i-1]
        print('error reduction:', error_reduction)
        assert abs(error_reduction - 0.25) < 0.1

def application():
    """Plot the solution."""
    u0, f, u_e = data()
    Nx = 40
    Ny = Nx
    u = solver(f, u0, Nx, Ny, 1)
    # Dump solution to file in VTK format
    file = File("poisson.pvd")
    file << u
    # Plot solution and mesh
    plot(u)

if __name__ == '__main__':
    test_solver()
    application()
    # Hold plot
    interactive()

Remarks

This exercise demonstrates that changing a flat program to solve a new problem requires careful editing of statements scattered around in the file, while the solution in b), based on the solver function, requires no modifications of the ft13_poisson_solver.py file, just minimalistic additional new code in a separate file. The Poisson solver remains in one place (ft13_poisson_solver.py) while in a) we got two Poisson solvers. If you decide to switch to an iterative solution method for linear systems, you can do so in one place in b), and all applications can take advantage of the extension. Hopefully, with this exercise you realize that embedding PDE solvers in functions (or classes) makes more reusable software than flat programs.

Exercise 5: Refactor the code for membrane deflection

The ft14_membrane.py program simulates the deflection of a membrane. Refactor this code such that we have a solver function as in the program with name ft13_poisson_solver.py. Let the user have the option to choose a direct or iterative solver for the linear system. Also implement a unit test where you have \( p=4 \) (constant) and use P2 and P3 elements. In this case, the exact solution is quadratic in \( x \) and \( y \) and will be "exactly" reproduced by P2 and higher-order elements.

Solution.

def solver(
    f, u_b, mesh, degree=1,
    linear_solver='Krylov', # Alt: 'direct'
    ...):
    V = FunctionSpace(mesh, 'P', degree)
    # code as before

def application(beta, R0, num_elements_radial_dir):
    # Scaled pressure function
    p = Expression(
        '4*exp(-pow(beta,2)*(pow(x[0], 2) + pow(x[1]-R0, 2)))',
        beta=beta, R0=R0)

    # Generate mesh over the unit circle
    domain = Circle(Point(0.0, 0.0), 1.0)
    mesh = generate_mesh(domain, num_elements_radial_dir)

    w = solver(p, Constant(0), mesh, degree=1,
               linear_solver='direct')
    w.rename('w', 'deflection')  # set name and label (description)

    # Plot scaled solution, mesh and pressure
    plot(mesh, title='Mesh over scaled domain')
    plot(w, title='Scaled ' + w.label())
    V = w.function_space()
    p = interpolate(p, V)
    p.rename('p', 'pressure')
    plot(p, title='Scaled ' + p.label())

    # Dump p and w to file in VTK format
    vtkfile1 = File('membrane_deflection.pvd')
    vtkfile1 << w
    vtkfile2 = File('membrane_load.pvd')
    vtkfile2 << p

def test_membrane():
    """Verification for constant pressure."""
    p = Constant(4)
    # Generate mesh over the unit circle
    domain = Circle(Point(0.0, 0.0), 1.0)
    for degree in 2, 3:
        print('********* P%d elements:' % degree)
        n = 5
        for i in range(4):  # Run some resolutions
            n *= (i+1)
            mesh = generate_mesh(domain, n)
            #info(mesh)
            w = solver(p, Constant(0), mesh, degree=degree,
                       linear_solver='direct')
            print('max w: %g, w(0,0)=%g, h=%.3E, dofs=%d' %
                  (w.vector().array().max(), w((0,0)),
                   1/np.sqrt(mesh.num_vertices()),
                   w.function_space().dim()))

            w_exact = Expression('1 - x[0]*x[0] - x[1]*x[1]')
            w_e = interpolate(w_exact, w.function_space())
            error = np.abs(w_e.vector().array() -
                           w.vector().array()).max()
            print('error: %.3E' % error)
            assert error < 9.61E-03

def application2(
    beta, R0, num_elements_radial_dir):
    """Explore more built-in visulization features."""
    # Scaled pressure function
    p = Expression(
        '4*exp(-pow(beta,2)*(pow(x[0], 2) + pow(x[1]-R0, 2)))',
        beta=beta, R0=R0)

    # Generate mesh over the unit circle
    domain = Circle(Point(0.0, 0.0), 1.0)
    mesh = generate_mesh(domain, num_elements_radial_dir)

    w = solver(p, Constant(0), mesh, degree=1,
               linear_solver='direct')
    w.rename('w', 'deflection')

    # Plot scaled solution, mesh and pressure
    plot(mesh, title='Mesh over scaled domain')
    viz_w = plot(w,
                 wireframe=False,
                 title='Scaled membrane deflection',
                 axes=False,
                 interactive=False,
                 )
    viz_w.elevate(-10) # adjust (lift) camera from default view
    viz_w.plot(w)      # bring new settings into action
    viz_w.write_png('deflection')
    viz_w.write_pdf('deflection')

    V = w.function_space()
    p = interpolate(p, V)
    p.rename('p', 'pressure')
    viz_p = plot(p, title='Scaled pressure', interactive=False)
    viz_p.elevate(-10)
    viz_p.plot(p)
    viz_p.write_png('pressure')
    viz_p.write_pdf('pressure')

    # Dump w and p to file in VTK format
    vtkfile1 = File('membrane_deflection.pvd')
    vtkfile1 << w
    vtkfile2 = File('membrane_load.pvd')
    vtkfile2 << p

Filename: membrane_func.

• «
• 1
• ...
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• »