The goal of this chapter is to demonstrate how a range of important PDEs from science and engineering can be quickly solved with a few lines of FEniCS code. We start with the heat equation and continue with a nonlinear Poisson equation, the equations for linear elasticity, the Navier - Stokes equations, and finally look at how to solve systems of nonlinear advection - diffusion - reaction equations. These problems illustrate how to solve time-dependent problems, nonlinear problems, vector-valued problems, and systems of PDE. For each problem, we derive the variational formulation and express the problem in Python in a way that closely resembles the mathematics.
As a first extension of the Poisson problem from the previous chapter, we consider the time-dependent heat equation, or the time-dependent diffusion equation. This is the natural extension of the Poisson equation describing the stationary distribution of heat in a body to a time-dependent problem.
We will see that by discretizing time into small time intervals and applying standard time-stepping methods, we can solve the heat equation by solving a sequence of variational problems, much like the one we encountered for the Poisson equation.
Our model problem for time-dependent PDEs reads
Here, \(u\) varies with space and time, e.g., \(u=u(x,y,t)\) if the spatial domain \(\Omega\) is two-dimensional. The source function \(f\) and the boundary values \(u_{_\mathrm{D}}\) may also vary with space and time. The initial condition \(u_0\) is a function of space only.
A straightforward approach to solving time-dependent PDEs by the finite element method is to first discretize the time derivative by a finite difference approximation, which yields a sequence of stationary problems, and then turn each stationary problem into a variational formulation.
Let superscript \(n\) denote a quantity at time \(t_n\), where \(n\) is an integer counting time levels. For example, \(u^n\) means \(u\) at time level \(n\). A finite difference discretization in time first consists of sampling the PDE at some time level, say \(t_{n+1}\):
The time-derivative can be approximated by a difference quotient. For simplicity and stability reasons, we choose a simple backward difference:
where \({\Delta t}\) is the time discretization parameter. Inserting (21) in (20) yields
This is our time-discrete version of the heat equation (17). This is a so-called backward Euler or implicit Euler discretization. Alternatively, we may also view this as a finite element discretization in time in the form of the first order \(\mathrm{dG}(0)\) method, which here is identical to the backward Euler method.
We may reorder (22) so that the left-hand side contains the terms with the unknown \(u^{n+1}\) and the right-hand side contains computed terms only. The result is a sequence of spatial (stationary) problems for \(u^{n+1}\) (assuming \(u^n\) is known from computations at the previous time level):
Given \(u_0\), we can solve for \(u^0\), \(u^1\), \(u^2\), and so on.
An alternative to (24), which can be convenient in implementations, is to collect all terms on one side of the equality sign:
We use a finite element method to solve (23) and either of the equations (24) or (25). This requires turning the equations into weak forms. As usual, we multiply by a test function \(v\in \hat V\) and integrate second-derivatives by parts. Introducing the symbol \(u\) for \(u^{n+1}\) (which is natural in the program), the resulting weak form arising from formulation (24) can be conveniently written in the standard notation:
where
The alternative form (25) has an abstract formulation
where
In addition to the variational problem to be solved in each time step, we also need to approximate the initial condition (23). This equation can also be turned into a variational problem:
with
When solving this variational problem, \(u^0\) becomes the
\(L^2\) projection of the given initial value \(u_0\) into the finite
element space. The alternative is to construct \(u^0\) by just
interpolating the initial value \(u_0\); that is,
if \(u^0=\sum_{j=1}^N U^0_j\phi_j\), we simply set \(U_j=u_0(x_j,y_j)\),
where \((x_j,y_j)\) are the coordinates of node number \(j\). We refer to
these two strategies as computing the initial condition by either
projection or interpolation. Both operations are easy to
compute in FEniCS through one statement, using either the project or
interpolate function. The most common choice is project, which computes an
approximation to \(u_0\), but in some
applications where we want to verify the code by reproducing exact solutions,
one must use interpolate (and we use such a test problem!).
In summary, we thus need to solve the following sequence of variational problems to compute the finite element solution to the heat equation: find \(u^0\in V\) such that \(a_0(u^0,v)=L_0(v)\) holds for all \(v\in\hat V\), and then find \(u^{n+1}\in V\) such that \(a(u^{n+1},v)=L_{n+1}(v)\) for all \(v\in\hat V\), or alternatively, \(F(u^{n+1},v)=0\) for all \(v\in\hat V\), for \(n=0,1,2,\ldots\).
Our program needs to implement the time-stepping manually, but can rely on FEniCS to easily compute \(a_0\), \(L_0\), \(F\), \(a\), and \(L\), and solve the linear systems for the unknowns.
Just as for the Poisson problem from the previous chapter, we construct a test problem that makes it easy to determine if the calculations are correct. Since we know that our first-order time-stepping scheme is exact for linear functions, we create a test problem which has a linear variation in time. We combine this with a quadratic variation in space. We thus take
which yields a function whose computed values at the nodes will be exact, regardless of the size of the elements and \({\Delta t}\), as long as the mesh is uniformly partitioned. By inserting (31) into the heat equation (17), we find that the right-hand side \(f\) must be given by \(f(x,y,t)=\beta - 2 - 2\alpha\). The boundary value is \(u_{_\mathrm{D}}(x, y, t) = 1 + x^2 + \alpha y^2 + \beta t\) and the initial value is \(u_0(x, y) = 1 + x^2 + \alpha y^2\).
A new programming issue is how to deal with functions that vary in
space and time, such as the boundary condition \(u_{_\mathrm{D}}(x, y,
t) = 1 + x^2 + \alpha y^2 + \beta t\). A natural solution is to use a
FEniCS Expression with time \(t\) as a parameter, in addition to the
parameters \(\alpha\) and \(\beta\):
alpha = 3; beta = 1.2
u_D = Expression('1 + x[0]*x[0] + alpha*x[1]*x[1] + beta*t',
degree=2, alpha=alpha, beta=beta, t=0)
This expression uses the components of x as independent
variables, while alpha, beta, and t are parameters. The
parameters can later be updated as in
u_D.t = t
The essential boundary conditions, along the entire boundary in this case, are set in the usual way:
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
We shall use u for the unknown \(u^n\) at the new time level and u_n
for \(u^n\) at the previous time level. The initial value of u_n can be
computed by either projection or interpolation of \(u_0\). Since we set
t = 0 for the boundary value u_D, we can use this to also specify
the initial condition. We can then do
u_n = project(u_D, V)
# or
u_n = interpolate(u_D, V)
Projecting versus interpolating the initial condition
To actually recover the exact solution (31) to machine precision, it is important not to compute the discrete initial condition by projecting \(u_0\), but by interpolating \(u_0\) so that the degrees of freedom have exact values at \(t=0\) (projection results in approximate values at the nodes).
We may either define \(a\) or \(L\) according to the formulas above, or we may just define \(F\) and ask FEniCS to figure out which terms that go into the bilinear form \(a\) and which that go into the linear form \(L\). The latter is convenient, especially in more complicated problems, so we illustrate that construction of \(a\) and \(L\):
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(beta - 2 - 2*alpha)
F = u*v*dx + dt*dot(grad(u), grad(v))*dx - (u_n + dt*f)*v*dx
a, L = lhs(F), rhs(F)
Finally, we perform the time-stepping in a loop:
u = Function(V)
t = 0
for n in range(num_steps):
# Update current time
t += dt
u_D.t = t
# Solve variational problem
solve(a == L, u, bc)
# Update previous solution
u_n.assign(u)
In the last step of the time-stepping loop, we assign the values of
the variable u (the new computed solution) to the variable u_n
containing the values at the previous time step. This must be done
using the assign member function. If we instead try to do u_n = u,
we will set the u_n variable to be the same variable as u
which is not what we want. (We need two variables, one for the values
at the previous time step and one for the values at the current time
step.)
Remember to update expression objects with the current time
Inside the time loop,
observe that u_D.t must be updated before the solve statement
to enforce computation of Dirichlet conditions at the
current time level. (The Dirichlet conditions look up the u_D object
for values.)
The time loop above does not contain any comparison of the numerical
and the exact solution, which we must include in order to verify the
implementation. As in the Poisson equation example in
the section Dissection of the program, we compute the
difference between the array of nodal values for u and the array of
nodal values for
the interpolated exact solution. This may be done as follows:
u_e = interpolate(u_D, V)
error = np.abs(u_e.vector().array() - u.vector().array()).max()
print('error, t=%.2f: %.3g' % (t, error))
The complete program code for this time-dependent case goes as follows:
from fenics import *
import numpy as np
T = 2.0 # final time
num_steps = 10 # number of time steps
dt = T / num_steps # time step size
alpha = 3 # parameter alpha
beta = 1.2 # parameter beta
# Create mesh and define function space
nx = ny = 8
mesh = UnitSquareMesh(nx, ny)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary condition
u_D = Expression('1 + x[0]*x[0] + alpha*x[1]*x[1] + beta*t',
degree=2, alpha=alpha, beta=beta, t=0)
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
# Define initial value
u_n = interpolate(u_D, V)
#u_n = project(u_D, V)
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(beta - 2 - 2*alpha)
F = u*v*dx + dt*dot(grad(u), grad(v))*dx - (u_n + dt*f)*v*dx
a, L = lhs(F), rhs(F)
# Time-stepping
u = Function(V)
t = 0
for n in range(num_steps):
# Update current time
t += dt
u_D.t = t # update for bc
# Compute solution
solve(a == L, u, bc)
# Compute error at vertices
u_e = interpolate(u_D, V)
error = np.abs(u_e.vector().array() - u.vector().array()).max()
print('t = %.2f: error = %.3g' % (t, error))
# Update previous solution
u_n.assign(u)
The complete code can be found in the file ft04_heat.py.
Let’s solve a more interesting test problem, namely the diffusion of a Gaussian hill. We take the initial value to be given by
on the domain \([-2,2]\times [2,2]\). We will take \(a = 5\). For this problem we will use homogeneous Dirichlet boundary conditions (\(u_{_\mathrm{D}} = 0\)).
Which are the required changes to our previous program? One major
change is that the domain is not a unit square anymore. We also want to
use much higher resolution. The new domain can
be created easily in FEniCS using RectangleMesh:
nx = ny = 30
mesh = RectangleMesh(Point(-2, -2), Point(2, 2), nx, ny)
We also need to redefine the initial condition and boundary condition.
Both are easily changed by defining a new Expression and by setting
\(u = 0\) on the boundary. We will also save the solution to file in VTK
format in each time step:
vtkfile << (u, t)
The complete program appears below.
from fenics import *
import time
T = 2.0 # final time
num_steps = 50 # number of time steps
dt = T / num_steps # time step size
# Create mesh and define function space
nx = ny = 30
mesh = RectangleMesh(Point(-2,-2), Point(2,2), nx, ny)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary condition
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, Constant(0), boundary)
# Define initial value
u_0 = Expression('exp(-a*pow(x[0],2) - a*pow(x[1],2))',
degree=2, a=5)
u_n = interpolate(u_0, V)
u_n.rename('u', 'initial value')
vtkfile = File('gaussian_diffusion.pvd')
vtkfile << (u_n, 0.0)
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(0)
F = u*v*dx + dt*dot(grad(u), grad(v))*dx - (u_n + dt*f)*v*dx
a, L = lhs(F), rhs(F)
# Compute solution
u = Function(V)
u.rename('u', 'solution')
t = 0
for n in range(num_steps):
# Update current time
t += dt
# Solve variational problem
solve(a == L, u, bc)
# Save to file and plot solution
vtkfile << (u, float(t))
plot(u)
time.sleep(0.3)
# Update previous solution
u_n.assign(u)
The complete code can be found in the file ft05_gaussian_diffusion.py.
To visualize the diffusion of the Gaussian hill, start ParaView,
choose File - Open, open the file gaussian_diffusion.pvd, click
the green Apply button on the left to see the initial condition
being plotted. Choose View - Animation View. Click on the play
button or (better) the next frame button in the row of buttons at the
top of the GUI to see the evolution of the scalar field you have just
computed. Choose File - Save Animation... to save the animation to the AVI or OGG video format.
Once the animation has been saved to file, you can play the animation offline using a player such as mplayer or VLC, or upload your animation to YouTube. Below is a sequence of snapshots of the solution (first three time steps).
We shall now address how to solve nonlinear PDEs. We will see that
nonlinear problems can be solved just as easily as linear problems in
FEniCS, by simply defining a nonlinear variational problem and calling
the solve function. When doing so, we will encounter a subtle
difference in how the variational problem is defined.
As a sample PDE for the implementation of nonlinear problems, we take the following nonlinear Poisson equation:
in \(\Omega\), with \(u=u_{_\mathrm{D}}\) on the boundary \(\partial\Omega\). The coefficient \(q(u)\) makes the equation nonlinear (unless \(q(u)\) is constant in \(u\)).
As usual, we multiply our PDE by a test function \(v\in\hat V\), integrate over the domain, and integrate the second-order derivatives by parts. The boundary integral arising from integration by parts vanishes wherever we employ Dirichlet conditions. The resulting variational formulation of our model problem becomes: find \(u \in V\) such that
where
and
The discrete problem arises as usual by restricting \(V\) and \(\hat V\) to a pair of discrete spaces. As before, we omit any subscript on the discrete spaces and discrete solution. The discrete nonlinear problem is then written as: Find \(u\in V\) such that
with \(u = \sum_{j=1}^N U_j \phi_j\). Since \(F\) is nonlinear in \(u\), the variational statement gives rise to a system of nonlinear algebraic equations in the unknowns \(U_1,\ldots,U_N\).
To solve a test problem, we need to choose the right-hand side \(f\),
the coefficient \(q(u)\) and the boundary value \(u_{_\mathrm{D}}\). Previously, we
have worked with manufactured solutions that can be reproduced without
approximation errors. This is more difficult in nonlinear problems,
and the algebra is more tedious. However, we may utilize SymPy for
symbolic computing and integrate such computations in the FEniCS
solver. This allows us to easily experiment with different
manufactured solutions. The forthcoming code with SymPy requires some
basic familiarity with this package. In particular, we will use the
SymPy functions diff for symbolic differentiation and ccode for
C/C++ code generation.
We try out a two-dimensional manufactured solution that is linear in the unknowns:
# Warning: from fenics import * will import both `sym` and
# `q` from FEniCS. We therefore import FEniCS first and then
# overwrite these objects.
from fenics import *
def q(u):
"""Nonlinear coefficient in the PDE."""
return 1 + u**2
# Use SymPy to compute f given manufactured solution u
import sympy as sym
x, y = sym.symbols('x[0] x[1]')
u = 1 + x + 2*y
f = - sym.diff(q(u)*sym.diff(u, x), x) - \
sym.diff(q(u)*sym.diff(u, y), y)
f = sym.simplify(f)
u_code = sym.printing.ccode(u)
f_code = sym.printing.ccode(f)
print('u =', u_code)
print('f =', f_code)
Define symbolic coordinates as required in Expression objects
Note that we would normally write x, y = sym.symbols('x y'), but
if we want the resulting expressions to have valid syntax for
FEniCS Expression objects, we must use x[0] and x[1].
This is easily accomplished with sympy by defining the names of x and
y as x[0] and x[1]: x, y = sym.symbols('x[0] x[1]').
Turning the expressions for u and f into C or C++ syntax for
FEniCS Expression objects needs two steps. First, we ask for the C
code of the expressions:
u_code = sym.printing.ccode(u)
f_code = sym.printing.ccode(f)
Sometimes, we need some editing of the result to match the required
syntax of Expression objects, but not in this case. (The primary
example is that M_PI for \(\pi\) in C/C++ must be replaced by pi for
Expression objects.) In the present case, the output of c_code and
f_code is
x[0] + 2*x[1] + 1
-10*x[0] - 20*x[1] - 10
After having defined the mesh, the function space, and the boundary,
we define the boundary value u_D as
u_D = Expression(u_code)
Similarly, we define the right-hand side function as
f = Expression(f_code)
Name clash between FEniCS and program variables
In a program like the one above, strange errors may occur due to
name clashes. If you define sym and q prior to doing
from fenics import *, the latter statement will also import
variables with the names sym and q, overwriting
the objects you have previously defined! This may lead to strange
errors. The safest solution is to do import fenics as fe
and then prefix all FEniCS
object names by fe. The next best solution is to do
from fenics import * first and then define your own variables
that overwrite those imported from fenics. This is acceptable
if we do not need sym and q from fenics.
A working solver for the nonlinear Poisson equation is as easy to
implement as a solver for the corresponding linear problem.
All we need to do is to state the formula for \(F\) and call
solve(F == 0, u, bc) instead of solve(a == L, u, bc) as we did
in the linear case. Here is a minimalistic code:
from fenics import *
def q(u):
return 1 + u**2
mesh = UnitSquareMesh(32, 32)
V = FunctionSpace(mesh, 'P', 1)
u_D = Expression(...)
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
u = Function(V)
v = TestFunction(V)
f = Expression(...)
F = q(u)*dot(grad(u), grad(v))*dx - f*v*dx
solve(F == 0, u, bc)
The complete code can be found in the file ft06_poisson_nonlinear.py.
The major difference from a linear problem is that the unknown function
u in the variational form in the nonlinear case
must be defined as a Function, not as a TrialFunction. In some sense
this is a simplification from the linear case where we must define u
first as a TrialFunction and then as a Function.
The solve function takes the nonlinear equations, derives symbolically
the Jacobian matrix, and runs a Newton method to compute the solution.
# Warning: from fenics import * will import both `sym` and
# `q` from FEniCS. We therefore import FEniCS first and then
# overwrite these objects.
from fenics import *
def q(u):
"""Nonlinear coefficient in the PDE."""
return 1 + u**2
# Use SymPy to compute f given manufactured solution u
import sympy as sym
x, y = sym.symbols('x[0] x[1]')
u = 1 + x + 2*y
f = - sym.diff(q(u)*sym.diff(u, x), x) - \
sym.diff(q(u)*sym.diff(u, y), y)
f = sym.simplify(f)
u_code = sym.printing.ccode(u)
f_code = sym.printing.ccode(f)
print('u =', u_code)
print('f =', f_code)
# Create mesh and define function space
mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary condition
u_D = Expression(u_code, degree=2)
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
# Define variational problem
u = Function(V) # not TrialFunction!
v = TestFunction(V)
f = Expression(f_code, degree=2)
F = q(u)*dot(grad(u), grad(v))*dx - f*v*dx
# Compute solution
solve(F == 0, u, bc)
# Plot solution
u.rename('u', 'solution')
plot(u)
# Compute error at vertices
u_e = interpolate(u_D, V)
import numpy as np
error = np.abs(u_e.vector().array() - u.vector().array()).max()
print('error = %.3g' % error)
# Hold plot
interactive()
Running the code gives output that tells how the Newton iteration progresses. With \(2\cdot(8\times 8)\) cells we reach convergence in 8 iterations with a tolerance of \(10^{-9}\), and the error in the numerical solution is about \(10^{-16}\). These results bring evidence for a correct implementation. Thinking in terms of finite differences on a uniform mesh, \(\mathcal{P}_1\) elements mimic standard second-order differences, which compute the derivative of a linear or quadratic function exactly. Here, \(\nabla u\) is a constant vector, but then multiplied by \((1+u^2)\), which is a second-order polynomial in \(x\) and \(y\), which the divergence “difference operator” should compute exactly. We can therefore, even with \(\mathcal{P}_1\) elements, expect the manufactured \(u\) to be reproduced by the numerical method. With a nonlinearity like \(1+u^4\), this will not be the case, and we would need to verify convergence rates instead.
The current example shows how easy it is to solve a nonlinear problem in FEniCS. However, experts on the numerical solution of nonlinear PDEs know very well that automated procedures may fail in nonlinear problems, and that it is often necessary to have much better manual control of the solution process than what we have in the current case. Therefore, we return to this problem in the chapter “Implementing solvers for nonlinear PDEs”: “” [Ref25] and show how we can implement our own solution algorithms for nonlinear equations and also how we can steer the parameters in the automated Newton method used above. You will then see how easy it is to implement tailored solution strategies for nonlinear problems in FEniCS.
Analysis of structures is one of the major activities of modern engineering, thus making the PDEs for deformation of elastic bodies likely the most popular PDE model in the world. It takes just one page of code to solve the equations of 2D or 3D elasticity in FEniCS, and the details follow below.
The equations governing small elastic deformations of a body \(\Omega\) can be written as
where \(\sigma\) is the stress tensor, \(f\) is the body force per unit volume, \(\lambda\) and \(\mu\) are \(\text{Lam\'e's}\) elasticity parameters for the material in \(\Omega\), \(I\) is the identity tensor, \(\mathrm{tr}\) is the trace operator on a tensor, \(\varepsilon\) is the strain tensor (symmetric gradient), and \(u\) is the displacement vector field. We have here assumed isotropic elastic conditions.
We combine (37) and (38) to obtain
Note that (36)–(38) can easily be transformed to a single vector PDE for \(u\), which is the governing PDE for the unknown \(u\) (Navier’s equation). In the derivation of the variational formulation, however, it is convenient to keep the splitting of the equations as above.
The variational formulation of (36)–(38) consists of forming the inner product of (36) and a vector test function \(v\in \hat{V}\), where \(\hat{V}\) is a vector-valued test function space, and integrating over the domain \(\Omega\):
Since \(\nabla\cdot\sigma\) contains second-order derivatives of the primary unknown \(u\), we integrate this term by parts:
where the colon operator is the inner product between tensors (summed pairwise product of all elements), and \(n\) is the outward unit normal at the boundary. The quantity \(\sigma\cdot n\) is known as the traction or stress vector at the boundary, and is often prescribed as a boundary condition. We assume that it is prescribed at a part \(\partial\Omega_T\) of the boundary as \(\sigma\cdot n = T\). On the remaining part of the boundary, we assume that the value of the displacement is given as a Dirichlet condition. We then have
Inserting the expression (39) for \(\sigma\) gives the variational form with \(u\) as unknown. Note that the boundary integral on the remaining part \(\partial\Omega\setminus\Omega_T\) vanishes due to the Dirichlet condition (\(v = 0\)).
We can now summarize the variational formulation as: find \(u\in V\) such that
where
One can show that the inner product of a symmetric tensor \(A\) and a anti-symmetric tensor \(B\) vanishes. If we express \(\nabla v\) as a sum of its symmetric and anti-symmetric parts, only the symmetric part will survive in the product \(\sigma :\nabla v\) since \(\sigma\) is a symmetric tensor. Thus replacing \(\nabla u\) by the symmetric gradient \(\epsilon(u)\) gives rise to the slightly different variational form
where \(\varepsilon(v)\) is the symmetric part of \(\nabla v\):
The formulation (44) is what naturally arises from minimization of elastic potential energy and is a more popular formulation than (41).
As a test example, we may look at a clamped beam deformed under its own weight. Then \(f=(0,0,-\varrho g)\) is the body force per unit volume with \(\varrho\) the density of the beam and \(g\) the acceleration of gravity. The beam is box-shaped with length \(L\) and has a square cross section of width \(W\). We set \(u=u_{_\mathrm{D}} = (0,0,0)\) at the clamped end, \(x=0\). The rest of the boundary is traction free; that is, we set \(T = 0\).
We first list the code and then comment upon the new constructions compared to the Poisson equation case.
from fenics import *
# Scaled variables
L = 1; W = 0.2
mu = 1
rho = 1
delta = W/L
gamma = 0.4*delta**2
beta = 1.25
lambda_ = beta
g = gamma
# Create mesh and define function space
mesh = BoxMesh(Point(0, 0, 0), Point(L, W, W), 10, 3, 3)
V = VectorFunctionSpace(mesh, 'P', 1)
# Define boundary conditions
tol = 1E-14
def clamped_boundary(x, on_boundary):
return on_boundary and x[0] < tol
bc = DirichletBC(V, Constant((0, 0, 0)), clamped_boundary)
# Define strain and stress
def epsilon(u):
return 0.5*(nabla_grad(u) + nabla_grad(u).T)
#return sym(nabla_grad(u))
def sigma(u):
return lambda_*nabla_div(u)*Identity(d) + 2*mu*epsilon(u)
# Define variational problem
u = TrialFunction(V)
d = u.geometric_dimension() # no of space dim
v = TestFunction(V)
f = Constant((0, 0, rho*g))
T = Constant((0, 0, 0))
a = inner(sigma(u), epsilon(v))*dx
L = dot(f, v)*dx + dot(T, v)*ds
# Compute solution
u = Function(V)
solve(a == L, u, bc)
# Plot solution
plot(u, title='Displacement', mode='displacement')
# Plot stress
s = sigma(u) - (1./3)*tr(sigma(u))*Identity(d) # deviatoric stress
von_Mises = sqrt(3./2*inner(s, s))
V = FunctionSpace(mesh, 'P', 1)
von_Mises = project(von_Mises, V)
plot(von_Mises, title='Stress intensity')
# Compute magnitude of displacement
u_magnitude = sqrt(dot(u, u))
u_magnitude = project(u_magnitude, V)
plot(u_magnitude, 'Displacement magnitude')
print('min/max u:', u_magnitude.vector().array().min(),
u_magnitude.vector().array().max())
The complete code can be found in the file ft07_elasticity.py.
We comment below on some of the key features of this example that we have not seen in previous examples.
The primary unknown is now a vector field \(u\) and not a scalar field, so we need to work with a vector function space:
V = VectorFunctionSpace(mesh, 'P', 1)
With u = Function(V) we get u as a vector-valued finite element function.
In the boundary condition \(u=0\), we must set a vector value to zero, not just
a scalar, and a constant zero vector is specified as Constant((0, 0, 0)) in
FEniCS. The corresponding 2D code would use Constant((0, 0)).
Later in the code, we also need f as a vector and specify it
as Constant((0, 0, rho*g)).
nabla_grad¶The gradient and divergence operators now have a prefix nabla_.
This is strictly not necessary in the present problem, but
recommended in general for vector PDEs arising from continuum mechanics,
if you interpret \(\nabla\) as a vector in the PDE notation;
see the box about nabla_grad in the section Variational formulation.
As soon as u is computed, we can compute various stress measures, here
the von Mises stress defined as \(\sigma_M = \sqrt{\frac{3}{2}s:s}\)
where \(s\) is the deviatoric stress tensor
There is a one to one mapping between these formulas and the FEniCS code:
s = sigma(u) - (1./3)*tr(sigma(u))*Identity(d)
von_Mises = sqrt(3./2*inner(s, s))
The von_Mises variable is now an expression that must be projected to
a finite element space before we can visualize it.
Before doing simulations for a specific problem, it is often advantageous to scale the problem as it reduces the need for setting physical parameters, and one obtains dimensionsless numbers that reflect the competition of parameters and physical effects. We develop the code for the original model with dimensions, and run the scaled problem by tweaking parameters appropriately. Scaling reduces the number of active parameters from 6 to 2 in the present application.
In Navier’s equation for \(u\), arising from inserting (37) and (38) in (36),
we insert coordinates made dimensionless by \(L\), and \(\bar u=u/U\), which results in the dimensionless governing equation
where \(\beta = \lambda/\mu\) is a dimensionless elasticity parameter and
is also a dimensionless variable reflecting the ratio of the load \(\varrho g\) and the shear stress term \(\mu\nabla^2 u\sim \mu U/L^2\) in the PDE.
Sometimes, one will argue to chose \(U\) to make \(\gamma\) unity (\(U = \varrho gL^2/\mu\)). However, in elasticity, this leads us to displacements of the size of the geometry, which makes plots look very strange. We therefore want the characteristic displacement to be a small fraction of the characteristic length of the geometry. This can be achieved by choosing \(U\) equal to the maximum deflection of a clamped beam, for which there actually exists an formula: \(U = \frac{3}{2}\varrho gL^2\delta^2/E\), where \(\delta = L/W\) is a parameter reflecting how slender the beam is, and \(E\) is the modulus of elasticity. Thus, the dimensionless parameter \(\delta\) is very important in the problem (as expected, since \(\delta\gg 1\) is what gives beam theory!). Taking \(E\) to be of the same order as \(\mu\), which is the case for many materials, we realize that \(\gamma \sim \delta^{-2}\) is an appropriate choice. Experimenting with the code to find a displacement that “looks right” in plots of the deformed geometry, points to \(\gamma = 0.4\delta^{-2}\) as our final choice of \(\gamma\).
The simulation code implements the problem with dimensions and physical parameters \(\lambda\), \(\mu\), \(\varrho\), \(g\), \(L\), and \(W\). However, we can easily reuse this code for a scaled problem: just set \(\mu = \varrho = L = 1\), \(W\) as \(W/L\) (\(\delta^{-1}\)), \(g=\gamma\), and \(\lambda=\beta\).
The problems we have encountered so far—with the notable exception of the Navier - Stokes equations—all share a common feature: they all involve models expressed by a single scalar or vector PDE. In many situations the model is instead expressed as a system of PDEs, describing different quantities and with possibly (very) different physics. As we saw for the Navier - Stokes equations, one way to solve a system of PDEs in FEniCS is to use a splitting method where we solve one equation at a time and feed the solution from one equation into the next. However, one of the strengths with FEniCS is the ease by which one can instead define variational problems that couple several PDEs into one compound system. In this section, we will look at how to use FEniCS to write solvers for such systems of coupled PDEs. The goal is to demonstrate how easy it is to implement fully implicit, also known as monolithic, solvers in FEniCS.
Our model problem is the following system of advection - diffusion - reaction equations:
This system models the chemical reaction between two species \(A\) and \(B\) in some domain \(\Omega\):
We assume that the equation is first-order, meaning that the reaction rate is proportional to the concentrations \([A]\) and \([B]\) of the two species \(A\) and \(B\):
We also assume that the formed species \(C\) spontaneously decays with a rate proportional to the concentration \([C]\). In the PDE system (53)–(55), we use the variables \(u_1\), \(u_2\), and \(u_3\) to denote the concentrations of the three species:
We see that the chemical reactions are accounted for in the right-hand sides of the PDE system (53)–(55).
The chemical reactions take part at each point in the domain \(\Omega\). In addition, we assume that the species \(A\), \(B\), and \(C\) diffuse throughout the domain with diffusivity \(\epsilon\) (the terms \(-\nabla\cdot(\epsilon\nabla u_i)\)) and are advected with velocity \(w\) (terms like \(w\cdot\nabla u_i\)).
To make things visually and physically interesting, we shall let the chemical reaction take place in the velocity field computed from the solution of the incompressible Navier - Stokes equations around a cylinder from the previous section. In summary, we will thus be solving the following coupled system of nonlinear PDEs:
We assume that \(u_1 = u_2 = u_3 = 0\) at \(t = 0\) and inject the species \(A\) and \(B\) into the system by specifying nonzero source terms \(f_1\) and \(f_2\) close to the corners at the inflow, and take \(f_3 = 0\). The result will be that \(A\) and \(B\) are convected by advection and diffusion throughout the channel, and when they mix the species \(C\) will be formed.
Since the system is one-way coupled from the Navier - Stokes subsystem to the advection - diffusion - reaction subsystem, we do not need to recompute the solution to the Navier - Stokes equations, but can just read back the previously computed velocity field \(w\) and feed it into our equations. But we do need to learn how to read and write solutions from time-dependent PDE problems.
We obtain the variational formulation of our system by multiplying each equation by a test function, integrating the second-order terms \(-\nabla\cdot(\epsilon\nabla u_i)\) by parts, and summing up the equations. When working with FEniCS it is convenient to think of the PDE system as a vector of equations. The test functions are collected in a vector too, and the variational formulation is the inner product of the vector PDE and the vector test function.
We also need introduce some discretization in time. We will use the backward Euler method as before when we solved the heat equation and approximate the time derivatives by \((u_i^{n+1}-u_i^n) / {\Delta t}\). Let \(v_1\), \(v_2\), and \(v_3\) be the test functions, or the components of the test vector function. The inner product results in
For this problem it is natural to assume homogeneous Neumann boundary conditions on the entire boundary for \(u_1\), \(u_2\), and \(u_3\); that is, \(\partial u_i/\partial n = 0\) for \(i = 1, 2, 3\). This means that the boundary terms vanish when we integrate by parts.
The first step is to read the mesh from file. Luckily, we made sure to save the mesh to file in the Navier - Stokes example and can now easily read it back from file:
mesh = Mesh(cylinder.xml.gz')
The mesh is stored in the native FEniCS XML format (with additional gzipping to decrease the file size).
Next, we need to define the finite element function space. For this problem, we need to define several spaces. The first space we create is the space for the velocity field \(w\) from the Navier - Stokes simulation. We call this space \(W\) and define the space by
W = VectorFunctionSpace(mesh, 'P', 2)
It is important that this space is exactly the same as the space we
used for the velocity field in the Navier - Stokes solver. To read the
values for the velocity field, we use a TimeSeries:
timeseries_w = TimeSeries('navier_stokes_cylinder/velocity')
This will initialize the object timeseries_w which we will call
later in the time-stepping loop to retrieve values from the
file velocity.h5 (in binary HDF5 format).
For the three concentrations \(u_1\), \(u_2\), and \(u_3\), we want to
create a mixed space with functions that represent the full system
\((u_1, u_2, u_3)\) as a single entity. To do this, we need to define a
MixedElement as the product space of three simple finite elements
and then used the mixed element to define the function space:
P1 = FiniteElement('P', 'triangle', 1)
element = MixedElement([P1, P1, P1])
V = FunctionSpace(mesh, element)
Mixed elements as products of elements
FEniCS also allows finite elements to be defined as products of simple elements (or mixed elements). For example, the well-known Taylor - Hood element, with quadratic velocity components and linear pressure functions, may be defined as follows:
P2 = VectorElement('P', 'triangle', 2)
P1 = FiniteElement('P', 'triangle', 1)
TH = P2 * P1
This syntax works great for two elements, but for three or more
elements we meet a subtle issue in how the Python interpreter handles
the * operator. For the reaction system, we create the mixed element
by element = MixedElement([P1, P1, P1]) and one would be tempted to
write
element = P1 * P1 * P1
However, this is equivalent to writing element = (P1 * P1) * P1 so
the result will be a mixed element consisting of two subsystems, the
first of which in turn consists of two scalar subsystems.
Finally, we remark that for the simple case of a mixed system consisting of three scalar elements as for the reaction system, the definition is in fact equivalent to using a standard vector-valued element:
element = VectorElement('P', 'triangle', 1, dim=3)
V = FunctionSpace(mesh, element)
Once the space has been created, we need to define our test functions
and finite element functions. Test functions for a mixed function
space can be created by replacing TestFunction by TestFunctions:
v_1, v_2, v_3 = TestFunctions(V)
Since the problem is nonlinear, we need to work with functions rather
than trial functions for the unknowns. This can be done by using the
corresponding Functions construction in FEniCS. However, as we will
need to access the Function for the entire system itself, we first
need to create that function and then access its components:
u = Function(V)
u_1, u_2, u_3 = split(u)
These functions will be used to represent the unknowns \(u_1\), \(u_2\), and \(u_3\)
at the new time level \(n+1\). The corresponding values at the previous
time level \(n\) are denoted by u_n1, u_n2, and u_n3 in our program.
When now all functions and test functions have been defined, we can express the nonlinear variational problem (61):
F = ((u_1 - u_n1) / k)*v_1*dx + dot(w, grad(u_1))*v_1*dx \
+ eps*dot(grad(u_1), grad(v_1))*dx + K*u_1*u_2*v_1*dx \
+ ((u_2 - u_n2) / k)*v_2*dx + dot(w, grad(u_2))*v_2*dx \
+ eps*dot(grad(u_2), grad(v_2))*dx + K*u_1*u_2*v_2*dx \
+ ((u_3 - u_n3) / k)*v_3*dx + dot(w, grad(u_3))*v_3*dx \
+ eps*dot(grad(u_3), grad(v_3))*dx - K*u_1*u_2*v_3*dx + K*u_3*v_3*dx \
- f_1*v_1*dx - f_2*v_2*dx - f_3*v_3*dx
The time-stepping simply consists of solving this variational problem
in each time step by a call to the solve function:
t = 0
for n in range(num_steps):
t += dt
timeseries_w.retrieve(w.vector(), t)
solve(F == 0, u)
u_n.assign(u)
In each time step, we first read the current value for the velocity field from the time series we have previously stored. We then solve the nonlinear system, and assign the computed values to the left-hand side values for the next time interval.
The solution at the final time is shown in Figure Plot of the concentrations of the three species \( A \) , \( B \) , and \( C \) (from top to bottom) at final time. We clearly see the advection of the species \(A\) and \(B\) and the formation of \(C\) along the center of the channel where \(A\) and \(B\) meet.
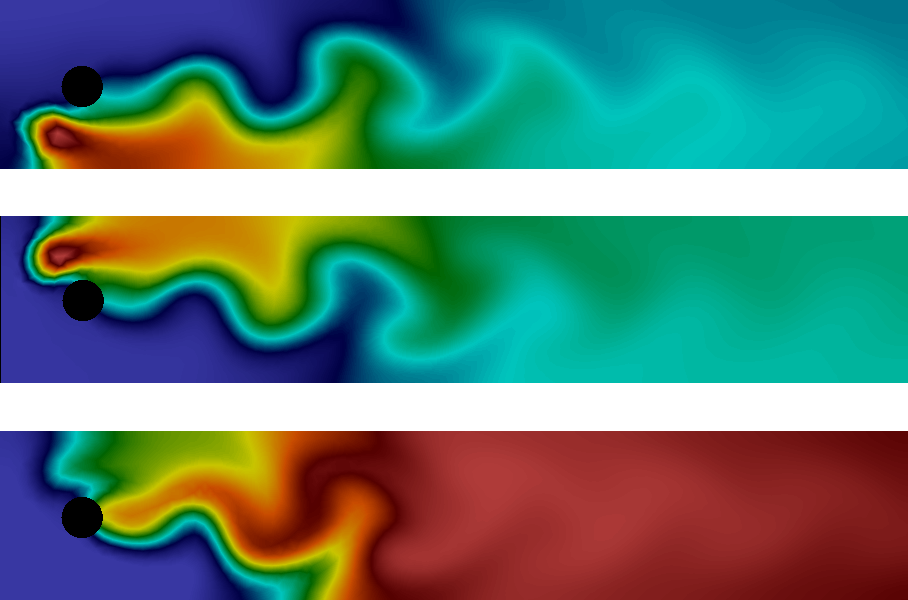
Plot of the concentrations of the three species \( A \) , \( B \) , and \( C \) (from top to bottom) at final time
The complete code is presented below.
from fenics import *
T = 5.0 # final time
num_steps = 500 # number of time steps
dt = T / num_steps # time step size
eps = 0.01 # diffusion coefficient
K = 10.0 # reaction rate
# Read mesh from file
mesh = Mesh('cylinder.xml.gz')
# Define function space for velocity
W = VectorFunctionSpace(mesh, 'P', 2)
# Define function space for system of concentrations
P1 = FiniteElement('P', 'triangle', 1)
element = MixedElement([P1, P1, P1])
V = FunctionSpace(mesh, element)
# Define test functions
v_1, v_2, v_3 = TestFunctions(V)
# Define functions for velocity and concentrations
w = Function(W)
u = Function(V)
u_n = Function(V)
# Split system functions to access components
u_1, u_2, u_3 = split(u)
u_n1, u_n2, u_n3 = split(u_n)
# Define source terms
f_1 = Expression('pow(x[0]-0.1,2)+pow(x[1]-0.1,2)<0.05*0.05 ? 0.1 : 0',
degree=1)
f_2 = Expression('pow(x[0]-0.1,2)+pow(x[1]-0.3,2)<0.05*0.05 ? 0.1 : 0',
degree=1)
f_3 = Constant(0)
# Define expressions used in variational forms
k = Constant(dt)
K = Constant(K)
eps = Constant(eps)
# Define variational problem
F = ((u_1 - u_n1) / k)*v_1*dx + dot(w, grad(u_1))*v_1*dx \
+ eps*dot(grad(u_1), grad(v_1))*dx + K*u_1*u_2*v_1*dx \
+ ((u_2 - u_n2) / k)*v_2*dx + dot(w, grad(u_2))*v_2*dx \
+ eps*dot(grad(u_2), grad(v_2))*dx + K*u_1*u_2*v_2*dx \
+ ((u_3 - u_n3) / k)*v_3*dx + dot(w, grad(u_3))*v_3*dx \
+ eps*dot(grad(u_3), grad(v_3))*dx - K*u_1*u_2*v_3*dx + K*u_3*v_3*dx \
- f_1*v_1*dx - f_2*v_2*dx - f_3*v_3*dx
# Create time series for reading velocity data
timeseries_w = TimeSeries('navier_stokes_cylinder/velocity')
# Create VTK files for visualization output
vtkfile_u_1 = File('reaction_system/u_1.pvd')
vtkfile_u_2 = File('reaction_system/u_2.pvd')
vtkfile_u_3 = File('reaction_system/u_3.pvd')
# Create progress bar
progress = Progress('Time-stepping')
set_log_level(PROGRESS)
# Time-stepping
t = 0
for n in range(num_steps):
# Update current time
t += dt
# Read velocity from file
timeseries_w.retrieve(w.vector(), t)
# Solve variational problem for time step
solve(F == 0, u)
# Save solution to file (VTK)
_u_1, _u_2, _u_3 = u.split()
vtkfile_u_1 << _u_1
vtkfile_u_2 << _u_2
vtkfile_u_3 << _u_3
# Update previous solution
u_n.assign(u)
# Update progress bar
progress.update(t / T)
# Hold plot
interactive()
The complete code can be found in the file ft10_reaction_system.py.
Finally, we comment on three important techniques that are very useful when working with systems of PDEs: setting initial conditions, setting boundary conditions, and extracting components of the system for plotting or postprocessing.
In our example, we did not need to worry about setting an initial
condition, since we start with \(u_1 = u_2 = u_3 = 0\). This happens
automatically in the code when we set u_n = Function(V). This
creates a Function for the whole system and all degrees of freedom
are set to zero.
If we want to set initial conditions for the components of the
system separately, the easiest solution is to define the initial
conditions as a vector-valued Expression and then
project this to the Function representing the whole system. For
example,
u_0 = Expression(('sin(x[0])', 'cos(x[0]*x[1])', 'exp(x[1])'), degree=1)
u_n = project(u_0, V)
This defines \(u_1\), \(u_2\), and \(u_2\) to be the projections of \(\sin x\), \(\cos (xy)\), and \(\exp(y)\), respectively.
In our example, we also did not need to worry about setting boundary
conditions since we used a natural Neumann condition. If we want to set
Dirichlet conditions for individual components of the system, this can
be done as usual by the class DirichletBC, but we must specify for
which subsystem we set the boundary condition. For example, to specify
that \(u_2\) should be equal to \(xy\) on the boundary defined by
boundary, we do
u_D = Expression('x[0]*x[1]', degree=1)
bc = DirichletBC(V.sub(1), u_D, boundary)
The object bc or a list of such objects containing different
boundary conditions, can then be passed to the solve function as usual.
Note that numbering starts at \(0\) in FEniCS so the subspace
corresponding to \(u_2\) is V.sub(1).
If u is a Function defined on a mixed function space in FEniCS,
there are several ways in which u can be split into components.
Above we already saw an example of the first of these:
u_1, u_2, u_3 = split(u)
This extracts the components of u as symbols that can be used in a
variational problem. The above statement is in fact equivalent to
u_1 = u[0]
u_2 = u[1]
u_3 = u[2]
Note that u[0] is not really a Function object, but merely a
symbolic expression, just like grad(u) in FEniCS is a symbolic
expression and not a Function representing the gradient. This means
that u_1, u_2, u_3 can be used in a variational problem, but
cannot be used for plotting or postprocessing.
To access the components of u for plotting and saving the solution
to file, we need to use a different variant of the split function:
_u_1, _u_2, _u_3 = u.split()
This returns three subfunctions as actual objects with access to the
common underlying data stored in u, which makes plotting and saving
to file possible. Alternatively, we can do
_u_1, _u_2, _u_3 = u.split(deepcopy=True)
which will create _u_1, _u_2, and u_3 as stand-alone Function
objects, each holding a copy of the subfunction data extracted from
u. This is useful in many situations but is not necessary for
plotting and saving solutions to file.