Using Flask for Scientific Web Applications

Autogenerating the code

We shall now present generic model.py and controller.py files that work with any compute function (!). This example will demonstrate some advanced, powerful features of Python. The source code is found in the gen directory.

Inspecting function signatures

The basic idea is that the Python module inspect can be used to retrieve the names of the arguments and the default values of keyword arguments of any given compute function. Say we have some

def mycompute(A, m=0, s=1, w=1, x_range=[-3,3]):
    ...
    return result

Running

import inspect
arg_names = inspect.getargspec(mycompute).args
defaults  = inspect.getargspec(mycompute).defaults

leads to

arg_names = ['A', 'm', 's', 'w', 'x_range']
defaults = (0, 1, 1, [-3, 3])

We have all the argument names in arg_names and defaults[i] is the default value of keyword argument arg_names[j], where j = len(arg_names) - len(defaults) + i.

Generating the model

Knowing the name name of some argument in the compute function, we can make the corresponding class attribute in the InputForm class by

setattr(InputForm, name, FloatForm())

For name equal to 'A' this is the same as hardcoding

class InputForm:
    A = FloatForm()

Assuming that all arguments in compute are floats, we could do

class InputForm:
    pass  # Empty class

arg_names = inspect.getargspec(mycompute).args
for name in arg_names:
    setattr(InputForm, name, FloatForm())

However, we can do better than this: for keyword arguments the type of the default value can be used to select the appropriate form class. The complete model.py file then goes as follows:

"""
Example on generic model.py file which inspects the arguments
of the compute function and automatically generates a relevant
InputForm class.
"""

import wtforms
from math import pi

from compute import compute_gamma as compute
import inspect
arg_names = inspect.getargspec(compute).args
defaults  = inspect.getargspec(compute).defaults

class InputForm(wtforms.Form):
    pass

# Augment defaults with None elements for the positional
# arguments
defaults = [None]*(len(arg_names)-len(defaults)) + list(defaults)
# Map type of default to right form field
type2form = {type(1.0): wtforms.FloatField,
             type(1):   wtforms.IntegerField,
             type(''):  wtforms.TextField,
             }

for name, value in zip(arg_names, defaults):
    if value is None:
        setattr(InputForm, name, wtforms.FloatField(
            validators=[wtforms.validators.InputRequired()]))
    else:
        if type(value) in type2form:
            setattr(InputForm, name, type2form[type(value)](
                default=value,
                validators=[wtforms.validators.InputRequired()]))
        else:
            raise TypeError('argument %s %s not supported' %
                            name, type(value))

if __name__ == '__main__':
    for item in dir(InputForm):
        if item in arg_names:
            print item, getattr(InputForm, item)

(The compute_gamma function imported from compute is the only application-specific statement in this code and will be explained later.)

Generating the view

The call to compute in the controller.py file must also be expressed in a general way such that the call handles any type and number of parameters. This can be done in two ways, using either positional or keyword arguments.

The technique with positional arguments is explained first. It consists of collecting all parameters in a list or tuple, called args, and then calling compute(*args) (which is equivalent to compute(args[0], args[1], ..., args[n]) if n is len(args)-1). The elements of args are the values of the form variables. We know the name of a form variable as a string name (from arg_names), and if form is the form object, the construction getattr(form, name).data extracts the value that the user provided (getattr(obj, attr) gets the attribute, with name available as a string in attr, in the object obj). For exampe, if name is 'A', getattr(form, name).data is the same as form.A.data. Collecting all form variables, placing them in a list, and calling compute are done with

arg_names = inspect.getargspec(compute).args
args = [getattr(form, name).data for name in arg_names]
result = compute(*args)

Our InputForm class guarantees that all arguments in compute are present in the form, but to be absolutely safe we can test if name is present in the form object:

args = [getattr(form, name).data for name in arg_names
        if hasattr(form, name)]

A potential problem with the args list is that the values might be in wrong order. It appears, fortunately, that the order we assign attributes to the form class is preserved when iterating over the form. Nevertheless, using keyword arguments instead of positional arguments provides a completely safe solution to calling compute with the correct arguments. Keyword arguments are placed in a dictionary kwargs and compute is called as compute(**kwargs). The generic solution is

kwargs = {name: getattr(form, name).data for name in arg_names
          if hasattr(form, name)}
result = compute(**kwargs)

The compute(**kwargs) call is equivalent to compute(A=1, b=3, w=0.5) in case kwargs = {'w'=0.5, 'A':1, 'b':3} (recall that the order of the keys in a Python dictionary is undetermined).

Generating the template

It remains to generate the right HTML template. The HTML code depends on what the returned result object from compute contains. Only a human who has read the compute code knows the details of the returned result. Therefore, we leave it to a human to provide the part of the HTML template that renders the result. The file templates/view_results.html contains this human-provided code, while templates/view.html is a completely generic template for the forms:

<form method=post action="">
<table>
  {% for field in form %}
    <tr><td>{{ field.name }}</td> <td>{{ field }}</td>
    <td>{% if field.errors %}
      <ul class=errors>
      {% for error in field.errors %}
        <li>{{ error }}</li>
      {% endfor %}</ul>
    {% endif %}</td></tr>
  {% endfor %}
</table>
<p><input type=submit value=Compute></form></p>

{% if result != None %}
{{ result|safe }}
{% endif %}

At the end of this code, an HTML text result (string) is to be inserted. This text is typically generated by calling Flask's render_template function, which uses templates/view_results.html to turn the return object result from the compute function into the desired HTML code:

def index():
    ...
    if result:
        result = render_template('view_results.html', result=result)
        # result is now rendered HTML text
    return render_template('view.html', form=form, result=result)

Notice. A perhaps simpler alternative would be to have a generic view_forms.html file and a user-specific view_results.html and explicitly combining them into a new file. This requires file writing by the app, which one normally wants to avoid. Especially if the web app gets multiple users, the file writing may lead to corrupt files.

The complete, generic form of the index function becomes

def index():
    form = InputForm(request.form)
    if request.method == 'POST' and form.validate():
        arg_names = inspect.getargspec(compute).args
        kwargs = {name: getattr(form, name).data
                  for name in arg_names if hasattr(form, name)}
        result = compute(**kwargs)
    else:
        result = None
    if result:
        # result must be transformed to HTML and inserted as a
        # string in the generic view.html file
        result = render_template('view_results.html', result=result)
    return render_template('view.html', form=form, result=result)

if __name__ == '__main__':
    app.run(debug=True)

Application

Let us apply the files above to plot the gamma probability density function $$ g(x; a, h, A) = \frac{|h|}{\Gamma(a)A}\left(\frac{x}{A}\right)^{ah-1} e^{-\left(\frac{x}{A}\right)^h}, $$ and its cumulative density $$ G(x; a, h, A) = \int_0^x g(\tau; a, h, A)d\tau,$$ computed by numerically the Trapezoidal rule, for instance. We also want to compute and display the mean value $ A\Gamma(a + 1/h)/\Gamma(a) $ and standard deviation $$ \sigma = \frac{A}{\Gamma(a)}\sqrt{\Gamma(a + 2/h)\Gamma(a) - \Gamma(a+1/h)^2}.$$ Here, $ \Gamma(a) $ is the gamma function, which can be computed by math.gamma(a) in Python. Below is a compute.py file with the relevant implementations of $ g(x;a,h,A) $ (gamma_density), $ G(x; a, h, A) $ (gamma_cumulative), and a function compute_gamma for making a plot of $ g $ og $ G $ for $ x\in [0,7\sigma] $.

def gamma_density(x, a, h, A):
    # http://en.wikipedia.org/wiki/Gamma_distribution
    xA = x/float(A)
    return abs(h)/(math.gamma(a)*A)*(xA)**(a*h-1)*exp(-xA**h)

def gamma_cumulative(x, a, h, A):
    # Integrate gamma_density using the Trapezoidal rule.
    # Assume x is array.
    g = gamma_density(x, a, h, A)
    r = zeros_like(x)
    for i in range(len(r)-1):
        r[i+1] = r[i] + 0.5*(g[i] + g[i+1])*(x[i+1] - x[i])
    return r

def compute_gamma(a=0.5, h=2.0, A=math.sqrt(2), resolution=500):
    """Return plot and mean/st.dev. value of the gamma density."""
    gah = math.gamma(a + 1./h)
    mean = A*gah/math.gamma(a)
    stdev = A/math.gamma(a)*math.sqrt(
        math.gamma(a + 2./h)*math.gamma(a) - gah**2)
    x = linspace(0, 7*stdev, resolution+1)
    y = gamma_density(x, a, h, A)
    plt.figure()  # needed to avoid adding curves in plot
    plt.plot(x, y)
    plt.title('a=%g, h=%g, A=%g' % (a, h, A))
    # Make Matplotlib write to BytesIO file object and grab
    # return the object's string
    from io import BytesIO
    figfile = BytesIO()
    plt.savefig(figfile, format='png')
    figfile.seek(0)  # rewind to beginning of file
    import base64
    figdata_density_png = base64.b64encode(figfile.getvalue())
    figfile = BytesIO()
    plt.savefig(figfile, format='svg')
    figfile.seek(0)
    figdata_density_svg = '<svg' + figfile.getvalue().split('<svg')[1]
    figdata_density_svg = unicode(figdata_density_svg,'utf-8')

    y = gamma_cumulative(x, a, h, A)
    plt.figure()
    plt.plot(x, y)
    plt.grid(True)
    figfile = BytesIO()
    plt.savefig(figfile, format='png')
    figfile.seek(0)
    figdata_cumulative_png = base64.b64encode(figfile.getvalue())
    figfile = BytesIO()
    plt.savefig(figfile, format='svg')
    figfile.seek(0)
    figdata_cumulative_svg = '<svg' + figfile.getvalue().split('<svg')[1]
    figdata_cumulative_svg = unicode(figdata_cumulative_svg,'utf-8')
    return figdata_density_png, figdata_cumulative_png, \ 
           figdata_density_svg, figdata_cumulative_svg, \ 
           '%.2f' % mean, '%.2f' % stdev

The compute_gamma function returns a tuple of six values. We want output as displayed in Figure 10.

Figure 10: Design of a web page illustrating the gamma probability functions.

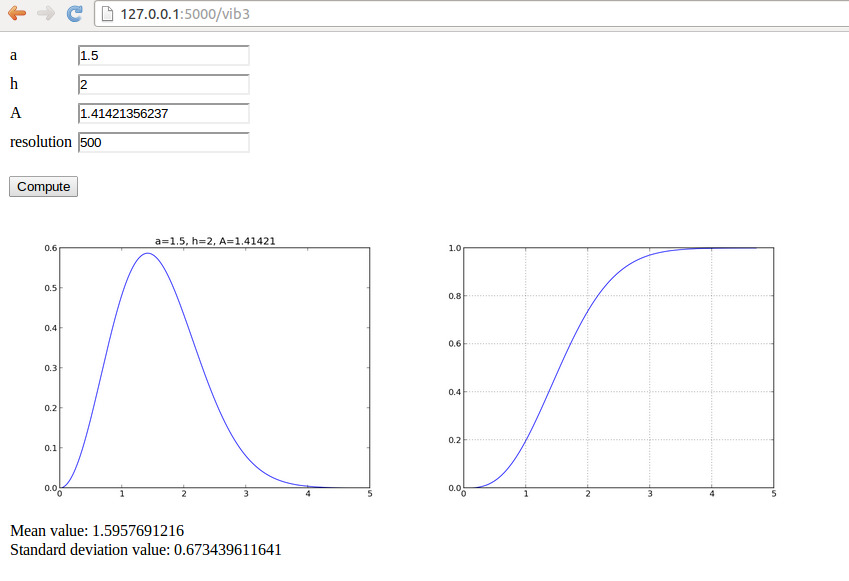
The design is realized in the file view_results.html shown below.

<p>
<table>
<tr>
<td>
<img src="data:image/png;base64,{{ result[0] }}" width="400">
</td><td>
<img src="data:image/png;base64,{{ result[1] }}" width="400">
</td></tr>
<tr>
<td>{{ result[2]|safe }}</td>
<td>{{ result[3]|safe }}</td>
</tr>
<tr><td>
Mean value: {{ result[4] }} <br>
Standard deviation value: {{ result[5] }}
</td></tr>
</table>
</p>

To create the web application, we just perform the following steps:

copy the generic controller.py and model.py files to a new directory
write the compute function in a file compute.py
edit controller.py and model.py to use the right name of the compute function (from compute import name as compute)
add an appropriate templates/view_forms.html file that visualizes the returned value results from the compute function