App. A: Sequences and difference equations
Aug 21, 2016
Sequences
Sequences is a central topic in mathematics:
$$ x_0,\ x_1,\ x_2,\ \ldots,\ x_n,\ldots, $$
Example: all odd numbers
$$ 1, 3, 5, 7, \ldots, 2n+1,\ldots $$
For this sequence we have a formula for the \( n \)-th term:
$$ x_n = 2n+1 $$
and we can write the sequence more compactly as
$$ (x_n)_{n=0}^\infty,\quad x_n = 2n+1$$
Other examples of sequences
$$ 1,\ 4,\ 9,\ 16,\ 25,\ \ldots\quad (x_n)_{n=0}^\infty,\ x_n=n^2$$
$$ 1,\ {1\over 2},\ {1\over3},\ {1\over4},\ \ldots\quad (x_n)_{n=0}^\infty,\ x_n={1\over {n+1}}$$
$$ 1,\ 1,\ 2,\ 6,\ 24,\ \ldots\quad (x_n)_{n=0}^\infty,\ x_n=n!$$
$$ 1,\ 1+x,\ 1+x+{1\over2}x^2,\ 1+x+{1\over2}x^2+{1\over6}x^3,\ \ldots\quad (x_n)_{n=0}^\infty,\ x_n=\sum_{j=0}^n {x^j\over j!}$$
Finite and infinite sequences
- Infinite sequences have an infinite number of terms (\( n\rightarrow\infty \))
- In mathematics, infinite sequences are widely used
- In real-life applications, sequences are usually finite: \( (x_n)_{n=0}^N \)
- Example: number of approved exercises every week in INF1100
\( x_0, x_1, x_2, \ldots, x_{15} \) - Example: the annual value of a loan
\( x_0, x_1, \ldots, x_{20} \)
Difference equations
- For sequences occuring in modeling of real-world phenomena, there is seldom a formula for the \( n \)-th term
- However, we can often set up one or more equations governing the sequence
- Such equations are called difference equations
- With a computer it is then very easy to generate the sequence by solving the difference equations
- Difference equations have lots of applications and are very easy to solve on a computer, but often complicated or impossible to solve for \( x_n \) (as a formula) by pen and paper!
- The programs require only loops and arrays
Modeling interest rates
Put \( x_0 \) money in a bank at year 0. What is the value after \( N \) years if the interest rate is \( p \) percent per year?
The fundamental information relates the value at year \( n \), \( x_n \), to the value of the previous year, \( x_{n-1} \):
$$ x_{n} = x_{n-1} + {p\over 100}x_{n-1} $$
How to solve for \( x_n \)? Start with \( x_0 \), compute \( x_1 \), \( x_2 \), ...
Simulating the difference equation for interest rates
Solve math equations by repeating a simple procedure (relation) many times (boring, but well suited for a computer!)
from scitools.std import *
x0 = 100 # initial amount
p = 5 # interest rate
N = 4 # number of years
index_set = range(N+1)
x = zeros(len(index_set))
# Solution:
x[0] = x0
for n in index_set[1:]:
x[n] = x[n-1] + (p/100.0)*x[n-1]
print x
plot(index_set, x, 'ro', xlabel='years', ylabel='amount')
We do not need to store the entire sequence, but it is convenient for programming and later plotting
- Previous program stores all the \( x_n \) values in a NumPy array
- To compute \( x_n \), we only need one previous value, \( x_{n-1} \)
Thus, we could only store the two last values in memory:
x_old = x0
for n in index_set[1:]:
x_new = x_old + (p/100.)*x_old
x_old = x_new # x_new becomes x_old at next step
However, programming with an array x[n] is simpler, safer, and enables plotting the sequence, so we will continue to use arrays in the examples
Daily interest rate
- A more relevant model is to add the interest every day
- The interest rate per day is \( r=p/D \) if \( p \) is the annual interest rate and \( D \) is the number of days in a year
- A common model in business applies \( D=360 \), but \( n \) counts exact (all) days
Just a minor change in the model:
$$x_{n} = x_{n-1} + {r\over 100}x_{n-1}$$
How can we find the number of days between two dates?
>>> import datetime
>>> date1 = datetime.date(2007, 8, 3) # Aug 3, 2007
>>> date2 = datetime.date(2008, 8, 4) # Aug 4, 2008
>>> diff = date2 - date1
>>> print diff.days
367
Program for daily interest rate
from scitools.std import *
x0 = 100 # initial amount
p = 5 # annual interest rate
r = p/360.0 # daily interest rate
import datetime
date1 = datetime.date(2007, 8, 3)
date2 = datetime.date(2011, 8, 3)
diff = date2 - date1
N = diff.days
index_set = range(N+1)
x = zeros(len(index_set))
# Solution:
x[0] = x0
for n in index_set[1:]:
x[n] = x[n-1] + (r/100.0)*x[n-1]
print x
plot(index_set, x, 'ro', xlabel='days', ylabel='amount')
But the annual interest rate may change quite often...
- Could not be handled in school (cannot apply \( x_n =x_0(1+\frac{p}{100})^n \))
- A varying \( p \) causes no problems in the program:
just fill an array
pwith correct interest rate for dayn
Modified program:
p = zeros(len(index_set))
# fill p[n] for n in index_set (might be non-trivial...)
r = p/360.0 # daily interest rate
x = zeros(len(index_set))
x[0] = x0
for n in index_set[1:]:
x[n] = x[n-1] + (r[n-1]/100.0)*x[n-1]
Payback of a loan
- A loan \( L \) is paid back with a fixed amount \( L/N \) every month over \( N \) months + the interest rate of the loan
- \( p \): annual interest rate, \( p/12: \) monthly rate
- Let \( x_n \) be the value of the loan at the end of month \( n \)
The fundamental relation from one month to the text:
$$ x_n = x_{n-1} + {p\over 12\cdot 100}x_{n-1} -
({p\over 12\cdot 100}x_{n-1} + {L\over N})$$
which simplifies to
$$ x_n = x_{n-1} - {L\over N}$$
(\( L/N \) makes the equation nonhomogeneous)
How to make a living from a fortune with constant consumption
- We have a fortune \( F \) invested with an annual interest rate of \( p \) percent
- Every year we plan to consume an amount \( c_n \) (\( n \) counts years)
- Let \( x_n \) be our fortune at year \( n \)
A fundamental relation from one year to the other is
$$ x_n = x_{n-1} + {p\over 100}x_{n-1} - c_n $$
Simplest possibility: keep \( c_n \) constant, but inflation demands \( c_n \) to increase...
How to make a living from a fortune with inflation-adjusted consumption
- Assume \( I \) percent inflation per year
- Start with \( c_0 \) as \( q \) percent of the interest the first year
- \( c_n \) then develops as money with interest rate \( I \)
\( x_n \) develops with rate \( p \) but with a loss \( c_n \) every year:
$$
\begin{align*}
x_n &= x_{n-1} + {p\over 100}x_{n-1} - c_{n-1}, \quad x_0=F,\ c_0 = {pq\over 10^4}F\\
c_n &= c_{n-1} + {I\over100}c_{n-1}
\end{align*}
$$
This is a coupled system of two difference equations, but the programming
is still simple: we update two arrays, first x[n], then c[n], inside the loop
(good exercise!)
The mathematics of Fibonacci numbers
No programming or math course is complete without an example on Fibonacci numbers:
$$ x_n = x_{n-1} + x_{n-2},\quad x_0=1,\ x_1=1$$
This is a homogeneous difference equation of second order (second order means three levels: \( n \), \( n-1 \), \( n-2 \)). This classification is important for mathematical solution technique, but not for simulation in a program.
Fibonacci derived the sequence by modeling rat populations, but the sequence of numbers has a range of peculiar mathematical properties and has therefore attracted much attention from mathematicians.
Program for generating Fibonacci numbers
N = int(sys.argv[1])
from numpy import zeros
x = zeros(N+1, int)
x[0] = 1
x[1] = 1
for n in range(2, N+1):
x[n] = x[n-1] + x[n-2]
print n, x[n]
Fibonacci numbers can cause overflow in NumPy arrays
Run the program with \( N=50 \):
2 2
3 3
4 5
5 8
6 13
...
45 1836311903
Warning: overflow encountered in long_scalars
46 -1323752223
Note:
- Changing
inttolongorint64for array elements allows \( N\leq 91 \) - Can use
float96(though \( x_n \) is integer): \( N \leq 23600 \)
No overflow when using Python int types
- Best: use Python scalars of type
int- these automatically changes tolongwhen overflow inint - The
longtype in Python has arbitrarily many digits (as many as required in a computation!) - Note:
longfor arrays is 64-bit integer (int64), while scalarlongin Python is an integer with as "infinitely" many digits
Program with Python's int type for integers
The program now avoids arrays and makes use of three int objects (which automatically changes to long when needed):
import sys
N = int(sys.argv[1])
xnm1 = 1 # "x_n minus 1"
xnm2 = 1 # "x_n minus 2"
n = 2
while n <= N:
xn = xnm1 + xnm2
print 'x_%d = %d' % (n, xn)
xnm2 = xnm1
xnm1 = xn
n += 1
Run with \( N=200 \):
x_2 = 2
x_3 = 3
...
x_198 = 173402521172797813159685037284371942044301
x_199 = 280571172992510140037611932413038677189525
x_200 = 453973694165307953197296969697410619233826
Limition: your computer's memory
New problem setting: exponential growth with limited environmental resources
The model for growth of money in a bank has a solution of the type
$$ x_n = x_0C^n \quad (= x_0e^{n\ln C})$$
Note:
- This is exponential growth in time (\( n \))
- Populations of humans, animals, and cells also exhibit the same type of growth as long as there are unlimited resources (space and food)
- Most environments can only support a maximum number \( M \) of individuals
- How can we model this limitation?
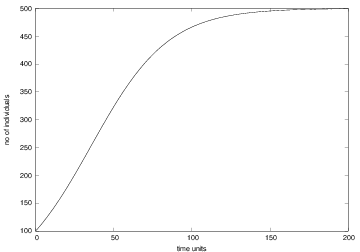
Modeling growth in an environment with limited resources
Initially, when there are enough resources, the growth is exponential:
$$ x_n = x_{n-1} + {r\over 100}x_{n-1}$$
The growth rate \( r \) must decay to zero as \( x_n \) approaches \( M \). The simplest variation of \( r(n) \) is a linear:
$$ r(n) = \varrho \left(1 - {x_n\over M}\right) $$
Observe: \( r(n)\approx \varrho \) for small \( n \) when \( x_n\ll M \), and \( r(n) \rightarrow 0 \) as \( x_n\rightarrow M \) and \( n \) is big
$$ x_n = x_{n-1} + {\varrho\over 100} x_{n-1}\left(1 - {x_{n-1}\over M}\right)$$
(This is a nonlinear difference equation)
The evolution of logistic growth
In a program it is easy to introduce logistic instead of exponential growth, just replace
x[n] = x[n-1] + p/100.0)*x[n-1]
by
x[n] = x[n-1] + (rho/100.0)*x[n-1]*(1 - x[n-1]/float(M))
The factorial as a difference equation
The factorial \( n! \) is defined as
$$ n(n-1)(n-2)\cdots 1,\quad 0!=1$$
The following difference equation has \( x_n=n! \) as solution and can be used to compute the factorial:
$$ x_n = nx_{n-1},\quad x_0 = 1 $$
Difference equations must have an initial condition
- In mathematics, it is much stressed that a difference equation for \( x_n \) must have an initial condition \( x_0 \)
- The initial condition is obvious when programming: otherwise we cannot start the program (\( x_0 \) is needed to compute \( x_n \))
- However: if you forget
x[0] = x0in the program, you get \( x_0=0 \) (becausex = zeroes(N+1)), which (usually) gives unintended results!
Have you ever though about how \( \sin x \) is really calculated?
- How can you calculate \( \sin x \), \( \ln x \), \( e^x \) without a calculator or program?
- These functions were originally defined to have some desired mathematical properties, but without an algorithm for how to evaluate function values
- Idea: approximate \( \sin x \), etc. by polynomials, since they are easy to calculate (sum, multiplication), but how??
Would you expect these fantastic mathematical results?
$$ \sin x = \sum_{k=0}^\infty (-1)^k\frac{x^{2k+1}}{(2k+1)!}$$
$$ f(x) = \sum_{k=0}^\infty \frac{1}{k!}(\frac{d^k}{dx^k} f(0))x^k $$
For "any" \( f(x) \), if we can differentiate, add, and multiply \( x^k \),
we can evaluate \( f \) at any \( x \) (!!!)
Taylor polynomials
$$ f(x) \approx \sum_{k=0}^{{\color{red} N}}
\frac{1}{k!}(\frac{d^k}{dx^k} f(0))x^k $$
\( N=1 \) is very popular and has been essential in developing physics and technology
$$
\begin{align*}
e^x &= \sum_{k=0}^\infty \frac{x^k}{k!}\\
&\approx 1 + x + \frac{1}{2}x^2 + \frac{1}{6}x^3\\
&\approx 1 + x
\end{align*}
$$
Taylor polynomials around an arbitrary point
The previous Taylor polynomials are most accurate around \( x=0 \). Can make the polynomials accurate around any point \( x=a \):
$$ f(x) \approx \sum_{k=0}^N \frac{1}{k!}(\frac{d^k}{dx^k} f(a))(x-a)^k $$
Taylor polynomial as one difference equation
The Taylor series for \( e^x \) around \( x=0 \) reads
$$ e^x= \sum_{n=0}^\infty {x^n\over n!} $$
Define
$$ e_{n}=\sum_{k=0}^{n-1} \frac{x^k}{k!} =
\sum_{k=0}^{n-2} \frac{x^k}{k!} + \frac{x^{n-1}}{(n-1)!}$$
We can formulate the sum in \( e_n \) as the following difference equation:
$$ e_n = e_{n-1} + \frac{x^{n-1}}{(n-1)!},\quad e_0=0 $$
More efficient computation: the Taylor polynomial as two difference equations
Observe:
$$ \frac{x^n}{n!} = \frac{x^{n-1}}{(n-1)!}\cdot \frac{x}{n} $$
Let \( a_n = x^n/n! \). Then we can efficiently compute \( a_n \) via
$$ a_n = a_{n-1}\frac{x}{n},\quad a_0 = 1$$
Now we can update each term via the \( a_n \) equation and sum the terms via the \( e_n \) equation:
$$
\begin{align*}
e_n &= e_{n-1} + a_{n-1},\quad e_0 = 0,\ a_0 = 1\\
a_n &= \frac{x}{n} a_{n-1}
\end{align*}
$$
See the book for more details
Nonlinear algebraic equations
\[ f(x)=0 \]
\[ ax + b = 0 \] \[ ax^2 + bx + c = 0 \] \[ \sin x + \cos x = 1 \]
- Simple numerical algorithms can solve "any" equation \( f(x)=0 \)
- Safest: Bisection
- Fastest: Newton's method
- Don't like \( f'(x) \) in Newton's method? Use the Secant method
- Secant and Newton are difference equations!
Newton's method for finding zeros; illustration
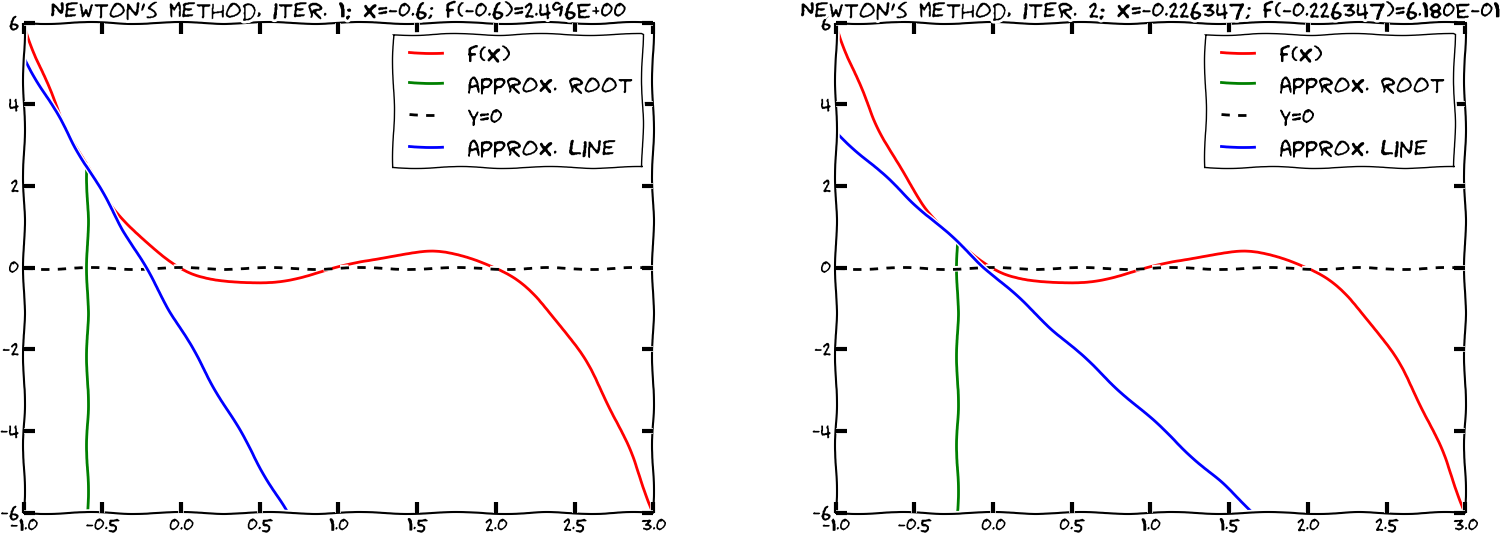
Newton's method for finding zeros; mathematics
Simpson (1740) came up with the following general method for solving \( f(x)=0 \) (based on ideas by Newton):
$$
x_n = x_{n-1} - {f(x_{n-1})\over f'(x_{n-1})},\quad x_0 \hbox{ given}
$$
Note:
- This is a (nonlinear!) difference equation
- As \( n\rightarrow\infty \), we hope that \( x_n\rightarrow x_s \), where \( x_s \) solves \( f(x_s)=0 \)
- How to choose \( N \) when what we want is \( x_N \) close to \( x_s \)?
- Need a slightly different program: simulate until \( f(x)\leq \epsilon \), where \( \epsilon \) is a small tolerance
- Caution: Newton's method may (easily) diverge, so \( f(x)\leq\epsilon \) may never occur!
A program for Newton's method
def Newton(f, x, dfdx, epsilon=1.0E-7, max_n=100):
n = 0
while abs(f(x)) > epsilon and n <= max_n:
x = x - f(x)/dfdx(x)
n += 1
return x, n, f(x)
Note:
- \( f(x) \) is evaluated twice in each pass of the loop - only one evaluation is strictly necessary (can store the value in a variable and reuse it)
-
f(x)/dfdx(x)can give integer division - It could be handy to store the
xandf(x)values in each iteration (for plotting or printing a convergence table)
An improved function for Newton's method
Only one \( f(x) \) call in each iteration, optional storage of \( (x,f(x)) \) values during the iterations, and ensured float division:
def Newton(f, x, dfdx, epsilon=1.0E-7, max_n=100,
store=False):
f_value = f(x)
n = 0
if store: info = [(x, f_value)]
while abs(f_value) > epsilon and n <= max_n:
x = x - float(f_value)/dfdx(x)
n += 1
f_value = f(x)
if store: info.append((x, f_value))
if store:
return x, info
else:
return x, n, f_value
Application of Newton's method
from math import sin, cos, exp, pi
import sys
def g(x):
return exp(-0.1*x**2)*sin(pi/2*x)
def dg(x):
return -2*0.1*x*exp(-0.1*x**2)*sin(pi/2*x) + \
pi/2*exp(-0.1*x**2)*cos(pi/2*x)
x0 = float(sys.argv[1])
x, info = Newton(g, x0, dg, store=True)
print 'Computed zero:', x
# Print the evolution of the difference equation
# (i.e., the search for the root)
for i in range(len(info)):
print 'Iteration %3d: f(%g)=%g' % (i, info[i][0], info[i][1])
Results from this test problem
\( x_0=1.7 \) gives quick convergence towards the closest root \( x=0 \):
zero: 1.999999999768449
Iteration 0: f(1.7)=0.340044
Iteration 1: f(1.99215)=0.00828786
Iteration 2: f(1.99998)=2.53347e-05
Iteration 3: f(2)=2.43808e-10
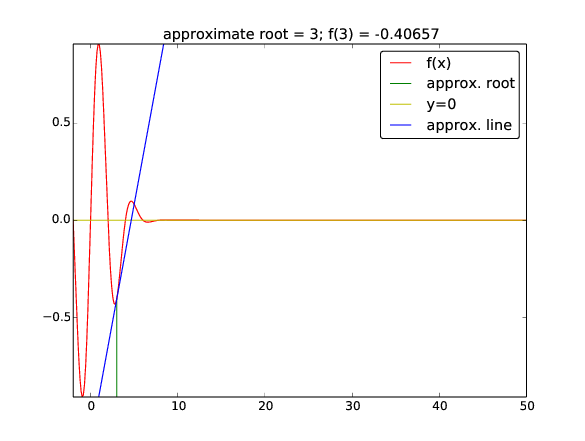
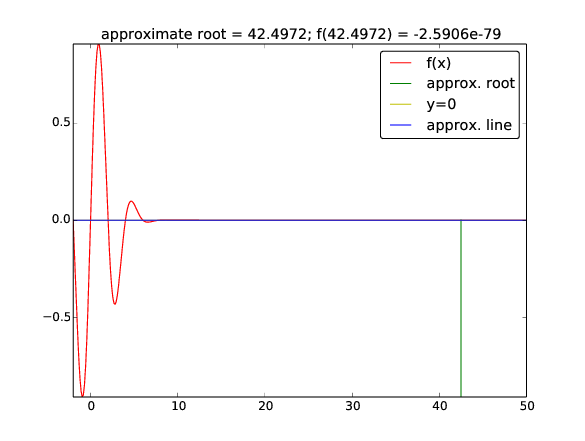
Start value \( x_0=3 \) (closest root \( x=2 \) or \( x=4 \)):
zero: 42.49723316011362
Iteration 0: f(3)=-0.40657
Iteration 1: f(4.66667)=0.0981146
Iteration 2: f(42.4972)=-2.59037e-79
What happened here??
Try the demo program src/diffeq/Newton_movie.py with \( x_0=3 \),
\( x\in [-2,50] \) for plotting and numerical approximation of \( f'(x) \):
Terminal> python Newton_movie.py "exp(-0.1*x**2)*sin(pi/2*x)" \
numeric 3 -2 50
Newton's method may work fine or give wrong results! You need to understand the method to interpret the results!
First step: we're moving to the right (\( x=4 \)?)
Second step: oops, too much to the right...
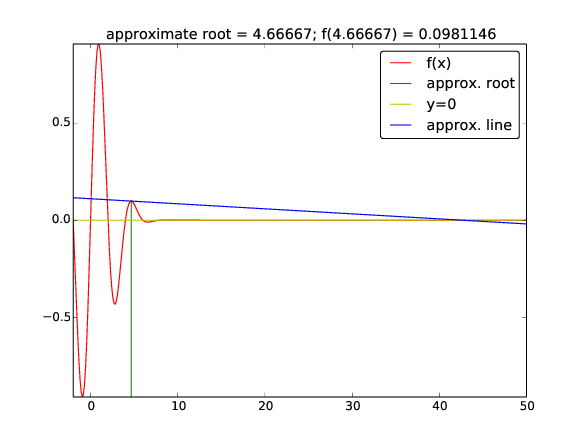
Third step: disaster since we're "done" (\( f(x)\approx 0 \))
Programming with sound
A tone A (440 Hz) is a sine wave with frequency 440 Hz:
$$ s(t) = A\sin\left( 2\pi f t\right),\quad f = 440 $$
On a computer we represent \( s(t) \) by a discrete set of points on the function curve (exactly as we do when we plot \( s(t) \)). CD quality needs 44100 samples per second.
Making a sound file with single tone (part 1)
- \( r \): sampling rate (samples per second, default 44100)
- \( f \): frequency of the tone
- \( m \): duration of the tone (seconds)
Sampled sine function for this tone:
$$ s_n =
A\sin\left( 2\pi f {n\over r}\right),
\quad n=0,1,\ldots, m\cdot r
$$
Code (we use descriptive names: frequency \( f \), length \( m \), amplitude \( A \), sample_rate \( r \)):
import numpy
def note(frequency, length, amplitude=1,
sample_rate=44100):
time_points = numpy.linspace(0, length,
length*sample_rate)
data = numpy.sin(2*numpy.pi*frequency*time_points)
data = amplitude*data
return data
Making a sound file with single tone (part 2)
- We have
dataas an array withfloatand unit amplitude - Sound data in a file should have 2-byte integers (
int16) as data elements and amplitudes up to \( 2^{15}-1 \) (max value forint16data)
data = note(440, 2)
data = data.astype(numpy.int16)
max_amplitude = 2**15 - 1
data = max_amplitude*data
import scitools.sound
scitools.sound.write(data, 'Atone.wav')
scitools.sound.play('Atone.wav')
Reading sound from file
- Let us read a sound file and add echo
- Sound = array
s[n] - Echo means to add a delay of the sound
# echo: e[n] = beta*s[n] + (1-beta)*s[n-b]
def add_echo(data, beta=0.8, delay=0.002,
sample_rate=44100):
newdata = data.copy()
shift = int(delay*sample_rate) # b (math symbol)
for i in xrange(shift, len(data)):
newdata[i] = beta*data[i] + (1-beta)*data[i-shift]
return newdata
Load data, add echo and play:
data = scitools.sound.read(filename)
data = data.astype(float)
data = add_echo(data, beta=0.6)
data = data.astype(int16)
scitools.sound.play(data)
Playing many notes
- Each note is an array of samples from a sine with a frequency corresponding to the note
- Assume we have several note arrays
data1,data2, ...:
# put data1, data2, ... after each other in a new array:
data = numpy.concatenate((data1, data2, data3, ...))
The start of "Nothing Else Matters" (Metallica):
E1 = note(164.81, .5)
G = note(392, .5)
B = note(493.88, .5)
E2 = note(659.26, .5)
intro = numpy.concatenate((E1, G, B, E2, B, G))
...
song = numpy.concatenate((intro, intro, ...))
scitools.sound.play(song)
scitools.sound.write(song, 'tmp.wav')
Summary of difference equations
- Sequence: \( x_0 \), \( x_1 \), \( x_2 \), \( \ldots \), \( x_n \), \( \ldots \), \( x_N \)
- Difference equation: relation between \( x_n \), \( x_{n-1} \) and maybe \( x_{n-2} \) (or more terms in the "past") + known start value \( x_0 \) (and more values \( x_1 \), ... if more levels enter the equation)
Solution of difference equations by simulation:
index_set = <array of n-values: 0, 1, ..., N>
x = zeros(N+1)
x[0] = x0
for n in index_set[1:]:
x[n] = <formula involving x[n-1]>
Can have (simple) systems of difference equations:
for n in index_set[1:]:
x[n] = <formula involving x[n-1]>
y[n] = <formula involving y[n-1] and x[n]>
Taylor series and numerical methods such as Newton's method can be formulated as difference equations, often resulting in a good way of programming the formulas
Summarizing example: music of sequences
- Given a \( x_0 \), \( x_1 \), \( x_2 \), \( \ldots \), \( x_n \), \( \ldots \), \( x_N \)
- Can we listen to this sequence as "music"?
- Yes, we just transform the \( x_n \) values to suitable frequencies and use the functions in
scitools.soundto generate tones
We will study two sequences:
$$ x_n = e^{-4n/N}\sin(8\pi n/N)$$
and
$$ x_n = x_{n-1} + q x_{n-1}\left(1 - x_{n-1}\right),\quad x = x_0 $$
The first has values in \( [-1,1] \), the other from \( x_0=0.01 \) up to around 1
Transformation from "unit" \( x_n \) to frequencies:
$$ y_n = 440 + 200 x_n $$
(first sequence then gives tones between 240 Hz and 640 Hz)
Module file: soundeq.py
- Three functions: two for generating sequences, one for the sound
- Look at
files/soundeq.pyfor complete code
Try it out in these examples:
Terminal> python soundseq.py oscillations 40
Terminal> python soundseq.py logistic 100
Try to change the frequency range from 200 to 400.