

float, list, file, ...)
Consider a function of \( t \) with a parameter \( v_0 \): $$ y(t; v_0)=v_0t - {1\over2}gt^2$$
We need both \( v_0 \) and \( t \) to evaluate \( y \) (and \( g=9.81 \)), but how should we implement this?
def y(t, v0):
g = 9.81
return v0*t - 0.5*g*t**2
def y(t):
g = 9.81
return v0*t - 0.5*g*t**2
Motivation: \( y(t) \) is a function of \( t \) only
y(t) can be a function of t only, but still havev0 and g as parameters with given values.
y(t) and data (v0, g)
Y for \( y(t;v_0) \) with variables v0 and g
and a function value(t) for computing \( y(t;v_0) \)__init__ for initialization of the variables

class Y:
def __init__(self, v0):
self.v0 = v0
self.g = 9.81
def value(self, t):
return self.v0*t - 0.5*self.g*t**2
Usage:
y = Y(v0=3) # create instance (object)
v = y.value(0.1) # compute function value
When we write
y = Y(v0=3)
we create a new variable (instance) y of type Y.
Y(3) is a call to the constructor:
def __init__(self, v0):
self.v0 = v0
self.g = 9.81
self variable? Stay cool - it will be understood later as you get used to it
self as y, i.e., the new variable to be created. self.v0 = ... means that we attach a variable v0 to self (y).Y(3) means Y.__init__(y, 3), i.e., set self=y, v0=3self is always first parameter in a function, but never inserted in the call!y = Y(3), y has two variables v0 and g
print y.v0
print y.g
In mathematics you don't understand things. You just get used to them. John von Neumann, mathematician, 1903-1957.
value method:
def value(self, t):
return self.v0*t - 0.5*self.g*t**2
Example on a call:
v = y.value(t=0.1)
self is left out in the call, but Python automatically inserts y as the self argument inside the value method. Think of the call as
Y.value(y, t=0.1)
Inside value things "appear" as
return y.v0*t - 0.5*y.g*t**2
self gives access to "global variables" in the class object.
Y collects the attributes v0 and g and the method value as one unitvalue(t) is function of t only, but has automatically access to the parameters v0 and g as self.v0 and self.gy.value as an ordinary function of t to any other function that expects a function f(t) of one variable
def make_table(f, tstop, n):
for t in linspace(0, tstop, n):
print t, f(t)
def g(t):
return sin(t)*exp(-t)
table(g, 2*pi, 101) # send ordinary function
y = Y(6.5)
table(y.value, 2*pi, 101) # send class method
Given a function with \( n+1 \) parameters and one independent variable,
$$ f(x; p_0,\ldots,p_n)$$
it is wise to represent f by a class where
\( p_0,\ldots,p_n \) are attributes and where there is a method, say value(self, x), for computing \( f(x) \)
class MyFunc:
def __init__(self, p0, p1, p2, ..., pn):
self.p0 = p0
self.p1 = p1
...
self.pn = pn
def value(self, x):
return ...
class VelocityProfile:
def __init__(self, beta, mu0, n, R):
self.beta, self.mu0, self.n, self.R = \
beta, mu0, n, R
def value(self, r):
beta, mu0, n, R = \
self.beta, self.mu0, self.n, self.R
n = float(n) # ensure float divisions
v = (beta/(2.0*mu0))**(1/n)*(n/(n+1))*\
(R**(1+1/n) - r**(1+1/n))
return v
v = VelocityProfile(R=1, beta=0.06, mu0=0.02, n=0.1)
print v.value(r=0.1)
class MyClass:
def __init__(self, p1, p2):
self.attr1 = p1
self.attr2 = p2
def method1(self, arg):
# can init new attribute outside constructor:
self.attr3 = arg
return self.attr1 + self.attr2 + self.attr3
def method2(self):
print 'Hello!'
m = MyClass(4, 10)
print m.method1(-2)
m.method2()
It is common to have a constructor where attributes are initialized, but this is not a requirement - attributes can be defined whenever desired
Y where there is no constructor (which is possible)
You have two choices:
self really isself until you have much more
experience with class programming (suddenly self becomes clear!)
The syntax
y = Y(3)
can be thought of as
Y.__init__(y, 3) # class prefix Y. is like a module prefix
Then
self.v0 = v0
is actually
y.v0 = 3
self works in the value method
v = y.value(2)
can alternatively be written as
v = Y.value(y, 2)
So, when we do instance.method(arg1, arg2), self becomes
instance inside method.
self
id(obj): print unique Python identifier of an object
class SelfExplorer:
"""Class for computing a*x."""
def __init__(self, a):
self.a = a
print 'init: a=%g, id(self)=%d' % (self.a, id(self))
def value(self, x):
print 'value: a=%g, id(self)=%d' % (self.a, id(self))
return self.a*x
>>> s1 = SelfExplorer(1)
init: a=1, id(self)=38085696
>>> id(s1)
38085696
>>> s2 = SelfExplorer(2)
init: a=2, id(self)=38085192
>>> id(s2)
38085192
>>> s1.value(4)
value: a=1, id(self)=38085696
4
>>> SelfExplorer.value(s1, 4)
value: a=1, id(self)=38085696
4
>>> s2.value(5)
value: a=2, id(self)=38085192
10
>>> SelfExplorer.value(s2, 5)
value: a=2, id(self)=38085192
10
You have two choices:
self really isself until you have much more
experience with class programming (suddenly self becomes clear!)
The syntax
y = Y(3)
can be thought of as
Y.__init__(y, 3) # class prefix Y. is like a module prefix
Then
self.v0 = v0
is actually
y.v0 = 3
self works in the value method
v = y.value(2)
can alternatively be written as
v = Y.value(y, 2)
So, when we do instance.method(arg1, arg2), self becomes
instance inside method.
self
id(obj): print unique Python identifier of an object
class SelfExplorer:
"""Class for computing a*x."""
def __init__(self, a):
self.a = a
print 'init: a=%g, id(self)=%d' % (self.a, id(self))
def value(self, x):
print 'value: a=%g, id(self)=%d' % (self.a, id(self))
return self.a*x
>>> s1 = SelfExplorer(1)
init: a=1, id(self)=38085696
>>> id(s1)
38085696
>>> s2 = SelfExplorer(2)
init: a=2, id(self)=38085192
>>> id(s2)
38085192
>>> s1.value(4)
value: a=1, id(self)=38085696
4
>>> SelfExplorer.value(s1, 4)
value: a=1, id(self)=38085696
4
>>> s2.value(5)
value: a=2, id(self)=38085192
10
>>> SelfExplorer.value(s2, 5)
value: a=2, id(self)=38085192
10
class Account:
def __init__(self, name, account_number, initial_amount):
self.name = name
self.no = account_number
self.balance = initial_amount
def deposit(self, amount):
self.balance += amount
def withdraw(self, amount):
self.balance -= amount
def dump(self):
s = '%s, %s, balance: %s' % \
(self.name, self.no, self.balance)
print s

>>> a1 = Account('John Olsson', '19371554951', 20000)
>>> a2 = Account('Liz Olsson', '19371564761', 20000)
>>> a1.deposit(1000)
>>> a1.withdraw(4000)
>>> a2.withdraw(10500)
>>> a1.withdraw(3500)
>>> print "a1's balance:", a1.balance
a1's balance: 13500
>>> a1.dump()
John Olsson, 19371554951, balance: 13500
>>> a2.dump()
Liz Olsson, 19371564761, balance: 9500
>>> a1.name = 'Some other name'
>>> a1.balance = 100000
>>> a1.no = '19371564768'
balance attribute can be viewedbalance is done through withdraw or deposit
Attributes and methods not intended for use outside the class can be marked as protected by prefixing the name with an underscore (e.g., _name). This is just a convention - and no technical way of avoiding attributes and methods to be accessed.
class AccountP:
def __init__(self, name, account_number, initial_amount):
self._name = name
self._no = account_number
self._balance = initial_amount
def deposit(self, amount):
self._balance += amount
def withdraw(self, amount):
self._balance -= amount
def get_balance(self): # NEW - read balance value
return self._balance
def dump(self):
s = '%s, %s, balance: %s' % \
(self._name, self._no, self._balance)
print s
a1 = AccountP('John Olsson', '19371554951', 20000)
a1.withdraw(4000)
print a1._balance # it works, but a convention is broken
print a1.get_balance() # correct way of viewing the balance
a1._no = '19371554955' # this is a "serious crime"!

class Person:
def __init__(self, name,
mobile_phone=None, office_phone=None,
private_phone=None, email=None):
self.name = name
self.mobile = mobile_phone
self.office = office_phone
self.private = private_phone
self.email = email
def add_mobile_phone(self, number):
self.mobile = number
def add_office_phone(self, number):
self.office = number
def add_private_phone(self, number):
self.private = number
def add_email(self, address):
self.email = address
class Person:
...
def dump(self):
s = self.name + '\n'
if self.mobile is not None:
s += 'mobile phone: %s\n' % self.mobile
if self.office is not None:
s += 'office phone: %s\n' % self.office
if self.private is not None:
s += 'private phone: %s\n' % self.private
if self.email is not None:
s += 'email address: %s\n' % self.email
print s
p1 = Person('Hans Petter Langtangen', email='hpl@simula.no')
p1.add_office_phone('67828283'),
p2 = Person('Aslak Tveito', office_phone='67828282')
p2.add_email('aslak@simula.no')
phone_book = [p1, p2] # list
phone_book = {'Langtangen': p1, 'Tveito': p2} # better
for p in phone_book:
p.dump()
area, circumference
class Circle:
def __init__(self, x0, y0, R):
self.x0, self.y0, self.R = x0, y0, R
def area(self):
return pi*self.R**2
def circumference(self):
return 2*pi*self.R
>>> c = Circle(2, -1, 5)
>>> print 'A circle with radius %g at (%g, %g) has area %g' % \
... (c.R, c.x0, c.y0, c.area())
A circle with radius 5 at (2, -1) has area 78.5398
def test_Circle():
R = 2.5
c = Circle(7.4, -8.1, R)
from math import pi
expected_area = pi*R**2
computed_area = c.area()
diff = abs(expected_area - computed_area)
tol = 1E-14
assert diff < tol, 'bug in Circle.area, diff=%s' % diff
expected_circumference = 2*pi*R
computed_circumference = c.circumference()
diff = abs(expected_circumference - computed_circumference)
assert diff < tol, 'bug in Circle.circumference, diff=%s' % diff
class MyClass:
def __init__(self, a, b):
...
p1 = MyClass(2, 5)
p2 = MyClass(-1, 10)
p3 = p1 + p2
p4 = p1 - p2
p5 = p1*p2
p6 = p1**7 + 4*p3
def __init__(self, ...)
def __call__(self, ...)
def __add__(self, other)
# Python syntax
y = Y(4)
print y(2)
z = Y(6)
print y + z
# What's actually going on
Y.__init__(y, 4)
print Y.__call__(y, 2)
Y.__init__(z, 6)
print Y.__add__(y, z)
We shall learn about many more such special methods
Replace the value method by a call special method:
class Y:
def __init__(self, v0):
self.v0 = v0
self.g = 9.81
def __call__(self, t):
return self.v0*t - 0.5*self.g*t**2
Now we can write
y = Y(3)
v = y(0.1) # same as v = y.__call__(0.1) or Y.__call__(y, 0.1)
Note:
y behaves and looks as a function!value(t) method does the same, but __call__ allows nicer syntax for computing function values
Given a function with \( n+1 \) parameters and one independent variable,
$$ f(x; p_0,\ldots,p_n)$$
it is wise to represent f by a class where \( p_0,\ldots,p_n \)
are attributes and __call__(x) computes \( f(x) \)
class MyFunc:
def __init__(self, p0, p1, p2, ..., pn):
self.p0 = p0
self.p1 = p1
...
self.pn = pn
def __call__(self, x):
return ...
Given some mathematical function in Python, say
def f(x):
return x**3
can we make a class Derivative and write
dfdx = Derivative(f)
so that dfdx behaves as a function that computes the derivative of f(x)?
print dfdx(2) # computes 3*x**2 for x=2
We use numerical differentiation "behind the curtain": $$ f'(x) \approx {f(x+h)-f(x)\over h} $$ for a small (yet moderate) \( h \), say \( h=10^{-5} \)
class Derivative:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
def __call__(self, x):
f, h = self.f, self.h # make short forms
return (f(x+h) - f(x))/h
>>> from math import *
>>> df = Derivative(sin)
>>> x = pi
>>> df(x)
-1.000000082740371
>>> cos(x) # exact
-1.0
>>> def g(t):
... return t**3
...
>>> dg = Derivative(g)
>>> t = 1
>>> dg(t) # compare with 3 (exact)
3.000000248221113
Newton's method solves nonlinear equations \( f(x)=0 \), but the method requires \( f'(x) \)
def Newton(f, xstart, dfdx, epsilon=1E-6):
...
return x, no_of_iterations, f(x)
Suppose \( f'(x) \) requires boring/lengthy derivation, then class Derivative is handy:
>>> def f(x):
... return 100000*(x - 0.9)**2 * (x - 1.1)**3
...
>>> df = Derivative(f)
>>> xstart = 1.01
>>> Newton(f, xstart, df, epsilon=1E-5)
(1.0987610068093443, 8, -7.5139644257961411e-06)
Derivative?
def test_Derivative():
# The formula is exact for linear functions, regardless of h
f = lambda x: a*x + b
a = 3.5; b = 8
dfdx = Derivative(f, h=0.5)
diff = abs(dfdx(4.5) - a)
assert diff < 1E-14, 'bug in class Derivative, diff=%s' % diff
f = lambda x: a*x + b
is equivalent to
def f(x):
return a*x + b
Lambda functions are convenient for producing quick, short code
f = lambda x: a*x + b
a = 3.5; b = 8
dfdx = Derivative(f, h=0.5)
dfdx(4.5)
Looks straightforward...but
Derivative.__call__ know a and b when it calls
our f(x) function?f can access a and b in test_Derivative even when
called from __call__ in class `Derivativef is known as a closure in computer science
SymPy can perform exact, symbolic differentiation:
>>> from sympy import *
>>> def g(t):
... return t**3
...
>>> t = Symbol('t')
>>> dgdt = diff(g(t), t) # compute g'(t)
>>> dgdt
3*t**2
>>> # Turn sympy expression dgdt into Python function dg(t)
>>> dg = lambdify([t], dgdt)
>>> dg(1)
3
import sympy as sp
class Derivative_sympy:
def __init__(self, f):
# f: Python f(x)
x = sp.Symbol('x')
sympy_f = f(x)
sympy_dfdx = sp.diff(sympy_f, x)
self.__call__ = sp.lambdify([x], sympy_dfdx)
>>> def g(t):
... return t**3
>>> def h(y):
... return sp.sin(y)
>>> dg = Derivative_sympy(g)
>>> dh = Derivative_sympy(h)
>>> dg(1) # 3*1**2 = 3
3
>>> from math import pi
>>> dh(pi) # cos(pi) = -1
-1.0
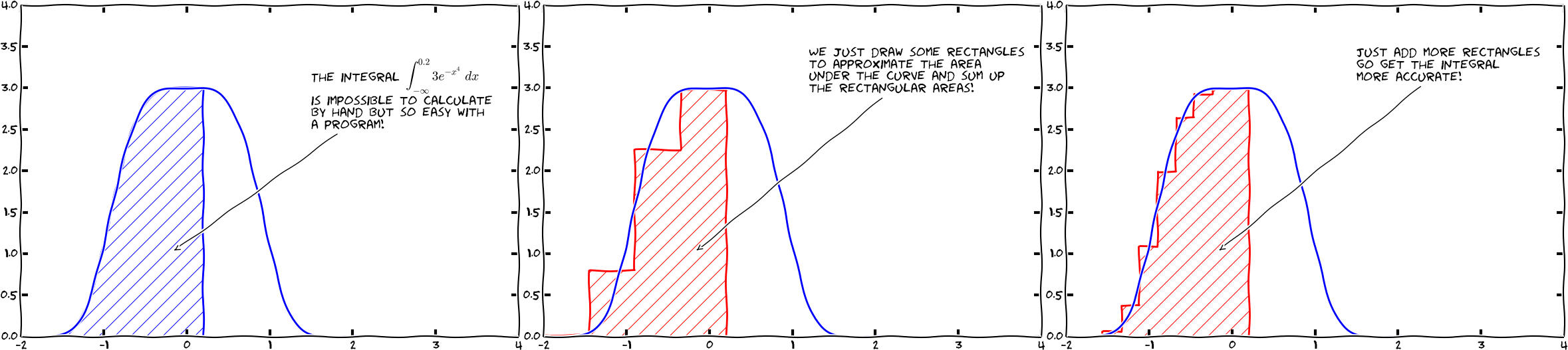
Given a function \( f(x) \), we want to compute $$ F(x; a) = \int_a^x f(t)dt $$
$$ F(x; a) = \int_a^x f(t)dt $$
Technique: Midpoint rule or Trapezoidal rule, here the latter: $$ \int_a^x f(t)dt = h\left({1\over2}f(a) + \sum_{i=1}^{n-1} f(a+ih) + {1\over2}f(x)\right) $$
Desired application code:
def f(x):
return exp(-x**2)*sin(10*x)
a = 0; n = 200
F = Integral(f, a, n)
x = 1.2
print F(x)
def trapezoidal(f, a, x, n):
h = (x-a)/float(n)
I = 0.5*f(a)
for i in range(1, n):
I += f(a + i*h)
I += 0.5*f(x)
I *= h
return I
Class Integral holds f, a and n as attributes and has a call special method for computing the integral:
class Integral:
def __init__(self, f, a, n=100):
self.f, self.a, self.n = f, a, n
def __call__(self, x):
return trapezoidal(self.f, self.a, x, self.n)
Integral?
def test_Integral():
f = lambda x: 2*x + 5
F = lambda x: x**2 + 5*x - (a**2 + 5*a)
a = 2
dfdx = Integralf, a, n=4)
x = 6
diff = abs(I(x) - (F(x) - F(a)))
assert diff < 1E-15, 'bug in class Integral, diff=%s' % diff
a by print a,
works for built-in types (strings, lists, floats, ...)__str__, Python will use this method to convert an object to a string
class Y:
...
def __call__(self, t):
return self.v0*t - 0.5*self.g*t**2
def __str__(self):
return 'v0*t - 0.5*g*t**2; v0=%g' % self.v0
Demo:
>>> y = Y(1.5)
>>> y(0.2)
0.1038
>>> print y
v0*t - 0.5*g*t**2; v0=1.5
A polynomial can be specified by a list of its coefficients. For example, \( 1 - x^2 + 2x^3 \) is $$ 1 + 0\cdot x - 1\cdot x^2 + 2\cdot x^3 $$
and the coefficients can be stored as [1, 0, -1, 2]
>>> p1 = Polynomial([1, -1])
>>> print p1
1 - x
>>> p2 = Polynomial([0, 1, 0, 0, -6, -1])
>>> p3 = p1 + p2
>>> print p3.coeff
[1, 0, 0, 0, -6, -1]
>>> print p3
1 - 6*x^4 - x^5
>>> p2.differentiate()
>>> print p2
1 - 24*x^3 - 5*x^4
How can we make class Polynomial?
class Polynomial:
def __init__(self, coefficients):
self.coeff = coefficients
def __call__(self, x):
s = 0
for i in range(len(self.coeff)):
s += self.coeff[i]*x**i
return s
class Polynomial:
...
def __add__(self, other):
# return self + other
# start with the longest list and add in the other:
if len(self.coeff) > len(other.coeff):
coeffsum = self.coeff[:] # copy!
for i in range(len(other.coeff)):
coeffsum[i] += other.coeff[i]
else:
coeffsum = other.coeff[:] # copy!
for i in range(len(self.coeff)):
coeffsum[i] += self.coeff[i]
return Polynomial(coeffsum)
Multiplication of two general polynomials: $$ \left(\sum_{i=0}^Mc_ix^i\right)\left(\sum_{j=0}^N d_jx^j\right) = \sum_{i=0}^M \sum_{j=0}^N c_id_j x^{i+j} $$
The coeff. corresponding to power \( i+j \) is \( c_i\cdot d_j \). The
list r of coefficients of the result:
r[i+j] = c[i]*d[j] (i and j running from
0 to \( M \) and \( N \), resp.)
class Polynomial:
...
def __mul__(self, other):
M = len(self.coeff) - 1
N = len(other.coeff) - 1
coeff = [0]*(M+N+1) # or zeros(M+N+1)
for i in range(0, M+1):
for j in range(0, N+1):
coeff[i+j] += self.coeff[i]*other.coeff[j]
return Polynomial(coeff)
Rule for differentiating a general polynomial: $$ {d\over dx}\sum_{i=0}^n c_ix^i = \sum_{i=1}^n ic_ix^{i-1}$$
If c is the list of coefficients, the derivative has a list
of coefficients, dc, where dc[i-1] = i*c[i] for
i running from 1 to the largest index in c.
Note that dc has one element less than c.
class Polynomial:
...
def differentiate(self): # change self
for i in range(1, len(self.coeff)):
self.coeff[i-1] = i*self.coeff[i]
del self.coeff[-1]
def derivative(self): # return new polynomial
dpdx = Polynomial(self.coeff[:]) # copy
dpdx.differentiate()
return dpdx
class Polynomial:
...
def __str__(self):
s = ''
for i in range(0, len(self.coeff)):
if self.coeff[i] != 0:
s += ' + %g*x^%d' % (self.coeff[i], i)
# fix layout (lots of special cases):
s = s.replace('+ -', '- ')
s = s.replace(' 1*', ' ')
s = s.replace('x^0', '1')
s = s.replace('x^1 ', 'x ')
s = s.replace('x^1', 'x')
if s[0:3] == ' + ': # remove initial +
s = s[3:]
if s[0:3] == ' - ': # fix spaces for initial -
s = '-' + s[3:]
return s
Consider $$ p_1(x)= 1-x,\quad p_2(x)=x - 6x^4 - x^5 $$ and their sum $$ p_3(x) = p_1(x) + p_2(x) = 1 -6x^4 - x^5 $$
>>> p1 = Polynomial([1, -1])
>>> print p1
1 - x
>>> p2 = Polynomial([0, 1, 0, 0, -6, -1])
>>> p3 = p1 + p2
>>> print p3.coeff
[1, 0, 0, 0, -6, -1]
>>> p2.differentiate()
>>> print p2
1 - 24*x^3 - 5*x^4
How should, e.g., __add__(self, other) be defined? This is completely up to the programmer, depending on what is meaningful by object1 + object2.
An anthropologist was asking a primitive tribesman about arithmetic. When the anthropologist asked, What does two and two make? the tribesman replied, Five. Asked to explain, the tribesman said, If I have a rope with two knots, and another rope with two knots, and I join the ropes together, then I have five knots.
c = a + b # c = a.__add__(b)
c = a - b # c = a.__sub__(b)
c = a*b # c = a.__mul__(b)
c = a/b # c = a.__div__(b)
c = a**e # c = a.__pow__(e)
a == b # a.__eq__(b)
a != b # a.__ne__(b)
a < b # a.__lt__(b)
a <= b # a.__le__(b)
a > b # a.__gt__(b)
a >= b # a.__ge__(b)
$$ \begin{align*} (a,b) + (c,d) &= (a+c, b+d)\\ (a,b) - (c,d) &= (a-c, b-d)\\ (a,b)\cdot(c,d) &= ac + bd\\ (a,b) &= (c, d)\hbox{ if }a=c\hbox{ and }b=d \end{align*} $$
>>> u = Vec2D(0,1)
>>> v = Vec2D(1,0)
>>> print u + v
(1, 1)
>>> a = u + v
>>> w = Vec2D(1,1)
>>> a == w
True
>>> print u - v
(-1, 1)
>>> print u*v
0
class Vec2D:
def __init__(self, x, y):
self.x = x; self.y = y
def __add__(self, other):
return Vec2D(self.x+other.x, self.y+other.y)
def __sub__(self, other):
return Vec2D(self.x-other.x, self.y-other.y)
def __mul__(self, other):
return self.x*other.x + self.y*other.y
def __abs__(self):
return math.sqrt(self.x**2 + self.y**2)
def __eq__(self, other):
return self.x == other.x and self.y == other.y
def __str__(self):
return '(%g, %g)' % (self.x, self.y)
def __ne__(self, other):
return not self.__eq__(other) # reuse __eq__
eval(repr(p)) creates p
class MyClass:
def __init__(self, a, b):
self.a, self.b = a, b
def __str__(self):
"""Return string with pretty print."""
return 'a=%s, b=%s' % (self.a, self.b)
def __repr__(self):
"""Return string such that eval(s) recreates self."""
return 'MyClass(%s, %s)' % (self.a, self.b)
>>> m = MyClass(1, 5)
>>> print m # calls m.__str__()
a=1, b=5
>>> str(m) # calls m.__str__()
'a=1, b=5'
>>> s = repr(m) # calls m.__repr__()
>>> s
'MyClass(1, 5)'
>>> m2 = eval(s) # same as m2 = MyClass(1, 5)
>>> m2 # calls m.__repr__()
'MyClass(1, 5)'
class Y:
"""Class for function y(t; v0, g) = v0*t - 0.5*g*t**2."""
def __init__(self, v0):
"""Store parameters."""
self.v0 = v0
self.g = 9.81
def __call__(self, t):
"""Evaluate function."""
return self.v0*t - 0.5*self.g*t**2
def __str__(self):
"""Pretty print."""
return 'v0*t - 0.5*g*t**2; v0=%g' % self.v0
def __repr__(self):
"""Print code for regenerating this instance."""
return 'Y(%s)' % self.v0
Python already has a class complex for complex numbers, but implementing such a class is a good pedagogical example on class programming (especially with special methods).
>>> u = Complex(2,-1)
>>> v = Complex(1) # zero imaginary part
>>> w = u + v
>>> print w
(3, -1)
>>> w != u
True
>>> u*v
Complex(2, -1)
>>> u < v
illegal operation "<" for complex numbers
>>> print w + 4
(7, -1)
>>> print 4 - w
(1, 1)
class Complex:
def __init__(self, real, imag=0.0):
self.real = real
self.imag = imag
def __add__(self, other):
return Complex(self.real + other.real,
self.imag + other.imag)
def __sub__(self, other):
return Complex(self.real - other.real,
self.imag - other.imag)
def __mul__(self, other):
return Complex(self.real*other.real - self.imag*other.imag,
self.imag*other.real + self.real*other.imag)
def __div__(self, other):
ar, ai, br, bi = self.real, self.imag, \
other.real, other.imag # short forms
r = float(br**2 + bi**2)
return Complex((ar*br+ai*bi)/r, (ai*br-ar*bi)/r)
def __abs__(self):
return sqrt(self.real**2 + self.imag**2)
def __neg__(self): # defines -c (c is Complex)
return Complex(-self.real, -self.imag)
def __eq__(self, other):
return self.real == other.real and \
self.imag == other.imag
def __ne__(self, other):
return not self.__eq__(other)
def __str__(self):
return '(%g, %g)' % (self.real, self.imag)
def __repr__(self):
return 'Complex' + str(self)
def __pow__(self, power):
raise NotImplementedError(
'self**power is not yet impl. for Complex')
Can we add a real number to a complex number?
>>> u = Complex(1, 2)
>>> w = u + 4.5
...
AttributeError: 'float' object has no attribute 'real'
Problem: we have assumed that other is Complex.
Remedy:
class Complex:
...
def __add__(self, other):
if isinstance(other, (float,int)):
other = Complex(other)
return Complex(self.real + other.real,
self.imag + other.imag)
# or
def __add__(self, other):
if isinstance(other, (float,int)):
return Complex(self.real + other, self.imag)
else:
return Complex(self.real + other.real,
self.imag + other.imag)
What if we try this:
>>> u = Complex(1, 2)
>>> w = 4.5 + u
...
TypeError: unsupported operand type(s) for +:
'float' and 'instance'
Problem: Python's float objects cannot add a Complex.
Remedy: if a class has an __radd__(self, other) special method, Python applies this for other + self
class Complex:
...
def __radd__(self, other):
"""Rturn other + self."""
# other + self = self + other:
return self.__add__(other)
Right operands for subtraction is a bit more complicated since \( a-b \neq b-a \):
class Complex:
...
def __sub__(self, other):
if isinstance(other, (float,int)):
other = Complex(other)
return Complex(self.real - other.real,
self.imag - other.imag)
def __rsub__(self, other):
if isinstance(other, (float,int)):
other = Complex(other)
return other.__sub__(self)
class A:
"""A class for demo purposes."""
def __init__(self, value):
self.v = value
Any instance holds its attributes in the self.__dict__ dictionary (Python automatically creates this dict)
>>> a = A([1,2])
>>> print a.__dict__ # all attributes
{'v': [1, 2]}
>>> dir(a) # what's in object a?
'__doc__', '__init__', '__module__', 'dump', 'v']
>>> a.__doc__ # programmer's documentation of A
'A class for demo purposes.'
>>> a.myvar = 10 # add new attribute (!)
>>> a.__dict__
{'myvar': 10, 'v': [1, 2]}
>>> dir(a)
['__doc__', '__init__', '__module__', 'dump', 'myvar', 'v']
>>> b = A(-1)
>>> b.__dict__ # b has no myvar attribute
{'v': -1}
>>> dir(b)
['__doc__', '__init__', '__module__', 'dump', 'v']
class Gravity:
"""Gravity force between two objects."""
def __init__(self, m, M):
self.m = m
self.M = M
self.G = 6.67428E-11 # gravity constant
def force(self, r):
G, m, M = self.G, self.m, self.M
return G*m*M/r**2
def visualize(self, r_start, r_stop, n=100):
from scitools.std import plot, linspace
r = linspace(r_start, r_stop, n)
g = self.force(r)
title='m=%g, M=%g' % (self.m, self.M)
plot(r, g, title=title)
mass_moon = 7.35E+22
mass_earth = 5.97E+24
# make instance of class Gravity:
gravity = Gravity(mass_moon, mass_earth)
r = 3.85E+8 # earth-moon distance in meters
Fg = gravity.force(r) # call class method
c = a + b implies c = a.__add__(b)a+b, a-b, a*b, a/b, a**b, -a, if a:, len(a), str(a) (pretty print), repr(a) (recreate a with eval), etc.v = c(5) means v = c.__call__(5)
Consider measuring gravity \( g \) by dropping a ball from \( y=y_0 \) to \( y=0 \) in time \( T \): $$ g = 2y_0T^{-2} $$
What if \( y_0 \) and \( T \) are uncertain? Say \( y_0\in [0.99,1.01] \) m and \( T\in [0.43, 0.47] \) s. What is the uncertainty in \( g \)?
Rules for computing with intervals, \( p=[a,b] \) and \( q=[c,d] \):
class IntervalMath:
def __init__(self, lower, upper):
self.lo = float(lower)
self.up = float(upper)
def __add__(self, other):
a, b, c, d = self.lo, self.up, other.lo, other.up
return IntervalMath(a + c, b + d)
def __sub__(self, other):
a, b, c, d = self.lo, self.up, other.lo, other.up
return IntervalMath(a - d, b - c)
def __mul__(self, other):
a, b, c, d = self.lo, self.up, other.lo, other.up
return IntervalMath(min(a*c, a*d, b*c, b*d),
max(a*c, a*d, b*c, b*d))
def __div__(self, other):
a, b, c, d = self.lo, self.up, other.lo, other.up
if c*d <= 0: return None
return IntervalMath(min(a/c, a/d, b/c, b/d),
max(a/c, a/d, b/c, b/d))
def __str__(self):
return '[%g, %g]' % (self.lo, self.up)
I = IntervalMath # abbreviate
a = I(-3,-2)
b = I(4,5)
expr = 'a+b', 'a-b', 'a*b', 'a/b' # test expressions
for e in expr:
print e, '=', eval(e)
a+b = [1, 3]
a-b = [-8, -6]
a*b = [-15, -8]
a/b = [-0.75, -0.4]
This code
a = I(4,5)
q = 2
b = a*q
leads to
File "IntervalMath.py", line 15, in __mul__
a, b, c, d = self.lo, self.up, other.lo, other.up
AttributeError: 'float' object has no attribute 'lo'
Problem: IntervalMath times int is not defined.
Remedy: (cf. class Complex)
class IntervalArithmetics:
...
def __mul__(self, other):
if isinstance(other, (int, float)): # NEW
other = IntervalMath(other, other) # NEW
a, b, c, d = self.lo, self.up, other.lo, other.up
return IntervalMath(min(a*c, a*d, b*c, b*d),
max(a*c, a*d, b*c, b*d))
(with similar adjustments of other special methods)
Try to compute g = 2*y0*T**(-2):
multiplication of int (2) and
IntervalMath (y0),
and power operation T**(-2) are not defined
class IntervalArithmetics:
...
def __rmul__(self, other):
if isinstance(other, (int, float)):
other = IntervalMath(other, other)
return other*self
def __pow__(self, exponent):
if isinstance(exponent, int):
p = 1
if exponent > 0:
for i in range(exponent):
p = p*self
elif exponent < 0:
for i in range(-exponent):
p = p*self
p = 1/p
else: # exponent == 0
p = IntervalMath(1, 1)
return p
else:
raise TypeError('exponent must int')
"Rounding" to the midpoint value:
>>> a = IntervalMath(5,7)
>>> float(a)
6
is achieved by
class IntervalArithmetics:
...
def __float__(self):
return 0.5*(self.lo + self.up)
class IntervalArithmetics:
...
def __str__(self):
return '[%g, %g]' % (self.lo, self.up)
def __repr__(self):
return '%s(%g, %g)' % \
(self.__class__.__name__, self.lo, self.up)
>>> g = 9.81
>>> y_0 = I(0.99, 1.01)
>>> Tm = 0.45 # mean T
>>> T = I(Tm*0.95, Tm*1.05) # 10% uncertainty
>>> print T
[0.4275, 0.4725]
>>> g = 2*y_0*T**(-2)
>>> g
IntervalMath(8.86873, 11.053)
>>> # computing with mean values:
>>> T = float(T)
>>> y = 1
>>> g = 2*y_0*T**(-2)
>>> print '%.2f' % g
9.88
>>> R = I(6*0.9, 6*1.1) # 20 % error
>>> V = (4./3)*pi*R**3
>>> V
IntervalMath(659.584, 1204.26)
>>> print V
[659.584, 1204.26]
>>> print float(V)
931.922044761
>>> # compute with mean values:
>>> R = float(R)
>>> V = (4./3)*pi*R**3
>>> print V
904.778684234
20% uncertainty in \( R \) gives almost 60% uncertainty in \( V \)