INF5620 in a nutshell
The new official six-point course description
More specific contents: finite difference methods
More specific contents: finite element methods
More specific contents: nonlinear and advanced problems
Philosophy: simplify, understand, generalize
Required software
Assumed/ideal background
Start-up example for the course
Start-up example
What to learn in the start-up example; standard topics
What to learn in the start-up example; programming topics
What to learn in the start-up example; mathematical analysis
What to learn in the start-up example; generalizations
Finite difference methods
Topics in the first intro to the finite difference method
A basic model for exponential decay
The ODE model has a range of applications in many fields
The ODE problem has a continuous and discrete version
The steps in the finite difference method
Step 1: Discretizing the domain
Step 1: Discretizing the domain
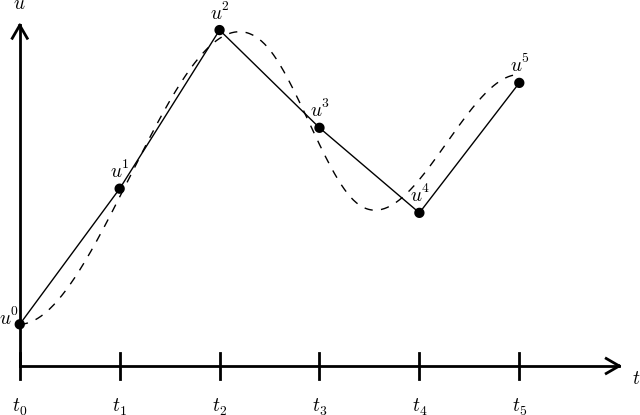
What about a mesh function between the mesh points?
Step 2: Fulfilling the equation at discrete time points
Step 3: Replacing derivatives by finite differences
Step 3: Replacing derivatives by finite differences
Step 4: Formulating a recursive algorithm
Let us apply the scheme by hand
A backward difference
The Backward Euler scheme
A centered difference
The Crank-Nicolson scheme; ideas
The Crank-Nicolson scheme; result
The unifying \( \theta \)-rule
Constant time step
Test the understanding!
Compact operator notation for finite differences
Specific notation for difference operators
The Backward Euler scheme with operator notation
The Forward Euler scheme with operator notation
The Crank-Nicolson scheme with operator notation
Implementation
Requirements of a program
Tools to learn
Why implement in Python?
Why implement in Python?
Algorithm
Translation to Python function
Integer division
Doc strings
Formatting of numbers
Running the program
Plotting the solution
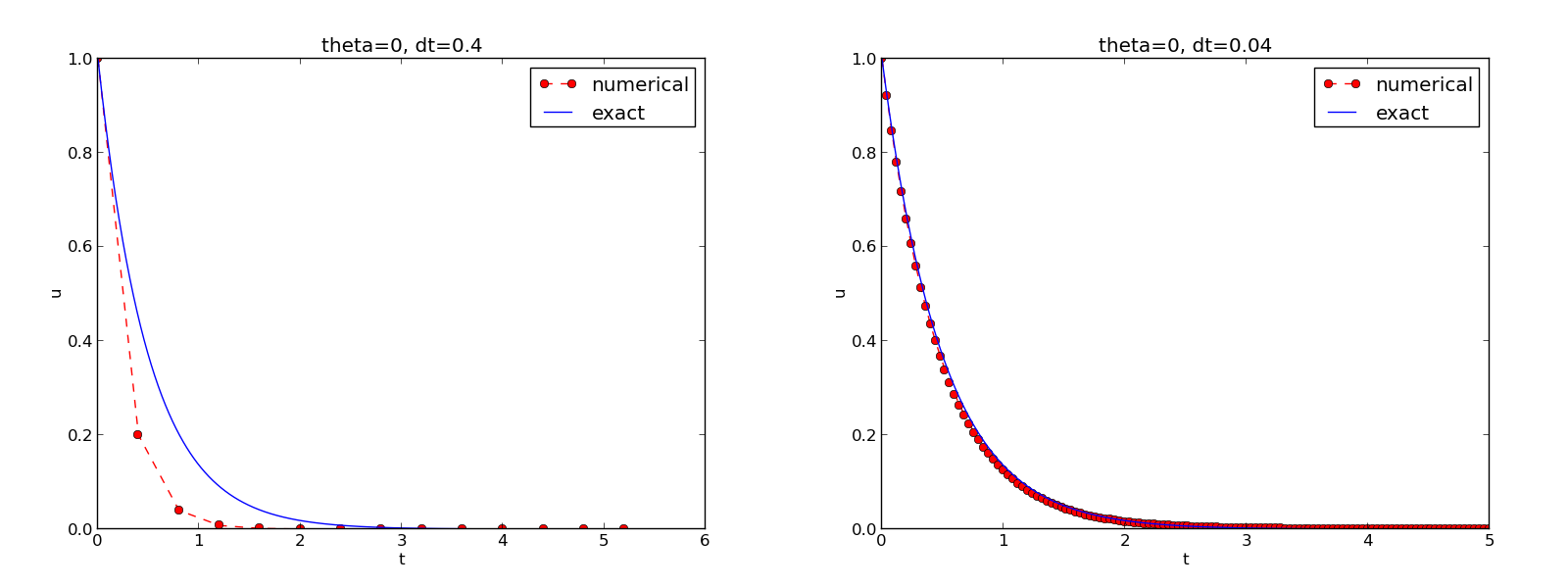
Comparing with the exact solution
Add legends, axes labels, title, and wrap in a function
Plotting with SciTools
Verifying the implementation
Simplest method: run a few algorithmic steps by hand
Comparison with an exact discrete solution
Making a test based on an exact discrete solution
Test the understanding!
Computing the numerical error as a mesh function
Computing the norm of the error
Norms of mesh functions
Implementation of the norm of the error
Comment on array vs scalar computation
Memory-saving implementation
Memory-saving solver function
Reading computed data from file
Usage of memory-saving code
You see a PDE and can't wait to program a method and visualize a solution! Somebody asks if the solution is right and you can give a convincing answer.
After having completed INF5620 you
numpy, scipy, matplotlib,
sympy, fenics, scitools, ...What if you don't have this ideal background?
$$ u'=-au,\quad u(0)=I,\ t\in (0,T],$$ where \( a>0 \) is a constant.
Everything we do is motivated by what we need as building blocks for solving PDEs!
sympy software
for symbolic computation
The world's simplest (?) ODE: $$ \begin{equation*} u'(t) = -au(t),\quad u(0)=I,\ t\in (0,T] \end{equation*} $$
We can learn a lot about numerical methods, computer implementation, program testing, and real applications of these tools by using this very simple ODE as example. The teaching principle is to keep the math as simple as possible while learning computer tools.
Numerical methods applied to the continuous problem turns it into a discrete problem $$ \begin{equation} u^{n+1} = \mbox{const} \cdot u^n, \quad n=0,1,\ldots N_t-1, \quad u^n=I \label{decay:problem:discrete} \end{equation} $$ (varies with discrete mesh points \( t_n \))
Solving a differential equation by a finite difference method consists of four steps:
The time domain \( [0,T] \) is represented by a mesh: a finite number of \( N_t+1 \) points $$0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T$$
\( u^n \) is a mesh function, defined at the mesh points \( t_n \), \( n=0,\ldots,N_t \) only.
Can extend the mesh function to yield values between mesh points by linear interpolation: $$ \begin{equation} u(t) \approx u^n + \frac{u^{n+1}-u^n}{t_{n+1}-t_n}(t - t_n) \label{_auto1} \end{equation} $$

Now it is time for the finite difference approximations of derivatives: $$ \begin{equation} u'(t_n) \approx \frac{u^{n+1}-u^{n}}{t_{n+1}-t_n} \label{decay:FEdiff} \end{equation} $$

Inserting the finite difference approximation in $$ u'(t_n) = -au(t_n)$$ gives $$ \begin{equation} \frac{u^{n+1}-u^{n}}{t_{n+1}-t_n} = -au^{n},\quad n=0,1,\ldots,N_t-1 \label{decay:step3} \end{equation} $$
(Known as discrete equation, or discrete problem, or finite difference method/scheme)
How can we actually compute the \( u^n \) values?
Solve wrt \( u^{n+1} \) to get the computational formula: $$ \begin{equation} u^{n+1} = u^n - a(t_{n+1} -t_n)u^n \label{decay:FE} \end{equation} $$
Assume constant time spacing: \( \Delta t = t_{n+1}-t_n=\mbox{const} \) $$ \begin{align*} u_0 &= I,\\ u_1 & = u^0 - a\Delta t u^0 = I(1-a\Delta t),\\ u_2 & = I(1-a\Delta t)^2,\\ u^3 &= I(1-a\Delta t)^3,\\ &\vdots\\ u^{N_t} &= I(1-a\Delta t)^{N_t} \end{align*} $$
Ooops - we can find the numerical solution by hand (in this simple example)! No need for a computer (yet)...
Here is another finite difference approximation to the derivative (backward difference): $$ \begin{equation} u'(t_n) \approx \frac{u^{n}-u^{n-1}}{t_{n}-t_{n-1}} \label{decay:BEdiff} \end{equation} $$
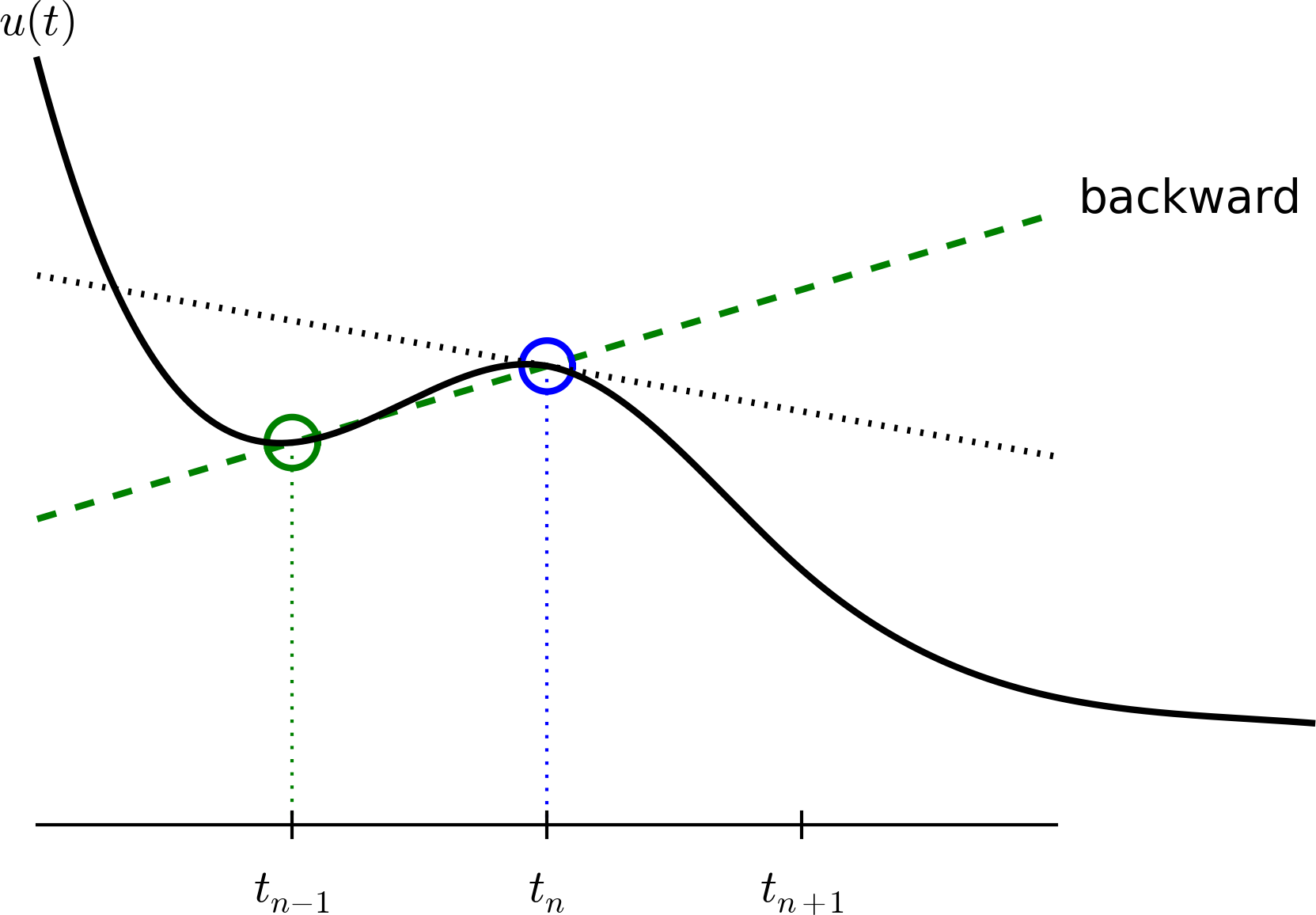
Inserting the finite difference approximation in \( u'(t_n)=-au(t_n) \) yields the Backward Euler (BE) scheme: $$ \begin{equation} \frac{u^{n}-u^{n-1}}{t_{n}-t_{n-1}} = -a u^n \label{decay:BE0} \end{equation} $$ Solve with respect to the unknown \( u^{n+1} \): $$ \begin{equation} u^{n+1} = \frac{1}{1+ a(t_{n+1}-t_n)} u^n \label{decay:BE} \end{equation} $$
Centered differences are better approximations than forward or backward differences.
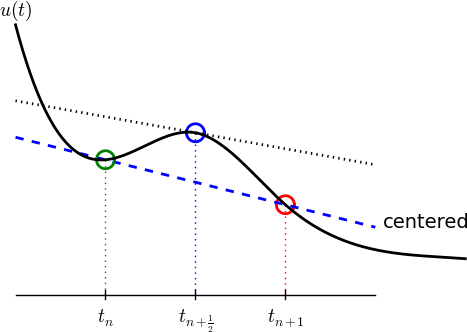
Idea 1: let the ODE hold at \( t_{n+\half} \) $$ u'(t_{n+\half}) = -au(t_{n+\half})$$
Idea 2: approximate \( u'(t_{n+\half}) \) by a centered difference $$ \begin{equation} u'(t_{n+\half}) \approx \frac{u^{n+1}-u^n}{t_{n+1}-t_n} \label{decay:CNdiff} \end{equation} $$
Problem: \( u(t_{n+\half}) \) is not defined, only \( u^n=u(t_n) \) and \( u^{n+1}=u(t_{n+1}) \)
Solution: $$ u(t_{n+\half}) \approx \half(u^n + u^{n+1}) $$
Result: $$ \begin{equation} \frac{u^{n+1}-u^n}{t_{n+1}-t_n} = -a\half (u^n + u^{n+1}) \label{decay:CN1} \end{equation} $$
Solve wrt to \( u^{n+1} \): $$ \begin{equation} u^{n+1} = \frac{1-\half a(t_{n+1}-t_n)}{1 + \half a(t_{n+1}-t_n)}u^n \label{decay:CN} \end{equation} $$ This is a Crank-Nicolson (CN) scheme or a midpoint or centered scheme.
The Forward Euler, Backward Euler, and Crank-Nicolson schemes can be formulated as one scheme with a varying parameter \( \theta \): $$ \begin{equation} \frac{u^{n+1}-u^{n}}{t_{n+1}-t_n} = -a (\theta u^{n+1} + (1-\theta) u^{n}) \label{decay:th0} \end{equation} $$
Very common assumption (not important, but exclusively used for simplicity hereafter): constant time step \( t_{n+1}-t_n\equiv\Delta t \)
$$ \begin{align} u^{n+1} &= (1 - a\Delta t )u^n \quad (\hbox{FE}) \label{decay:FE:u}\\ u^{n+1} &= \frac{1}{1+ a\Delta t} u^n \quad (\hbox{BE}) \label{decay:BE:u}\\ u^{n+1} &= \frac{1-\half a\Delta t}{1 + \half a\Delta t} u^n \quad (\hbox{CN}) \label{decay:CN:u}\\ u^{n+1} &= \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n \quad (\theta-\hbox{rule}) \label{decay:th:u} \end{align} $$
Derive Forward Euler, Backward Euler, and Crank-Nicolson schemes for Newton's law of cooling: $$ T' = -k(T-T_s),\quad T(0)=T_0,\ t\in (0,t_{\mbox{end}}]$$
Physical quantities:
Forward difference: $$ \begin{equation} [D_t^+u]^n = \frac{u^{n+1} - u^{n}}{\Delta t} \approx \frac{d}{dt} u(t_n) \label{fd:D:f} \end{equation} $$ Centered difference (around \( t_n \)): $$ \begin{equation} [D_tu]^n = \frac{u^{n+\half} - u^{n-\half}}{\Delta t} \approx \frac{d}{dt} u(t_n), \label{fd:D:c} \end{equation} $$
Backward difference: $$ \begin{equation} [D_t^-u]^n = \frac{u^{n} - u^{n-1}}{\Delta t} \approx \frac{d}{dt} u(t_n) \label{fd:D:b} \end{equation} $$
Common to put the whole equation inside square brackets: $$ \begin{equation} [D_t^- u = -au]^n \label{_auto3} \end{equation} $$
Introduce an averaging operator: $$ \begin{equation} [\overline{u}^{t}]^n = \half (u^{n-\half} + u^{n+\half} ) \approx u(t_n) \label{fd:mean:a} \end{equation} $$
The Crank-Nicolson scheme can then be written as $$ \begin{equation} [D_t u = -a\overline{u}^t]^{n+\half} \label{fd:compact:ex:CN} \end{equation} $$
Test: use the definitions and write out the above formula to see that it really is the Crank-Nicolson scheme!
Model: $$ u'(t) = -au(t),\quad t\in (0,T], \quad u(0)=I $$
Numerical method: $$ u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n $$ for \( \theta\in [0,1] \). Note
All programs are in the directory src/alg.
u.
from numpy import *
def solver(I, a, T, dt, theta):
"""Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
Nt = int(T/dt) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
return u, t
Note about the for loop: range(0, Nt, s) generates all integers
from 0 to Nt in steps of s (default 1), but not including Nt (!).
Sample call:
u, t = solver(I=1, a=2, T=8, dt=0.8, theta=1)
Python applies integer division: 1/2 is 0, while 1./2 or 1.0/2 or
1/2. or 1/2.0 or 1.0/2.0 all give 0.5.
A safer solver function (dt = float(dt) - guarantee float):
from numpy import *
def solver(I, a, T, dt, theta):
"""Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
return u, t
def solver(I, a, T, dt, theta):
"""
Solve
u'(t) = -a*u(t),
with initial condition u(0)=I, for t in the time interval
(0,T]. The time interval is divided into time steps of
length dt.
theta=1 corresponds to the Backward Euler scheme, theta=0
to the Forward Euler scheme, and theta=0.5 to the Crank-
Nicolson method.
"""
...
Can control formatting of reals and integers through the printf format:
print 't=%6.3f u=%g' % (t[i], u[i])
Or the alternative format string syntax:
print 't={t:6.3f} u={u:g}'.format(t=t[i], u=u[i])
How to run the program decay_v1.py.
Terminal> python decay_v1.py
Can also run it as "normal" Unix programs: ./decay_v1.py if the
first line is
`#!/usr/bin/env python`
Then
Terminal> chmod a+rx decay_v1.py
Terminal> ./decay_v1.py
Basic syntax:
from matplotlib.pyplot import *
plot(t, u)
show()
Can (and should!) add labels on axes, title, legends.
Python function for the exact solution \( \uex(t)=Ie^{-at} \):
def u_exact(t, I, a):
return I*exp(-a*t)
Quick plotting:
u_e = u_exact(t, I, a)
plot(t, u, t, u_e)
Problem: \( \uex(t) \) applies the same mesh as \( u^n \) and looks as a piecewise linear function.
Remedy: Introduce a very fine mesh for \( \uex \).
t_e = linspace(0, T, 1001) # fine mesh
u_e = u_exact(t_e, I, a)
plot(t_e, u_e, 'b-', # blue line for u_e
t, u, 'r--o') # red dashes w/circles
from matplotlib.pyplot import *
def plot_numerical_and_exact(theta, I, a, T, dt):
"""Compare the numerical and exact solution in a plot."""
u, t = solver(I=I, a=a, T=T, dt=dt, theta=theta)
t_e = linspace(0, T, 1001) # fine mesh for u_e
u_e = u_exact(t_e, I, a)
plot(t, u, 'r--o', # red dashes w/circles
t_e, u_e, 'b-') # blue line for exact sol.
legend(['numerical', 'exact'])
xlabel('t')
ylabel('u')
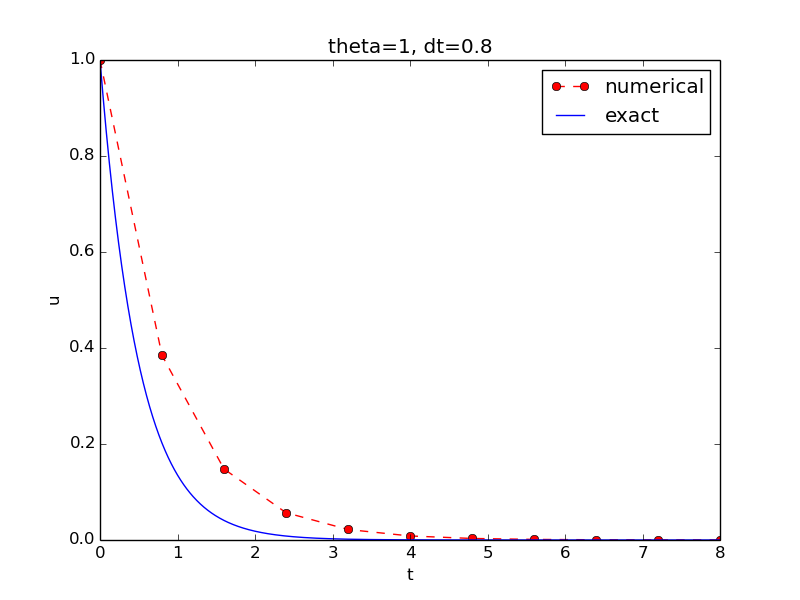
title('theta=%g, dt=%g' % (theta, dt))
savefig('plot_%s_%g.png' % (theta, dt))
Complete code in decay_v2.py
SciTools provides a unified plotting interface (Easyviz) to many different plotting packages: Matplotlib, Gnuplot, Grace, VTK, OpenDX, ...
Can use Matplotlib (MATLAB-like) syntax,
or a more compact plot function syntax:
from scitools.std import *
plot(t, u, 'r--o', # red dashes w/circles
t_e, u_e, 'b-', # blue line for exact sol.
legend=['numerical', 'exact'],
xlabel='t',
ylabel='u',
title='theta=%g, dt=%g' % (theta, dt),
savefig='%s_%g.png' % (theta2name[theta], dt),
show=True)
Change backend (plotting engine, Matplotlib by default):
Terminal> python decay_plot_st.py --SCITOOLS_easyviz_backend gnuplot
Terminal> python decay_plot_st.py --SCITOOLS_easyviz_backend grace
Use a calculator (\( I=0.1 \), \( \theta=0.8 \), \( \Delta t =0.8 \)): $$ A\equiv \frac{1 - (1-\theta) a\Delta t}{1 + \theta a \Delta t} = 0.298245614035$$ $$ \begin{align*} u^1 &= AI=0.0298245614035,\\ u^2 &= Au^1= 0.00889504462912,\\ u^3 &=Au^2= 0.00265290804728 \end{align*} $$
See the function test_solver_three_steps in decay_v3.py.
Compare computed numerical solution with a closed-form exact discrete solution (if possible).
Define $$ A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a \Delta t}$$ Repeated use of the \( \theta \)-rule: $$ \begin{align*} u^0 &= I,\\ u^1 &= Au^0 = AI\\ u^n &= A^nu^{n-1} = A^nI \end{align*} $$
The exact discrete solution is $$ \begin{equation} u^n = IA^n \label{decay:un:exact} \end{equation} $$
Understand what \( n \) in \( u^n \) and in \( A^n \) means!
Test if $$ \max_n |u^n - \uex(t_n)| < \epsilon\sim 10^{-15}$$
Implementation in decay_verf2.py.
Make a program for solving Newton's law of cooling $$ T' = -k(T-T_s),\quad T(0)=T_0,\ t\in (0,t_{\mbox{end}}]$$ with the Forward Euler, Backward Euler, and Crank-Nicolson schemes (or a \( \theta \) scheme). Verify the implementation.
Task: compute the numerical error \( e^n = \uex(t_n) - u^n \)
Exact solution: \( \uex(t)=Ie^{-at} \), implemented as
def u_exact(t, I, a):
return I*exp(-a*t)
Compute \( e^n \) by
u, t = solver(I, a, T, dt, theta) # Numerical solution
u_e = u_exact(t, I, a)
e = u_e - u
u_exact(t, I, a) works with t as arrayexp from numpy (not math)e = u_e - u: array subtraction
Common simplification yields the \( L^2 \) norm of a mesh function: $$ ||f^n||_{\ell^2} = \left(\Delta t\sum_{n=0}^{N_t} (f^n)^2\right)^{1/2}$$
Python w/array arithmetics:
e = u_exact(t) - u
E = sqrt(dt*sum(e**2))
Scalar computing of E = sqrt(dt*sum(e**2)):
m = len(u) # length of u array (alt: u.size)
u_e = zeros(m)
t = 0
for i in range(m):
u_e[i] = u_exact(t, a, I)
t = t + dt
e = zeros(m)
for i in range(m):
e[i] = u_e[i] - u[i]
s = 0 # summation variable
for i in range(m):
s = s + e[i]**2
error = sqrt(dt*s)
Obviously, scalar computing
Compute on entire arrays (when possible)!
u, i.e., \( u^n \) for \( n=0,1,\ldots,N_t \)u, \( u^n \) in u_1 (float)u in a file, read file later for plotting
def solver_memsave(I, a, T, dt, theta, filename='sol.dat'):
"""
Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt.
Minimum use of memory. The solution is stored in a file
(with name filename) for later plotting.
"""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of intervals
outfile = open(filename, 'w')
# u: time level n+1, u_1: time level n
t = 0
u_1 = I
outfile.write('%.16E %.16E\n' % (t, u_1))
for n in range(1, Nt+1):
u = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u_1
u_1 = u
t += dt
outfile.write('%.16E %.16E\n' % (t, u))
outfile.close()
return u, t
def read_file(filename='sol.dat'):
infile = open(filename, 'r')
u = []; t = []
for line in infile:
words = line.split()
if len(words) != 2:
print 'Found more than two numbers on a line!', words
sys.exit(1) # abort
t.append(float(words[0]))
u.append(float(words[1]))
return np.array(t), np.array(u)
Simpler code with numpy functionality for reading/writing tabular data:
def read_file_numpy(filename='sol.dat'):
data = np.loadtxt(filename)
t = data[:,0]
u = data[:,1]
return t, u
Similar function np.savetxt, but then we need all \( u^n \) and \( t^n \) values
in a two-dimensional array (which we try to prevent now!).
def explore(I, a, T, dt, theta=0.5, makeplot=True):
filename = 'u.dat'
u, t = solver_memsave(I, a, T, dt, theta, filename)
t, u = read_file(filename)
u_e = u_exact(t, I, a)
e = u_e - u
E = np.sqrt(dt*np.sum(e**2))
if makeplot:
plt.figure()
...
Complete program: decay_memsave.py.