Performing scientific experiments

Goal

This section explores the behavior of a numerical method for a differential equation through computer experiments. In particular, it is shown how scientific experiments can be set up and reported. We address the ODE problem

(1)\[ u'(t) = -au(t),\quad u(0)=I,\quad t\in (0,T],\]\[numerically discretized by the :math:`\theta`-rule:\]\[ .. math::\]\[ u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n, \quad u^0=I{\thinspace .}\]\[ Our aim is to plot :math:`u^0,u^1,\ldots,u^N` together with the exact solution :math:`{u_{\small\mbox{e}}} = Ie^{-at}` for various choices of the parameters in this numerical problem: :math:`I`, :math:`a`, :math:`\Delta t`, and :math:`\theta`. We are especially interested in how the discrete solution compares with the exact solution when the :math:`\Delta t` parameter is varied and :math:`\theta` takes on the three values corresponding to the Forward Euler, Backward Euler, and Crank-Nicolson schemes (:math:`\theta=0,1,0.5`, respectively).\]

Software

A verified implementation for computing the numerical solution \(u^n\) and plotting it together with the exact solution \({u_{\small\mbox{e}}}\) is found in the file decay_mod.py. This program admits command-line arguments to specify a series of \(\Delta t\) values and will run a loop over these values and \(\theta=0,0.5,1\). We make a slight edit of how the plots are designed: the numerical solution is specified with line type 'r--o' (dashed red lines with dots at the mesh points), and the show() command is removed to avoid a lot of plot windows popping up on the computer screen (but hardcopies of the plot are still stored in files via savefig). The slightly modified program has the name experiments/decay_mod.py. All files associated with the scientific investigation are collected in a subdirectory experiments.

Running the experiments is easy since the decay_mod.py program already has the loops over \(\theta\) and \(\Delta t\) implemented. An experiment with \(I=1\), \(a=2\), \(T=5\), and \(dt=0.5, 0.25, 0.1, 0.05\) is run by

Terminal> python decay_mod.py --I 1 --a 2 --makeplot \
          --T 5 --dt 0.5 0.25 0.1 0.05

Combining plot files (2)

The decay_mod.py program generates a lot of image files, e.g., FE_*.png, BE_*.png, and CN_*.png. We want to combine all the FE_*.png files in a table fashion in one file, with two images in each row, starting with the largest \(\Delta t\) in the upper left corner and decreasing the value as we go to the right and down. This can be done using the montage program. The often occurring white areas around the plots can be cropped away by the convert -trim command. The remaining white can be made transparent for HTML pages with a non-white background by the command convert -transparent white.

Also plot files in the PDF format with names FE_*.pdf, BE_*.pdf, and CN_*.pdf are generated and these should be combined using other tools: pdftk to combine individual plots into one file with one plot per page, and pdfnup to combine the pages into a table with multiple plots per page. The resulting image often has some extra surrounding white space that can be removed by the pdfcrop program. The code snippets below contain all details about the usage of montage, convert, pdftk, pdfnup, and pdfcrop.

Running manual commands is boring, and errors may easily sneak in. Both for automating manual work and documenting the operating system commands we actually issued in the experiment, we should write a script (little program). An alternative is to write the commands into an IPython notebook and use the notebook as the script. A plain script as a standard Python program in a separate text file will be used here.

Reproducible science

A script that automates running our computer experiments will ensure that the experiments can easily be rerun by ourselves or others in the future, either to check the results or redo the experiments with other input data. Also, whatever we did to produce the results is documented in every detail in the script. Automating scripts are therefore essential to making our research reproducible, which is a fundamental principle in science.

The script takes a list of \(\Delta t\) values on the command line as input and makes three combined images, one for each \(\theta\) value, displaying the quality of the numerical solution as \(\Delta t\) varies. For example,

Terminal> python decay_exper0.py 0.5 0.25 0.1 0.05

results in images FE.png, CN.png, BE.png, FE.pdf, CN.pdf, and BE.pdf, each with four plots corresponding to the four \(\Delta t\) values. Each plot compares the numerical solution with the exact one. The latter image is shown in Figure Illustration of the Backward Euler method for four time step values.

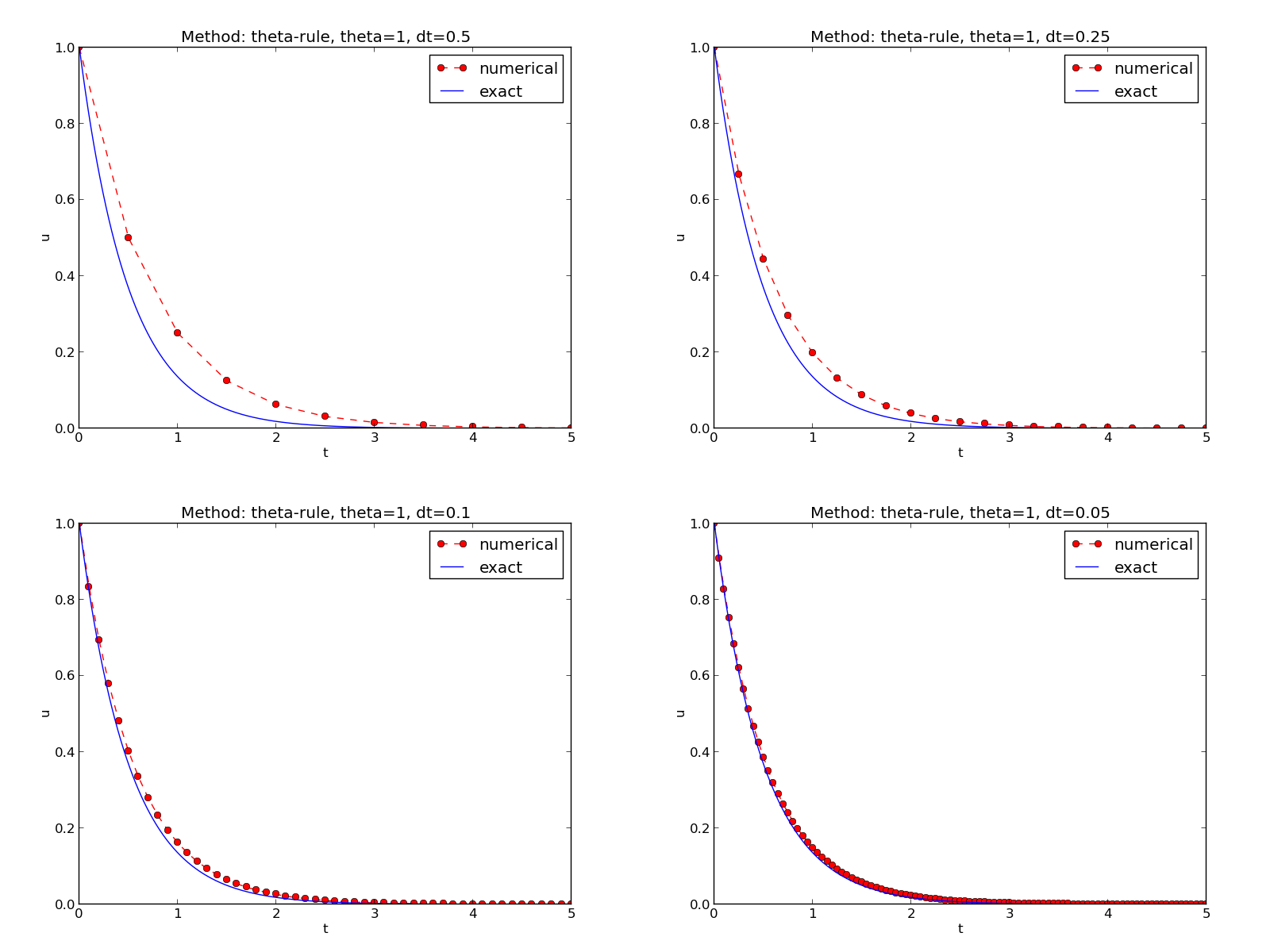
Illustration of the Backward Euler method for four time step values

Ideally, the script should be scalable in the sense that it works for any number of \(\Delta t\) values, which is the case for this particular implementation:

import os, sys

def run_experiments(I=1, a=2, T=5):
    # The command line must contain dt values
    if len(sys.argv) > 1:
        dt_values = [float(arg) for arg in sys.argv[1:]]
    else:
        print 'Usage: %s dt1 dt2 dt3 ...' %  sys.argv[0]
        sys.exit(1)  # abort

    # Run module file as a stand-alone application
    cmd = 'python decay_mod.py --I %g --a %g --makeplot --T %g' % \
          (I, a, T)
    dt_values_str = ' '.join([str(v) for v in dt_values])
    cmd += ' --dt %s' % dt_values_str
    print cmd
    failure = os.system(cmd)
    if failure:
        print 'Command failed:', cmd; sys.exit(1)

    # Combine images into rows with 2 plots in each row
    image_commands = []
    for method in 'BE', 'CN', 'FE':
        pdf_files = ' '.join(['%s_%g.pdf' % (method, dt)
                              for dt in dt_values])
        png_files = ' '.join(['%s_%g.png' % (method, dt)
                              for dt in dt_values])
        image_commands.append(
            'montage -background white -geometry 100%' +
            ' -tile 2x %s %s.png' % (png_files, method))
        image_commands.append(
            'convert -trim %s.png %s.png' % (method, method))
        image_commands.append(
            'convert %s.png -transparent white %s.png' %
            (method, method))
        image_commands.append(
            'pdftk %s output tmp.pdf' % pdf_files)
        num_rows = int(round(len(dt_values)/2.0))
        image_commands.append(
            'pdfnup --nup 2x%d tmp.pdf' % num_rows)
        image_commands.append(
            'pdfcrop tmp-nup.pdf %s.pdf' % method)

    for cmd in image_commands:
        print cmd
        failure = os.system(cmd)
        if failure:
            print 'Command failed:', cmd; sys.exit(1)

    # Remove the files generated above and by decay_mod.py
    from glob import glob
    filenames = glob('*_*.png') + glob('*_*.pdf') + \
                glob('*_*.eps') + glob('tmp*.pdf')
    for filename in filenames:
        os.remove(filename)

if __name__ == '__main__':
    run_experiments()

This file is available as experiments/decay_exper0.py.

We may comment upon many useful constructs in this script:

• [float(arg) for arg in sys.argv[1:]] builds a list of real numbers from all the command-line arguments.
• failure = os.system(cmd) runs an operating system command, e.g., another program. The execution is successful only if failure is zero.
• Unsuccessful execution usually makes it meaningless to continue the program, and therefore we abort the program with sys.exit(1). Any argument different from 0 signifies to the computer’s operating system that our program stopped with a failure.
• ['%s_%s.png' % (method, dt) for dt in dt_values] builds a list of filenames from a list of numbers (dt_values).
• All montage, convert, pdftk, pdfnup, and pdfcrop commands for creating composite figures are stored in a list and later executed in a loop.
• glob('*_*.png') returns a list of the names of all files in the current directory where the filename matches the Unix wildcard notation *_*.png (meaning any text, underscore, any text, and then .png).
• os.remove(filename) removes the file with name filename.

Interpreting output from other programs

Programs that run other programs, like decay_exper0.py does, will often need to interpret output from those programs. Let us demonstrate how this is done in Python by extracting the relations between \(\theta\), \(\Delta t\), and the error \(E\) as written to the terminal window by the decay_mod.py program, when being executed by decay_exper0.py. We will

• read the output from the decay_mod.py program
• interpret this output and store the \(E\) values in arrays for each \(\theta\) value
• plot \(E\) versus \(\Delta t\), for each \(\theta\), in a log-log plot

The simple os.system(cmd) call does not allow us to read the output from running cmd. Instead we need to invoke a bit more involved procedure:

from subprocess import Popen, PIPE, STDOUT
p = Popen(cmd, shell=True, stdout=PIPE, stderr=STDOUT)
output, dummy = p.communicate()
failure = p.returncode
if failure:
    print 'Command failed:', cmd; sys.exit(1)

The command stored in cmd is run and all text that is written to the standard output and the standard error is available in the string output. Or in other words, the text in output is what appeared in the terminal window while running cmd.

Our next task is to run through the output string, line by line, and if the current line prints \(\theta\), \(\Delta t\), and \(E\), we split the line into these three pieces and store the data. The chosen storage structure is a dictionary errors with keys dt to hold the \(\Delta t\) values in a list, and three \(\theta\) keys to hold the corresponding \(E\) values in a list. The relevant code lines are

errors = {'dt': dt_values, 1: [], 0: [], 0.5: []}
for line in output.splitlines():
    words = line.split()
    if words[0] in ('0.0', '0.5', '1.0'):  # line with E?
        # typical line: 0.0   1.25:    7.463E+00
        theta = float(words[0])
        E = float(words[2])
        errors[theta].append(E)

Note that we do not bother to store the \(\Delta t\) values as we read them from output, because we already have these values in the dt_values list.

We are now ready to plot \(E\) versus \(\Delta t\) for \(\theta=0,0.5,1\):

import matplotlib.pyplot as plt
plt.loglog(errors['dt'], errors[0], 'ro-')
plt.hold('on')
plt.loglog(errors['dt'], errors[0.5], 'b+-')
plt.loglog(errors['dt'], errors[1], 'gx-')
plt.legend(['FE', 'CN', 'BE'], loc='upper left')
plt.xlabel('log(time step)')
plt.ylabel('log(error)')
plt.title('Error vs time step')
plt.savefig('error.png')
plt.savefig('error.pdf')

Plots occasionally need some manual adjustments. Here, the axis of the log-log plot look nicer if we adapt them strictly to the data, see Figure Default plot (left) and manually adjusted axes (right). To this end, we need to compute \(\min E\) and \(\max E\), and later specify the extent of the axes:

# Find min/max for the axis
E_min = 1E+20; E_max = -E_min
for theta in 0, 0.5, 1:
    E_min = min(E_min, min(errors[theta]))
    E_max = max(E_max, max(errors[theta]))

plt.loglog(errors['dt'], errors[0], 'ro-')
...
plt.axis([min(dt_values), max(dt_values), E_min, E_max])
...

Default plot (left) and manually adjusted axes (right)

The complete program, incorporating the code snippets above, is found in experiments/decay_exper1.py. This example can hopefully act as template for numerous other occasions where one needs to run experiments, extract data from the output of programs, make plots, and combine several plots in a figure file. The decay_exper1.py program is organized as a module, and other files can then easily extend the functionality, as illustrated in the next section.

Making a report

The results of running computer experiments are best documented in a little report containing the problem to be solved, key code segments, and the plots from a series of experiments. At least the part of the report containing the plots should be automatically generated by the script that performs the set of experiments, because in that script we know exactly which input data that were used to generate a specific plot, thereby ensuring that each figure is connected to the right data. Take a look at an example at http://tinyurl.com/k3sdbuv/writing_reports//sphinx-cloud/ to see what we have in mind.

Plain HTML

Scientific reports can be written in a variety of formats. Here we begin with the HTML format which allows efficient viewing of all the experiments in any web browser. The program decay_exper1_html.py calls decay_exper1.py to perform the experiments and then runs statements for creating an HTML file with a summary, a section on the mathematical problem, a section on the numerical method, a section on the solver function implementing the method, and a section with subsections containing figures that show the results of experiments where \(\Delta t\) is varied for \(\theta=0,0.5,1\). The mentioned Python file contains all the details for writing this HTML report. You can view the report on http://tinyurl.com/k3sdbuv/writing_reports//_static/report_html.html.

HTML with MathJax

Scientific reports usually need mathematical formulas and hence mathematical typesetting. In plain HTML, as used in the decay_exper1_html.py file, we have to use just the keyboard characters to write mathematics. However, there is an extension to HTML, called MathJax, which allows formulas and equations to be typeset with LaTeX syntax and nicely rendered in web browsers, see Figure Report in HTML format with MathJax. A relatively small subset of LaTeX environments is supported, but the syntax for formulas is quite rich. Inline formulas are look like \( u'=-au \) while equations are surrounded by $$ signs. Inside such signs, one can use \[ u'=-au \] for unnumbered equations, or \begin{equation} and \end{equation} surrounding u'=-au for numbered equations, or \begin{equation} and \end{equation} for multiple aligned equations. You need to be familiar with mathematical typesetting in LaTeX.

The file decay_exper1_mathjax.py contains all the details for turning the previous plain HTML report into web pages with nicely typeset mathematics. The corresponding HTML code be studied to see all details of the mathematical typesetting.

Report in HTML format with MathJax

LaTeX

The de facto language for mathematical typesetting and scientific report writing is LaTeX. A number of very sophisticated packages have been added to the language over a period of three decades, allowing very fine-tuned layout and typesetting. For output in the PDF format, see Figure Report in PDF format generated from LaTeX source for an example, LaTeX is the definite choice when it comes to quality. The LaTeX language used to write the reports has typically a lot of commands involving backslashes and braces. For output on the web, using HTML (and not the PDF directly in the browser window), LaTeX struggles with delivering high quality typesetting. Other tools, especially Sphinx, give better results and can also produce nice-looking PDFs. The file decay_exper1_latex.py shows how to generate the LaTeX source from a program.

Report in PDF format generated from LaTeX source

Sphinx

Sphinx is a typesetting language with similarities to HTML and LaTeX, but with much less tagging. It has recently become very popular for software documentation and mathematical reports. Sphinx can utilize LaTeX for mathematical formulas and equations (via MathJax or PNG images). Unfortunately, the subset of LaTeX mathematics supported is less than in full MathJax (in particular, numbering of multiple equations in an align type environment is not supported). The Sphinx syntax is an extension of the reStructuredText language. An attractive feature of Sphinx is its rich support for fancy layout of web pages. In particular, Sphinx can easily be combined with various layout themes that give a certain look and feel to the web site and that offers table of contents, navigation, and search facilities, see Figure Report in HTML format generated from Sphinx source.

Report in HTML format generated from Sphinx source

Markdown

A recently popular format for easy writing of web pages is Markdown. Text is written very much like one would do in email, using spacing and special characters to naturally format the code instead of heavily tagging the text as in LaTeX and HTML. With the tool Pandoc one can go from Markdown to a variety of formats. HTML is a common output format, but LaTeX, epub, XML, OpenOffice, MediaWiki, and MS Word are some other possibilities.

Wiki formats

A range of wiki formats are popular for creating notes on the web, especially documents which allow groups of people to edit and add content. Apart from MediaWiki (the wiki format used for Wikipedia), wiki formats have no support for mathematical typesetting and also limited tools for displaying computer code in nice ways. Wiki formats are therefore less suitable for scientific reports compared to the other formats mentioned here.

Doconce

Since it is difficult to choose the right tool or format for writing a scientific report, it is advantageous to write the content in a format that easily translates to LaTeX, HTML, Sphinx, Markdown, and various wikis. Doconce is such a tool. It is similar to Pandoc, but offers some special convenient features for writing about mathematics and programming. The tagging is modest, somewhere between LaTeX and Markdown. The program decay_exper_do.py demonstrates how to generate (and write) Doconce code for a report.

Worked example

The HTML, LaTeX (PDF), Sphinx, and Doconce formats for the scientific report whose content is outlined above, are exemplified with source codes and results at the web pages associated with this teaching material: http://tinyurl.com/k3sdbuv/writing_reports/.

Publishing a complete project

A report documenting scientific investigations should be accompanied by all the software and data used for the investigations so that others have a possibility to redo the work and assess the qualify of the results. This possibility is important for reproducible research and hence reaching reliable scientific conclusions.

One way of documenting a complete project is to make a directory tree with all relevant files. Preferably, the tree is published at some project hosting site like Bitbucket, GitHub, or Googlecode so that others can download it as a tarfile, zipfile, or clone the files directly using a version control system like Mercurial or Git. For the investigations outlined in the section Making a report, we can create a directory tree with files

setup.py
./src:
   decay_mod.py
./doc:
   ./src:
      decay_exper1_mathjax.py
      make_report.sh
      run.sh
   ./pub:
      report.html

The src directory holds source code (modules) to be reused in other projects, the setup.py builds and installs such software, the doc directory contains the documentation, with src for the source of the documentation and pub for ready-made, published documentation. The run.sh file is a simple Bash script listing the python command we used to run decay_exper1_mathjax.py to generate the experiments and the report.html file.