Study Guide: Finite difference methods for vibration problems

A simple vibration problem

 
$$ \begin{equation} u''t + \omega^2u = 0,\quad u(0)=I,\ u'(0)=0,\ t\in (0,T] \tp \tag{1} \end{equation} $$

Exact solution:

 
$$ \begin{equation} u(t) = I\cos (\omega t) \tp \tag{2} \end{equation} $$

 
\( u(t) \) oscillates with constant amplitude \( I \) and (angular) frequency \( \omega \). Period: \( P=2\pi/\omega \).

A centered finite difference scheme; step 1 and 2

• Strategy: follow the four steps of the finite difference method.
• Step 1: Introduce a time mesh, here uniform on \( [0,T] \): \( t_n=n\Delta t \)
• Step 2: Let the ODE be satisfied at each mesh point:

 
$$ \begin{equation} u''(t_n) + \omega^2u(t_n) = 0,\quad n=1,\ldots,N_t \tp \tag{3} \end{equation} $$

A centered finite difference scheme; step 3

Step 3: Approximate derivative(s) by finite difference approximation(s). Very common (standard!) formula for \( u'' \):

 
$$ \begin{equation} u''(t_n) \approx \frac{u^{n+1}-2u^n + u^{n-1}}{\Delta t^2} \tp \tag{4} \end{equation} $$

Use this discrete initial condition together with the ODE at \( t=0 \) to eliminate \( u^{-1} \) (insert (4) in (3)):

 
$$ \begin{equation} \frac{u^{n+1}-2u^n + u^{n-1}}{\Delta t^2} = -\omega^2 u^n \tp \tag{5} \end{equation} $$

A centered finite difference scheme; step 4

Step 4: Formulate the computational algorithm. Assume \( u^{n-1} \) and \( u^n \) are known, solve for unknown \( u^{n+1} \):

 
$$ \begin{equation} u^{n+1} = 2u^n - u^{n-1} - \Delta t^2\omega^2 u^n \tp \tag{6} \end{equation} $$

Nick names for this scheme: Stormer's method or Verlet integration.

Computing the first step

• The formula breaks down for \( u^1 \) because \( u^{-1} \) is unknown and outside the mesh!
• And: we have not used the initial condition \( u'(0)=0 \).

Discretize \( u'(0)=0 \) by a centered difference

 
$$ \begin{equation} \frac{u^1-u^{-1}}{2\Delta t} = 0\quad\Rightarrow\quad u^{-1} = u^1 \tp \end{equation} $$

Inserted in (6) for \( n=0 \) gives

 
$$ \begin{equation} u^1 = u^0 - \half \Delta t^2 \omega^2 u^0 \tp \tag{7} \end{equation} $$

The computational algorithm

1. \( u^0=I \)
2. compute \( u^1 \) from (7)
3. for \( n=1,2,\ldots,N_t-1 \):

1. compute \( u^{n+1} \) from (6)

More precisly expressed in Python:

t = linspace(0, T, Nt+1)  # mesh points in time
dt = t[1] - t[0]          # constant time step.
u = zeros(Nt+1)           # solution

u[0] = I
u[1] = u[0] - 0.5*dt**2*w**2*u[0]
for n in range(1, Nt):
    u[n+1] = 2*u[n] - u[n-1] - dt**2*w**2*u[n]

Note: w is consistently used for \( \omega \) in my code.

Operator notation; ODE

With \( [D_tD_t u]^n \) as the finite difference approximation to \( u''(t_n) \) we can write

 
$$ \begin{equation} [D_tD_t u + \omega^2 u = 0]^n \tp \tag{8} \end{equation} $$

\( [D_tD_t u]^n \) means applying a central difference with step \( \Delta t/2 \) twice:

 
$$ [D_t(D_t u)]^n = \frac{[D_t u]^{n+\half} - [D_t u]^{n-\half}}{\Delta t}$$

 
which is written out as

 
$$ \frac{1}{\Delta t}\left(\frac{u^{n+1}-u^n}{\Delta t} - \frac{u^{n}-u^{n-1}}{\Delta t}\right) = \frac{u^{n+1}-2u^n + u^{n-1}}{\Delta t^2} \tp $$

Operator notation; initial condition

 
$$ \begin{equation} [u = I]^0,\quad [D_{2t} u = 0]^0, \end{equation} $$

 
where \( [D_{2t} u]^n \) is defined as

 
$$ \begin{equation} [D_{2t} u]^n = \frac{u^{n+1} - u^{n-1}}{2\Delta t} \tp \end{equation} $$

Computing \( u' \)

\( u \) is often displacement/position, \( u' \) is velocity and can be computed by

 
$$ \begin{equation} u'(t_n) \approx \frac{u^{n+1}-u^{n-1}}{2\Delta t} = [D_{2t}u]^n \tp \end{equation} $$

Implementation

Core algorithm

from numpy import *
from matplotlib.pyplot import *
from vib_empirical_analysis import minmax, periods, amplitudes

def solver(I, w, dt, T):
    """
    Solve u'' + w**2*u = 0 for t in (0,T], u(0)=I and u'(0)=0,
    by a central finite difference method with time step dt.
    """
    dt = float(dt)
    Nt = int(round(T/dt))
    u = zeros(Nt+1)
    t = linspace(0, Nt*dt, Nt+1)

    u[0] = I
    u[1] = u[0] - 0.5*dt**2*w**2*u[0]
    for n in range(1, Nt):
        u[n+1] = 2*u[n] - u[n-1] - dt**2*w**2*u[n]
    return u, t

Plotting

def exact_solution(t, I, w):
    return I*cos(w*t)

def visualize(u, t, I, w):
    plot(t, u, 'r--o')
    t_fine = linspace(0, t[-1], 1001)  # very fine mesh for u_e
    u_e = exact_solution(t_fine, I, w)
    hold('on')
    plot(t_fine, u_e, 'b-')
    legend(['numerical', 'exact'], loc='upper left')
    xlabel('t')
    ylabel('u')
    dt = t[1] - t[0]
    title('dt=%g' % dt)
    umin = 1.2*u.min();  umax = -umin
    axis([t[0], t[-1], umin, umax])
    savefig('vib1.png')
    savefig('vib1.pdf')
    savefig('vib1.eps')

Main program

I = 1
w = 2*pi
dt = 0.05
num_periods = 5
P = 2*pi/w    #  one period
T = P*num_periods
u, t = solver(I, w, dt, T)
visualize(u, t, I, w, dt)

User interface: command line

import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--I', type=float, default=1.0)
parser.add_argument('--w', type=float, default=2*pi)
parser.add_argument('--dt', type=float, default=0.05)
parser.add_argument('--num_periods', type=int, default=5)
a = parser.parse_args()
I, w, dt, num_periods = a.I, a.w, a.dt, a.num_periods

Running the program

vib_undamped.py:

Terminal> python vib_undamped.py --dt 0.05 --num_periods 40

Generates frames tmp_vib%04d.png in files. Can make movie:

Terminal> avconv -r 12 -i tmp_vib%04d.png -vcodec flv movie.flv

Can use ffmpeg instead of avconv.

Verification

First steps for testing and debugging

• Testing very simple solutions: \( u=\hbox{const} \) or \( u=ct + d \) do not apply here (without a force term in the equation: \( u'' + \omega^2u = f \)).
• Hand calculations: calculate \( u^1 \) and \( u^2 \) and compare with program.

Checking convergence rates

The next function estimates convergence rates, i.e., it

• performs \( m \) simulations with halved time steps: \( 2^{-k}\Delta t \), \( k=0,\ldots,m-1 \),
• computes the \( L_2 \) norm of the error, \( E = \sqrt{\Delta t_i\sum_{n=0}^{N_t-1}(u^n-\uex(t_n))^2} \) in each case,
• estimates the rates \( r_i \) from two consecutive experiments \( (\Delta t_{i-1}, E_{i-1}) \) and \( (\Delta t_{i}, E_{i}) \), assuming \( E_i=C\Delta t_i^{r_i} \) and \( E_{i-1}=C\Delta t_{i-1}^{r_i} \):

Implementational details

def convergence_rates(m, num_periods=8):
    """
    Return m-1 empirical estimates of the convergence rate
    based on m simulations, where the time step is halved
    for each simulation.
    """
    w = 0.35; I = 0.3
    dt = 2*pi/w/30  # 30 time step per period 2*pi/w
    T = 2*pi/w*num_periods
    dt_values = []
    E_values = []
    for i in range(m):
        u, t = solver(I, w, dt, T)
        u_e = exact_solution(t, I, w)
        E = sqrt(dt*sum((u_e-u)**2))
        dt_values.append(dt)
        E_values.append(E)
        dt = dt/2

    r = [log(E_values[i-1]/E_values[i])/
         log(dt_values[i-1]/dt_values[i])
         for i in range(1, m, 1)]
    return r

Result: r contains values equal to 2.00 - as expected!

Nose test

Use final r[-1] in a unit test:

def test_convergence_rates():
    r = convergence_rates(m=5, num_periods=8)
    # Accept rate to 1 decimal place
    nt.assert_almost_equal(r[-1], 2.0, places=1)

Complete code in vib_undamped.py.

Long time simulations

Effect of the time step on long simulations

• The numerical solution seems to have right amplitude.
• There is a phase error (reduced by reducing the time step).
• The total phase error seems to grow with time.

Using a moving plot window

• In long time simulations we need a plot window that follows the solution.
• Method 1: scitools.MovingPlotWindow.
• Method 2: scitools.avplotter (ASCII vertical plotter).

Example:

Terminal> python vib_undamped.py --dt 0.05 --num_periods 40

Movie of the moving plot window.

Analysis of the numerical scheme

Deriving an exact numerical solution; ideas

• Linear, homogeneous, difference equation for \( u^n \).
• Has solutions \( u^n \sim IA^n \), where \( A \) is unknown (number).
• Here: \( \uex(t) =I\cos(\omega t) \sim I\exp{(i\omega t)} = I(e^{i\omega\Delta t})^n \)
• Trick for simplifying the algebra: \( u^n = IA^n \), with \( A=\exp{(i\tilde\omega\Delta t)} \), then find \( \tilde\omega \)
• \( \tilde\omega \): unknown numerical frequency (easier to calculate than \( A \))
• \( \omega - \tilde\omega \) is the phase error
• Use the real part as the physical relevant part of a complex expression

Deriving an exact numerical solution; calculations (1)

 
$$ u^n = IA^n = I\exp{(\tilde\omega \Delta t\, n)}=I\exp{(\tilde\omega t)} = I\cos (\tilde\omega t) + iI\sin(\tilde \omega t) \tp $$

 
$$ \begin{align*} [D_tD_t u]^n &= \frac{u^{n+1} - 2u^n + u^{n-1}}{\Delta t^2}\\ &= I\frac{A^{n+1} - 2A^n + A^{n-1}}{\Delta t^2}\\ &= I\frac{\exp{(i\tilde\omega(t+\Delta t))} - 2\exp{(i\tilde\omega t)} + \exp{(i\tilde\omega(t-\Delta t))}}{\Delta t^2}\\ &= I\exp{(i\tilde\omega t)}\frac{1}{\Delta t^2}\left(\exp{(i\tilde\omega(\Delta t))} + \exp{(i\tilde\omega(-\Delta t))} - 2\right)\\ &= I\exp{(i\tilde\omega t)}\frac{2}{\Delta t^2}\left(\cosh(i\tilde\omega\Delta t) -1 \right)\\ &= I\exp{(i\tilde\omega t)}\frac{2}{\Delta t^2}\left(\cos(\tilde\omega\Delta t) -1 \right)\\ &= -I\exp{(i\tilde\omega t)}\frac{4}{\Delta t^2}\sin^2(\frac{\tilde\omega\Delta t}{2}) \end{align*} $$

Deriving an exact numerical; calculations (2)

The scheme (6) with \( u^n=I\exp{(i\omega\tilde\Delta t\, n)} \) inserted gives

 
$$ \begin{equation} -I\exp{(i\tilde\omega t)}\frac{4}{\Delta t^2}\sin^2(\frac{\tilde\omega\Delta t}{2}) + \omega^2 I\exp{(i\tilde\omega t)} = 0, \end{equation} $$

 
which after dividing by \( Io\exp{(i\tilde\omega t)} \) results in

 
$$ \begin{equation} \frac{4}{\Delta t^2}\sin^2(\frac{\tilde\omega\Delta t}{2}) = \omega^2 \tp \end{equation} $$

 
Solve for \( \tilde\omega \):

 
$$ \begin{equation} \tilde\omega = \pm \frac{2}{\Delta t}\sin^{-1}\left(\frac{\omega\Delta t}{2}\right) \tp \tag{9} \end{equation} $$

• Phase error because \( \tilde\omega \neq \omega \).
• But how good is the approximation \( \tilde\omega \) to \( \omega \)?

Polynomial approximation of the phase error

Taylor series expansion for small \( \Delta t \) gives a formula that is easier to understand:

>>> from sympy import *
>>> dt, w = symbols('dt w')
>>> w_tilde = asin(w*dt/2).series(dt, 0, 4)*2/dt
>>> print w_tilde
(dt*w + dt**3*w**3/24 + O(dt**4))/dt  # observe final /dt

 
$$ \begin{equation} \tilde\omega = \omega\left( 1 + \frac{1}{24}\omega^2\Delta t^2\right) + {\cal O}(\Delta t^3) \tp \tag{10} \end{equation} $$

 
The numerical frequency is too large (to fast oscillations).

Plot of the phase error

Recommendation: 25-30 points per period.

Exact discrete solution

 
$$ \begin{equation} u^n = I\cos\left(\tilde\omega n\Delta t\right),\quad \tilde\omega = \frac{2}{\Delta t}\sin^{-1}\left(\frac{\omega\Delta t}{2}\right) \tp \tag{11} \end{equation} $$

The error mesh function,

 
$$ e^n = \uex(t_n) - u^n = I\cos\left(\omega n\Delta t\right) - I\cos\left(\tilde\omega n\Delta t\right) $$

 
is ideal for verification and analysis.

Convergence of the numerical scheme

Can easily show convergence:

 
$$ e^n\rightarrow 0 \hbox{ as }\Delta t\rightarrow 0,$$

 
because

 
$$ \lim_{\Delta t\rightarrow 0} \tilde\omega = \lim_{\Delta t\rightarrow 0} \frac{2}{\Delta t}\sin^{-1}\left(\frac{\omega\Delta t}{2}\right) = \omega, $$

 
by L'Hopital's rule or simply asking (2/x)*asin(w*x/2) as x->0 in WolframAlpha.

Stability

Observations:

• Numerical solution has constant amplitude (desired!), but phase error.
• Constant amplitude requires \( \sin^{-1}(\omega\Delta t/2) \) to be real-valued \( \Rightarrow \) $|\omega\Delta t/2| \leq 1$.
• \( \sin^{-1}(x) \) is complex if \( |x|>1 \), and then \( \tilde\omega \) becomes complex.

What is the consequence of complex \( \tilde\omega \)?

• Set \( \tilde\omega = \tilde\omega_r + i\tilde\omega_i \).
• Since \( \sin^{-1}(x) \) has a negative* imaginary part for \( x>1 \), \( \exp{(i\omega\tilde t)}=\exp{(-\tilde\omega_i t)}\exp{(i\tilde\omega_r t)} \) leads to exponential growth \( e^{-\tilde\omega_it} \) when \( -\tilde\omega_i t > 0 \).
• This is instability because the qualitative behavior is wrong.

The stability criterion

Cannot tolerate growth and must therefore demand a stability criterion

 
$$ \begin{equation} \frac{\omega\Delta t}{2} \leq 1\quad\Rightarrow\quad \Delta t \leq \frac{2}{\omega} \tp \end{equation} $$

Try \( \Delta t = \frac{2}{\omega} + 9.01\cdot 10^{-5} \) (slightly too big!):

Summary of the analysis

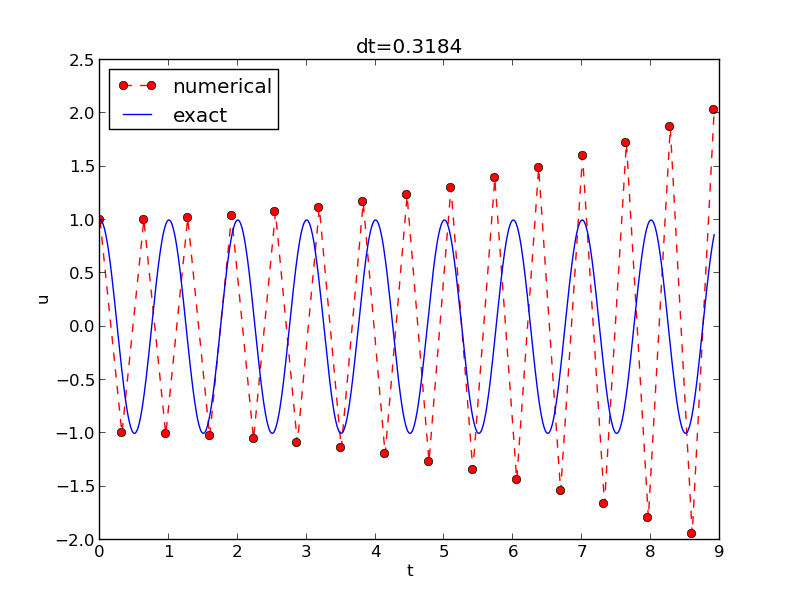
We can draw three important conclusions:

1. The key parameter in the formulas is \( p=\omega\Delta t \).

1. Period of oscillations: \( P=2\pi/\omega \)
2. Number of time steps per period: \( N_P=P/\Delta t \)
3. \( \Rightarrow\ p=\omega\Delta t = 2\pi/ N_P \sim 1/N_P \)
4. The smallest possible \( N_P \) is 2 \( \Rightarrow \) $p\in (0,\pi]$
2. For \( p\leq 2 \) the amplitude of \( u^n \) is constant (stable solution)
3. \( u^n \) has a relative phase error \( \tilde\omega/\omega \approx 1 + \frac{1}{24}p^2 \), making numerical peaks occur too early

Alternative schemes based on 1st-order equations

Rewriting 2nd-order ODE as system of two 1st-order ODEs

The vast collection of ODE solvers (e.g., in Odespy) cannot be applied to

 
$$ u'' + \omega^2 u = 0$$

 
unless we write this higher-order ODE as a system of 1st-order ODEs.

Introduce an auxiliary variable \( v=u' \):

 
$$ \begin{align} u' &= v, \tag{12}\\ v' &= -\omega^2 u \tag{13} \tp \end{align} $$

Initial conditions: \( u(0)=I \) and \( v(0)=0 \).

The Forward Euler scheme

We apply the Forward Euler scheme to each component equation:

 
$$ [D_t^+ u = v]^n,$$

 
$$ [D_t^+ v = -\omega^2 u]^n,$$

 
or written out,

 
$$ \begin{align} u^{n+1} &= u^n + \Delta t v^n,\\ v^{n+1} &= v^n -\Delta t \omega^2 u^n \tp \end{align} $$

The Backward Euler scheme

We apply the Backward Euler scheme to each component equation:

 
$$ [D_t^- u = v]^{n+1},$$

 
$$ [D_t^- v = -\omega u]^{n+1} \tp $$

 
Written out:

 
$$ \begin{align} u^{n+1} - \Delta t v^{n+1} = u^{n},\\ v^{n+1} + \Delta t \omega^2 u^{n+1} = v^{n} \tp \end{align} $$

 
This is a coupled \( 2\times 2 \) system for the new values at \( t=t_{n+1} \)!

The Crank-Nicolson scheme

 
$$ [D_t u = \overline{v}^t]^{n+\half},$$

 
$$ [D_t v = -\omega \overline{u}^t]^{n+\half}$$

 
The result is also a coupled system:

 
$$ \begin{align} u^{n+1} - \half\Delta t v^{n+1} &= u^{n} + \half\Delta t v^{n},\\ v^{n+1} + \half\Delta t \omega^2 u^{n+1} &= v^{n} - \half\Delta t \omega^2 u^{n} \tp \end{align} $$

Comparison of schemes via Odespy

Can use Odespy to compare many methods for first-order schemes:

import odespy
import numpy as np

def f(u, t, w=1):
    u, v = u  # u is array of length 2 holding our [u, v]
    return [v, -w**2*u]

def run_solvers_and_plot(solvers, timesteps_per_period=20,
                         num_periods=1, I=1, w=2*np.pi):
    P = 2*np.pi/w  # duration of one period
    dt = P/timesteps_per_period
    Nt = num_periods*timesteps_per_period
    T = Nt*dt
    t_mesh = np.linspace(0, T, Nt+1)

    legends = []
    for solver in solvers:
        solver.set(f_kwargs={'w': w})
        solver.set_initial_condition([I, 0])
        u, t = solver.solve(t_mesh)

Forward and Backward Euler and Crank-Nicolson

solvers = [
    odespy.ForwardEuler(f),
    # Implicit methods must use Newton solver to converge
    odespy.BackwardEuler(f, nonlinear_solver='Newton'),
    odespy.CrankNicolson(f, nonlinear_solver='Newton'),
    ]

Two plot types:

• \( u(t) \) vs \( t \)
• Parameterized curve \( (u(t), v(t)) \) in phase space
• Exact curve is an ellipse: \( (I\cos\omega t, -\omega I\sin\omega t) \), closed and periodic

Phase plane plot of the numerical solutions

Note: CrankNicolson in Odespy leads to the name MidpointImplicit in plots.

Plain solution curves

Observations from the figures

• Forward Euler has growing amplitude and outward \( (u,v) \) spiral - pumps energy into the system.
• Backward Euler is opposite: decreasing amplitude, inward sprial, extracts energy.
• Forward and Backward Euler are useless for vibrations.
• Crank-Nicolson (MidpointImplicit) looks much better.

Runge-Kutta methods of order 2 and 4; short time series

Runge-Kutta methods of order 2 and 4; longer time series

Crank-Nicolson; longer time series

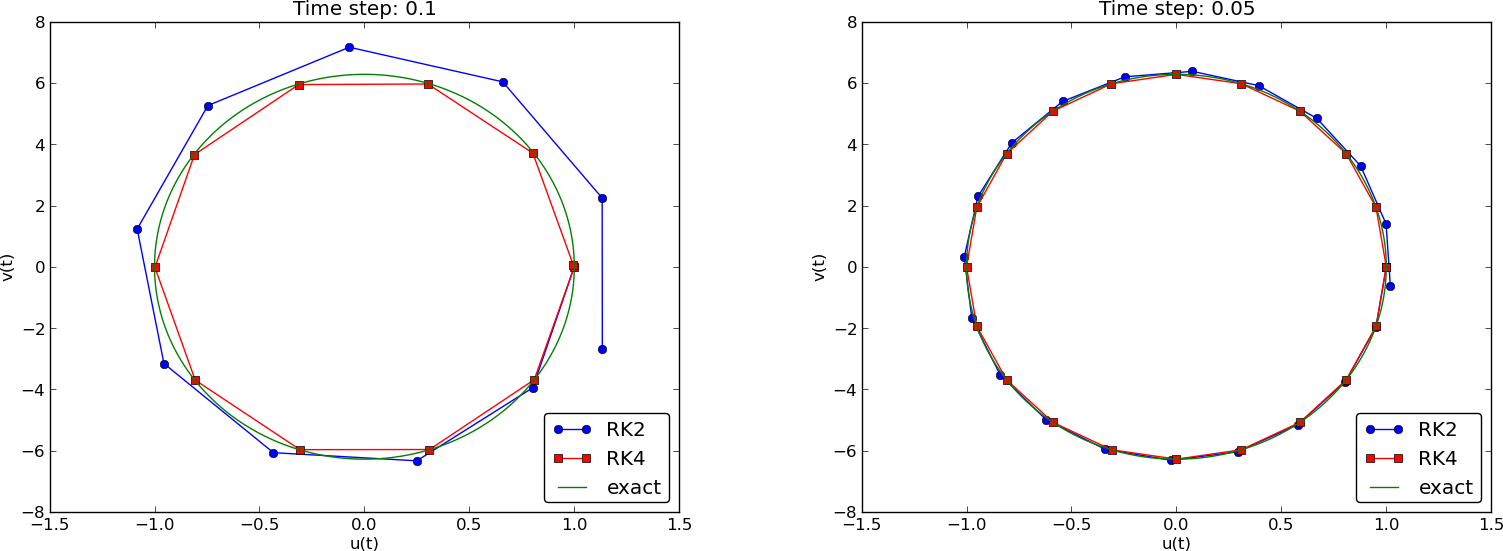
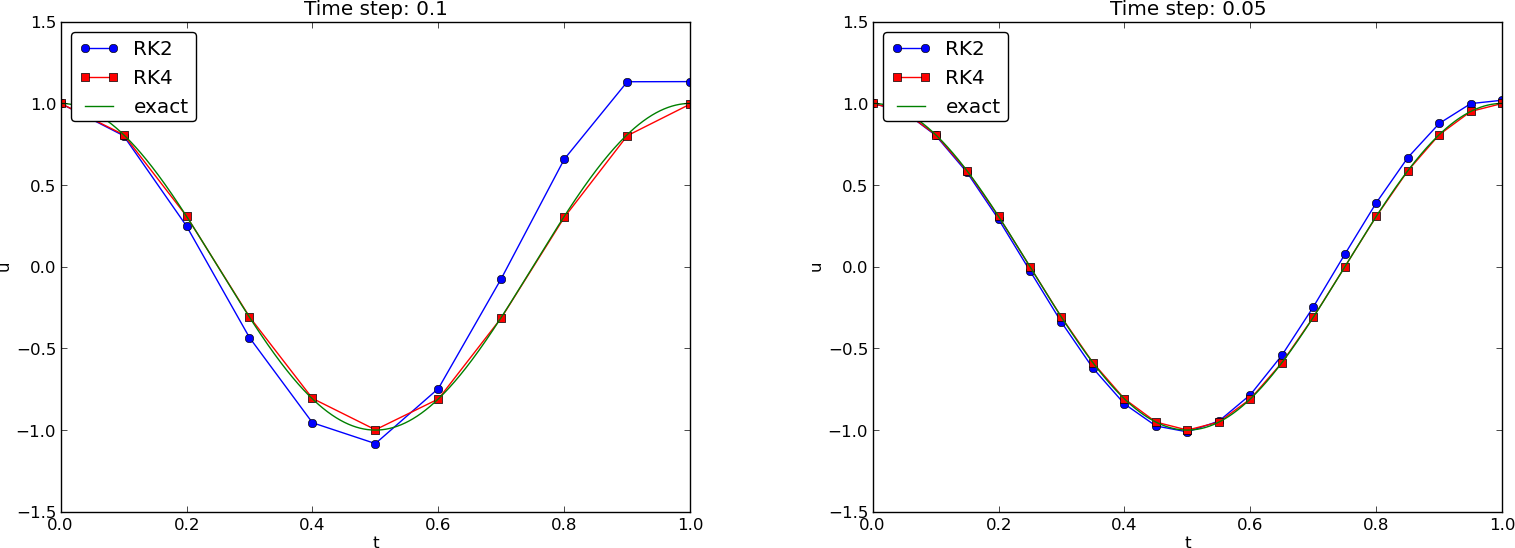
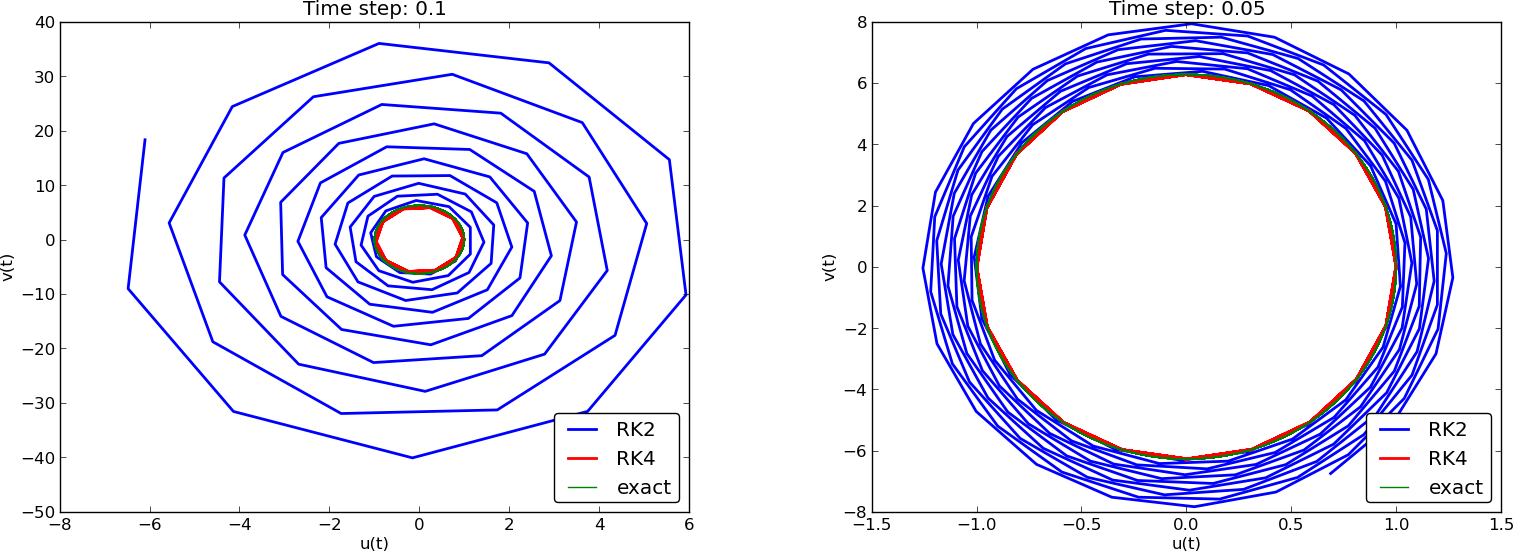
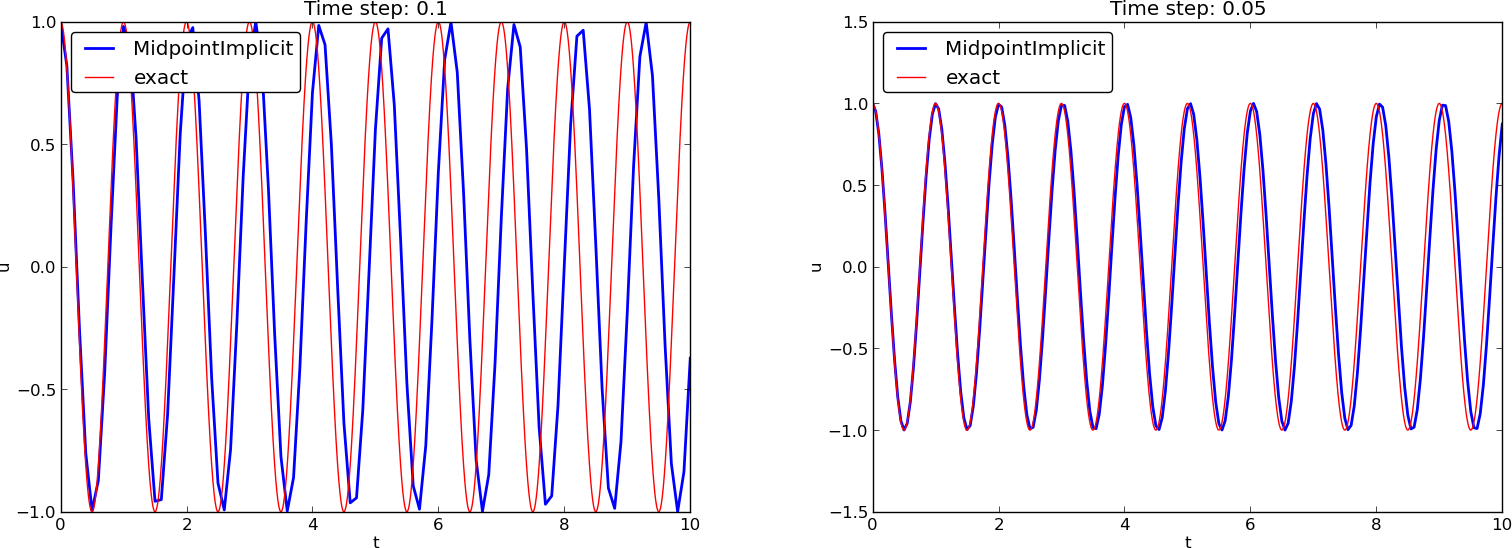
(MidpointImplicit means CrankNicolson in Odespy)

Observations of RK and CN methods

• 4th-order Runge-Kutta is very accurate, also for large \( \Delta t \).
• 2th-order Runge-Kutta is almost as bad as Forward and Backward Euler.
• Crank-Nicolson is accurate, but the amplitude is not as accurate as the difference scheme for \( u''+\omega^2u=0 \).

Energy conservation property

The model

 
$$ u'' + \omega^2 u = 0,\quad u(0)=I,\ u'(0)=V,$$

 
has the nice energy conservation property that

 
$$ E(t) = \half(u')^2 + \half\omega^2u^2 = \hbox{const}\tp$$

 
This can be used to check solutions.

Derivation of the energy conservation property

Multiply \( u''+\omega^2u=0 \) by \( u' \) and integrate:

 
$$ \int_0^T u''u' dt + \int_0^T\omega^2 u u' dt = 0\tp$$

 
Observing that

 
$$ u''u' = \frac{d}{dt}\half(u')^2,\quad uu' = \frac{d}{dt} {\half}u^2,$$

 
we get

 
$$ \int_0^T (\frac{d}{dt}\half(u')^2 + \frac{d}{dt} \half\omega^2u^2)dt = E(T) - E(0), $$

 
where

 
$$ \begin{equation} E(t) = \half(u')^2 + \half\omega^2u^2\tp \tag{14} \end{equation} $$

Remark about \( E(t) \)

\( E(t) \) does not measure energy, energy per mass unit.

Starting with an ODE coming directly from Newton's 2nd law \( F=ma \) with a spring force \( F=-ku \) and \( ma=mu'' \) (\( a \): acceleration, \( u \): displacement), we have

 
$$ mu'' + ku = 0$$

 
Integrating this equation gives a physical energy balance:

 
$$ E(t) = \underbrace{{\half}mv^2}_{\hbox{kinetic energy} } + \underbrace{{\half}ku^2}_{\hbox{potential energy}} = E(0),\quad v=u' $$

 
Note: the balance is not valid if we add other terms to the ODE.

The Euler-Cromer method; idea

Forward-backward discretization of the 2x2 system:

• Update \( u \) with Forward Euler
• Update \( v \) with Backward Euler, using latest \( u \)

 
$$ [D_t^+u = v]^n,$$

 
$$ [D_t^-v = -\omega u]^{n+1} \tp $$

The Euler-Cromer method; complete formulas

Written out:

 
$$ \begin{align} u^0 &= I,\\ v^0 &= 0,\\ u^{n+1} &= u^n + \Delta t v^n, \tag{15}\\ v^{n+1} &= v^n -\Delta t \omega^2u^{n+1} \tag{16} \tp \end{align} $$

Names: Forward-backward scheme, Semi-implicit Euler method, symplectic Euler, semi-explicit Euler, Newton-Stormer-Verlet, and Euler-Cromer.

• Forward Euler and Backward Euler have error \( \Oof{\Delta t} \)
• What about the overall scheme? Expect \( \Oof{\Delta t} \)...

Equivalence with the scheme for the second-order ODE

Goal: eliminate \( v^n \). We have

 
$$ v^n = v^{n-1} - \Delta t \omega^2u^{n}, $$

 
which can be inserted in (15) to yield

 
$$ \begin{equation} u^{n+1} = u^n + \Delta t v^{n-1} - \Delta t^2 \omega^2u^{n} . \tag{17} \end{equation} $$

 
Using (15),

 
$$ v^{n-1} = \frac{u^n - u^{n-1}}{\Delta t}, $$

 
and when this is inserted in (17) we get

 
$$ \begin{equation} u^{n+1} = 2u^n - u^{n-1} - \Delta t^2 \omega^2u^{n} \end{equation} $$

Comparison of the treatment of initial conditions

• The Euler-Cromer scheme is nothing but the centered scheme for \( u''+\omega^2u=0 \) (6)!
• The previous analysis of this scheme then also applies to the Euler-Cromer method!
• What about the initial conditions?

 
$$ u'=v=0\quad\Rightarrow\quad v^0=0,$$

 
and (15) implies \( u^1=u^0 \), while (16) says \( v^1=-\omega^2 u^0 \).

This \( u^1=u^0 \) approximation corresponds to a first-order Forward Euler discretization of \( u'(0)=0 \): \( [D_t^+ u = 0]^0 \).

A method utilizing a staggered mesh

• The Euler-Cromer scheme uses two unsymmetric differences in a symmetric way...
• We can derive the method from a more pedagogical point of view where we use a staggered mesh and only centered differences

Staggered mesh:

• \( u \) is unknown at mesh points \( t_0,t_1,\ldots,t_n,\ldots \)
• \( v \) is unknown at mesh points \( t_{1/2}, t_{3/2},\ldots, t_{n+1/2},\ldots \) (between the \( u \) points)

Centered differences on a staggered mesh

 
$$ \begin{align} \lbrack D_t u &= v\rbrack^{n+\half},\\ \lbrack D_t v &= -\omega u\rbrack^{n+1} \tp \end{align} $$

 
Written out:

 
$$ \begin{align} u^{n+1} &= u^{n} + \Delta t v^{n+\half}, \tag{18}\\ v^{n+\frac{3}{2}} &= v^{n+\half} -\Delta t \omega^2u^{n+1} \tag{19} \tp \end{align} $$

 
or shift one time level back (purely of esthetic reasons):

 
$$ \begin{align} u^{n} &= u^{n-1} + \Delta t v^{n-\half}, \tag{20}\\ v^{n+\half} &= v^{n-\half} -\Delta t \omega^2u^{n} \tag{21} \tp \end{align} $$

Comparison with the scheme for the 2nd-order ODE

• Can eliminate \( v^{n\pm 1/2} \) and get the centered scheme for \( u''+\omega^2 u = 0 \)
• What about the initial conditions? Their equivalent too!

\( u(0)=0 \) and \( u'(0)=v(0)=0 \) give \( u^0=I \) and

 
$$ v(0)\approx \half(v^{-\half} + v^{\half}) = 0, \quad\Rightarrow\quad v^{-\half} =- v^\half\tp$$

 
Combined with the scheme on the staggered mesh we get

 
$$ u^1 = u^0 - \half\Delta t^2\omega^2 I,$$

Implementation of a staggered mesh; integer indices

• How to write \( v^{n+\half} \) in the code? v[i+0.5] does not work...
• Need a storage convention:

• \( v^{1+\half} \) $\rightarrow$ v[n]
• \( v^{1-\half} \) $\rightarrow$ v[n-1]
• \( v^{n+\half} = v^{n-\half} -\Delta t \omega^2u^{n} \) becomes v[n] = v[n-1] - dt*w**2*u[n]

!bc pycod
def solver(I, w, dt, T):
    # set up variables...

    u[0] = I
    v[0] = 0 - 0.5*dt*w**2*u[0]
    for n in range(1, Nt+1):
        u[n] = u[n-1] + dt*v[n-1]
        v[n] = v[n-1] - dt*w**2*u[n]
    return u, t, v, t_v

Implementation of a staggered mesh; half-integer indices (1)

It would be nice to write

 
$$ \begin{align*} u^{n} &= u^{n-1} + \Delta t v^{n-\half},\\ v^{n+\half} &= v^{n-\half} -\Delta t \omega^2u^{n}, \end{align*} $$

 
as

u[n] = u[n-1] + dt*v[n-half]
v[n+half] = v[n-half] - dt*w**2*u[n]

(Implying that n+half is n and n-half is n-1.)

Implementation of a staggered mesh; half-integer indices (2)

This class ensures that n+half is n and n-half is n-1:

class HalfInt:
    def __radd__(self, other):
        return other

    def __rsub__(self, other):
        return other - 1

half = HalfInt()

Now

u[n] = u[n-1] + dt*v[n-half]
v[n+half] = v[n-half] - dt*w**2*u[n]

is equivalent to

u[n] = u[n-1] + dt*v[n-1]
v[n] = v[n-1] - dt*w**2*u[n]

Generalization: damping, nonlinear spring, and external excitation

 
$$ \begin{equation} mu'' + f(u') + s(u) = F(t),\quad u(0)=I,\ u'(0)=V,\ t\in (0,T] \tp \tag{22} \end{equation} $$

 
Input data: \( m \), \( f(u') \), \( s(u) \), \( F(t) \), \( I \), \( V \), and \( T \).

Typical choices of \( f \) and \( s \):

• linear damping \( f(u')=bu \), or
• quadratic damping \( f(u')=bu'|u'| \)
• linear spring \( s(u)=cu \)
• nonlinear spring \( s(u)\sim \sin(u) \) (pendulum)

A centered scheme for linear damping

 
$$ \begin{equation} [mD_tD_t u + f(D_{2t}u) + s(u) = F]^n \end{equation} $$

 
Written out

 
$$ \begin{equation} m\frac{u^{n+1}-2u^n + u^{n-1}}{\Delta t^2} + f(\frac{u^{n+1}-u^{n-1}}{2\Delta t}) + s(u^n) = F^n \tag{23} \end{equation} $$

 
Assume \( f(u') \) is linear in \( u'=v \):

 
$$ \begin{equation} u^{n+1} = \left(2mu^n + (\frac{b}{2}\Delta t - m)u^{n-1} + \Delta t^2(F^n - s(u^n)) \right)(m + \frac{b}{2}\Delta t)^{-1} \tag{24} \tp \end{equation} $$

Initial conditions

\( u(0)=I \), \( u'(0)=V \):

 
$$ \begin{align} \lbrack u &=I\rbrack^0\quad\Rightarrow\quad u^0=I,\\ \lbrack D_{2t}u &=V\rbrack^0\quad\Rightarrow\quad u^{-1} = u^{1} - 2\Delta t V \end{align} $$

 
End result:

 
$$ \begin{equation} u^1 = u^0 + \Delta t\, V + \frac{\Delta t^2}{2m}(-bV - s(u^0) + F^0) \tp \tag{25} \end{equation} $$

 
Same formula for \( u^1 \) as when using a centered scheme for \( u''+\omega u=0 \).

Linearization via a geometric mean approximation

• \( f(u')=bu'|u'| \) leads to a quadratic equation for \( u^{n+1} \)
• Instead of solving the quadratic equation, we use a geometric mean approximation

In general, the geometric mean approximation reads

 
$$ (w^2)^n \approx w^{n-\half}w^{n+\half}\tp$$

 
For \( |u'|u' \) at \( t_n \):

 
$$ [u'|u'|]^n \approx u'(t_n+{\half})|u'(t_n-{\half})|\tp$$

 
For \( u' \) at \( t_{n\pm 1/2} \) we use centered difference:

 
$$ \begin{equation} u'(t_{n+1/2})\approx [D_t u]^{n+\half},\quad u'(t_{n-1/2})\approx [D_t u]^{n-\half} \tp \tag{26} \end{equation} $$

A centered scheme for quadratic damping

After some algebra:

 
$$ \begin{align} u^{n+1} &= \left( m + b|u^n-u^{n-1}|\right)^{-1}\times \nonumber\\ & \qquad \left(2m u^n - mu^{n-1} + bu^n|u^n-u^{n-1}| + \Delta t^2 (F^n - s(u^n)) \right) \tp \tag{27} \end{align} $$

Initial condition for quadratic damping

Simply use that \( u'=V \) in the scheme when \( t=0 \) (\( n=0 \)):

 
$$ \begin{equation} [mD_tD_t u + bV|V| + s(u) = F]^0 \end{equation} $$

which gives

 
$$ \begin{equation} u^1 = u^0 + \Delta t V + \frac{\Delta t^2}{2m}\left(-bV|V| - s(u^0) + F^0\right) \tp \tag{28} \end{equation} $$

Algorithm

1. \( u^0=I \)
2. compute \( u^1 \) from (25) if linear damping or (28) if quadratic damping
3. for \( n=1,2,\ldots,N_t-1 \):

1. compute \( u^{n+1} \) from (24) if linear damping or (27) if quadratic damping

Implementation

def solver(I, V, m, b, s, F, dt, T, damping='linear'):
    dt = float(dt); b = float(b); m = float(m) # avoid integer div.
    Nt = int(round(T/dt))
    u = zeros(Nt+1)
    t = linspace(0, Nt*dt, Nt+1)

    u[0] = I
    if damping == 'linear':
        u[1] = u[0] + dt*V + dt**2/(2*m)*(-b*V - s(u[0]) + F(t[0]))
    elif damping == 'quadratic':
        u[1] = u[0] + dt*V + \ 
               dt**2/(2*m)*(-b*V*abs(V) - s(u[0]) + F(t[0]))

    for n in range(1, Nt):
        if damping == 'linear':
            u[n+1] = (2*m*u[n] + (b*dt/2 - m)*u[n-1] +
                      dt**2*(F(t[n]) - s(u[n])))/(m + b*dt/2)
        elif damping == 'quadratic':
            u[n+1] = (2*m*u[n] - m*u[n-1] + b*u[n]*abs(u[n] - u[n-1])
                      + dt**2*(F(t[n]) - s(u[n])))/\ 
                      (m + b*abs(u[n] - u[n-1]))
    return u, t

Verification

• Constant solution \( \uex = I \) (\( V=0 \)) fulfills the ODE problem and the discrete equations. Ideal for debugging!
• Linear solution \( \uex = Vt+I \) fulfills the ODE problem and the discrete equations.
• Quadratic solution \( \uex = bt^2 + Vt + I \) fulfills the ODE problem and the discrete equations with linear damping, but not for quadratic damping. A special discrete source term can allow \( \uex \) to also fulfill the discrete equations with quadratic damping.

Demo program

vib.py supports input via the command line:

Terminal> python vib.py --s 'sin(u)' --F '3*cos(4*t)' --c 0.03

This results in a moving window following the function on the screen.

Euler-Cromer formulation

We rewrite

 
$$ \begin{equation} mu'' + f(u') + s(u) = F(t),\quad u(0)=I,\ u'(0)=V,\ t\in (0,T], \end{equation} $$

 
as a first-order ODE system

 
$$ \begin{align} u' &= v, \tag{29} \\ v' &= m^{-1}\left(F(t) - f(v) - s(u)\right)\tp \tag{30} \end{align} $$

Staggered grid

• \( u \) is unknown at \( t_n \): \( u^n \)
• \( v \) is unknown at \( t_{n+1/2} \): \( v^{n+\half} \)
• All derivatives are approximated by centered differences

 
$$ \begin{align} \lbrack D_t u &= v\rbrack^{n-\half}, \tag{31} \\ \lbrack D_tv &= m^{-1}\left(F(t) - f(v) - s(u)\right)\rbrack^n\tp \tag{32} \end{align} $$

Written out,

 
$$ \begin{align} \frac{u^n - u^{n-1}}{\Delta t} &= v^{n-\half}, \tag{33} \\ \frac{v^{n+\half} - v^{n-\half}}{\Delta t} &= m^{-1}\left(F^n - f(v^n) - s(u^n)\right)\tp \tag{34} \end{align} $$

Problem: \( f(v^n) \)

Linear damping

With \( f(v)=bv \), we can use an arithmetic mean for \( bv^n \) a la Crank-Nicolson schemes.

 
$$ \begin{align*} u^n & = u^{n-1} + {\Delta t}v^{n-\half},\\ v^{n+\half} &= \left(1 + \frac{b}{2m}\Delta t\right)^{-1}\left( v^{n-\half} + {\Delta t} m^{-1}\left(F^n - {\half}f(v^{n-\half}) - s(u^n)\right)\right)\tp \end{align*} $$

Quadratic damping

With \( f(v)=b|v|v \), we can use a geometric mean

 
$$ b|v^n|v^n\approx b|v^{n-\half}|v^{n+\half}, $$

 
resulting in

 
$$ \begin{align*} u^n & = u^{n-1} + {\Delta t}v^{n-\half},\\ v^{n+\half} &= (1 + \frac{b}{m}|v^{n-\half}|\Delta t)^{-1}\left( v^{n-\half} + {\Delta t} m^{-1}\left(F^n - s(u^n)\right)\right)\tp \end{align*} $$

Initial conditions

 
$$ \begin{align} u^0 &= I, \tag{35}\\ v^{\half} &= V - \half\Delta t\omega^2I \tag{36}\tp \end{align} $$