Empirical verification of the truncation error in the Forward Euler scheme
Figure 1: Estimated truncation error at mesh points for different meshes.

Overview of what truncation errors are
Abstract problem setting
Various error measures
Truncation errors in finite difference formulas
Example: The backward difference for \( u'(t) \)
Taylor series
Taylor series inserted in the backward difference approximation
The forward difference for \( u'(t) \)
The central difference for \( u'(t) \) (1)
The central difference for \( u'(t) \) (1)
Leading-order error terms in finite differences (1)
Leading-order error terms in finite differences (2)
Leading-order error terms in mean values (1)
Leading-order error terms in mean values (2)
Software for computing truncation errors
Symbolic computing with difference operators
Truncation errors in exponential decay ODE
Truncation error of the Forward Euler scheme
Truncation error of the Crank-Nicolson scheme
Test the understanding!
Truncation error of the \( \theta \)-rule
Using symbolic software
Empirical verification of the truncation error (1)
Empirical verification of the truncation error (2)
Empirical verification of the truncation error in the Forward Euler scheme
Empirical verification of the truncation error in the Forward Euler scheme
Increasing the accuracy by adding correction terms
Lowering the order of the derivative in the correction term
With a correction term Forward Euler becomes Crank-Nicolson
Correction terms in the Crank-Nicolson scheme (1)
Correction terms in the Crank-Nicolson scheme (2)
Extension to variable coefficients
Exact solutions of the finite difference equations
Computing truncation errors in nonlinear problems (1)
Computing truncation errors in nonlinear problems (2)
Truncation errors in vibration ODEs
Linear model without damping
Truncation errors in the initial condition
Computing correction terms
Model with damping and nonlinearity
Carrying out the truncation error analysis
Extension to quadratic damping
The truncation error for quadratic damping (1)
The truncation error for quadratic damping (2)
The general model formulated as first-order ODEs
The forward-backward scheme
Truncation error analysis
A centered scheme on a staggered mesh
Truncation error analysis (1)
Truncation error analysis (2)
Consider an abstract differential equation
$$ \mathcal{L}(u)=0\tp$$
Example: \( \mathcal{L}(u)=u'(t)+a(t)u(t)-b(t) \).
The corresponding discrete equation:
$$ \mathcal{L}_{\Delta}(u) =0\tp$$
Let now
$$
\begin{align*}
\mathcal{L}(\uex)&=0,\\
\mathcal{L}_\Delta(u)&=0\tp
\end{align*}
$$
\( u \) is computed at mesh points
Backward difference approximation to \( u' \):
$$
\begin{equation}
\lbrack D_t^- u\rbrack^n = \frac{u^{n} - u^{n-1}}{\Delta t} \approx u'(t_n)
\tag{1}
\tp
\end{equation}
$$
Define the truncation error of this approximation as
$$
\begin{equation}
R^n = [D^-_tu]^n - u'(t_n)\tp
\tag{2}
\end{equation}
$$
The common way of calculating \( R^n \) is to
General Taylor series expansion from calculus:
$$ f(x+h) = \sum_{i=0}^\infty \frac{1}{i!}\frac{d^if}{dx^i}(x)h^i\tp $$
Here: expand \( u^{n-1} \) around \( t_n \):
$$
\begin{align*}
u(t_{n-1}) = u(t-\Delta t) &= \sum_{i=0}^\infty \frac{1}{i!}\frac{d^iu}{dt^i}(t_n)(-\Delta t)^i\\
& = u(t_n) - u'(t_n)\Delta t + {\half}u''(t_n)\Delta t^2
+ \Oof{\Delta t^3},
\end{align*}
$$
$$
\begin{align*}
[D_t^-u]^n - u'(t_n) &= \frac{u(t_n) - u(t_{n-1})}{\Delta t} - u'(t_n)\\
&= \frac{u(t_n) - (u(t_n) - u'(t_n)\Delta t + {\half}u''(t_n)\Delta t^2 + \Oof{\Delta t^3} )}{\Delta t}\\
&\quad -u'(t_n)\\
&= -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2} )
\end{align*}
$$
Result:
$$
\begin{equation}
R^n = -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2} )
\tp
\end{equation}
$$
The difference approximation is of
first order in \( \Delta t \). It is exact for linear \( \uex \).
Now consider a forward difference:
$$ u'(t_n) \approx [D_t^+ u]^n = \frac{u^{n+1}-u^n}{\Delta t}\tp$$
Define the truncation error:
$$ R^n = [D_t^+ u]^n - u'(t_n)\tp$$
Expand \( u^{n+1} \) in a Taylor series around \( t_n \),
$$ u(t_{n+1}) = u(t_n) + u'(t_n)\Delta t +
{\half}u''(t_n)\Delta t^2 + \Oof{\Delta t^3}
\tp $$
We get
$$ R = {\half}u''(t_n)\Delta t +
\Oof{\Delta t^2}\tp$$
For the central difference approximation,
$$ u'(t_n)\approx [ D_tu]^n, \quad [D_tu]^n =
\frac{u^{n+\half} - u^{n-\half}}{\Delta t},
$$
the truncation error is
$$ R^n = [ D_tu]^n - u'(t_n)\tp$$
Expand \( u(t_{n+\half}) \) and
\( u(t_{n-1/2}) \) in Taylor series around the point \( t_n \) where
the derivative is evaluated:
$$
\begin{align*}
u(t_{n+\half}) = &u(t_n) + u'(t_n)\half\Delta t +
{\half}u''(t_n)(\half\Delta t)^2 + \\
& \frac{1}{6}u'''(t_n) (\half\Delta t)^3
+ \frac{1}{24}u''''(t_n) (\half\Delta t)^4 + \Oof{\Delta t^5}\\
u(t_{n-1/2}) = &u(t_n) - u'(t_n)\half\Delta t +
{\half}u''(t_n)(\half\Delta t)^2 - \\
& \frac{1}{6}u'''(t_n) (\half\Delta t)^3
+ \frac{1}{24}u''''(t_n) (\half\Delta t)^4 + \Oof{\Delta t^5}
\tp
\end{align*}
$$
$$
u(t_{n+\half}) - u(t_{n-1/2}) = u'(t_n)\Delta t + \frac{1}{24}u'''(t_n) \Delta t^3 + \Oof{\Delta t^5}
\tp
$$
By collecting terms in \( [D_t u]^n - u(t_n) \) we find \( R^n \) to be
$$
\begin{equation}
R^n = \frac{1}{24}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4},
\end{equation}
$$
Note:
$$
\begin{align}
\lbrack D_tu \rbrack^n &= \frac{u^{n+\half} - u^{n-\half}}{\Delta t} = u'(t_n) + R^n
\tag{3},\\
R^n &= \frac{1}{24}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{4}\\
\lbrack D_{2t}u \rbrack^n &= \frac{u^{n+1} - u^{n-1}}{2\Delta t} = u'(t_n) + R^n
\tag{5},\\
R^n &= \frac{1}{6}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{6}\\
\lbrack D_t^-u \rbrack^n &= \frac{u^{n} - u^{n-1}}{\Delta t} = u'(t_n) + R^n
\tag{7},\\
R^n &= -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{8}\\
\lbrack D_t^+u \rbrack^n &= \frac{u^{n+1} - u^{n}}{\Delta t} = u'(t_n) + R^n
\tag{9},\\
R^n &= {\half}u''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{10}
\end{align}
$$
$$
\begin{align}
[\bar D_tu]^{n+\theta} &= \frac{u^{n+1} - u^{n}}{\Delta t} = u'(t_{n+\theta}) + R^{n+\theta}
\tag{11},\\
R^{n+\theta} &= \half(1-2\theta)u''(t_{n+\theta})\Delta t -
\frac{1}{6}((1 - \theta)^3 - \theta^3)u'''(t_{n+\theta})\Delta t^2 +
\Oof{\Delta t^3}
\tag{12}\\
\lbrack D_t^{2-}u \rbrack^n &= \frac{3u^{n} - 4u^{n-1} + u^{n-2}}{2\Delta t} = u'(t_n) + R^n
\tag{13},\\
R^n &= -\frac{1}{3}u'''(t_n)\Delta t^2 + \Oof{\Delta t^3}
\tag{14}\\
\lbrack D_tD_t u \rbrack^n &= \frac{u^{n+1} - 2u^{n} + u^{n-1}}{\Delta t^2} = u''(t_n) + R^n
\tag{15},\\
R^n &= \frac{1}{12}u''''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{16}
\end{align}
$$
Weighted arithmetic mean:
$$
\begin{align}
[\overline{u}^{t,\theta}]^{n+\theta}
& = \theta u^{n+1} + (1-\theta)u^n =
u(t_{n+\theta}) + R^{n+\theta},
\tag{17}\\
R^{n+\theta} &= {\half}u''(t_{n+\theta})\Delta t^2\theta (1-\theta) +
\Oof{\Delta t^3}
\tp
\tag{18}
\end{align}
$$
Standard arithmetic mean:
$$
\begin{align}
[\overline{u}^{t}]^{n} &= \half(u^{n-\half} + u^{n+\half})
= u(t_n) + R^{n},
\tag{19}\\
R^{n} &= \frac{1}{8}u''(t_{n})\Delta t^2 + \frac{1}{384}u''''(t_n)\Delta t^4
+ \Oof{\Delta t^6}\tp
\tag{20}
\end{align}
$$
Geometric mean:
$$
\begin{align}
[\overline{u^2}^{t,g}]^{n} &= u^{n-\half}u^{n+\half} = (u^n)^2 + R^n,
\tag{21}\\
R^n &= - \frac{1}{4}u'(t_n)^2\Delta t^2 + \frac{1}{4}u(t_n)u''(t_n)\Delta t^2
+ \Oof{\Delta t^4}
\tp
\tag{22}
\end{align}
$$
Harmonic mean:
$$
\begin{align}
[\overline{u}^{t,h}]^{n} &= u^n = \frac{2}{\frac{1}{u^{n-\half}} + \frac{1}{u^{n+\half}}}
+ R^{n+\half},
\tag{23}\\
R^n &= - \frac{u'(t_n)^2}{4u(t_n)}\Delta t^2 + \frac{1}{8}u''(t_n)\Delta t^2
\tp
\tag{24}
\end{align}
$$
sympy to automate calculations with Taylor series.truncation_errors
>>> from truncation_errors import TaylorSeries
>>> from sympy import *
>>> u, dt = symbols('u dt')
>>> u_Taylor = TaylorSeries(u, 4)
>>> u_Taylor(dt)
D1u*dt + D2u*dt**2/2 + D3u*dt**3/6 + D4u*dt**4/24 + u
>>> FE = (u_Taylor(dt) - u)/dt
>>> FE
(D1u*dt + D2u*dt**2/2 + D3u*dt**3/6 + D4u*dt**4/24)/dt
>>> simplify(FE)
D1u + D2u*dt/2 + D3u*dt**2/6 + D4u*dt**3/24
Notation: D1u for \( u' \), D2u for \( u'' \), etc.
See trunc/truncation_errors.py.
A class DiffOp represents many common difference operators:
>>> from truncation_errors import DiffOp
>>> from sympy import *
>>> u = Symbol('u')
>>> diffop = DiffOp(u, independent_variable='t')
>>> diffop['geometric_mean']
-D1u**2*dt**2/4 - D1u*D3u*dt**4/48 + D2u**2*dt**4/64 + ...
>>> diffop['Dtm']
D1u + D2u*dt/2 + D3u*dt**2/6 + D4u*dt**3/24
>>> diffop.operator_names()
['geometric_mean', 'harmonic_mean', 'Dtm', 'D2t', 'DtDt',
'weighted_arithmetic_mean', 'Dtp', 'Dt']
Names in diffop:
Dtp for \( D^+_t \), Dtm for \( D_t^- \), Dt for \( D_t \), D2t for
\( D_{2t} \), DtDt for \( D_tD_t \).
$$
u'(t)=-au(t)
$$
The Forward Euler scheme:
$$
\begin{equation}
\lbrack D_t^+ u = -au \rbrack^n
\tag{25}
\tp
\end{equation}
$$
Definition of the truncation error \( R^n \):
$$
\begin{equation}
\lbrack D_t^+ \uex + a\uex = R \rbrack^n
\tag{26}
\tp
\end{equation}
$$
$$ [D_t^+ \uex]^n = \uex'(t_n) +
\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}\tp$$
Inserted in (26):
$$
\uex'(t_n) +
\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
+ a\uex(t_n) = R^n
\tp
$$
Note: \( \uex'(t_n) + a\uex^n = 0 \) since \( \uex \) solves the ODE. Then
$$
\begin{equation}
R^n = \half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{27}
\tp
\end{equation}
$$
Crank-Nicolson:
$$
\begin{equation}
[D_t u = -au]^{n+\half},
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_t \uex + a\overline{\uex}^{t} = R]^{n+\half}
\tp
\tag{28}
\end{equation}
$$
$$
\begin{align*}
\lbrack D_t\uex \rbrack^{n+\half} &= u'(t_{n+\half}) +
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2 + \Oof{\Delta t^4},\\
[a\overline{\uex}^{t}]^{n+\half}
&= u(t_{n+\half}) + \frac{1}{8}u''(t_{n})\Delta t^2 +
+ \Oof{\Delta t^4}
\end{align*}
$$
Inserted in the scheme we get
$$
\begin{equation}
R^{n+\half} = \left(
\frac{1}{24}\uex'''(t_{n+\half}) + \frac{1}{8}u''(t_{n})
\right)\Delta t^2 + \Oof{\Delta t^4}
\end{equation}
$$
\( R^n = \Oof{\Delta t^2} \) (second-order scheme)
Analyze the the truncation error of the Backward Euler scheme and show that it is \( \Oof{\Delta t} \) (first order scheme).
The \( \theta \)-rule:
$$
[\bar D_t u = -a\overline{u}^{t,\theta}]^{n+\theta}
\tp
$$
Truncation error:
$$
[\bar D_t \uex + a\overline{\uex}^{t,\theta} = R]^{n+\theta}
\tp
$$
Use (11)-(12) and (17)-(18) along with
\( \uex'(t_{n+\theta}) + a\uex(t_{n+\theta})=0 \) to show
$$
\begin{align}
R^{n+\theta}
=
&({\half}-\theta)\uex''(t_{n+\theta})\Delta t +
\half\theta (1-\theta)\uex''(t_{n+\theta})\Delta t^2 + \nonumber\\
& \half(\theta^2 -\theta + 3)\uex'''(t_{n+\theta})\Delta t^2
+ \Oof{\Delta t^3}
\end{align}
$$
Note: 2nd-order scheme if and only if \( \theta =1/2 \).
Can use sympy and the tools in
truncation_errors.py:
def decay():
u, a = sm.symbols('u a')
diffop = DiffOp(u, independent_variable='t',
num_terms_Taylor_series=3)
D1u = diffop.D(1) # symbol for du/dt
ODE = D1u + a*u # define ODE
# Define schemes
FE = diffop['Dtp'] + a*u
CN = diffop['Dt' ] + a*u
BE = diffop['Dtm'] + a*u
# Residuals (truncation errors)
R = {'FE': FE-ODE, 'BE': BE-ODE, 'CN': CN-ODE}
return R
The returned dictionary becomes
decay: {
'BE': D2u*dt/2 + D3u*dt**2/6,
'FE': -D2u*dt/2 + D3u*dt**2/6,
'CN': D3u*dt**2/24,
}
\( \theta \)-rule: see truncation_errors.py (long expression, very advantageous
to automate the math!)
Ideas:
For the Forward Euler scheme:
$$
\begin{equation}
R^n = \lbrack D_t^+\uex + a\uex \rbrack^n
\tag{29}
\tp
\end{equation}
$$
Insert correct \( \uex(t)=Ie^{-at} \) (or use method of manufactured solution
in more general cases).
See the text for more details and an implementation.
Figure 1: Estimated truncation error at mesh points for different meshes.

Figure 2: Difference between theoretical and estimated truncation error at mesh points for different meshes.
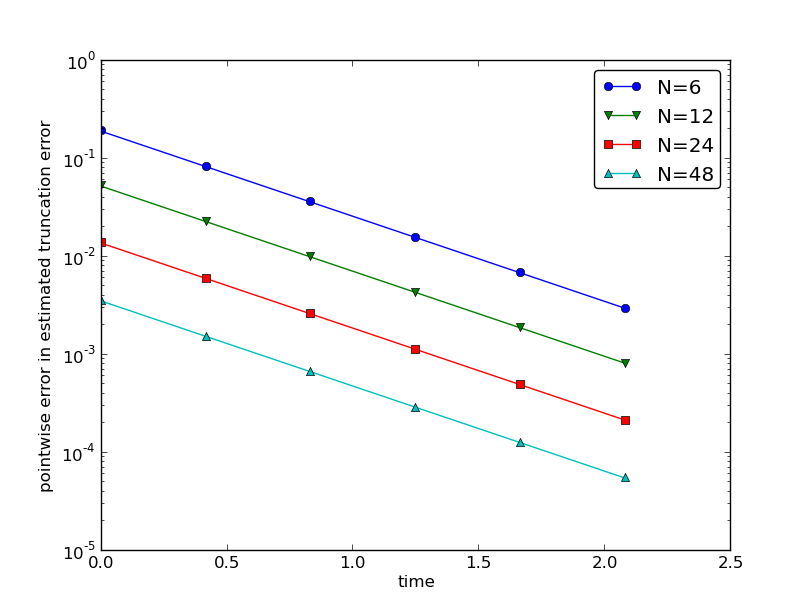
To be precise for the Forward Euler scheme, can we find \( C \) to make \( R \) $\Oof{\Delta t^2}$?
$$
\begin{equation}
\lbrack D_t^+ \uex + a\uex = C + R \rbrack^n\tp
\tag{30}
\end{equation}
$$
$$
\half\uex''(t_n)\Delta t - \frac{1}{6}\uex'''(t_n)\Delta t^2
+ \Oof{\Delta t^3} = C^n + R^n\tp$$
Choosing
$$ C^n = \half\uex''(t_n)\Delta t,$$
makes
$$ R^n = \frac{1}{6}\uex'''(t_n)\Delta t^2 + \Oof{\Delta t^3}\tp$$
$$ u' = -au,\quad\Rightarrow\quad u''=-au'=a^2u\tp$$
Result for \( u''=a^2u \): apply Forward Euler to a perturbed ODE,
$$
\begin{equation}
u' = -\hat au ,\quad \hat a = a(1 - {\half}a\Delta t),
\tag{31}
\end{equation}
$$
to make a second-order scheme!
Use the other alternative \( u''=-au' \):
$$ u'=-au - {\half}a\Delta t u'\quad\Rightarrow\quad
\left( 1 + {\half}a\Delta t\right) u' = -au\tp$$
Apply Forward Euler:
$$
\left( 1 + {\half}a\Delta t\right)\frac{u^{n+1}-u^n}{\Delta t}
= -au^n,$$
which after some algebra can be written as
$$ u^{n+1} = \frac{1 - {\half}a\Delta t}{1+{\half}a\Delta t}u^n\tp$$
This is a Crank-Nicolson scheme (of second order)!
$$ [D_t u = -a\overline{u}^t]^{n+\half},$$
Definition of the truncation error \( R \) and correction terms \( C \):
$$ [D_t \uex + a\overline{\uex}^{t} = C + R]^{n+\half}\tp$$
Must Taylor expand
$$
C^{n+\half} + R^{n+\half} =
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
+ \frac{a}{8}\uex''(t_{n+\half})\Delta t^2 + \Oof{\Delta t^4}\tp$$
Let \( C^{n+\half} \) cancel the \( \Delta t^2 \) terms:
$$ C^{n+\half} =
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
+ \frac{a}{8}\uex''(t_{n})\Delta t^2\tp$$
Result: solve the perturbed ODE by a Crank-Nicolson method,
$$ u' = -\hat a u,\quad \hat a = a(1 - \frac{1}{12}a^2\Delta t^2)\tp$$
and experience an error \( \Oof{\Delta t^4} \).
$$ u'(t) = -a(t)u(t) + b(t)$$
Forward Euler:
$$
\begin{equation}
[D_t^+ u = -au + b]^n
\tp
\end{equation}
$$
The truncation error is found from
$$
\begin{equation}
[D_t^+ \uex + a\uex - b = R]^n
\tp
\end{equation}
$$
$$ \uex'(t_n) - \half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
+ a(t_n)\uex(t_n) - b(t_n) = R^n
\tp
$$
Because of the ODE, \( \uex'(t_n) + a(t_n)\uex(t_n) - b(t_n) =0 \), and
$$
\begin{equation}
R^n = -\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{32}
\tp
\end{equation}
$$
No problems with variable coefficients!
How does the truncation error depend on \( \uex \) in finite differences?
Consequence:
Problem: harmonic and geometric mean (error depends on \( \uex' \) and \( \uex \))
$$
\begin{equation}
u'=f(u,t)
\tag{33}
\end{equation}
$$
Crank-Nicolson scheme:
$$
\begin{equation}
[D_t u'=\overline{f}^{t}]^{n+\half}\tp
\tag{33}
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_t \uex' - \overline{f}^{t}= R]^{n+\half}\tp
\tag{35}
\end{equation}
$$
Using (19)-(20) for the arithmetic mean:
$$
\begin{align*}
\lbrack\overline{f}^{t}\rbrack^{n+\half} &=
\half(f(\uex^n,t_n) + f(\uex^{n+1},t_{n+1}))\\
&= f(\uex^{n+\half},t_{n+\half}) +
\frac{1}{8}\uex''(t_{n+\half})\Delta t^2
+ \Oof{\Delta t^4}\tp
\end{align*}
$$
With (3)-(4), (35) leads to \( R^{n+\half} \) equal to
$$
\uex'(t_{n+\half}) +
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
- f(\uex^{n+\half},t_{n+\half}) -
\frac{1}{8}\uex''(t_{n+\half})\Delta t^2
+ \Oof{\Delta t^4} \tp
$$
Since \( \uex'(t_{n+\half}) - f(\uex^{n+\half},t_{n+\half})=0 \),
the truncation error becomes
$$ R^{n+\half} = (\frac{1}{24}\uex'''(t_{n+\half})
- \frac{1}{8}\uex''(t_{n+\half})) \Delta t^2\tp
$$
The computational techniques worked well
even for this nonlinear ODE!
$$
\begin{equation}
u''(t) + \omega^2 u(t) = 0,\quad u(0)=I,\ u'(0)=0\tp
\tag{36}
\end{equation}
$$
Centered difference approximation:
$$
\begin{equation}
[D_tD_t u + \omega^2u=0]^n
\tag{37}
\tp
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_tD_t \uex + \omega^2\uex =R]^n
\tp
\end{equation}
$$
Use (15)-(16) to expand \( [D_t D_t\uex]^n \):
$$ [D_tD_t \uex]^n = \uex''(t_n) + \frac{1}{12}\uex''''(t_n)\Delta t^2,$$
Collect terms: \( \uex''(t) + \omega^2\uex(t)=0 \). Then,
$$
\begin{equation}
R^n = \frac{1}{12}\uex''''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tp
\end{equation}
$$
$$ [D_tD_t \uex + \omega^2\uex =C + R]^n,$$
$$ C^n = \frac{1}{12}\uex''''(t_n)\Delta t^2\tp$$
$$ [D_tD_t u + \omega^2(1 - \frac{1}{12}\omega^2\Delta t^2)u=0]^n,$$
Linear damping \( \beta u' \), nonlinear spring force \( s(u) \), and excitation \( F \):
$$
\begin{equation}
mu'' + \beta u' + s(u) =F(t)\tp
\tag{38}
\end{equation}
$$
Central difference discretization:
$$
\begin{equation}
[mD_tD_t u + \beta D_{2t} u + s(u)=F]^n
\tp
\end{equation}
$$
Truncation error is defined by
$$
\begin{equation}
[mD_tD_t \uex + \beta D_{2t} \uex + s(\uex)=F + R]^n
\tp
\end{equation}
$$
Using (15)-(16) and (5)-(6) we get
$$
\begin{align*}
\lbrack mD_tD_t \uex + \beta D_{2t} \uex\rbrack^n &=
m\uex''(t_n) + \beta\uex'(t_n) + \\
&\quad \left(\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{6}\uex'''(t_n)\right)\Delta t^2 + \Oof{\Delta t^4}
\end{align*}
$$
The terms
$$ m\uex''(t_n) + \beta\uex'(t_n) + \omega^2\uex(t_n) + s(\uex(t_n)) - F^n,$$
correspond to the ODE (= zero).
Result: accuracy of \( \Oof{\Delta t^2} \) since
$$
\begin{equation}
R^n = \left(\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{6}\uex'''(t_n)\right)\Delta t^2 + \Oof{\Delta t^4},
\tag{39}
\end{equation}
$$
Correction terms: complicated when the ODE has many terms...
$$
\begin{equation}
mu'' + \beta |u'|u' + s(u) =F(t)\tp
\tag{40}
\end{equation}
$$
Centered scheme: \( |u'|u' \) gives rise to a nonlinearity.
Linearization trick: use a geometric mean,
$$ [|u'|u']^n \approx |[u']^{n-\half}|[u']^{n+\half}\tp$$
Scheme:
$$
\begin{equation}
[mD_t D_t u]^n + \beta |[D_{t} u]^{n-\half}|[D_t u]^{n+\half}
+ s(u^n)=F^n\tp
\end{equation}
$$
Definition of \( R^n \):
$$
\begin{equation}
[mD_t D_t \uex]^n +
\beta |[D_{t} \uex]^{n-\half}|[D_t \uex]^{n+\half}
+ s(\uex^n)-F^n = R^n\tp
\end{equation}
$$
Truncation error of the geometric mean, see (21)-(22),
$$
\begin{align*}
|[D_{t} \uex]^{n-\half}|[D_t \uex]^{n+\half}
&= [|D_t\uex|D_t\uex]^n
- \frac{1}{4}u'(t_n)^2\Delta t^2 + \\
&\quad \frac{1}{4}u(t_n)u''(t_n)\Delta t^2
+ \Oof{\Delta t^4}\tp
\end{align*}
$$
Using (3)-(4) for the \( D_t\uex \) factors results in
$$
\begin{align*}
[|D_t\uex|D_t\uex]^n &= |\uex' + \frac{1}{24}\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4}|\times\\
&\quad (\uex' + \frac{1}{24}\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4})
\end{align*}
$$
For simplicity, remove the absolute value. The product becomes
$$
[D_t\uex D_t\uex]^n = (\uex'(t_n))^2 +
\frac{1}{12}\uex(t_n)\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4}\tp$$
With
$$ m[D_t D_t\uex]^n = m\uex''(t_n) + \frac{m}{12}\uex''''(t_n)\Delta t^2
+\Oof{\Delta t^4},$$
and using \( mu'' + \beta (u')^2 + s(u)=F \), we end up with
$$ R^n = (\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{12}\uex(t_n)\uex'''(t_n))
\Delta t^2 + \Oof{\Delta t^4}\tp$$
Second-order accuracy! Thanks to
$$
\begin{equation}
mu'' + \beta |u'|u' + s(u) =F(t)\tp
\tag{40}
\end{equation}
$$
Rewritten as first-order system:
$$
\begin{align}
u' &= v,
\tag{42} \\
v' &= \frac{1}{m}\left( F(t) - \beta |v|v - s(u)\right)\tp
\tag{43}
\end{align}
$$
To solution methods:
Forward step for \( u \), backward step for \( v \):
$$
\begin{align}
[D_t^+ u &= v]^n,
\tag{44} \\
[D_t^-v &= \frac{1}{m}( F(t) - \beta |v|v - s(u))]^{n+1}\tp
\tag{45}
\end{align}
$$
$$
\begin{align}
[D_t^+ u &= v]^n,
\tag{46} \\
[D_t^-v]^{n+1} &= \frac{1}{m}( F(t_{n+1}) - \beta |v^n|v^{n+1} - s(u^{n+1}))\tp
\tag{47}
\end{align}
$$
Staggered mesh:
Centered differences in (42)-(42):
$$
\begin{align}
[D_t u &= v]^{n-\half},
\tag{48} \\
[D_t v &= \frac{1}{m}( F(t) - \beta |v|v - s(u))]^{n}\tp
\tag{49}
\end{align}
$$
$$ |v^n|v^n \approx |v^{n-\half}|v^{n+\half}\tp$$
Resulting scheme:
$$
\begin{align}
[D_t u]^{n-\half} &= v^{n-\half},
\tag{50} \\
[D_t v]^n &= \frac{1}{m}( F(t_n) -
\beta |v^{n-\half}|v^{n+\half} - s(u^n))\tp
\tag{51}
\end{align}
$$
The truncation error in each equation is found from
$$
\begin{align*}
[D_t \uex]^{n-\half} &= \vex(t_{n-\half}) + R_u^{n-\half},\\
[D_t \vex]^n &= \frac{1}{m}( F(t_n) -
\beta |\vex(t_{n-\half})|\vex(t_{n+\half}) - s(u^n)) + R_v^n\tp
\end{align*}
$$
Using (3)-(4) for derivatives and (21)-(22)
for the geometric mean:
$$
\uex'(t_{n-\half}) +
\frac{1}{24}\uex'''(t_{n-\half})\Delta t^2 + \Oof{\Delta t^4}
= \vex(t_{n-\half}) + R_u^{n-\half},$$
and
$$
\vex'(t_n) =
\frac{1}{m}( F(t_n) -
\beta |\vex(t_n)|\vex(t_n) + \Oof{\Delta t^2} - s(u^n)) + R_v^n\tp
$$
Resulting truncation error is \( \Oof{\Delta t^2} \):
$$ R_u^{n-\half}= \Oof{\Delta t^2}, \quad R_v^n = \Oof{\Delta t^2}\tp$$
Comparing The schemes (50)-(51) and (46)-(47) are equivalent. Therefore, the forward/backward scheme with ad hoc linearization is also \( \Oof{\Delta t^2} \)!