Numerical investigations

Experiments with Schemes for Exponential Decay

Hans Petter Langtangen
Simula Research Laboratory
University of Oslo

August 20, 2012

Summary. This report investigates the accuracy of three finite difference schemes for the ordinary differential equation u'=-au with the aid of numerical experiments. Numerical artifacts are in particular demonstrated.

Mathematical problem

We address the initial-value problem u'(t)=-au(t), for t in (0,T], and with initial condition u(0)=I. Here, I, a, and T are prescribed parameters, and u(t) is the unknown function to be estimated. This mathematical model is relevant for physical phenomena featuring exponential decay in time, e.g., vertical pressure variation in the atmosphere, cooling of an object, and radioactive decay.

Numerical solution method

We use a mesh in time with equally spaced points. The theta-rule [1] is used to discretize the differential equation. This scheme corresponds to

Implementation

The numerical method is implemented in a Python function [2]: 
def solver(I, a, T, dt, theta):
    """Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
    Nt = int(round(T/float(dt)))  # no of intervals
    u = zeros(Nt+1)
    t = linspace(0, T, Nt+1)

    u[0] = I
    for n in range(0, Nt):
        u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
    return u, t

Numerical experiments

We define a set of numerical experiments where I, a, and T are fixed, while the time step and theta are varied. In particular, I=1, a=2, dt=1.25, 0.75, 0.5, 0.1.

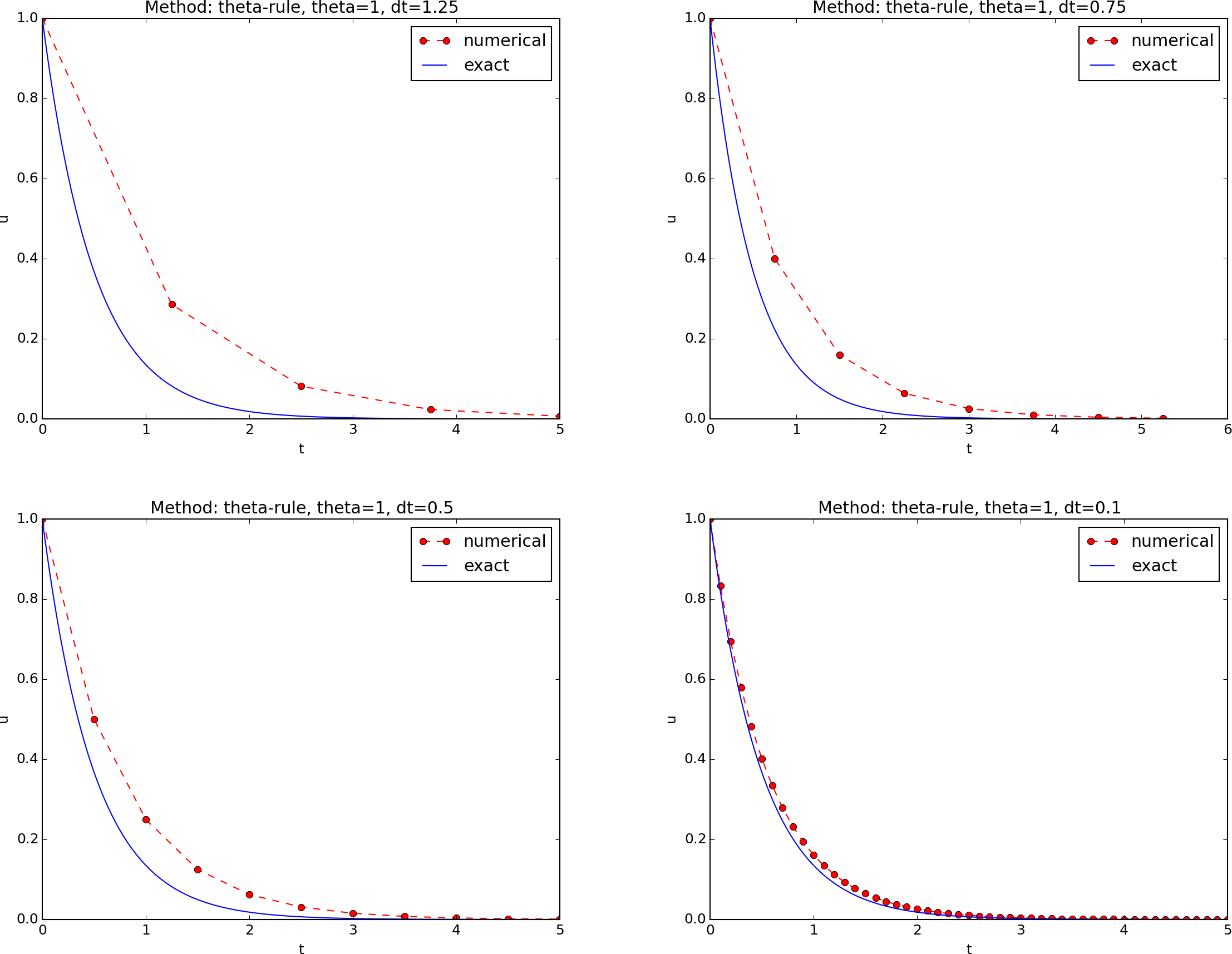
The Backward Euler method

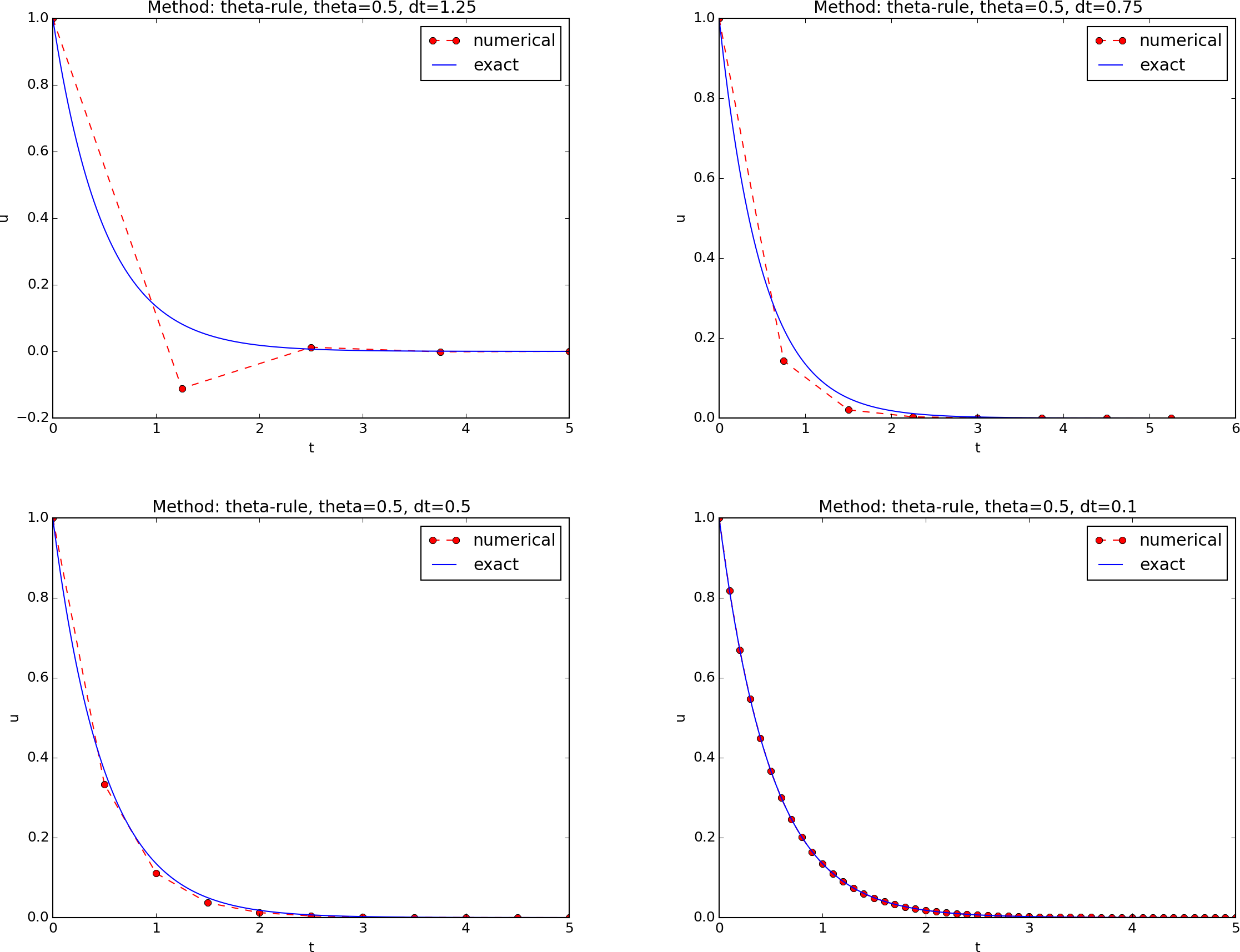
The Crank-Nicolson method

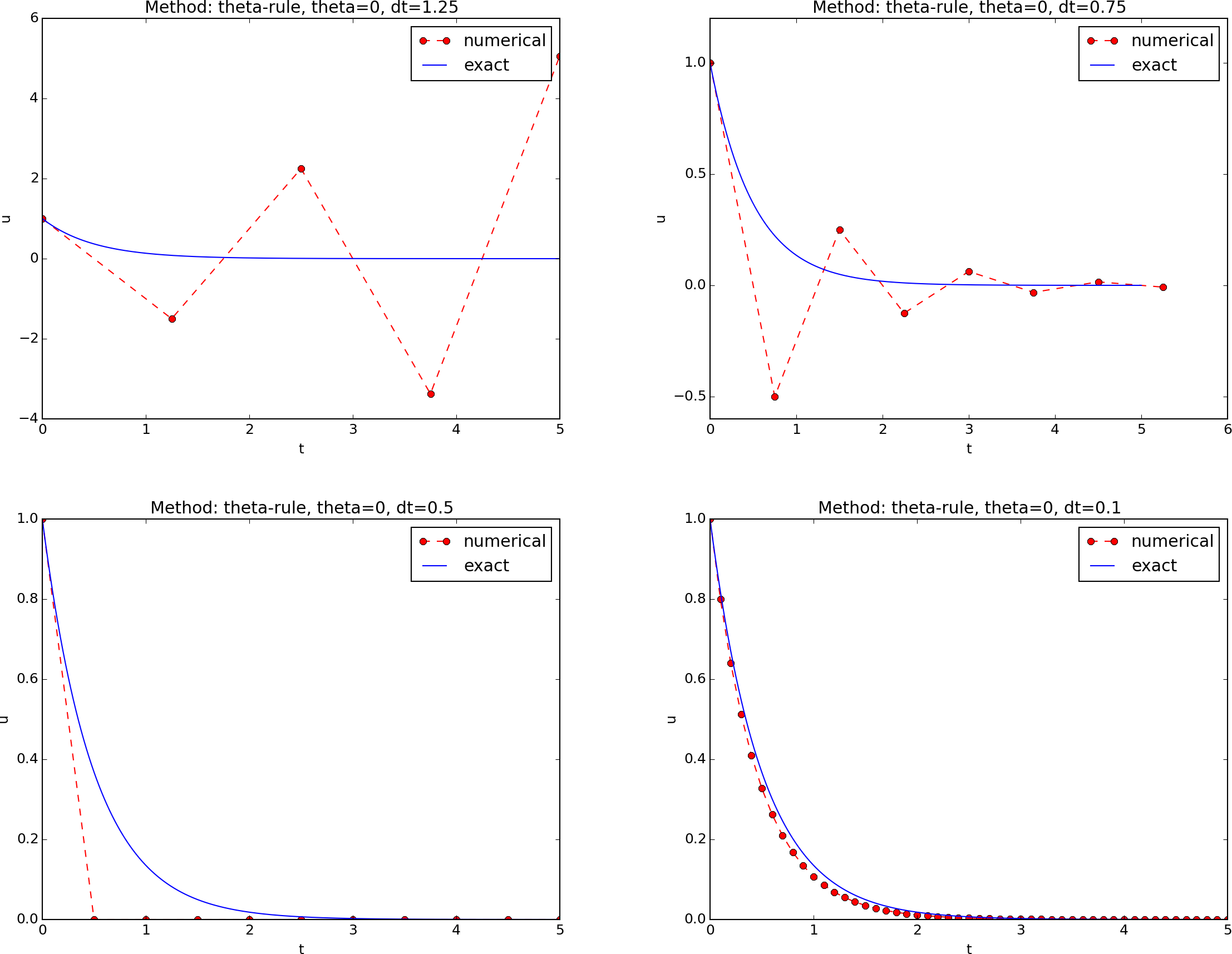
The Forward Euler method

Error versus time discretization

How E varies with the time step, for the three discretization methods, is shown below.

Observe: The data points for the three largest time steps in the Forward Euler method are not relevant as the solution behaves non-physically.

Summary

  1. For the Backward Euler scheme, we have first-order convergence.
  2. For the Crank-Nicolson scheme, we have second-order convergence.
  3. The Backward Euler scheme is always stable and gives qualitatively corrects results.
  4. The Crank-Nicolson scheme never blows up, but may give oscillating solutions if the time step is not sufficiently small.
  5. The Forward Euler scheme suffers from fast-growing solution if time time step is not small enough, but even below this limit one can have oscillating solutions (unless the time step is sufficiently small).

Bibliography

  1. A. Iserles. A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, 2009.
  2. H. P. Langtangen. A Primer on Scientific Programming With Python, Springer, 2012.