Copyright 2016, Hans Petter Langtangen. Released under CC Attribution 4.0 license
*Summary.* This report investigates the accuracy of three finite difference
schemes for the ordinary differential equation $u'=-au$ with the
aid of numerical experiments. Numerical artifacts are in particular
demonstrated.
<!--
Table of contents: Run pandoc with --toc option -->
<!-- !split -->
## Mathematical problem
<div id="math:problem"></div>
We address the initial-value problem
$$
\begin{align}
u'(t) &= -au(t), \quad t \in (0,T], \label{ode}\\
u(0) &= I, \label{initial:value}
\end{align}
$$
where $a$, $I$, and $T$ are prescribed parameters, and $u(t)$ is
the unknown function to be estimated. This mathematical model
is relevant for physical phenomena featuring exponential decay
in time, e.g., vertical pressure variation in the atmosphere,
cooling of an object, and radioactive decay.
## Numerical solution method
<div id="numerical:problem"></div>
We introduce a mesh in time with points $0 = t_0 < t_1 \cdots < t_{N_t}=T$.
For simplicity, we assume constant spacing $\Delta t$ between the
mesh points: $\Delta t = t_{n}-t_{n-1}$, $n=1,\ldots,N_t$. Let
$u^n$ be the numerical approximation to the exact solution at $t_n$.
The $\theta$-rule [@Iserles_2009]
is used to solve EQREF{ode} numerically:
$$
u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n,
$$
for $n=0,1,\ldots,N_t-1$. This scheme corresponds to
* The [Forward Euler](http://en.wikipedia.org/wiki/Forward_Euler_method)
scheme when $\theta=0$
* The [Backward Euler](http://en.wikipedia.org/wiki/Backward_Euler_method)
scheme when $\theta=1$
* The [Crank-Nicolson](http://en.wikipedia.org/wiki/Crank-Nicolson)
scheme when $\theta=1/2$
## Implementation
The numerical method is implemented in a Python function
[@Langtangen_2014] `solver` (found in the [`model.py`](http://bit.ly/29ayDx3) Python module file):
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~{.Python}
def solver(I, a, T, dt, theta):
"""Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
return u, t
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
## Numerical experiments
A set of numerical experiments has been carried out,
where $I$, $a$, and $T$ are fixed, while $\Delta t$ and
$\theta$ are varied. In particular, $I=1$, $a=2$,
$\Delta t = 1.25, 0.75, 0.5, 0.1$.
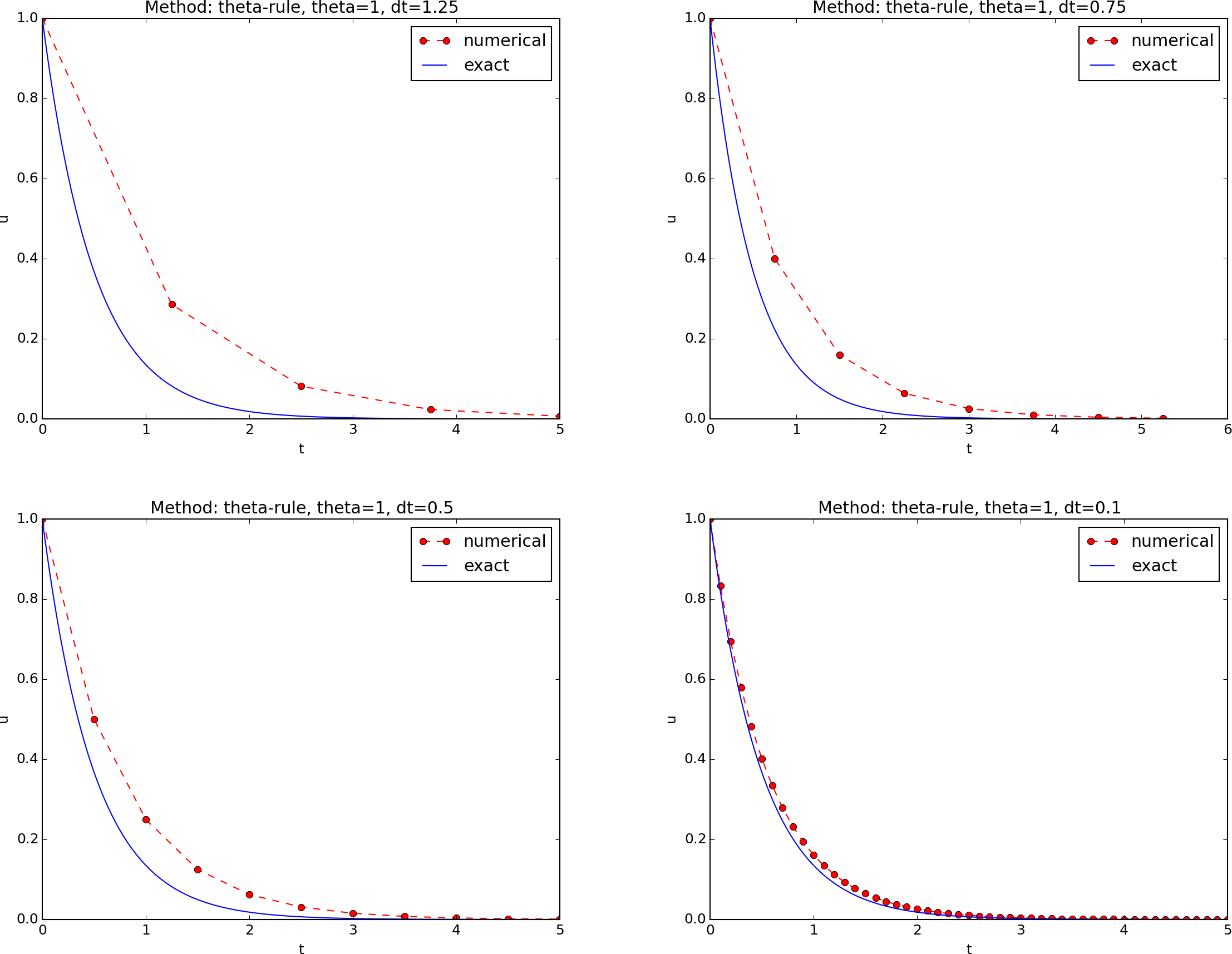
[Figure](#fig:BE) contains four plots, corresponding to
four decreasing $\Delta t$ values. The red dashed line
represent the numerical solution computed by the Backward
Euler scheme, while the blue line is the exact solution.
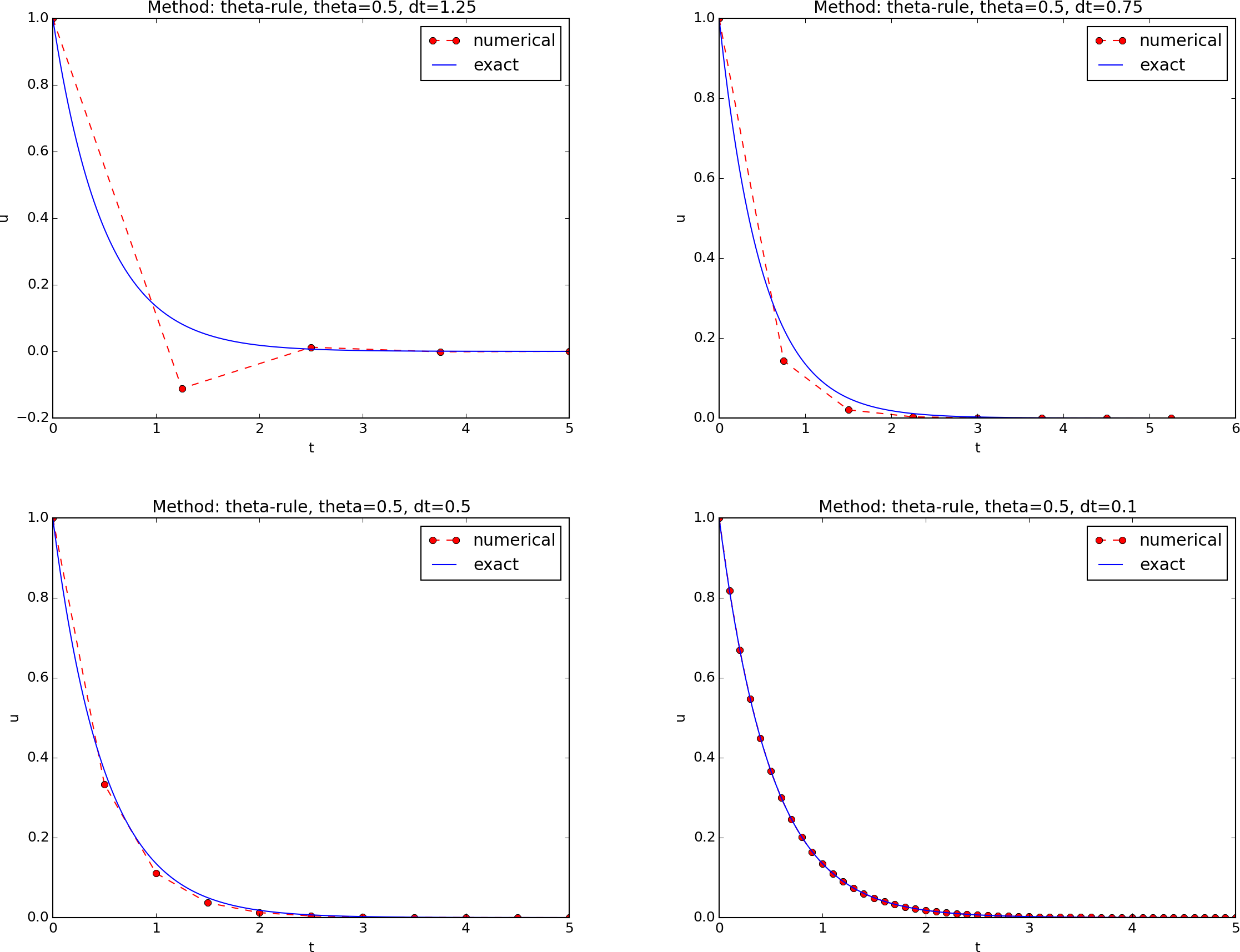
The corresponding results for the Crank-Nicolson and
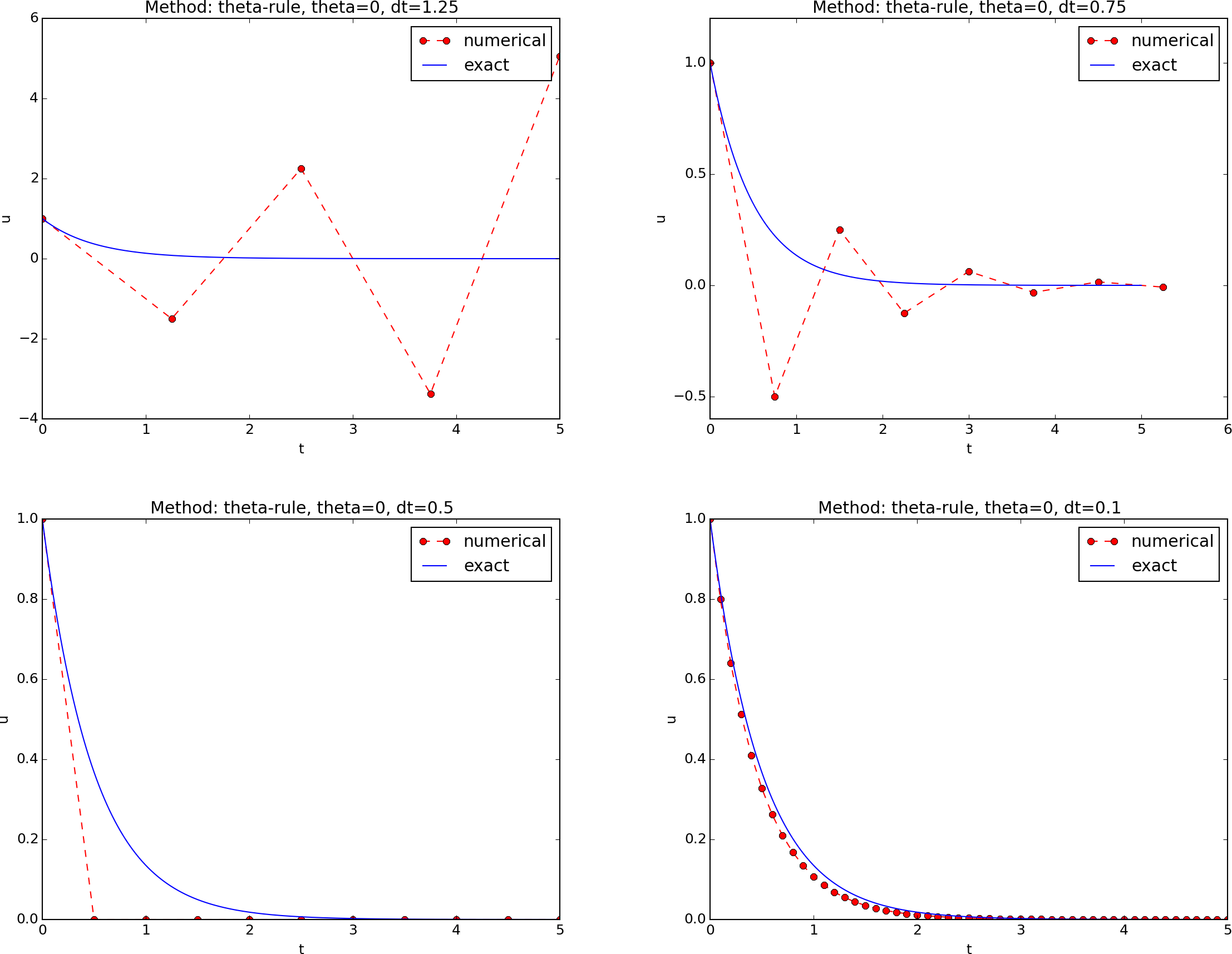
Forward Euler methods appear in Figures ref{fig:CN}
and ref{fig:FE}.
<!-- <img src="BE.png" width=800><p><em>The Backward Euler method for decreasing time step values. <div id="fig:BE"></div></em></p> -->
<!-- <img src="CN.png" width=800><p><em>The Crank-Nicolson method for decreasing time step values. <div id="fig:CN"></div></em></p> -->
<!-- <img src="FE.png" width=800><p><em>The Forward Euler method for decreasing time step values. <div id="fig:FE"></div></em></p> -->
## Error vs $\Delta t$
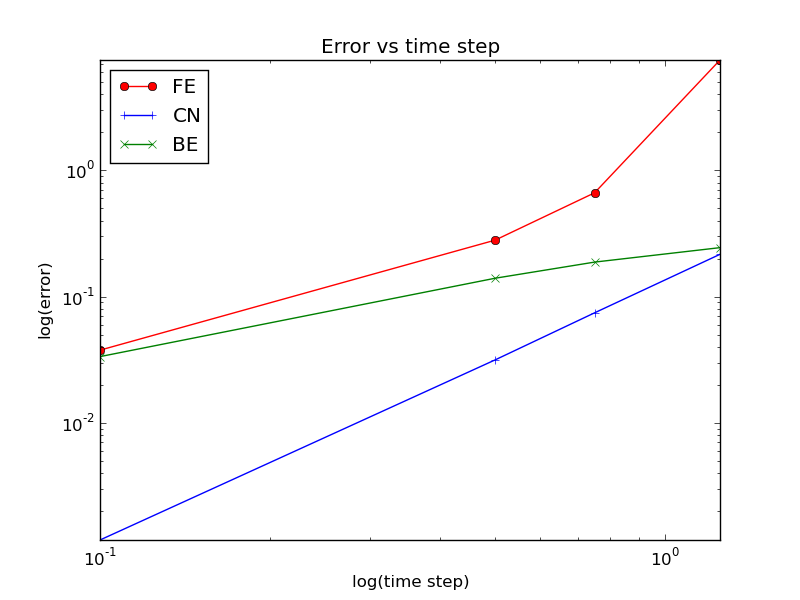
How the error
$$
E^n = \left(\int_0^T (Ie^{-at} - u^n)^2dt\right)^{\frac{1}{2}}
$$
varies with $\Delta t$ for the three numerical methods
is shown in [Figure](#fig:error).
*Observe:*
The data points for the three largest $\Delta t$ values in the
Forward Euler method are not relevant as the solution behaves
non-physically.
<!-- <img src="error.png" width=400><p><em>Variation of the error with the time step. <div id="fig:error"></div></em></p> -->
The $E$ numbers corresponding to [Figure](#fig:error)
are given in the table below.
$\Delta t$ $\theta=0$ $\theta=0.5$ $\theta=1$
---------- ---------- ------------ ----------
1.25 7.4630 0.2161 0.2440
0.75 0.6632 0.0744 0.1875
0.50 0.2797 0.0315 0.1397
0.10 0.0377 0.0012 0.0335
*Summary.*
1. $\theta =1$: $E\sim \Delta t$ (first-order convergence).
2. $\theta =0.5$: $E\sim \Delta t^2$ (second-order convergence).
3. $\theta =1$ is always stable and gives qualitatively corrects results.
4. $\theta =0.5$ never blows up, but may give oscillating solutions
if $\Delta t$ is not sufficiently small.
5. $\theta =0$ suffers from fast-growing solution if $\Delta t$ is
not small enough, but even below this limit one can have oscillating
solutions (unless $\Delta t$ is sufficiently small).
## Bibliography
1. <div id="Iserles_2009"></div> **A. Iserles**.
*A First Course in the Numerical Analysis of Differential Equations*,
second edition,
Cambridge University Press,
2009.
2. <div id="Langtangen_2014"></div> **H. P. Langtangen**.
*A Primer on Scientific Programming With Python*,
fifth edition,
Springer,
2016.