Ch.5: Array computing and curve plotting

Hans Petter Langtangen [1, 2]

 

[1] Simula Research Laboratory
[2] University of Oslo, Dept. of Informatics

 

Aug 21, 2016


Goal: learn to visualize functions





We need to learn about a new object: array

  • Curves \( y=f(x) \) are visualized by drawing straight lines between points along the curve

  • Meed to store the coordinates of the points along the curve in lists or arrays x and y

  • Arrays \( \approx \) lists, but computationally much more efficient

  • To compute the y coordinates (in an array) we need to learn about array computations or vectorization

  • Array computations are useful for much more than plotting curves!

The minimal need-to-know about vectors

  • Vectors are known from high school mathematics, e.g.,
    point \( (x,y) \) in the plane, point \( (x,y,z) \) in space

  • In general, a vector \( v \) is an \( n \)-tuple of numbers:
    \( v=(v_0,\ldots,v_{n-1}) \)

  • Vectors can be represented by lists: \( v_i \) is stored as v[i],
    but we shall use arrays instead

Vectors and arrays are key concepts in this chapter. It takes separate math courses to understand what vectors and arrays really are, but in this course we only need a small subset of the complete story. A learning strategy may be to just start using vectors/arrays in programs and later, if necessary, go back to the more mathematical details in the first part of Ch. 5.

The minimal need-to-know about arrays

Arrays are a generalization of vectors where we can have multiple indices: \( A_{i,j} \), \( A_{i,j,k} \)

Example: table of numbers, one index for the row, one for the column

 
$$ \left\lbrack\begin{array}{cccc} 0 & 12 & -1 & 5\\ -1 & -1 & -1 & 0\\ 11 & 5 & 5 & -2 \end{array}\right\rbrack \hspace{1cm} A = \left\lbrack\begin{array}{ccc} A_{0,0} & \cdots & A_{0,n-1}\\ \vdots & \ddots & \vdots\\ A_{m-1,0} & \cdots & A_{m-1,n-1} \end{array}\right\rbrack $$

 

  • The no of indices in an array is the rank or number of dimensions

  • Vector = one-dimensional array, or rank 1 array

  • In Python code, we use Numerical Python arrays instead of nested lists to represent mathematical arrays (because this is computationally more efficient)

Storing (x,y) points on a curve in lists

Collect points on a function curve \( y=f(x) \) in lists: 

>>> def f(x):
...     return x**3
...
>>> n = 5                 # no of points
>>> dx = 1.0/(n-1)        # x spacing in [0,1]
>>> xlist = [i*dx for i in range(n)]
>>> ylist = [f(x) for x in xlist]

>>> pairs = [[x, y] for x, y in zip(xlist, ylist)]

Turn lists into Numerical Python (NumPy) arrays: 

>>> import numpy as np        # module for arrays
>>> x = np.array(xlist)      # turn list xlist into array
>>> y = np.array(ylist)

Make arrays directly (instead of lists)

The pro drops lists and makes NumPy arrays directly: 

>>> n = 5                     # number of points
>>> x = np.linspace(0, 1, n) # n points in [0, 1]
>>> y = np.zeros(n)          # n zeros (float data type)
>>> for i in xrange(n):
...     y[i] = f(x[i])
...

Note:

  • xrange is like range but faster (esp. for large n - xrange does not explicitly build a list of integers, xrange just lets you loop over the values)

  • Entire arrays must be made by numpy (np) functions

Arrays are not as flexible as list, but computational much more efficient

  • List elements can be any Python objects

  • Array elements can only be of one object type

  • Arrays are very efficient to store in memory and compute with
    if the element type is float, int, or complex

  • Rule: use arrays for sequences of numbers!

We can work with entire arrays at once - instead of one element at a time

Compute the sine of an array: 

from math import sin

for i in xrange(len(x)):
    y[i] = sin(x[i])

However, if x is array, y can be computed by 

y = np.sin(x)                  # x: array, y: array

The loop is now inside np.sin and implemented in very efficient C code.

Operating on entire arrays at once is called vectorization

Vectorization gives:

  • shorter, more readable code, closer to the mathematics

  • much faster code

Use %timeit in IPython to measure the speed-up for \( y=\sin x e^{-x} \): 

In [1]: n = 100000

In [2]: import numpy as np

In [3]: x = np.linspace(0, 2*np.pi, n+1)

In [4]: y = np.zeros(len(x))

In [5]: %timeit for i in xrange(len(x)): \
        y[i] = np.sin(x[i])*np.exp(-x[i])
1 loops, best of 3: 247 ms per loop

In [6]: %timeit y = np.sin(x)*np.exp(-x)
100 loops, best of 3: 4.77 ms per loop

In [7]: 247/4.77
Out[7]: 51.781970649895186  # vectorization: 50x speed-up!

A function f(x) written for a number x usually works for array x too 

from numpy import sin, exp, linspace

def f(x):
    return x**3 + sin(x)*exp(-3*x)

x = 1.2                     # float object
y = f(x)                    # y is float

x = linspace(0, 3, 10001)   # 10000 intervals in [0,3]
y = f(x)                    # y is array

Note: math is for numbers and numpy for arrays. 

>>> import math, numpy
>>> x = numpy.linspace(0, 1, 11)
>>> math.sin(x[3])
0.2955202066613396
>>> math.sin(x)
...
TypeError: only length-1 arrays can be converted to Python scalars
>>> numpy.sin(x)
array([ 0.     ,  0.09983,  0.19866,  0.29552,  0.38941,
        0.47942,  0.56464,  0.64421,  0.71735,  0.78332,
        0.84147])

Array arithmetics is broken down to a series of unary/binary array operations

  • Consider y = f(x), where f returns x**3 + sin(x)*exp(-3*x)

  • f(x) leads to the following set of vectorized sub-computations:

    1. r1 = x**3
      for i in range(len(x)): r1[i] = x[i]**3
      (but with loop in C)

    2. r2 = sin(x) (computed elementwise in C)

    3. r3 = -3*x

    4. r4 = exp(r3)

    5. r5 = r3*r4

    6. r6 = r1 + r5

    7. y = r6

  • Note: this is the same set of operations as you would do with a calculator when x is a number

Very important application: vectorized code for computing points along a curve

 
$$ f(x) = x^2e^{-\frac{1}{2}x}\sin(x-\frac{1}{3}\pi),\quad x\in [0, 4\pi]$$

 

Vectorized computation of \( n+1 \) points along the curve. 

from numpy import *

n = 100
x = linspace(0, 4*pi, n+1)
y = 2.5 + x**2*exp(-0.5*x)*sin(x-pi/3)

New term: vectorization

  • Scalar: a number

  • Vector or array: sequence of numbers (vector in mathematics)

  • We speak about scalar computations (one number at a time) versus vectorized computations (operations on entire arrays, no Python loops)

  • Vectorized functions can operate on arrays (vectors)

  • Vectorization is the process of turning a non-vectorized algorithm with (Python) loops into a vectorized version without (Python) loops

  • Mathematical functions in Python without if tests automatically work for both scalar and vector (array) arguments (i.e., no vectorization is needed by the programmer)

Plotting the curve of a function: the very basics

Plot the curve of \( y(t) = t^2e^{-t^2} \): 

from scitools.std import *  # import numpy and plotting

# Make points along the curve
t = linspace(0, 3, 51)      # 50 intervals in [0, 3]
y = t**2*exp(-t**2)         # vectorized expression

plot(t, y)           # make plot on the screen
savefig('fig.pdf')   # make PDF image for reports
savefig('fig.png')   # make PNG image for web pages





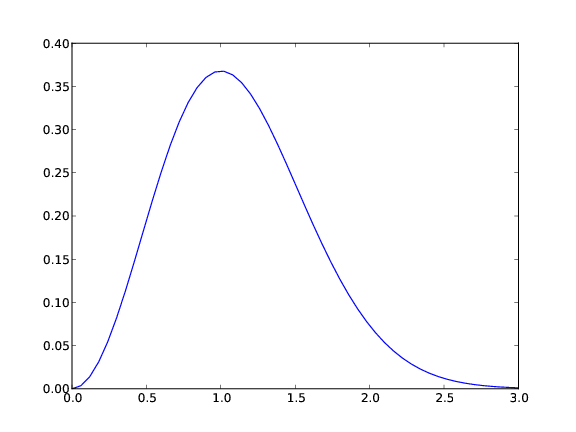
A plot should have labels on axis and a title





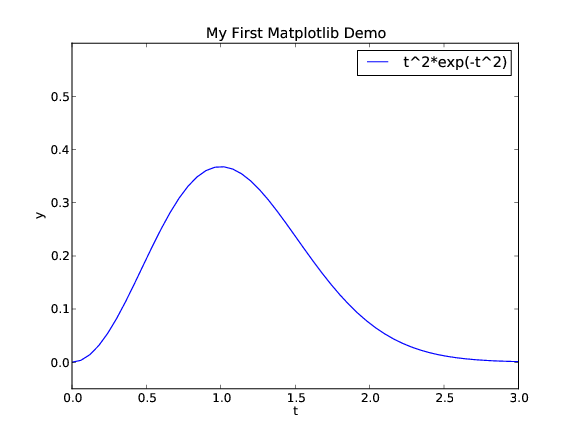
The code that makes the last plot 

from scitools.std import *  # import numpy and plotting

def f(t):
    return t**2*exp(-t**2)

t = linspace(0, 3, 51)    # t coordinates
y = f(t)                  # corresponding y values

plot(t, y)

xlabel('t')               # label on the x axis
ylabel('y')               # label on the y axix
legend('t^2*exp(-t^2)')   # mark the curve
axis([0, 3, -0.05, 0.6])  # [tmin, tmax, ymin, ymax]
title('My First Easyviz Demo')

SciTools vs. NumPy and Matplotlib

  • SciTools is a Python package with lots of useful tools for mathematical computations, developed here in Oslo (Langtangen, Ring, Wilbers, Bredesen, ...)

  • Easyviz is a subpackage of SciTools (scitools.easyviz) doing plotting with Matlab-like syntax

  • Easyviz can use many plotting engine to produce a plot: Matplotlib, Gnuplot, Grace, Matlab, VTK, OpenDx, ... but the syntax remains the same

  • Matplotlib is the standard plotting package in the Python community - Easyviz can use the same syntax as Matplotlib

from scitools.std import *

# is basically equivalent to

from numpy import *
from matplotlib.pyplot import *

Note: SciTools (by default) adds markers to the lines, Matplotlib does not

Easyviz (imported from scitools.std) allows a more compact "Pythonic" syntax for plotting curves

Use keyword arguments instead of separate function calls: 

plot(t, y,
     xlabel='t',
     ylabel='y',
     legend='t^2*exp(-t^2)',
     axis=[0, 3, -0.05, 0.6],
     title='My First Easyviz Demo',
     savefig='tmp1.png',
     show=True)   # display on the screen (default)

(This cannot be done with Matplotlib.)





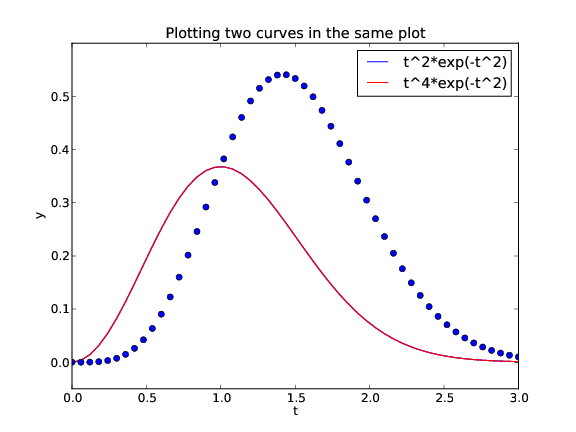
Plotting several curves in one plot

Plot \( t^2e^{-t^2} \) and \( t^4e^{-t^2} \) in the same plot: 

from scitools.std import *   # curve plotting + array computing

def f1(t):
    return t**2*exp(-t**2)

def f2(t):
    return t**2*f1(t)

t = linspace(0, 3, 51)
y1 = f1(t)
y2 = f2(t)

plot(t, y1)
hold('on')   # continue plotting in the same plot
plot(t, y2)

xlabel('t')
ylabel('y')
legend('t^2*exp(-t^2)', 't^4*exp(-t^2)')
title('Plotting two curves in the same plot')
savefig('tmp2.png')

Alternative, more compact plot command 

plot(t, y1, t, y2,
     xlabel='t', ylabel='y',
     legend=('t^2*exp(-t^2)', 't^4*exp(-t^2)'),
     title='Plotting two curves in the same plot',
     savefig='tmp2.pdf')

# equivalent to
plot(t, y1)
hold('on')
plot(t, y2)

xlabel('t')
ylabel('y')
legend('t^2*exp(-t^2)', 't^4*exp(-t^2)')
title('Plotting two curves in the same plot')
savefig('tmp2.pdf')

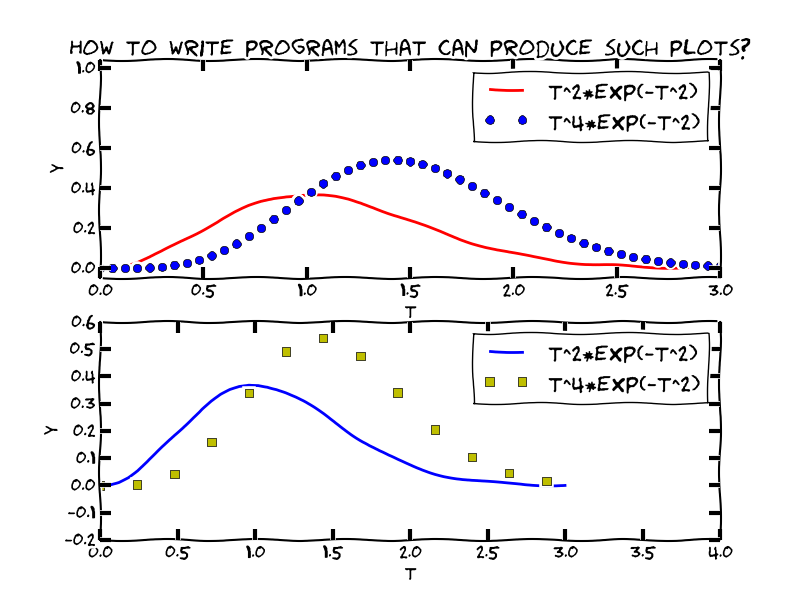
The resulting plot with two curves





Controlling line styles

When plotting multiple curves in the same plot, the different lines (normally) look different. We can control the line type and color, if desired: 

plot(t, y1, 'r-')   # red (r) line (-)
hold('on')
plot(t, y2, 'bo')   # blue (b) circles (o)

# or
plot(t, y1, 'r-', t, y2, 'bo')

Documentation of colors and line styles: see the book, Ch. 5, or 

Unix> pydoc scitools.easyviz

Quick plotting with minimal typing

A lazy pro would do this: 

t = linspace(0, 3, 51)
plot(t, t**2*exp(-t**2), t, t**4*exp(-t**2))

Plot function given on the command line

Task: plot function given on the command line. 

Terminal> python plotf.py expression xmin xmax
Terminal> python plotf.py "exp(-0.2*x)*sin(2*pi*x)" 0 4*pi

Should plot \( e^{-0.2x}\sin (2\pi x) \), \( x\in [0,4\pi] \). plotf.py should work for "any" mathematical expression.

Solution

Complete program: 

from scitools.std import *
# or alternatively
from numpy import *
from matplotlib.pyplot import *

formula = sys.argv[1]
xmin = eval(sys.argv[2])
xmax = eval(sys.argv[3])

x = linspace(xmin, xmax, 101)
y = eval(formula)
plot(x, y, title=formula)

Let's make a movie/animation





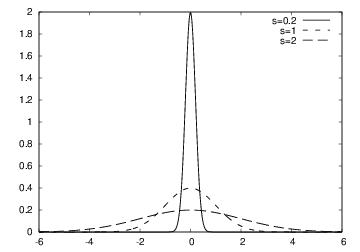
The Gaussian/bell function

 
$$ f(x; m, s) = {1\over\sqrt{2\pi}}{1\over s}\exp{\left[-{1\over2}\left({x-m\over s}\right)^2\right]} $$

 

  • \( m \) is the location of the peak

  • \( s \) is a measure of the width of the function

  • Make a movie (animation) of how \( f(x;m,s) \) changes shape as \( s \) goes from 2 to 0.2



Movies are made from a (large) set of individual plots

  • Goal: make a movie showing how \( f(x) \) varies in shape as \( s \) decreases

  • Idea: put many plots (for different \( s \) values) together
    (exactly as a cartoon movie)

  • How to program: loop over \( s \) values, call plot for each \( s \) and make hardcopy, combine all hardcopies to a movie

  • Very important: fix the \( y \) axis! Otherwise, the \( y \) axis always adapts to the peak of the function and the visual impression gets completely wrong

The complete code for making the animation 

from scitools.std import *
import time

def f(x, m, s):
    return (1.0/(sqrt(2*pi)*s))*exp(-0.5*((x-m)/s)**2)

m = 0;  s_start = 2;  s_stop = 0.2
s_values = linspace(s_start, s_stop, 30)

x = linspace(m -3*s_start, m + 3*s_start, 1000)
# f is max for x=m (smaller s gives larger max value)
max_f = f(m, m, s_stop)

# Show the movie on the screen
# and make hardcopies of frames simultaneously
import time
frame_counter = 0

for s in s_values:
    y = f(x, m, s)
    plot(x, y, axis=[x[0], x[-1], -0.1, max_f],
         xlabel='x', ylabel='f', legend='s=%4.2f' % s,
         savefig='tmp_%04d.png' % frame_counter)
    frame_counter += 1
    #time.sleep(0.2)  # pause to control movie speed

How to combine plot files to a movie (video file)

We now have a lot of files: 

tmp_0000.png  tmp_0001.png  tmp_0002.png ...

We use some program to combine these files to a video file:

  • convert for animted GIF format (if just a few plot files)

  • ffmpeg (or avconv) for MP4, WebM, Ogg, and Flash formats

Make and play animated GIF file

Tool: convert from the ImageMagick software suite.

Unix command: 

Terminal> convert -delay 50 tmp_*.png movie.gif

Delay: 50/100 s, i.e., 0.5 s between each frame.

Play animated GIF file with animate from ImageMagick: 

Terminal> animate movie.gif

or insert this HTML code in some file tmp.html loaded into a browser: 

<img src="movie.gif">

Making MP4, Ogg, WebM, or Flash videos

Tool: ffmpeg or avconv 

Terminal> ffmpeg -r 5 -i tmp_%04d.png -vcodec flv movie.flv

where

  • -r 5 specifies 5 frames per second

  • -i tmp_%04d.png specifies filenames
    (tmp_0000.png, tmp_0001.png, ...)

Different formats apply different codecs (-vcodec) and video filenamet extensions:


Format Codec and filename
Flash -vcodec flv movie.flv
MP4 -vcodec libx264 movie.mp4
Webm -vcodec libvpx movie.webm
Ogg -vcodec libtheora movie.ogg

How to play movie files in general (with vlc) 

Terminal> vlc movie.flv
Terminal> vlc movie.ogg
Terminal> vlc movie.webm
Terminal> vlc movie.mp4

Other players (on Linux) are mplayer, totem, ...

HTML PNG file player 

Terminal> scitools movie output_file=mymovie.html fps=4 tmp_*.png

makes a player of tmp_*.png files in a file mymovie.html (load into a web browser)

It is possible to plot curves in pure text (!)

  • Plots are stored in image files of type PDF and PNG

  • Sometimes you want a plot to be included in your program,
    e.g., to prove that the curve looks right in a compulsory exercise where only the program (and not a nicely typeset report) is submitted

  • scitools.aplotter can then be used for drawing primitive curves in pure text (ASCII) format

>>> from scitools.aplotter import plot
>>> from numpy import linspace, exp, cos, pi
>>> x = linspace(-2, 2, 81)
>>> y = exp(-0.5*x**2)*cos(pi*x)
>>> plot(x, y)

Try these statements out!

Let's try to plot a discontinuous function

The Heaviside function is frequently used in science and engineering:

 
$$ H(x) = \left\lbrace\begin{array}{ll} 0, & x < 0\\ 1, & x\geq 0 \end{array}\right. $$

 

Python implementation: 

def H(x):
    return (0 if x < 0 else 1)





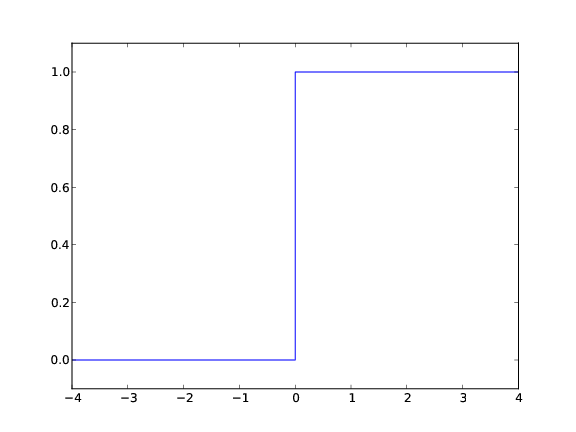
Plotting the Heaviside function: first try

Standard approach: 

x = linspace(-10, 10, 5)  # few points (simple curve)
y = H(x)
plot(x, y)

First problem: ValueError error in H(x) from if x < 0

Let us debug in an interactive shell: 

>>> x = linspace(-10,10,5)
>>> x
array([-10.,  -5.,   0.,   5.,  10.])
>>> b = x < 0
>>> b
array([ True,  True, False, False, False], dtype=bool)
>>> bool(b)  # evaluate b in a boolean context
...
ValueError: The truth value of an array with more than
one element is ambiguous. Use a.any() or a.all()

if x < 0 does not work if x is array

Remedy 1: use a loop over x values. 

def H_loop(x):
    r = zeros(len(x))  # or r = x.copy()
    for i in xrange(len(x)):
        r[i] = H(x[i])
    return r

n = 5
x = linspace(-5, 5, n+1)
y = H_loop(x)

Downside: much to write, slow code if n is large

if x < 0 does not work if x is array

Remedy 2: use vectorize. 

from numpy import vectorize

# Automatic vectorization of function H
Hv = vectorize(H)
# Hv(x) works with array x

Downside: The resulting function is as slow as Remedy 1

if x < 0 does not work if x is array

Remedy 3: code the if test differently. 

def Hv(x):
    return where(x < 0, 0.0, 1.0)

More generally: 

def f(x):
    if condition:
        x = <expression1>
    else:
        x = <expression2>
    return x

def f_vectorized(x):
def f_vectorized(x):
    x1 = <expression1>
    x2 = <expression2>
    r = np.where(condition, x1, x2)
    return r

Back to plotting the Heaviside function

With a vectorized Hv(x) function we can plot in the standard way 

x = linspace(-10, 10, 5)   # linspace(-10, 10, 50)
y = Hv(x)
plot(x, y, axis=[x[0], x[-1], -0.1, 1.1])





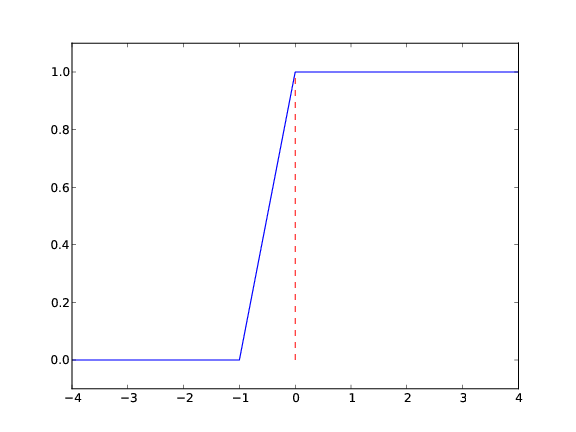
How to make the function look discontinuous in the plot?

  • Newbie: use a lot of \( x \) points; the curve gets steeper

  • Pro: plot just two horizontal line segments
    one from \( x=-10 \) to \( x=0 \), \( y=0 \); and one from \( x=0 \) to \( x=10 \), \( y=1 \)

plot([-10, 0, 0, 10], [0, 0, 1, 1],
     axis=[x[0], x[-1], -0.1, 1.1])

Draws straight lines between \( (-10,0) \), \( (0,0) \), \( (0,1) \), \( (10, 1) \)

The final plot of the discontinuous Heaviside function





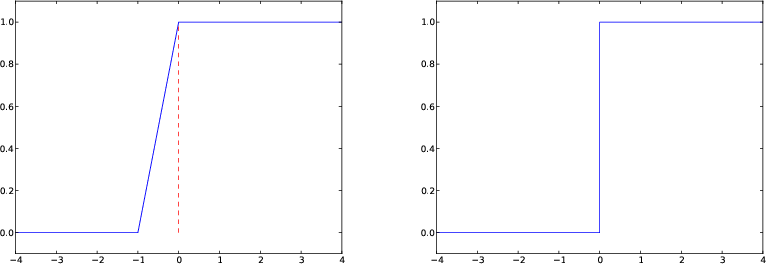
Removing the vertical jump from the plot

Question.

Some will argue and say that at high school they would draw \( H(x) \) as two horizontal lines without the vertical line at \( x=0 \), illustrating the jump. How can we plot such a curve?

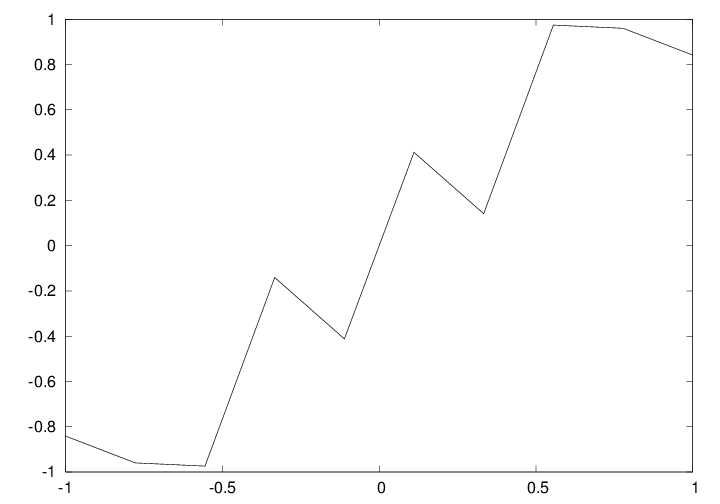
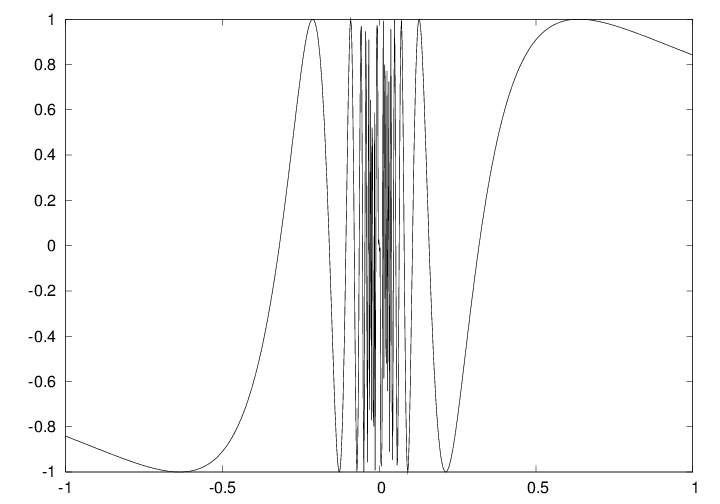
Some functions are challenging to visualize

Plot \( f(x) = \sin (1/x) \). 

def f(x):
    return sin(1.0/x)

x1 = linspace(-1, 1, 10)    # use 10 points
x2 = linspace(-1, 1, 1000)  # use 1000 points
plot(x1, f(x1), label='%d points' % len(x))
plot(x2, f(x2), label='%d points' % len(x))

Plot based on 10 points





Plot based on 1000 points





Assignment of an array does not copy the elements! 

a = x
a[-1] = 1000

Is x[-1] also changed to 1000?
Yes, because a refers to the same array as x.

Avoid changing x by letting a be a copy of x: 

a = x.copy()

The same yields slices: 

a = x[r:]      # a refers to a part of the x array
a[-1] = 1000   # changes x[-1]!
a = x[r:].copy()
a[-1] = 1000   # does not change x[-1]

In-place array arithmetics

The two following statements are mathematically equivalent: 

a = a + b    # a and b are arrays
a += b

However,

  • a = a + b is computed as (extra array needed)

    1. r1 = a + b

    2. a = r1

  • a += b is computed as a[i] += b[i] for i in all indices (i.e., not extra array)

  • a += b is an in-place addition, because we change each element in a, rather than letting the name a refer to a new array, the result of a+b

In-place array arithmetics can save memory demands

Consider 

a = (3*x**4 + 2*x + 4)/(x + 1)

Here are the actual computations in the computer: 

r1 = x**4;  r2 = 3*r1;  r3 = 2*x;  r4 = r1 + r3
r5 = r4 + 4;  r6 = x + 1; r7 = r5/r6; a = r7

With in-place arithmetics we can save four extra arrays, though at the cost of much less readable code: 

a = x.copy()
a **= 4
a *= 3
a += 2*x
a += 4
a /= x + 1

In-place arithmetics only saves memory, no significant speed-up

Let's use IPython to measure the computational time: 

In [1]: def expression(x):
   ...:     return (3*x**4 + 2*x + 4)/(x + 1)
   ...:

In [2]: def expression_inplace(x):
   ...:     a = x.copy()
   ...:     a **= 4
   ...:     a *= 3
   ...:     a += 2*x
   ...:     a += 4
   ...:     a /= x + 1
   ...:     return a
   ...:

In [3]: import numpy as np

In [4]: x = np.linspace(0, 1, 10000000)

In [5]: %timeit  expression(x)
1 loops, best of 3: 771 ms per loop

In [6]: %timeit  expression_inplace(x)
1 loops, best of 3: 728 ms per loop

Only 5% speed-up, so use +=, -=, etc. when arrays are large and you need to save memory

Useful array operations

Make a new array with same size as another array: 

from numpy import *

# x is numpy array
a = x.copy()

# or
a = zeros(x.shape, x.dtype)

# or
a = zeros_like(x)  # zeros and same size as x

Make sure a list or array is an array: 

a = asarray(a)
b = asarray(somearray, dtype=float)  # specify data type

Test if an object is an array: 

>>> type(a)
<type 'numpy.ndarray'>
>>> isinstance(a, ndarray)
True

Example: vectorizing a constant function 

def f(x):
    return 2

Vectorized version must return array of 2's: 

def fv(x):
    return zeros(x.shape, x.dtype) + 2

New version valid both for scalar and array x: 

def f(x):
    if isinstance(x, (float, int)):
        return 2
    elif isinstance(x, ndarray):
        return zeros(x.shape, x.dtype) + 2
    else:
        raise TypeError(
           'x must be int/float/ndarray, not %s' % type(x))

Generalized array indexing

Recall slicing: a[f:t:i], where the slice f:t:i implies a set of indices (from, to, increment).

Any integer list or array can be used to indicate a set of indices: 

>>> a = linspace(1, 8, 8)
>>> a
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.])
>>> a[[1,6,7]] = 10
>>> a
array([  1.,  10.,   3.,   4.,   5.,   6.,  10.,  10.])
>>> a[range(2,8,3)] = -2   # same as a[2:8:3] = -2
>>> a
array([  1.,  10.,  -2.,   4.,   5.,  -2.,  10.,  10.])

Generalized array indexing with boolean expressions 

>>> a < 0
[False, False, True, False, False, True, False, False]

>>> a[a < 0]           # pick out all negative elements
array([-2., -2.])

>>> a[a < 0] = a.max() # if a[i]<10, set a[i]=10
>>> a
array([  1.,  10.,  10.,   4.,   5.,  10.,  10.,  10.])

Two-dimensional arrays; math intro

When we have a table of numbers,

 
$$ \left\lbrack\begin{array}{cccc} 0 & 12 & -1 & 5\\ -1 & -1 & -1 & 0\\ 11 & 5 & 5 & -2 \end{array}\right\rbrack $$

 
(called matrix by mathematicians) it is natural to use a two-dimensional array \( A_{i,j} \) with one index for the rows and one for the columns:

 
$$ A = \left\lbrack\begin{array}{ccc} A_{0,0} & \cdots & A_{0,n-1}\\ \vdots & \ddots & \vdots\\ A_{m-1,0} & \cdots & A_{m-1,n-1} \end{array}\right\rbrack $$

 

Two-dimensional arrays; Python code

Making and filling a two-dimensional NumPy array goes like this: 

A = zeros((3,4))   # 3x4 table of numbers
A[0,0] = -1
A[1,0] =  1
A[2,0] = 10
A[0,1] = -5
...
A[2,3] = -100

# can also write (as for nested lists)
A[2][3] = -100

From nested list to two-dimensional array

Let us make a table of numbers in a nested list: 

>>> Cdegrees = [-30 + i*10 for i in range(3)]
>>> Fdegrees = [9./5*C + 32 for C in Cdegrees]
>>> table = [[C, F] for C, F in zip(Cdegrees, Fdegrees)]
>>> print table
[[-30, -22.0], [-20, -4.0], [-10, 14.0]]

Turn into NumPy array: 

>>> table2 = array(table)
>>> print table2
[[-30. -22.]
 [-20.  -4.]
 [-10.  14.]]

How to loop over two-dimensional arrays 

>>> table2.shape   # see the number of elements in each dir.
(3, 2)             # 3 rows, 2 columns

A for loop over all array elements: 

>>> for i in range(table2.shape[0]):
...     for j in range(table2.shape[1]):
...         print 'table2[%d,%d] = %g' % (i, j, table2[i,j])
...
table2[0,0] = -30
table2[0,1] = -22
...
table2[2,1] = 14

Alternative single loop over all elements: 

>>> for index_tuple, value in np.ndenumerate(table2):
...     print 'index %s has value %g' % \
...           (index_tuple, table2[index_tuple])
...
index (0,0) has value -30
index (0,1) has value -22
...
index (2,1) has value 14
>>> type(index_tuple)
<type 'tuple'>

How to take slices of two-dimensional arrays

Rule: can use slices start:stop:inc for each index 

table2[0:table2.shape[0], 1]  # 2nd column (index 1)
array([-22.,  -4.,  14.])

>>> table2[0:, 1]             # same
array([-22.,  -4.,  14.])

>>> table2[:, 1]              # same
array([-22.,  -4.,  14.])

>>> t = linspace(1, 30, 30).reshape(5, 6)
>>> t[1:-1:2, 2:]
array([[  9.,  10.,  11.,  12.],
       [ 21.,  22.,  23.,  24.]])
>>> t
array([[  1.,   2.,   3.,   4.,   5.,   6.],
       [  7.,   8.,   9.,  10.,  11.,  12.],
       [ 13.,  14.,  15.,  16.,  17.,  18.],
       [ 19.,  20.,  21.,  22.,  23.,  24.],
       [ 25.,  26.,  27.,  28.,  29.,  30.]])

Time for a question

Problem:

Given 

>>> t
array([[  1.,   2.,   3.,   4.,   5.,   6.],
       [  7.,   8.,   9.,  10.,  11.,  12.],
       [ 13.,  14.,  15.,  16.,  17.,  18.],
       [ 19.,  20.,  21.,  22.,  23.,  24.],
       [ 25.,  26.,  27.,  28.,  29.,  30.]])

What will t[1:-1:2, 2:] be?

Solution:

Slice 1:-1:2 for first index results in 

[  7.,   8.,   9.,  10.,  11.,  12.]
[ 19.,  20.,  21.,  22.,  23.,  24.]

Slice 2: for the second index then gives 

[  9.,  10.,  11.,  12.]
[ 21.,  22.,  23.,  24.]

Summary of vectors and arrays

  • Vector/array computing: apply a mathematical expression to every element in the vector/array (no loops in Python)

  • Ex: sin(x**4)*exp(-x**2), x can be array or scalar
    for array the i'th element becomes sin(x[i]**4)*exp(-x[i]**2)

  • Vectorization: make scalar mathematical computation valid for vectors/arrays

  • Pure mathematical expressions require no extra vectorization

  • Mathematical formulas involving if tests require manual work for vectorization:

scalar_result = expression1 if condition else expression2
vector_result = where(condition, expression1, expression2)

Summary of plotting \( y=f(x) \) curves

Curve plotting (unified syntax for Matplotlib and SciTools): 

from matplotlib.pyplot import *
#from scitools.std import *


plot(x, y)         # simplest command

plot(t1, y1, 'r',  # curve 1, red line
     t2, y2, 'b',  # curve 2, blue line
     t3, y3, 'o')  # curve 3, circles at data points
axis([t1[0], t1[-1], -1.1, 1.1])
legend(['model 1', 'model 2', 'measurements'])
xlabel('time');  ylabel('force')
savefig('myframe_%04d.png' % plot_counter)

Note: straight lines are drawn between each data point

Alternativ plotting of \( y=f(x) \) curves

Single SciTools plot command with keyword arguments: 

from scitools.std import *

plot(t1, y1, 'r',  # curve 1, red line
     t2, y2, 'b',  # curve 2, blue line
     t3, y3, 'o',  # curve 3, circles at data points
     axis=[t1[0], t1[-1], -1.1, 1.1],
     legend=('model 1', 'model 2', 'measurements'),
     xlabel='time', ylabel='force',
     savefig='myframe_%04d.png' % plot_counter)

Summary of making animations

  • Make a hardcopy of each plot frame (PNG or PDF format)

  • Use avconv or ffmpeg to make movie

Terminal> avconv -r 5 -i tmp_%04d.png -vcodec flv movie.flv

Array functionality

Construction Meaning
array(ld) copy list data ld to a numpy array
asarray(d) make array of data d (no data copy if already array)
zeros(n) make a float vector/array of length n, with zeros
zeros(n, int) make an int vector/array of length n with zeros
zeros((m,n)) make a two-dimensional float array with shape (m,`n`)
zeros_like(x) make array of same shape and element type as x
linspace(a,b,m) uniform sequence of m numbers in \( [a,b] \)
a.shape tuple containing a's shape
a.size total no of elements in a
len(a) length of a one-dim. array a (same as a.shape[0])
a.dtype the type of elements in a
a.reshape(3,2) return a reshaped as \( 3\times 2 \) array
a[i] vector indexing
a[i,j] two-dim. array indexing
a[1:k] slice: reference data with indices 1,\ldots,`k-1`
a[1:8:3] slice: reference data with indices 1, 4,\ldots,`7`
b = a.copy() copy an array
sin(a), exp(a), ... numpy functions applicable to arrays
c = concatenate((a, b)) c contains a with b appended
c = where(cond, a1, a2) c[i] = a1[i] if cond[i], else c[i] = a2[i]
isinstance(a, ndarray) is True if a is an array

Summarizing example: animating a function (part 1)

Goal: visualize the temperature in the ground as a function of depth (\( z \)) and time (\( t \)), displayed as a movie in time:

 
$$ T(z,t) = T_0 + Ae^{-az}\cos (\omega t - az),\quad a =\sqrt{\omega\over 2k} $$

 

First we make a general animation function for an \( f(x,t) \): 

from scitools.std import plot  # convenient for animations

def animate(tmax, dt, x, function, ymin, ymax, t0=0,
            xlabel='x', ylabel='y', filename='tmp_'):
    t = t0
    counter = 0
    while t <= tmax:
        y = function(x, t)
        plot(x, y,
             axis=[x[0], x[-1], ymin, ymax],
             title='time=%g' % t,
             xlabel=xlabel, ylabel=ylabel,
             savefig=filename + '%04d.png' % counter)
        t += dt
        counter += 1

Then we call this function with our special \( T(z,t) \) function

Summarizing example: animating a function (part 2) 

# remove old plot files:
import glob, os
for filename in glob.glob('tmp_*.png'): os.remove(filename)

def T(z, t):
    # T0, A, k, and omega are global variables
    a = sqrt(omega/(2*k))
    return T0 + A*exp(-a*z)*cos(omega*t - a*z)

k = 1E-6     # heat conduction coefficient (in m*m/s)
P = 24*60*60.# oscillation period of 24 h (in seconds)
omega = 2*pi/P
dt = P/24    # time lag: 1 h
tmax = 3*P   # 3 day/night simulation
T0 = 10      # mean surface temperature in Celsius
A = 10       # amplitude of the temperature variations (in C)
a = sqrt(omega/(2*k))
D = -(1/a)*log(0.001) # max depth
n = 501      # no of points in the z direction

z = linspace(0, D, n)
animate(tmax, dt, z, T, T0-A, T0+A, 0, 'z', 'T')

Must combine hardcopy files (like tmp_0034.png) to make video formats