Ch.9: Object-oriented programming
Aug 15, 2015
Inheritance
|
|
|
The chapter title Object-oriented programming (OO) may mean two different things
- Programming with classes (better: object-based programming)
- Programming with class hierarchies (class families)
New concept: collect classes in families (hierarchies)
- A family of closely related classes
- A key concept is inheritance: child classes can inherit attributes and methods from parent class(es) - this saves much typing and code duplication
As usual, we shall learn through examples!
OO is a Norwegian invention by Ole-Johan Dahl and Kristen Nygaard in the 1960s - one of the most important inventions in computer science, because OO is used in all big computer systems today!
Warning: OO is difficult and takes time to master
- Let ideas mature with time
- Study many examples
- OO is less important in Python than in C++, Java and C#, so the benefits of OO are less obvious in Python
- Our examples here on OO employ numerical methods for \( \int_a^b f(x)dx \), \( f'(x) \), \( u'=f(u,t) \) - make sure you understand the simplest of these numerical methods before you study the combination of OO and numerics
- Our goal: write general, reusable modules with lots of methods for numerical computing of \( \int_a^b f(x)dx \), \( f'(x) \), \( u'=f(u,t) \)
A class for straight lines
Make a class for evaluating lines \( y=c_0 + c_1x \).
class Line: def __init__(self, c0, c1): self.c0, self.c1 = c0, c1 def __call__(self, x): return self.c0 + self.c1*x def table(self, L, R, n): """Return a table with n points for L <= x <= R.""" s = '' for x in linspace(L, R, n): y = self(x) s += '%12g %12g\n' % (x, y) return s
A class for parabolas
Make a class for evaluating parabolas \( y=c_0 + c_1x + c_2x^2 \).
class Parabola: def __init__(self, c0, c1, c2): self.c0, self.c1, self.c2 = c0, c1, c2 def __call__(self, x): return self.c2*x**2 + self.c1*x + self.c0 def table(self, L, R, n): """Return a table with n points for L <= x <= R.""" s = '' for x in linspace(L, R, n): y = self(x) s += '%12g %12g\n' % (x, y) return s
This is almost the same code as class Line, except for the things with c2
Class Parabola as a subclass of Line; principles
-
Parabolacode =Linecode + a little extra with the \( c_2 \) term - Can we utilize class
Linecode in classParabola? - This is what inheritance is about!
Writing
class Parabola(Line): pass
makes Parabola inherit all methods and attributes from Line, so Parabola has attributes c0 and c1 and three methods
-
Lineis a superclass,Parabolais a subclass
(parent class, base class; child class, derived class) - Class
Parabolamust add code toLine's constructor (an extrac2attribute),__call__(an extra term), buttablecan be used unaltered - The principle is to reuse as much code in
Lineas possible and avoid duplicating code
Class Parabola as a subclass of Line; code
A subclass method can call a superclass method in this way:
superclass_name.method(self, arg1, arg2, ...)
Class Parabola as a subclass of Line:
class Parabola(Line):
def __init__(self, c0, c1, c2):
Line.__init__(self, c0, c1) # Line stores c0, c1
self.c2 = c2
def __call__(self, x):
return Line.__call__(self, x) + self.c2*x**2
What is gained?
- Class
Parabolajust adds code to the already existing code in classLine- no duplication of storingc0andc1, and computing \( c_0+c_1x \) - Class
Parabolaalso has atablemethod - it is inherited -
__init__and__call__are overridden or redefined in the subclass
Class Parabola as a subclass of Line; demo
p = Parabola(1, -2, 2)
p1 = p(2.5)
print p1
print p.table(0, 1, 3)
Output:
8.5
0 1
0.5 0.5
1 1
Exercise 1: Point out the program flow
We can check class type and class relations with isinstance(obj, type) and issubclass(subclassname, superclassname)
>>> from Line_Parabola import Line, Parabola
>>> l = Line(-1, 1)
>>> isinstance(l, Line)
True
>>> isinstance(l, Parabola)
False
>>> p = Parabola(-1, 0, 10)
>>> isinstance(p, Parabola)
True
>>> isinstance(p, Line)
True
>>> issubclass(Parabola, Line)
True
>>> issubclass(Line, Parabola)
False
>>> p.__class__ == Parabola
True
>>> p.__class__.__name__ # string version of the class name
'Parabola'
Line as a subclass of Parabola
- Subclasses are often special cases of a superclass
- A line \( c_0+c_1x \) is a special case of a parabola \( c_0+c_1x+c_2x^2 \)
- Can
Linebe a subclass ofParabola? - No problem - this is up to the programmer's choice
- Many will prefer this relation between a line and a parabola
Code when Line is a subclass of Parabola
class Parabola:
def __init__(self, c0, c1, c2):
self.c0, self.c1, self.c2 = c0, c1, c2
def __call__(self, x):
return self.c2*x**2 + self.c1*x + self.c0
def table(self, L, R, n):
"""Return a table with n points for L <= x <= R."""
s = ''
for x in linspace(L, R, n):
y = self(x)
s += '%12g %12g\n' % (x, y)
return s
class Line(Parabola):
def __init__(self, c0, c1):
Parabola.__init__(self, c0, c1, 0)
Note: __call__ and table can be reused in class Line!
Recall the class for numerical differentiation from Ch. 7
$$ f'(x) \approx {f(x+h)-f(x)\over h} $$
class Derivative:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
def __call__(self, x):
f, h = self.f, self.h # make short forms
return (f(x+h) - f(x))/h
def f(x):
return exp(-x)*cos(tanh(x))
from math import exp, cos, tanh
dfdx = Derivative(f)
print dfdx(2.0)
There are numerous formulas numerical differentiation
$$
\begin{align*}
f'(x) &= \frac{f(x+h)-f(x)}{h} + {\cal O}(h)\\
f'(x) &= \frac{f(x)-f(x-h)}{h} + {\cal O}(h)\\
f'(x) &= \frac{f(x+h)-f(x-h)}{2h} + {\cal O}(h^2)\\
f'(x) &= \frac{4}{3}\frac{f(x+h)-f(x-h)}{2h}
-\frac{1}{3}\frac{f(x+2h) - f(x-2h)}{4h} + {\cal O}(h^4)\\
f'(x) &= \frac{3}{2}\frac{f(x+h)-f(x-h)}{2h}
-\frac{3}{5}\frac{f(x+2h) - f(x-2h)}{4h} + \nonumber\\
& \frac{1}{10}\frac{f(x+3h) - f(x-3h)}{6h} + {\cal O}(h^6)\\
f'(x) &= \frac{1}{h}\left(
-\frac{1}{6}f(x+2h) + f(x+h) - \frac{1}{2}f(x) - \frac{1}{3}f(x-h)\right)
+ {\cal O}(h^3)
\end{align*}
$$
How can we make a module that offers all these formulas?
class Forward1:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
def __call__(self, x):
f, h = self.f, self.h
return (f(x+h) - f(x))/h
class Backward1:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
def __call__(self, x):
f, h = self.f, self.h
return (f(x) - f(x-h))/h
class Central2:
# same constructor
# put relevant formula in __call__
What is the problem with this type of code?
All the constructors are identical so we duplicate a lot of code.
- A general OO idea: place code common to many classes in a superclass and inherit that code
- Here: inhert constructor from superclass,
let subclasses for different differentiation formulas implement their version of__call__
Class hierarchy for numerical differentiation
class Diff:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
class Forward1(Diff):
def __call__(self, x):
f, h = self.f, self.h
return (f(x+h) - f(x))/h
class Central4(Diff):
def __call__(self, x):
f, h = self.f, self.h
return (4./3)*(f(x+h) - f(x-h)) /(2*h) - \
(1./3)*(f(x+2*h) - f(x-2*h))/(4*h)
Use of the differentiation classes
Interactive example: \( f(x)=\sin x \), compute \( f'(x) \) for \( x=\pi \)
>>> from Diff import *
>>> from math import sin
>>> mycos = Central4(sin)
>>> # compute sin'(pi):
>>> mycos(pi)
-1.000000082740371
Central4(sin) calls inherited constructor in superclass, while mycos(pi) calls __call__ in the subclass Central4
Exercise 2: Point out the program flow
A flexible main program for numerical differentiation
Suppose we want to differentiate function expressions from the command line:
Terminal> python df.py 'exp(sin(x))' Central 2 3.1
-1.04155573055
Terminal> python df.py 'f(x)' difftype difforder x
f'(x)
With eval and the Diff class hierarchy this main program can be realized in a few lines (many lines in C# and Java!):
import sys
from Diff import *
from math import *
from scitools.StringFunction import StringFunction
f = StringFunction(sys.argv[1])
difftype = sys.argv[2]
difforder = sys.argv[3]
classname = difftype + difforder
df = eval(classname + '(f)')
x = float(sys.argv[4])
print df(x)
Investigating numerical approximation errors
- We can empirically investigate the accuracy of our family of 6 numerical differentiation formulas
- Sample function: \( f(x)=\exp{(-10x)} \)
- See the book for a little program that computes the errors:
. h Forward1 Central2 Central4
6.25E-02 -2.56418286E+00 6.63876231E-01 -5.32825724E-02
3.12E-02 -1.41170013E+00 1.63556996E-01 -3.21608292E-03
1.56E-02 -7.42100948E-01 4.07398036E-02 -1.99260429E-04
7.81E-03 -3.80648092E-01 1.01756309E-02 -1.24266603E-05
3.91E-03 -1.92794011E-01 2.54332554E-03 -7.76243120E-07
1.95E-03 -9.70235594E-02 6.35795004E-04 -4.85085874E-08
Observations:
- Halving \( h \) from row to row reduces the errors by a factor of 2, 4 and 16, i.e, the errors go like \( h \), \( h^2 \), and \( h^4 \)
-
Central4has really superior accuracy compared withForward1
Alternative implementations (in the book)
- Pure Python functions
downside: more arguments to transfer, cannot apply formulas twice to get 2nd-order derivatives etc. - Functional programming
gives the same flexibility as the OO solution - One class and one common math formula
applies math notation instead of programming techniques to generalize code
These techniques are beyond scope in the course, but place OO into a bigger perspective. Might better clarify what OO is - for some.
Formulas for numerical integration
There are numerous formulas for numerical integration and all of them can be put into a common notation:
$$ \int_a^b f(x)dx \approx \sum_{i=0}^{n-1} w_i f(x_i)$$
\( w_i \): weights, \( x_i \): points (specific to a certain formula)
The Trapezoidal rule has \( h=(b-a)/(n-1) \) and
$$ x_i = a+ih, \quad w_0=w_{n-1}={h\over2},\ w_i=h\ (i\neq 0,n-1)$$
The Midpoint rule has \( h=(b-a)/n \) and
$$ x_i = a + {h\over 2} + ih,\quad w_i=h$$
More formulas
Simpson's rule has
$$
\begin{align*}
x_i &= a+ih,\quad h={b-a\over n-1}\\
w_0 &=w_{n-1}={h\over6}\\
w_i &= {h\over3}\hbox{ for }i\hbox{ even},\quad w_i={2h\over3}\hbox{ for }i\hbox{ odd}
\end{align*}
$$
Other rules have more complicated formulas for \( w_i \) and \( x_i \)
Why should these formulas be implemented in a class hierarchy?
- A numerical integration formula can be implemented as a class: \( a \), \( b \) and \( n \) are attributes and an
integratemethod evaluates the formula - All such classes are quite similar: the evaluation of \( \sum_jw_jf(x_j) \) is the same, only the definition of the points and weights differ among the classes
- Recall: code duplication is a bad thing!
- The general OO idea: place code common to many classes in a superclass and inherit that code
- Here we put \( \sum_jw_jf(x_j) \) in a superclass (method
integrate) - Subclasses extend the superclass with code specific to a math formula, i.e., \( w_i \) and \( x_i \) in a class method
construct_rule
The superclass for integration
class Integrator:
def __init__(self, a, b, n):
self.a, self.b, self.n = a, b, n
self.points, self.weights = self.construct_method()
def construct_method(self):
raise NotImplementedError('no rule in class %s' % \
self.__class__.__name__)
def integrate(self, f):
s = 0
for i in range(len(self.weights)):
s += self.weights[i]*f(self.points[i])
return s
def vectorized_integrate(self, f):
# f must be vectorized for this to work
return dot(self.weights, f(self.points))
A subclass: the Trapezoidal rule
class Trapezoidal(Integrator):
def construct_method(self):
h = (self.b - self.a)/float(self.n - 1)
x = linspace(self.a, self.b, self.n)
w = zeros(len(x))
w[1:-1] += h
w[0] = h/2; w[-1] = h/2
return x, w
Another subclass: Simpson's rule
- Simpson's rule is more tricky to implement because of different formulas for odd and even points
- Don't bother with the details of \( w_i \) and \( x_i \) in Simpson's rule now - focus on the class design!
class Simpson(Integrator):
def construct_method(self):
if self.n % 2 != 1:
print 'n=%d must be odd, 1 is added' % self.n
self.n += 1
<code for computing x and w>
return x, w
About the program flow
Let us integrate \( \int_0^2 x^2dx \) using 101 points:
def f(x):
return x*x
method = Simpson(0, 2, 101)
print method.integrate(f)
Important:
-
method = Simpson(...): this invokes the superclass constructor, which callsconstruct_methodin classSimpson -
method.integrate(f)invokes the inheritedintegratemethod, defined in classIntegrator
Exercise 3: Point out the program flow
Applications of the family of integration classes
We can empirically test out the accuracy of different integration methods Midpoint, Trapezoidal, Simpson, GaussLegendre2, ... applied to, e.g.,
$$ \int\limits_0^1 \left(1 + {1\over m}\right)t^{1\over m} dt= 1$$
- This integral is "difficult" numerically for \( m>1 \).
- Key problem: the error in numerical integration formulas is of the form \( Cn^{-r} \), mathematical theory can predict \( r \) (the "order"), but we can estimate \( r \) empirically too
- See the book for computational details
- Here we focus on the conclusions
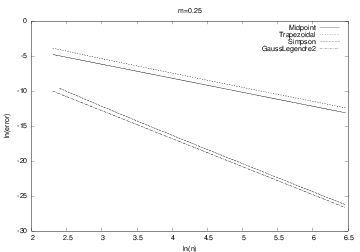
Convergence rates for \( m < 1 \) (easy case)
Simpson and Gauss-Legendre reduce the error faster than Midpoint and Trapezoidal (plot has ln(error) versus \( \ln n \))
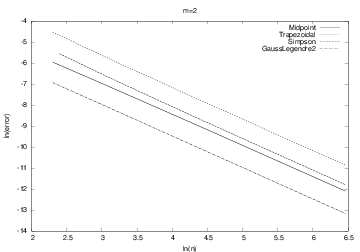
Convergence rates for \( m>1 \) (problematic case)
Simpson and Gauss-Legendre, which are theoretically "smarter" than Midpoint and Trapezoidal do not show superior behavior!
Summary of object-orientation principles
- A subclass inherits everything from the superclass
- When to use a subclass/superclass?
- if code common to several classes can be placed in a superclass
- if the problem has a natural child-parent concept
- The program flow jumps between super- and sub-classes
- It takes time to master when and how to use OO
- Study examples!
Recall the class hierarchy for differentiation
Collection of difference formulas for \( f'(x) \). For example,
$$ f'(x) \approx {f(x+h)-f(x-h)\over 2h}$$
Superclass Diff contains common code (constructor), subclasses implement various difference formulas.
class Diff:
def __init__(self, f, h=1E-5):
self.f = f
self.h = float(h)
class Central2(Diff):
def __call__(self, x):
f, h = self.f, self.h
return (f(x+h) - f(x-h))/(2*h)
Recall the class hierarchy for integration (1)
General integration formula for numerical integration:
$$ \int_a^b f(x)dx \approx \sum_{j=0}^{n-1} w_if(x_i)$$
Superclass Integrator contains common code (constructor, \( \sum_j w_if(x_i) \)), subclasses implement definition of \( w_i \) and \( x_i \).
Recall the class hierarchy for integration (2)
class Integrator:
def __init__(self, a, b, n):
self.a, self.b, self.n = a, b, n
self.points, self.weights = self.construct_method()
def integrate(self, f):
s = 0
for i in range(len(self.weights)):
s += self.weights[i]*f(self.points[i])
return s
class Trapezoidal(Integrator):
def construct_method(self):
x = linspace(self.a, self.b, self.n)
h = (self.b - self.a)/float(self.n - 1)
w = zeros(len(x)) + h
w[0] /= 2; w[-1] /= 2 # adjust end weights
return x, w
A summarizing example: Generalized reading of input data
outfile = open(filename, 'w')
from numpy import linspace
for x in linspace(a, b, n):
outfile.write('%12g %12g\n' % (x, f(x)))
outfile.close()
Read a, b, n, filename and a formula for f from...
- the command line
- interactive commands like
a=0,b=2,filename=mydat.dat - questions and answers in the terminal window
- a graphical user interface
- a file of the form
a = 0
b = 2
filename = mydat.dat
Graphical user interface
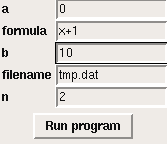
First we write the application code
from ReadInput import *
# define all input parameters as name-value pairs in a dict:
p = dict(formula='x+1', a=0, b=1, n=2, filename='tmp.dat')
# read from some input medium:
inp = ReadCommandLine(p)
# or
inp = PromptUser(p) # questions in the terminal window
# or
inp = ReadInputFile(p) # read file or interactive commands
# or
inp = GUI(p) # read from a GUI
# load input data into separate variables (alphabetic order)
a, b, filename, formula, n = inp.get_all()
# go!
About the implementation
- A superclass
ReadInputstores the dict and provides methods for getting input into program variables (get,get_all) - Subclasses read from different input sources
-
ReadCommandLine,PromptUser,ReadInputFile,GUI - See the book or
ReadInput.pyfor implementation details - For now the ideas and principles are more important than code details!