Ch.9: Object-oriented programming

Let ideas mature with time
Study many examples
OO is less important in Python than in C++, Java and C#, so the benefits of OO are less obvious in Python
Our examples here on OO employ numerical methods for $ \int_a^b f(x)dx $, $ f'(x) $, $ u'=f(u,t) $ - make sure you understand the simplest of these numerical methods before you study the combination of OO and numerics
Our goal: write general, reusable modules with lots of methods for numerical computing of $ \int_a^b f(x)dx $, $ f'(x) $, $ u'=f(u,t) $

A class for straight lines

Problem:

Make a class for evaluating lines $ y=c_0 + c_1x $.

Code:

class Line:
    def __init__(self, c0, c1):
        self.c0, self.c1 = c0, c1

    def __call__(self, x):
        return self.c0 + self.c1*x

    def table(self, L, R, n):
        """Return a table with n points for L <= x <= R."""
        s = ''
        for x in linspace(L, R, n):
            y = self(x)
            s += '%12g %12g\n' % (x, y)
        return s

A class for parabolas

Problem:

Make a class for evaluating parabolas $ y=c_0 + c_1x + c_2x^2 $.

Code:

class Parabola:
    def __init__(self, c0, c1, c2):
        self.c0, self.c1, self.c2 = c0, c1, c2

    def __call__(self, x):
        return self.c2*x**2 + self.c1*x + self.c0

    def table(self, L, R, n):
        """Return a table with n points for L <= x <= R."""
        s = ''
        for x in linspace(L, R, n):
            y = self(x)
            s += '%12g %12g\n' % (x, y)
        return s

Observation:

This is almost the same code as class Line, except for the things with c2

Class Parabola as a subclass of Line; principles

Parabola code = Line code + a little extra with the $ c_2 $ term
Can we utilize class Line code in class Parabola?
This is what inheritance is about!

Writing

class Parabola(Line):
    pass

makes Parabola inherit all methods and attributes from Line, so Parabola has attributes c0 and c1 and three methods

Line is a superclass, Parabola is a subclass
(parent class, base class; child class, derived class)
Class Parabola must add code to Line's constructor (an extra c2 attribute), __call__ (an extra term), but table can be used unaltered
The principle is to reuse as much code in Line as possible and avoid duplicating code

Class Parabola as a subclass of Line; code

A subclass method can call a superclass method in this way:

superclass_name.method(self, arg1, arg2, ...)

Class Parabola as a subclass of Line:

class Parabola(Line):
    def __init__(self, c0, c1, c2):
        Line.__init__(self, c0, c1)  # Line stores c0, c1
        self.c2 = c2

    def __call__(self, x):
        return Line.__call__(self, x) + self.c2*x**2

What is gained?

Class Parabola just adds code to the already existing code in class Line - no duplication of storing c0 and c1, and computing $ c_0+c_1x $
Class Parabola also has a table method - it is inherited
__init__ and __call__ are overridden or redefined in the subclass

Class Parabola as a subclass of Line; demo

p = Parabola(1, -2, 2)
p1 = p(2.5)
print p1
print p.table(0, 1, 3)

Output:

8.5
           0            1
         0.5          0.5
           1            1

Exercise 1: Point out the program flow

We can check class type and class relations with isinstance(obj, type) and issubclass(subclassname, superclassname)

>>> from Line_Parabola import Line, Parabola
>>> l = Line(-1, 1)
>>> isinstance(l, Line)
True
>>> isinstance(l, Parabola)
False

>>> p = Parabola(-1, 0, 10)
>>> isinstance(p, Parabola)
True
>>> isinstance(p, Line)
True

>>> issubclass(Parabola, Line)
True
>>> issubclass(Line, Parabola)
False

>>> p.__class__ == Parabola
True
>>> p.__class__.__name__   # string version of the class name
'Parabola'

Line as a subclass of Parabola

Subclasses are often special cases of a superclass
A line $ c_0+c_1x $ is a special case of a parabola $ c_0+c_1x+c_2x^2 $
Can Line be a subclass of Parabola?
No problem - this is up to the programmer's choice
Many will prefer this relation between a line and a parabola

Code when Line is a subclass of Parabola

class Parabola:
    def __init__(self, c0, c1, c2):
        self.c0, self.c1, self.c2 = c0, c1, c2

    def __call__(self, x):
        return self.c2*x**2 + self.c1*x + self.c0

    def table(self, L, R, n):
        """Return a table with n points for L <= x <= R."""
        s = ''
        for x in linspace(L, R, n):
            y = self(x)
            s += '%12g %12g\n' % (x, y)
        return s

class Line(Parabola):
    def __init__(self, c0, c1):
        Parabola.__init__(self, c0, c1, 0)

Note: __call__ and table can be reused in class Line!

Recall the class for numerical differentiation from Ch. 7

class Derivative:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

    def __call__(self, x):
        f, h = self.f, self.h      # make short forms
        return (f(x+h) - f(x))/h

def f(x):
    return exp(-x)*cos(tanh(x))

from math import exp, cos, tanh
dfdx = Derivative(f)
print dfdx(2.0)

There are numerous formulas numerical differentiation

$$ \begin{align*} f'(x) &= \frac{f(x+h)-f(x)}{h} + {\cal O}(h)\\ f'(x) &= \frac{f(x)-f(x-h)}{h} + {\cal O}(h)\\ f'(x) &= \frac{f(x+h)-f(x-h)}{2h} + {\cal O}(h^2)\\ f'(x) &= \frac{4}{3}\frac{f(x+h)-f(x-h)}{2h} -\frac{1}{3}\frac{f(x+2h) - f(x-2h)}{4h} + {\cal O}(h^4)\\ f'(x) &= \frac{3}{2}\frac{f(x+h)-f(x-h)}{2h} -\frac{3}{5}\frac{f(x+2h) - f(x-2h)}{4h} + \nonumber\\ & \frac{1}{10}\frac{f(x+3h) - f(x-3h)}{6h} + {\cal O}(h^6)\\ f'(x) &= \frac{1}{h}\left( -\frac{1}{6}f(x+2h) + f(x+h) - \frac{1}{2}f(x) - \frac{1}{3}f(x-h)\right) + {\cal O}(h^3) \end{align*} $$

How can we make a module that offers all these formulas?

It's easy:

class Forward1:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

    def __call__(self, x):
        f, h = self.f, self.h
        return (f(x+h) - f(x))/h

class Backward1:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

    def __call__(self, x):
        f, h = self.f, self.h
        return (f(x) - f(x-h))/h

class Central2:
    # same constructor
    # put relevant formula in __call__

What is the problem with this type of code?

All the constructors are identical so we duplicate a lot of code.

A general OO idea: place code common to many classes in a superclass and inherit that code
Here: inhert constructor from superclass,
let subclasses for different differentiation formulas implement their version of __call__

Class hierarchy for numerical differentiation

Superclass:

class Diff:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

Subclass for simple 1st-order forward formula:

class Forward1(Diff):
    def __call__(self, x):
        f, h = self.f, self.h
        return (f(x+h) - f(x))/h

Subclass for 4-th order central formula:

class Central4(Diff):
    def __call__(self, x):
        f, h = self.f, self.h
        return (4./3)*(f(x+h)   - f(x-h))  /(2*h) - \
               (1./3)*(f(x+2*h) - f(x-2*h))/(4*h)

Use of the differentiation classes

Interactive example: $ f(x)=\sin x $, compute $ f'(x) $ for $ x=\pi $

>>> from Diff import *
>>> from math import sin
>>> mycos = Central4(sin)
>>> # compute sin'(pi):
>>> mycos(pi)
-1.000000082740371

Central4(sin) calls inherited constructor in superclass, while mycos(pi) calls __call__ in the subclass Central4

Exercise 2: Point out the program flow

A flexible main program for numerical differentiation

Suppose we want to differentiate function expressions from the command line:

Terminal> python df.py 'exp(sin(x))' Central 2 3.1
-1.04155573055

Terminal> python df.py 'f(x)' difftype difforder x
f'(x)

With eval and the Diff class hierarchy this main program can be realized in a few lines (many lines in C# and Java!):

import sys
from Diff import *
from math import *
from scitools.StringFunction import StringFunction

f = StringFunction(sys.argv[1])
difftype = sys.argv[2]
difforder = sys.argv[3]
classname = difftype + difforder
df = eval(classname + '(f)')
x = float(sys.argv[4])
print df(x)

Investigating numerical approximation errors

We can empirically investigate the accuracy of our family of 6 numerical differentiation formulas
Sample function: $ f(x)=\exp{(-10x)} $
See the book for a little program that computes the errors:

.   h        Forward1        Central2        Central4
6.25E-02 -2.56418286E+00  6.63876231E-01 -5.32825724E-02
3.12E-02 -1.41170013E+00  1.63556996E-01 -3.21608292E-03
1.56E-02 -7.42100948E-01  4.07398036E-02 -1.99260429E-04
7.81E-03 -3.80648092E-01  1.01756309E-02 -1.24266603E-05
3.91E-03 -1.92794011E-01  2.54332554E-03 -7.76243120E-07
1.95E-03 -9.70235594E-02  6.35795004E-04 -4.85085874E-08

Observations:

Halving $ h $ from row to row reduces the errors by a factor of 2, 4 and 16, i.e, the errors go like $ h $, $ h^2 $, and $ h^4 $
Central4 has really superior accuracy compared with Forward1

Alternative implementations (in the book)

Pure Python functions
downside: more arguments to transfer, cannot apply formulas twice to get 2nd-order derivatives etc.
Functional programming
gives the same flexibility as the OO solution
One class and one common math formula
applies math notation instead of programming techniques to generalize code

These techniques are beyond scope in the course, but place OO into a bigger perspective. Might better clarify what OO is - for some.

Formulas for numerical integration

There are numerous formulas for numerical integration and all of them can be put into a common notation: $$ \int_a^b f(x)dx \approx \sum_{i=0}^{n-1} w_i f(x_i)$$ $ w_i $: weights, $ x_i $: points (specific to a certain formula)

The Trapezoidal rule has $ h=(b-a)/(n-1) $ and $$ x_i = a+ih, \quad w_0=w_{n-1}={h\over2},\ w_i=h\ (i\neq 0,n-1)$$

The Midpoint rule has $ h=(b-a)/n $ and $$ x_i = a + {h\over 2} + ih,\quad w_i=h$$

More formulas

Simpson's rule has $$ \begin{align*} x_i &= a+ih,\quad h={b-a\over n-1}\\ w_0 &=w_{n-1}={h\over6}\\ w_i &= {h\over3}\hbox{ for }i\hbox{ even},\quad w_i={2h\over3}\hbox{ for }i\hbox{ odd} \end{align*} $$

Other rules have more complicated formulas for $ w_i $ and $ x_i $

Why should these formulas be implemented in a class hierarchy?

A numerical integration formula can be implemented as a class: $ a $, $ b $ and $ n $ are attributes and an integrate method evaluates the formula
All such classes are quite similar: the evaluation of $ \sum_jw_jf(x_j) $ is the same, only the definition of the points and weights differ among the classes
Recall: code duplication is a bad thing!
The general OO idea: place code common to many classes in a superclass and inherit that code
Here we put $ \sum_jw_jf(x_j) $ in a superclass (method integrate)
Subclasses extend the superclass with code specific to a math formula, i.e., $ w_i $ and $ x_i $ in a class method construct_rule

The superclass for integration

class Integrator:
    def __init__(self, a, b, n):
        self.a, self.b, self.n = a, b, n
        self.points, self.weights = self.construct_method()

    def construct_method(self):
        raise NotImplementedError('no rule in class %s' % \
                                  self.__class__.__name__)

    def integrate(self, f):
        s = 0
        for i in range(len(self.weights)):
            s += self.weights[i]*f(self.points[i])
        return s

    def vectorized_integrate(self, f):
        # f must be vectorized for this to work
        return dot(self.weights, f(self.points))

A subclass: the Trapezoidal rule

class Trapezoidal(Integrator):
    def construct_method(self):
        h = (self.b - self.a)/float(self.n - 1)
        x = linspace(self.a, self.b, self.n)
        w = zeros(len(x))
        w[1:-1] += h
        w[0] = h/2;  w[-1] = h/2
        return x, w

Another subclass: Simpson's rule

Simpson's rule is more tricky to implement because of different formulas for odd and even points
Don't bother with the details of $ w_i $ and $ x_i $ in Simpson's rule now - focus on the class design!

class Simpson(Integrator):

    def construct_method(self):
        if self.n % 2 != 1:
            print 'n=%d must be odd, 1 is added' % self.n
            self.n += 1

        <code for computing x and w>
        return x, w

About the program flow

Let us integrate $ \int_0^2 x^2dx $ using 101 points:

def f(x):
    return x*x

method = Simpson(0, 2, 101)
print method.integrate(f)

Important:

method = Simpson(...): this invokes the superclass constructor, which calls construct_method in class Simpson
method.integrate(f) invokes the inherited integrate method, defined in class Integrator

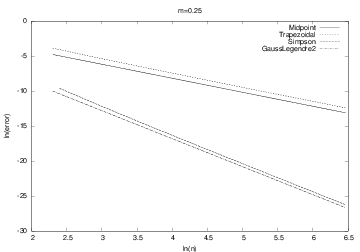
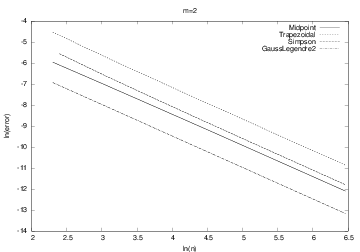
Exercise 3: Point out the program flow

Applications of the family of integration classes

We can empirically test out the accuracy of different integration methods Midpoint, Trapezoidal, Simpson, GaussLegendre2, ... applied to, e.g., $$ \int\limits_0^1 \left(1 + {1\over m}\right)t^{1\over m} dt= 1$$

This integral is "difficult" numerically for $ m>1 $.
Key problem: the error in numerical integration formulas is of the form $ Cn^{-r} $, mathematical theory can predict $ r $ (the "order"), but we can estimate $ r $ empirically too
See the book for computational details
Here we focus on the conclusions

Convergence rates for $ m < 1 $ (easy case)

Simpson and Gauss-Legendre reduce the error faster than Midpoint and Trapezoidal (plot has ln(error) versus $ \ln n $)

Convergence rates for $ m>1 $ (problematic case)

Simpson and Gauss-Legendre, which are theoretically "smarter" than Midpoint and Trapezoidal do not show superior behavior!

Summary of object-orientation principles

A subclass inherits everything from the superclass
When to use a subclass/superclass?

if code common to several classes can be placed in a superclass
if the problem has a natural child-parent concept

The program flow jumps between super- and sub-classes
It takes time to master when and how to use OO
Study examples!

Recall the class hierarchy for differentiation

Mathematical principles:

Collection of difference formulas for $ f'(x) $. For example, $$ f'(x) \approx {f(x+h)-f(x-h)\over 2h}$$

Superclass Diff contains common code (constructor), subclasses implement various difference formulas.

Implementation example (superclass and one subclass).

class Diff:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

class Central2(Diff):
    def __call__(self, x):
        f, h = self.f, self.h
        return (f(x+h) - f(x-h))/(2*h)

Recall the class hierarchy for integration (1)

Mathematical principles:

General integration formula for numerical integration: $$ \int_a^b f(x)dx \approx \sum_{j=0}^{n-1} w_if(x_i)$$

Superclass Integrator contains common code (constructor, $ \sum_j w_if(x_i) $), subclasses implement definition of $ w_i $ and $ x_i $.

Recall the class hierarchy for integration (2)

Implementation example (superclass and one subclass):

 class Integrator:
    def __init__(self, a, b, n):
        self.a, self.b, self.n = a, b, n
        self.points, self.weights = self.construct_method()

    def integrate(self, f):
        s = 0
        for i in range(len(self.weights)):
            s += self.weights[i]*f(self.points[i])
        return s

 class Trapezoidal(Integrator):
    def construct_method(self):
        x = linspace(self.a, self.b, self.n)
        h = (self.b - self.a)/float(self.n - 1)
        w = zeros(len(x)) + h
        w[0] /= 2;  w[-1] /= 2  # adjust end weights
        return x, w

A summarizing example: Generalized reading of input data

Write a table of $ x\in [a,b] $ and $ f(x) $ to file:

outfile = open(filename, 'w')
from numpy import linspace
for x in linspace(a, b, n):
    outfile.write('%12g  %12g\n' % (x, f(x)))
outfile.close()

We want flexible input:

Read a, b, n, filename and a formula for f from...

the command line
interactive commands like a=0, b=2, filename=mydat.dat
questions and answers in the terminal window
a graphical user interface
a file of the form

a = 0
b = 2
filename = mydat.dat

Graphical user interface

First we write the application code

Desired usage:

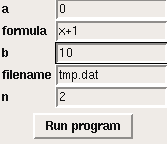
from ReadInput import *

# define all input parameters as name-value pairs in a dict:
p = dict(formula='x+1', a=0, b=1, n=2, filename='tmp.dat')

# read from some input medium:
inp = ReadCommandLine(p)
# or
inp = PromptUser(p)     # questions in the terminal window
# or
inp = ReadInputFile(p)  # read file or interactive commands
# or
inp = GUI(p)            # read from a GUI

# load input data into separate variables (alphabetic order)
a, b, filename, formula, n = inp.get_all()

# go!

About the implementation

A superclass ReadInput stores the dict and provides methods for getting input into program variables (get, get_all)
Subclasses read from different input sources
ReadCommandLine, PromptUser, ReadInputFile, GUI
See the book or ReadInput.py for implementation details
For now the ideas and principles are more important than code details!