Ch.2: Loops and lists

We know how to make one line in the table:

C = -20
F = 9.0/5*C + 32
print C, F

We can just repeat these statements:

C = -20;  F = 9.0/5*C + 32;  print C, F
C = -15;  F = 9.0/5*C + 32;  print C, F
...
C =  35;  F = 9.0/5*C + 32;  print C, F
C =  40;  F = 9.0/5*C + 32;  print C, F

Very boring to write, easy to introduce a misprint
When programming becomes boring, there is usually a construct that automates the writing!
The computer is extremely good at performing repetitive tasks
For this purpose we use loops

The while loop makes it possible to repeat almost similar tasks

A while loop executes repeatedly a set of statements as long as a boolean condition is true

while condition:
    <statement 1>
    <statement 2>
    ...
<first statement after loop>

All statements in the loop must be indented!
The loop ends when an unindented statement is encountered

The while loop for making a table

print '------------------' # table heading
C = -20                    # start value for C
dC = 5                     # increment of C in loop
while C <= 40:             # loop heading with condition
    F = (9.0/5)*C + 32     # 1st statement inside loop
    print C, F             # 2nd statement inside loop
    C = C + dC             # last statement inside loop
print '------------------' # end of table line

The program flow in a while loop

Boolean expressions are true or false

An expression with value true or false is called a boolean expression. Examples: \( C=40 \), \( C\neq 40 \), \( C\geq 40 \), \( C>40 \), \( C < 40 \).

C == 40  # note the double ==, C = 40 is an assignment!
C != 40
C >= 40
C >  40
C <  40

We can test boolean expressions in a Python shell:

>>> C = 41
>>> C != 40
True
>>> C < 40
False
>>> C == 41
True

Combining boolean expressions

Several conditions can be combined with and/or:

while condition1 and condition2:
    ...

while condition1 or condition2:
    ...

Rule 1: C1 and C2 is True if both C1 and C2 are True

Rule 2: C1 or C2 is True if one of C1 or C2 is True

>>> x = 0;  y = 1.2
>>> x >= 0 and y < 1
False
>>> x >= 0 or y < 1
True
>>> x > 0 or y > 1
True
>>> x > 0 or not y > 1
False
>>> -1 < x <= 0   #  -1 < x and x <= 0
True
>>> not (x > 0 or y > 0)
False

Lists are objects for storing a sequence of things (objects)

So far, one variable has referred to one number (or string), but sometimes we naturally have a collection of numbers, say degrees \( -20, -15, -10, -5, 0, \ldots, 40 \)

Simple solution: one variable for each value

C1 = -20
C2 = -15
C3 = -10
...
C13 = 40

Stupid and boring solution if we have many values!

Better: a set of values can be collected in a list

C = [-20, -15, -10, -5, 0, 5, 10, 15, 20, 25, 30, 35, 40]

Now there is one variable, C, holding all the values

List operations: initialization and indexing

Initialize with square brackets and comma between the Python objects:

L1 = [-91, 'a string', 7.2, 0]

Elements are accessed via an index: L1[3] (index=3).

List indices start at 0: 0, 1, 2, ... len(L1)-1.

>>> mylist = [4, 6, -3.5]
>>> print mylist[0]
4
>>> print mylist[1]
6
>>> print mylist[2]
-3.5
>>> len(mylist)  # length of list
3

List operations: append, extend, insert, delete

>>> C = [-10, -5, 0, 5, 10, 15, 20, 25, 30]
>>> C.append(35)   # add new element 35 at the end
>>> C
[-10, -5, 0, 5, 10, 15, 20, 25, 30, 35]
>>> C = C + [40, 45]     # extend C at the end
>>> C
[-10, -5, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
>>> C.insert(0, -15)     # insert -15 as index 0
>>> C
[-15, -10, -5, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
>>> del C[2]             # delete 3rd element
>>> C
[-15, -10, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
>>> del C[2]             # delete what is now 3rd element
>>> C
[-15, -10, 5, 10, 15, 20, 25, 30, 35, 40, 45]
>>> len(C)               # length of list
11

List operations: search for elements, negative indices

>>> C.index(10)   # index of the first element with value 10
3
>>> 10 in C       # is 10 an element in C?
True
>>> C[-1]         # the last list element
45
>>> C[-2]         # the next last list element
40
>>> somelist = ['book.tex', 'book.log', 'book.pdf']
>>> texfile, logfile, pdf = somelist  # assign directly to variables
>>> texfile
'book.tex'
>>> logfile
'book.log'
>>> pdf
'book.pdf'

Loop over elements in a list with a for loop

Use a for loop to loop over a list and process each element:

As with while loops, the statements in the loop must be indented!

Simulate a for loop by hand

Making a table with a for loop

Table of Celsius and Fahreheit degrees:

Cdegrees = [-20, -15, -10, -5, 0, 5, 10, 15,
             20, 25, 30, 35, 40]
for C in Cdegrees:
    F = (9.0/5)*C + 32
    print C, F

Note: print C, F gives ugly output. Use printf syntax to nicely format the two columns:

print '%5d %5.1f' % (C, F)

Output:

-20  -4.0
-15   5.0
-10  14.0
 -5  23.0
  0  32.0
  ......
 35  95.0
 40 104.0

A for loop can always be translated to a while loop

The for loop

for element in somelist:
    # process element

can always be transformed to a corresponding while loop

index = 0
while index < len(somelist):
    element = somelist[index]
    # process element
    index += 1

But not all while loops can be expressed as for loops!

While loop version of the for loop for making a table

Cdegrees = [-20, -15, -10, -5, 0, 5, 10,
            15, 20, 25, 30, 35, 40]
index = 0
while index < len(Cdegrees):
    C = Cdegrees[index]
    F = (9.0/5)*C + 32
    print '%5d %5.1f' % (C, F)
    index += 1

Implement a mathematical sum via a loop

N = 14

S = 0
for i in range(1, N+1):
    S += i**2

Or (less common):

S = 0
i = 1
while i <= N:
    S += i**2
    i += 1

Mathematical sums appear often so remember the implementation!

Storing the table columns as lists

Let us put all the Fahrenheit values in a list as well:

print Fdegrees results in

[-4.0, 5.0, 14.0, 23.0, 32.0, 41.0, 50.0, 59.0,
 68.0, 77.0, 86.0, 95.0, 104.0]

For loop with list indices

For loops usually loop over list values (elements):

for element in somelist:
    # process variable element

We can alternatively loop over list indices:

for i in range(0, len(somelist), 1):
    element = somelist[i]
    # process element or somelist[i] directly

range(start, stop, inc) generates a list of integers start, start+inc, start+2*inc, and so on up to, but not including, stop. range(stop) is short for range(0, stop, 1).

>>> range(3)         # = range(0, 3, 1)
[0, 1, 2]
>>> range(2, 8, 3)
[2, 5]

How can we change the elements in a list?

Say we want to add 2 to all numbers in a list:

>>> v = [-1, 1, 10]
>>> for e in v:
...     e = e + 2
...
>>> v
[-1, 1, 10]   # unaltered!!

Changing a list element requires assignment to an indexed element

What is the problem?

Inside the loop, e is an ordinary (int) variable, first time e becomes 1, next time e becomes 3, and then 12 - but the list v is unaltered

Solution: must index a list element to change its value:

>>> v[1] = 4    # assign 4 to 2nd element (index 1) in v
>>> v
[-1, 4, 10]
>>>
>>> for i in range(len(v)):
...     v[i] = v[i] + 2
...
>>> v
[1, 6, 12]

List comprehensions: compact creation of lists

Example: compute two lists in a for loop.

n = 16
Cdegrees = [];  Fdegrees = []  # empty lists

for i in range(n):
    Cdegrees.append(-5 + i*0.5)
    Fdegrees.append((9.0/5)*Cdegrees[i] + 32)

Python has a compact construct, called list comprehension, for generating lists from a for loop:

Cdegrees = [-5 + i*0.5 for i in range(n)]
Fdegrees = [(9.0/5)*C + 32 for C in Cdegrees]

General form of a list comprehension:

somelist = [expression for element in somelist]

where expression involves element

Interactive demonstration of list comprehensions

Traversing multiple lists simultaneously with zip

Can we one loop running over two lists?

Solution 1: loop over indices

for i in range(len(Cdegrees)):
    print Cdegrees[i], Fdegrees[i]

Solution 2: use the zip construct (more "Pythonic"):

for C, F in zip(Cdegrees, Fdegrees):
    print C, F

Example with three lists:

>>> l1 = [3, 6, 1];  l2 = [1.5, 1, 0];  l3 = [9.1, 3, 2]
>>> for e1, e2, e3 in zip(l1, l2, l3):
...     print e1, e2, e3
...
3 1.5 9.1
6 1 3
1 0 2

Nested lists: list of lists

A list can contain any object, also another list
Instead of storing a table as two separate lists (one for each column), we can stick the two lists together in a new list:

Cdegrees = range(-20, 41, 5)
Fdegrees = [(9.0/5)*C + 32 for C in Cdegrees]

table1 = [Cdegrees, Fdegrees]  # list of two lists

print table1[0]     # the Cdegrees list
print table1[1]     # the Fdegrees list
print table1[1][2]  # the 3rd element in Fdegrees

Table of columns vs table of rows

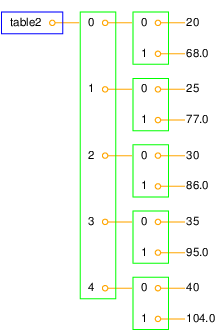
The previous table = [Cdegrees,Fdegrees] is a table of (two) columns
Let us make a table of rows instead, each row is a [C,F] pair:

table2 = []
for C, F in zip(Cdegrees, Fdegrees):
    row = [C, F]
    table2.append(row)

# more compact with list comprehension:
table2 = [[C, F] for C, F in zip(Cdegrees, Fdegrees)]

print table2

[[-20, -4.0], [-15, 5.0], ......., [40, 104.0]]

Iteration over a nested list:

for C, F in table2:
    # work with C and F from a row in table2

# or
for row in table2:
    C, F = row
    ...

Illustration of table of columns

Illustration of table of rows

Extracting sublists (or slices)

We can easily grab parts of a list:

>>> A = [2, 3.5, 8, 10]
>>> A[2:]   # from index 2 to end of list
[8, 10]

>>> A[1:3]  # from index 1 up to, but not incl., index 3
[3.5, 8]

>>> A[:3]   # from start up to, but not incl., index 3
[2, 3.5, 8]

>>> A[1:-1] # from index 1 to next last element
[3.5, 8]

>>> A[:]    # the whole list
[2, 3.5, 8, 10]

Note: sublists (slices) are copies of the original list!

What does this code snippet do?

for C, F in table2[Cdegrees.index(10):Cdegrees.index(35)]:
    print '%5.0f %5.1f' % (C, F)

This is a for loop over a sublist of table2
Sublist indices: Cdegrees.index(10), Cdegrees.index(35), i.e., the indices corresponding to elements 10 and 35

Output:

Iteration over general nested lists

List with many indices: somelist[i1][i2][i3]...

Loops over list indices:

for i1 in range(len(somelist)):
    for i2 in range(len(somelist[i1])):
        for i3 in range(len(somelist[i1][i2])):
            for i4 in range(len(somelist[i1][i2][i3])):
                value = somelist[i1][i2][i3][i4]
                # work with value

Loops over sublists:

for sublist1 in somelist:
    for sublist2 in sublist1:
        for sublist3 in sublist2:
            for sublist4 in sublist3:
                value = sublist4
                # work with value

Iteration over a specific nested list

Question.

How can we index element with value 5?

Tuples are constant lists

Tuples are constant lists that cannot be changed:

>>> t = (2, 4, 6, 'temp.pdf')    # define a tuple
>>> t =  2, 4, 6, 'temp.pdf'     # can skip parenthesis
>>> t[1] = -1
...
TypeError: object does not support item assignment

>>> t.append(0)
...
AttributeError: 'tuple' object has no attribute 'append'

>>> del t[1]
...
TypeError: object doesn't support item deletion

Tuples can do much of what lists can do:

>>> t = t + (-1.0, -2.0)           # add two tuples
>>> t
(2, 4, 6, 'temp.pdf', -1.0, -2.0)
>>> t[1]                           # indexing
4
>>> t[2:]                          # subtuple/slice
(6, 'temp.pdf', -1.0, -2.0)
>>> 6 in t                         # membership
True

Why tuples when lists have more functionality?

Tuples are constant and thus protected against accidental changes
Tuples are faster than lists
Tuples are widely used in Python software
(so you need to know about them!)
Tuples (but not lists) can be used as keys is dictionaries
(more about dictionaries later)

Key topics from this chapter

Summary of loops, lists and tuples

While loops and for loops:

while condition:
    <block of statements>

for element in somelist:
    <block of statements>

Lists and tuples:

mylist  = ['a string', 2.5, 6, 'another string']
mytuple = ('a string', 2.5, 6, 'another string')
mylist[1]  = -10
mylist.append('a third string')
mytuple[1] = -10  # illegal: cannot change a tuple

List functionality

Construction	Meaning
`a = []`	initialize an empty list
`a = [1, 4.4, 'run.py']`	initialize a list
`a.append(elem)`	add `elem` object to the end
`a + [1,3]`	add two lists
`a.insert(i, e)`	insert element `e` before index `i`
`a[3]`	index a list element
`a[-1]`	get last list element
`a[1:3]`	slice: copy data to sublist (here: index 1, 2)
`del a[3]`	delete an element (index `3`)
`a.remove(e)`	remove an element with value `e`
`a.index('run.py')`	find index corresponding to an element's value
`'run.py' in a`	test if a value is contained in the list
`a.count(v)`	count how many elements that have the value `v`
`len(a)`	number of elements in list `a`
`min(a)`	the smallest element in `a`
`max(a)`	the largest element in `a`
`sum(a)`	add all elements in `a`
`sorted(a)`	return sorted version of list `a`
`reversed(a)`	return reversed sorted version of list `a`
`b[3][0][2]`	nested list indexing
`isinstance(a, list)`	is `True` if `a` is a list
`type(a) is list`	is `True` if `a` is a list

A summarizing example; problem

src/misc/Oxford_sun_hours.txt: data of the no of sun hours in Oxford, UK, for every month since Jan, 1929:

[
[43.8, 60.5, 190.2, ...],
[49.9, 54.3, 109.7, ...],
[63.7, 72.0, 142.3, ...],
...
]

Tasks:

Compute the average number of sun hours for each month during the total data period (1929–2009),
Which month has the best weather according to the means found in the preceding task?
For each decade, 1930-1939, 1949-1949, \( \ldots \), 2000-2009, compute the average number of sun hours per day in January and December

A summarizing example; program (task 1)

data = [
[43.8, 60.5, 190.2, ...],
[49.9, 54.3, 109.7, ...],
[63.7, 72.0, 142.3, ...],
...
]
monthly_mean = [0]*12
for month in range(1, 13):
    m = month - 1   # corresponding list index (starts at 0)
    s = 0           # sum
    n = 2009 - 1929 + 1  # no of years
    for year in range(1929, 2010):
        y = year - 1929  # corresponding list index (starts at 0)
        s += data[y][m]
    monthly_mean[m] = s/n
month_names = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
               'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
# nice printout:
for name, value in zip(month_names, monthly_mean):
    print '%s: %.1f' % (name, value)

A summarizing example; program (task 2)

max_value = max(monthly_mean)
month = month_names[monthly_mean.index(max_value)]
print '%s has best weather with %.1f sun hours on average' % \
      (month, max_value)

max_value = -1E+20
for i in range(len(monthly_mean)):
    value = monthly_mean[i]
    if value > max_value:
        max_value = value
        max_i = i  # store index too
print '%s has best weather with %.1f sun hours on average' % \
      (month_names[max_i], max_value)

A summarizing example; program (task 3)

decade_mean = []
for decade_start in range(1930, 2010, 10):
    Jan_index = 0; Dec_index = 11  # indices
    s = 0
    for year in range(decade_start, decade_start+10):
        y = year - 1929  # list index
        print data[y-1][Dec_index] + data[y][Jan_index]
        s += data[y-1][Dec_index] + data[y][Jan_index]
    decade_mean.append(s/(20.*30))
for i in range(len(decade_mean)):
    print 'Decade %d-%d: %.1f' % \
          (1930+i*10, 1939+i*10, decade_mean[i])

Complete code: src/looplist/sun_data.py

Using a debugger to trace the execution

A debugger is a program that can be used to inspect and understand programs. Example:

In [1]: run -d some_program.py
ipdb> continue  # or just c (go to first statement)
1---> 1 g = 9.81;  v0 = 5
      2 dt = 0.05
      3
ipdb> step  # or just s (execute next statement)
ipdb> print g
Out[1]: 9.8100000000000005
ipdb> list  # or just l (list parts of the program)
1     1 g = 9.81;  v0 = 5
----> 2 dt = 0.05
      3
      4 def y(t):
      5     return v0*t - 0.5*g*t**2
      6
ipdb> break 15   # stop program at line 15
ipdb> c          # continue to next break point

How to find Python info

The book contains only fragments of the Python language
(intended for real beginners!)
These slides are even briefer, so you will need to look up more Python information
Primary reference: The official Python documentation at docs.python.org
Very useful: The Python Library Reference, especially the index
Example: what can I find in the math module?

Go to the Python Library Reference, click index
Go to M
find math (module), click on the link

Alternative: run pydoc math in the terminal window (briefer description)