Ch.4: User input and error handling

v0 = 5
g = 9.81
t = 0.6
y = v0*t - 0.5*g*t**2
print y

Note:

Input data ($ v_0 $, $ t $) are hardcoded (explicitly set)
Changing input data requires editing
This is considered bad programming
(because editing programs may easily introduce errors!)
Rule: read input from user - avoid editing a correct program

How do professional programs get their input?

Consider a web browser: how do you specify a web address? How do you change the font?
You don't need to go into the program and edit it...

How can we specify input data in programs?

Hardcode values
Ask the user questions and read answers
Read command-line arguments
Read data from a file

Getting input from questions and anwsers

Sample program:

C = 21; F = (9.0/5)*C + 32; print F

Idea: let the program ask the user a question "C=?", read the user's answer, assign that answer to the variable C.

C = raw_input('C=? ')   # C becomes a string
C = float(C)            # convert to float so we can compute
F = (9./5)*C + 32
print F

Running in a terminal window:

Terminal> python c2f_qa.py
C=? 21
69.8

Another example: print the n first even numbers

n = int(raw_input('n=? '))

for i in range(2, 2*n+1, 2):
    print i

# or:
print range(2, 2*n+1, 2)

# or:
for i in range(1, n+1):
    print 2*i

Command-line arguments are words written after the program name

Examples on command-line arguments:

Terminal> python myprog.py arg1 arg2 arg3 ...
Terminal> cp -r yourdir ../mydir
Terminal> ls -l

Unix programs (rm, ls, cp, ...) make heavy use of command-line arguments, (see e.g. man ls). We shall do the same.

How to use a command-line argument in our sample program

C = 21; F = (9.0/5)*C + 32; print F

The user wants to specify C as a command-line argument after the name of the program when we run the program:

Terminal> python c2f_cml.py 21
69.8

Command-line arguments are the "words" after the program name, and they are stored in the list sys.argv:

import sys
C = float(sys.argv[1])   # read 1st command-line argument
F = 9.0*C/5 + 32
print F

Command-line arguments are separated by blanks

Here is another program print_cml.py:

import sys; print sys.argv[1:]

Demonstrations:

Terminal> python print_cml.py 21 string with blanks 1.3
['21', 'string', 'with', 'blanks', '1.3']

Terminal> python print_cml.py 21 "string with blanks" 1.3
['21', 'string with blanks', '1.3']

Note 1: use quotes, as in "string with blanks", to override the rule that command-line arguments are separate by blanks.

Note 2: all list elements are surrounded by quotes, demonstrating that command-line arguments are strings.

The magic eval function turns a string into live code

eval(s) evaluates a string object s as if the string had been written directly into the program

>>> s = '1+2'
>>> r = eval(s)
>>> r
3
>>> type(r)
<type 'int'>

>>> r = eval('[1, 6, 7.5] + [1, 2]')
>>> r
[1, 6, 7.5, 1, 2]
>>> type(r)
<type 'list'>

Note: be careful with eval and string values

We want r = 'math programming'. Writing just

r = eval('math programming')

is the same as writing

r = math programming

which is an invalid expression and illegal syntax.

Remedy: must put the string inside quotes:

s = "'math programming'"
r = eval(s)                # r becomes 'math programming'

With eval, a little program (add_input.py) can do much...

Program:

i1 = eval(raw_input('Give input: '))
i2 = eval(raw_input('Give input: '))
r = i1 + i2
print '%s + %s becomes %s\nwith value %s' % \
      (type(i1), type(i2), type(r), r)

We can add integer and float:

Terminal> python add_input.py
operand 1: 1
operand 2: 3.0
<type 'int'> + <type 'float'> becomes <type 'float'>
with value 4

or two lists:

Terminal> python add_input.py
operand 1: [1,2]
operand 2: [-1,0,1]
<type 'list'> + <type 'list'> becomes <type 'list'>
with value [1, 2, -1, 0, 1]

This great flexibility also quickly breaks programs...

Terminal> python add_input.py
operand 1: (1,2)
operand 2: [3,4]
Traceback (most recent call last):
  File "add_input.py", line 3, in <module>
    r = i1 + i2
TypeError: can only concatenate tuple (not "list") to tuple

Terminal> python add_input.py
operand 1: one
Traceback (most recent call last):
  File "add_input.py", line 1, in <module>
    i1 = eval(raw_input('operand 1: '))
  File "<string>", line 1, in <module>
NameError: name 'one' is not defined

Terminal> python add_input.py
operand 1: 4
operand 2: 'Hello, World!'
Traceback (most recent call last):
  File "add_input.py", line 3, in <module>
    r = i1 + i2
TypeError: unsupported operand type(s) for +: 'int' and 'str'

A similar magic function: exec

eval(s) evaluates an expression s
eval('r = 1+1') is illegal because this is a statement, not only an expression
...but we can use exec to turn one or more complete statements into live code:

statement = 'r = 1+1'   # store statement in a string
exec(statement)
print r                 # prints 2

For longer code we can use multi-line strings:

somecode = '''
def f(t):
    term1 = exp(-a*t)*sin(w1*x)
    term2 = 2*sin(w2*x)
    return term1 + term2
'''
exec(somecode)  # execute the string as Python code

exec can be used for building a function at run-time

Embed user's formula in a Python function:

formula = raw_input('Write a formula involving x: ')
code = """
def f(x):
    return %s
""" % formula
from math import *  # make sure we have sin, cos, log, etc
exec(code)          # turn string formula into live function

# Ask the user for x values and evaluate f(x)
x = 0
while x is not None:
    x = eval(raw_input('Give x (None to quit): '))
    if x is not None:
        y = f(x)
        print 'f(%g)=%g' % (x, y)

While the program is running, the user types a formula, which becomes a function, the user gives x values until the answer is None, and the program evaluates the function f(x). Note: the programmer knows nothing about the user's choice of f(x) when she writes the program (!).

We can run the program in the Python Online Tutor

StringFunction: turn string formulas into Python functions

It is common for programs to read formulas and turn them into functions so we have made a special tool for this purpose:

>>> from scitools.std import StringFunction
>>> formula = 'exp(x)*sin(x)'
>>> f = StringFunction(formula)
>>> f(0)
0.0
>>> from math import pi
>>> f(pi)
2.8338239229952166e-15
>>> print str(f)
exp(x)*sin(x)

The function can also have parameters: $ g(t) = Ae^{-at}\sin (\omega x) $

g = StringFunction('A*exp(-a*t)*sin(omega*x)',
    independent_variable='t', A=1, a=0.1, omega=pi, x=5)
print g(1.2)
g.set_parameters(A=2, x=10)
print g(1.2)

Example: program for numerical differentiation

Usage:

Terminal> python diff.py 'exp(x)*sin(x)' 3.4
Numerical derivative: -36.6262969164

Differentiate $ e^x\sin x $ at $ x=3.4 $ numerically.

Implementation:

$$ f'(x)\approx \frac{f(x+h)-f(x-h)}{2h}\quad (h\mbox{ small}) $$

import sys
from scitools.std import StringFunction
f = StringFunction(sys.argv[1], independent_variable='x')
x = float(sys.argv[2])

def numerical_derivative(f, x, h=1E-5):
    return (f(x+h) - f(x-h))/(2*h)

print 'Numerical derivative:', numerical_derivative(f, x)

We can extend the program to also include symbolic differentiation

Terminal> python diff.py 'exp(x)*sin(x)' 3.4
Numerical derivative: -36.6262969164
Exact derivative: -36.6262969154476 (error=9.390E-10)
Formula for the derivative: exp(x)*sin(x) + exp(x)*cos(x)

Program extension:

import sympy as sym
x_value = x   # store the value of x; x will be used as symbol
x = sym.symbols('x')  # need x as symbol
formula = sym.sympify(str(f))  # turn f into sympy expression

# Differentiate formula wrt symbol x
dfdx = sym.diff(formula, x)
# Substitute symbol x by x_value
dfdx_value = dfdx.subs(x, x_value)

print 'Exact derivative:', dfdx_value, '(error=%.3E)' % \
      (dfdx_value - numerical_derivative(f, x_value))
print 'Formula for the derivative:', dfdx

Example on reading 4 parameters from the command line

Input data: $ s_0 $ (initial location), $ v_0 $ (initial velocity), $ a $ (constant acceleration) and $ t $ (time)

Specify $ s_0=1 $ m, $ v_0=1 $ m/s, $ a=0.5 $ $\hbox{m/s}^2$, and $ t=3 $ s on the command line:

Terminal> python location_cml.py 1 1 0.5 3
6.25

Program:

import sys
s0 = float(sys.argv[1])
v0 = float(sys.argv[2])
a  = float(sys.argv[3])
t  = float(sys.argv[4])
s  = s0 + v0*t + 0.5*a*t*t
print s

Command-line arguments with options

Many programs, especially on Unix systems, take a set of command-line arguments of the form --option value

Terminal> python location.py --v0 1 --t 3 --s0 1 --a 0.5
Terminal> python location.py --t 3

The latter run relies on default values for v0, s0, and a: we provide only the values we want to change.

Such option-value pairs make it easier to understand what the input is (cf. keyword arguments).

Programming option-value pairs with the argparse module

import argparse
parser = argparse.ArgumentParser()

# Define command-line arguments
parser.add_argument('--v0', '--initial_velocity', type=float,
                    default=0.0, help='initial velocity')

parser.add_argument('--s0', '--initial_position', type=float,
                    default=0.0, help='initial position')

parser.add_argument('--a', '--acceleration', type=float,
                    default=1.0, help='acceleration')

parser.add_argument('--t', '--time', type=float,
                    default=1.0, help='time')

# Read the command line and interpret the arguments
args = parser.parse_args()

# Extract values
s = args.s0 + args.v0*t + 0.5*args.a*args.t**2
# or
s0 = args.s0; v0 = args.v0; a = args.a; t = args.t
s = s0 + v0*t + 0.5*a*t**2

The program has long and short command-line arguments

Can use short or long options:

Terminal> python location.py --v0 1.2 --t 0.2
Terminal> python location.py --initial_velocity 1.2 --time 0.2

Graphical user interfaces

Most programs today fetch input data from graphical user interfaces (GUI), consisting of windows and graphical elements on the screen: buttons, menus, text fields, etc.
Why don't we learn to make such type of programs?

GUI demands much extra complicated programming
Experienced users often prefer command-line input
Programs with command-line or file input can easily be combined with each other, this is difficult with GUI-based programs

Assertion: command-line input will probably fill all your needs in university courses
But let's have a look at GUI programming!

A graphical Celsius-Fahrenheit conversion program

The Celsius degrees can be filled in as a number in a field
Clicking the "is" button computes the corresponding Fahrenheit temperature

The GUI code

from Tkinter import *
root = Tk()
C_entry = Entry(root, width=4)
C_entry.pack(side='left')
Cunit_label = Label(root, text='Celsius')
Cunit_label.pack(side='left')

def compute():
    C = float(C_entry.get())
    F = (9./5)*C + 32
    F_label.configure(text='%g' % F)

compute = Button(root, text=' is ', command=compute)
compute.pack(side='left', padx=4)

F_label = Label(root, width=4)
F_label.pack(side='left')
Funit_label = Label(root, text='Fahrenheit')
Funit_label.pack(side='left')

root.mainloop()

Reading data from files

Scientific data are often available in files. We want to read the data into objects in a program to compute with the data.

Example on a data file.

One number on each line. How can we read these numbers?

Reading a file line by line

Basic file reading:

infile = open('data.txt', 'r')    # open file
for line in infile:
    # do something with line
infile.close()                    # close file

Compute the mean values of the numbers in the file:

infile = open('data.txt', 'r')    # open file
mean = 0
for line in infile:
    number = float(line)          # line is string
    mean = mean + number
mean = mean/len(lines)
print mean

Alternative ways to read a file

Read all lines at once into a list of strings (lines):

lines = infile.readlines()
for line in lines:
    # process line
infile.close()

The modern with statement:

with open('data.txt', 'r') as infile:
    for line in infile:
        # process line

The old-fashioned while construction:

while True:
    line = infile.readline()
    if not line:
        break
    # process line
infile.close()

Reading the whole file into a string:

text = infile.read()
# process the string text

Demo of file reading

File:

Line 1. Line 2. Line 3. Line 4.

Session:

>>> infile = open('tmp.txt', 'r')
>>> lines = infile.readlines()  # read all lines
>>> lines
['Line 1.\n', 'Line 2.\n', 'Line 3.\n', 'Line 4.\n']
>>> infile.readline()  # no more to read
''
>>> infile = open('tmp.txt', 'r')
>>> infile.readline()    # read one line
'Line 1.\n'
>>> infile.readline()    # read next line
'Line 2.\n'
>>> for line in infile:  # read the next lines to the end
...     print line
...
Line 3.
Line 4.

More demo of file reading and string splitting

>>> infile = open('tmp.txt', 'r')
>>> filestr = infile.read()
>>> filestr
'Line 1.\nLine 2.\nLine 3.\nLine 4.\n'

>>> filestr.split()  # split out all words
['Line', '1.', 'Line', '2.', 'Line', '3.', 'Line', '4.']

>>> line = 'Line 3.\n'
>>> line.split()
['Line', '3.']
>>> line.split('e')
['Lin', ' 3.\n']

Most data files contain text mixed with numbers

File with data about rainfall:

Average rainfall (in mm) in Rome: 1188 months between 1782 and 1970
Jan  81.2
Feb  63.2
Mar  70.3
Apr  55.7
May  53.0
Jun  36.4
Jul  17.5
Aug  27.5
Sep  60.9
Oct  117.7
Nov  111.0
Dec  97.9
Year 792.9

How do we read such a file?

Reading a mixture of text and numbers

The key idea to process each line is to split the line into words:

months = []
values = []
for line in infile:
    words = line.split()  # split into words
    if words[0] != 'Year':
        months.append(words[0])
        values.append(float(words[1]))

Can split with respect to any string s: line.split(s)

>>> line = 'Oct  117.7'
>>> words = line.split()
>>> words
['Oct', '117.7,']
>>> type(words[1])   # string, not a number!
<type 'str'>

Complete program for reading rainfall data

def extract_data(filename):
    infile = open(filename, 'r')
    infile.readline() # skip the first line
    months = []
    rainfall = []
    for line in infile:
        words = line.split()
        # words[0]: month, words[1]: rainfall
        months.append(words[0])
        rainfall.append(float(words[1]))
    infile.close()
    months = months[:-1]      # Drop the "Year" entry
    annual_avg = rainfall[-1] # Store the annual average
    rainfall = rainfall[:-1]  # Redefine to contain monthly data
    return months, rainfall, annual_avg

months, values, avg = extract_data('rainfall.dat')
print 'The average rainfall for the months:'
for month, value in zip(months, values):
    print month, value
print 'The average rainfall for the year:', avg

Writing data to file

Basic pattern:

outfile = open(filename, 'w')  # 'w' for writing

for data in somelist:
    outfile.write(sometext + '\n')

outfile.close()

Can append text to a file with open(filename, 'a').

Example: Writing a table to file

Problem:

We have a nested list (rows and columns):

data = \
[[ 0.75,        0.29619813, -0.29619813, -0.75      ],
 [ 0.29619813,  0.11697778, -0.11697778, -0.29619813],
 [-0.29619813, -0.11697778,  0.11697778,  0.29619813],
 [-0.75,       -0.29619813,  0.29619813,  0.75      ]]

Write these data to file in tabular form

Solution:

outfile = open('tmp_table.dat', 'w')
for row in data:
    for column in row:
        outfile.write('%14.8f' % column)
    outfile.write('\n')
outfile.close()

Resulting file:

    0.75000000    0.29619813   -0.29619813   -0.75000000
    0.29619813    0.11697778   -0.11697778   -0.29619813
   -0.29619813   -0.11697778    0.11697778    0.29619813
   -0.75000000   -0.29619813    0.29619813    0.75000000

What is a file?

A file is a sequence of characters
For simple text files, each character is one byte (=8 bits, a bit is 0 or 1), which gives $ 2^8=256 $ different characters
(Text files in, e.g., Chinese and Japanese need several bytes for each character)
Save the text "ABCD" to file in Gedit/Emacs and OpenOffice/Word and examine the file!
File reading in Python is about either reading all characters (read) or reading line by line (readline, readlines, for line in fileobj)

Back to a simple program that reads from the command line

Code:

import sys
C = float(sys.argv[1])
F = 5./9*C + 32
print F

Next topic:

How to handle wrong input from the user?

Our program stops with a strange error message if the command-line argument is missing

A user can easily use our program in a wrong way, e.g.,

Terminal> python c2f_cml.py
Traceback (most recent call last):
  File "c2f_cml.py", line 2, in ?
    C = float(sys.argv[1])
IndexError: list index out of range

Why?

The user forgot to provide a command-line argument
sys.argv has then only one element, sys.argv[0], which is the program name (c2f_cml.py)
Index 1, in sys.argv[1], points to a non-existing element in the sys.argv list
Any index corresponding to a non-existing element in a list leads to IndexError

We should handle errors in input!

How can we take control, explain what was wrong with the input, and stop the program without strange Python error messages?

# Program c2f_cml_if.py

import sys
if len(sys.argv) < 2:
    print 'You failed to provide a command-line arg.!'
    sys.exit(1)  # abort
F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)

Terminal> python c2f_cml_if.py
You failed to provide a command-line arg.!

Exceptions as an alternative to if tests

Rather than test if something is wrong, recover from error, else do what we indended to do, it is common in Python (and many other languages) to try to do what we indend to, and if it fails, we recover from the error
This principle makes use of a try-except block

try:
    <statements we intend to do>
except:
    <statements for handling errors>

If something goes wrong in the try block, Python raises an exception and the execution jumps immediately to the except block.

The temperature conversion program with try-except

Try to read C from the command-line, if it fails, tell the user, and abort execution:

import sys
try:
    C = float(sys.argv[1])
except:
    print 'You failed to provide a command-line arg.!'
    sys.exit(1)  # abort
F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)

Execution:

Terminal> python c2f_cml_except1.py
You failed to provide a command-line arg.!

Terminal> python c2f_cml_except1.py 21C
You failed to provide a command-line arg.!

It is good programming style to test for specific exceptions

It is good programming style to test for specific exceptions:

try:
    C = float(sys.argv[1])
except IndexError:
    print 'You failed to provide a command-line arg.!'

If we have an index out of bounds in sys.argv, an IndexError exception is raised, and we jump to the except block.

If any other exception arises, Python aborts the execution:

Terminal> python c2f_cml_tmp.py 21C
Traceback (most recent call last):
  File "tmp.py", line 3, in <module>
    C = float(sys.argv[1])
ValueError: invalid literal for float(): 21C

Improvement: test for IndexError and ValueError exceptions

import sys
try:
    C = float(sys.argv[1])
except IndexError:
    print 'No command-line argument for C!'
    sys.exit(1)  # abort execution
except ValueError:
    print 'C must be a pure number, not "%s"' % sys.argv[1]
    sys.exit(1)

F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)

Executions:

Terminal> python c2f_cml_v3.py
No command-line argument for C!

Terminal> python c2f_cml_v3.py 21C
Celsius degrees must be a pure number, not "21C"

The programmer can raise exceptions

Instead of just letting Python raise exceptions, we can raise our own and tailor the message to the problem at hand
We provide two examples on this:

catching an exception, but raising a new one with an improved (tailored) error message
raising an exception because of wrong input data

Baisc syntax: raise ExceptionType(message)

Examples on re-raising exceptions with better messages

def read_C():
    try:
        C = float(sys.argv[1])
    except IndexError:
        # re-raise, but with specific explanation:
        raise IndexError(
          'Celsius degrees must be supplied on the command line')
    except ValueError:
        # re-raise, but with specific explanation:
        raise ValueError(
         'Degrees must be number, not "%s"' % sys.argv[1])

    # C is read correctly as a number, but can have wrong value:
    if C < -273.15:
        raise ValueError('C=%g is a non-physical value!' % C)
    return C

Calling the previous function and running the program

try:
    C = read_C()
except (IndexError, ValueError) as e:
    # print exception message and stop the program
    print e
    sys.exit(1)

Executions:

Terminal> c2f_cml.py
Celsius degrees must be supplied on the command line

Terminal> c2f_cml.py 21C
Celsius degrees must be a pure number, not "21C"

Terminal> c2f_cml.py -500
C=-500 is a non-physical value!

Terminal> c2f_cml.py 21
21C is 69.8F

Making your own modules

We have frequently used modules like math and sys:

from math import log
r = log(6)   # call log function in math module

import sys
x = eval(sys.argv[1])  # access list argv in sys module

Characteristics of modules:

Collection of useful data and functions
(later also classes)
Functions in a module can be reused in many different programs
If you have some general functions that can be handy in more than one program, make a module with these functions
It's easy: just collect the functions you want in a file, and that's a module!

Case on making our own module

Here are formulas for computing with interest rates: $$ \begin{align} A &= A_0\left( 1 + {p\over 360\cdot 100}\right)^{n}, \label{input:mod:eq1}\\ A_0 &= A\left( 1 + {p\over 360\cdot 100}\right)^{-n}, \label{input:mod:eq2}\\ n &= \frac{\ln {A\over A_0}}{\ln \left( 1 + {p\over 360\cdot 100}\right)} , \label{input:mod:eq3}\\ p &= 360\cdot 100 \left(\left({A\over A_0}\right)^{1/n} - 1\right)\tp \label{input:mod:eq4} \end{align} $$ $ A_0 $: initial amount, $ p $: percentage, $ n $: days, $ A $: final amount

We want to make a module with these four functions.

First we make Python functions for the formuluas

from math import log as ln

def present_amount(A0, p, n):
    return A0*(1 + p/(360.0*100))**n

def initial_amount(A, p, n):
    return A*(1 + p/(360.0*100))**(-n)

def days(A0, A, p):
    return ln(A/A0)/ln(1 + p/(360.0*100))

def annual_rate(A0, A, n):
    return 360*100*((A/A0)**(1.0/n) - 1)

Then we can make the module file

Collect the 4 functions in a file interest.py
Now interest.py is actually a module interest (!)

Example on use:

# How long time does it take to double an amount of money?

from interest import days
A0 = 1; A = 2; p = 5
n = days(A0, 2, p)
years = n/365.0
print 'Money has doubled after %.1f years' % years

Adding a test block in a module file

Module files can have an if test at the end containing a test block for testing or demonstrating the module
The test block is not executed when the file is imported as a module in another program
The test block is executed only when the file is run as a program

if __name__ == '__main__': # this test defineds the test block
    <block of statements>

In our case:

if __name__ == '__main__':
    A = 2.2133983053266699
    A0 = 2.0
    p = 5
    n = 730
    print 'A=%g (%g) A0=%g (%.1f) n=%d (%d) p=%g (%.1f)' % \
          (present_amount(A0, p, n), A,
           initial_amount(A, p, n), A0,
           days(A0, A, p), n,
           annual_rate(A0, A, n), p)

Test blocks are often collected in functions

Let's make a real test function for what we had in the test block:

def test_all_functions():
    # Define compatible values
    A = 2.2133983053266699; A0 = 2.0; p = 5; n = 730
    # Given three of these, compute the remaining one
    # and compare with the correct value (in parenthesis)
    A_computed = present_amount(A0, p, n)
    A0_computed = initial_amount(A, p, n)
    n_computed = days(A0, A, p)
    p_computed = annual_rate(A0, A, n)
    def float_eq(a, b, tolerance=1E-12):
        """Return True if a == b within the tolerance."""
        return abs(a - b) < tolerance

    success = float_eq(A_computed,  A)  and \
              float_eq(A0_computed, A0) and \
              float_eq(p_computed,  p)  and \
              float_eq(n_computed,  n)
    assert success  # could add message here if desired

if __name__ == '__main__':
    test_all_functions()

How can Python find our new module?

If the module is in the same folder as the main program, everything is simple and ok
Home-made modules are normally collected in a common folder, say /Users/hpl/lib/python/mymods
In that case Python must be notified that our module is in that folder

Technique 1: add folder to PYTHONPATH in .bashrc:

export PYTHONPATH=$PYTHONPATH:/Users/hpl/lib/python/mymods

Technique 2: add folder to sys.path in the program:

sys.path.insert(0, '/Users/hpl/lib/python/mymods')

Technique 3: move the module file in a directory that Python already searches for libraries.

Summary of reading from the keyboard and command line

Question and answer input:

var = raw_input('Give value: ')   # var is string!

# if var needs to be a number:
var = float(var)
# or in general:
var = eval(var)

Command-line input:

import sys
parameter1 = eval(sys.argv[1])
parameter3 = sys.argv[3]          # string is ok
parameter2 = eval(sys.argv[2])

Recall: sys.argv[0] is the program name

Summary of reading options-value pairs

--option value pairs with the aid of argparse:

import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--p1', '--parameter_1', type=float,
                    default=0.0, help='1st parameter')
parser.add_argument('--p2', type=float,
                    default=0.0, help='2nd parameter')

args = parser.parse_args()
p1 = args.p1
p2 = args.p2

On the command line we can provide any or all of these options:

Terminal> program prog.py --parameter_1 2.1 --p2 -9

Summary of eval and exec

Evaluating string expressions with eval:

>>> x = 20
>>> r = eval('x + 1.1')
>>> r
21.1
>>> type(r)
<type 'float'>

Executing strings with Python code, using exec:

exec("""
def f(x):
    return %s
""" % sys.argv[1])

Summary of exceptions

Handling exceptions:

try:
    <statements>
except ExceptionType1:
    <provide a remedy for ExceptionType1 errors>
except ExceptionType2, ExceptionType3, ExceptionType4:
    <provide a remedy for three other types of errors>
except:
    <provide a remedy for any other errors>
...

Raising exceptions:

if z < 0:
    raise ValueError(
        'z=%s is negative - cannot do log(z)' % z)

Summary of file reading and writing

infile  = open(filename, 'r')   # read
outfile = open(filename, 'w')   # write
outfile = open(filename, 'a')   # append

# Reading
line    = infile.readline()   # read the next line
filestr = infile.read()       # read rest of file into string
lines   = infile.readlines()  # read rest of file into list
for line in infile:           # read rest of file line by line

# Writing
outfile.write(s)   # add \n if you need it

# Closing
infile.close()
outfile.close()

A summarizing example: solving $ f(x)=0 $

Nonlinear algebraic equations like $$ \begin{align*} x &= 1 + \sin x\\ \tan x + \cos x &= \sin 8x\\ x^5 - 3x^3 &= 10 \end{align*} $$ are usually impossible to solve by pen and paper, but can be solved by numerical methods. To this end, rewrite any equation as $$ f(x) = 0 $$ For the above we have (put everything on the left-hand side) $$ \begin{align*} f(x) &= x - 1 - \sin x\\ f(x) &= \tan x + \cos x - \sin 8x\\\ f(x) &= x^5 - 3x^3 - 10 \end{align*} $$

We shall learn about a method for solving $ f(x)=0 $

A solution $ x $ of $ f(x)=0 $ is called a root of $ f(x) $

Outline of the next slides:

Formulate a method for finding a root
Translate the method to a precise algorithm
Implement the algorithm in Python
Test the implementation

The Bisection method

Start with an interval $ [a,b] $ in which $ f(x) $ changes sign
Then there must be (at least) one root in $ [a,b] $
Halve the interval:

$ m=(a+b)/2 $; does $ f $ change sign in left half $ [a,m] $?
Yes: continue with left interval $ [a,m] $ (set $ b=m $)
No: continue with right interval $ [m,b] $ (set $ a=m $)

Repeat the procedure

After halving the initial interval $ [p,q] $ $n$ times, we know that $ f(x) $ must have a root inside a (small) interval $ 2^{-n}(q-p) $
The method is slow, but very safe
Other methods (like Newton's method) can be faster, but may also fail to locate a root - bisection does not fail

Solving $ \cos \pi x =0 $: iteration no. 1

Solving $ \cos \pi x =0 $: iteration no. 2

Solving $ \cos \pi x =0 $: iteration no. 3

Solving $ \cos \pi x =0 $: iteration no. 4

From method description to a precise algorithm

We need to translate the mathematical description of the Bisection method to a Python program
An important intermediate step is to formulate a precise algorithm
Algorithm = detailed, code-like formulation of the method

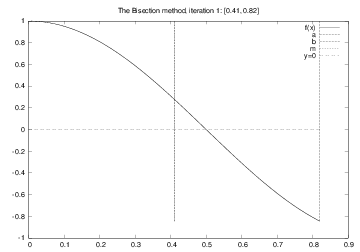
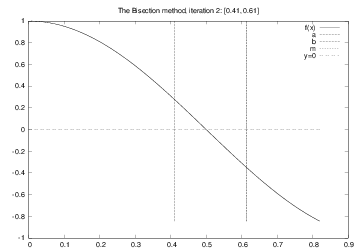
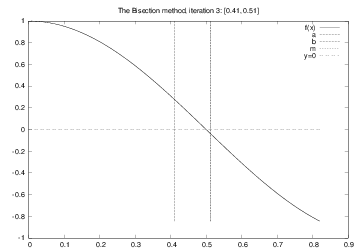
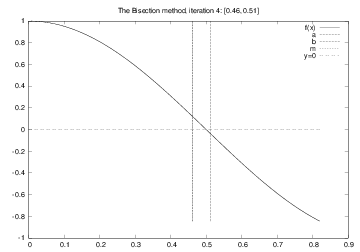
for i in range(0, n+1):
    m = (a + b)/2
    if f(a)*f(m) <= 0:
        b = m  # root is in left half
    else:
        a = m  # root is in right half

# f(x) has a root in [a,b]

The algorithm can be made more efficient

$ f(a) $ is recomputed in each if test
This is not necessary if $ a $ has not changed since last pass in the loop
On modern computers and simple formulas for $ f(x) $ these extra computations do not matter
However, in science and engineering one meets $ f $ functions that take hours or days to evaluate at a point, and saving some $ f(a) $ evaluations matters!
Rule of thumb: remove redundant computations
(unless the code becomes much more complicated, and harder to verify)

New, more efficient version of the algorithm

Idea: save $ f(x) $ evaluations in variables

f_a = f(a)
for i in range(0, n+1):
    m = (a + b)/2
    f_m = f(m)
    if f_a*f_m <= 0:
        b = m   # root is in left half
    else:
        a = m   # root is in right half
        f_a = f_m

# f(x) has a root in [a,b]

How to choose $ n $? That is, when to stop the iteration

We want the error in the root to be $ \epsilon $ or smaller
After $ n $ iterations, the initial interval $ [a,b] $ is halved $ n $ times and the current interval has length $ 2^{-n}(b-a) $. This is sufficiently small if $ 2^{-n}(b-a) = \epsilon \quad\Rightarrow\quad n = - {\ln\epsilon -\ln (b-a)\over\ln 2} $
A simpler alternative: just repeat halving until the length of the current interval is $ \leq\epsilon $
This is easiest done with a while loop:
while b-a <= epsilon:
We also add a test to check if $ f $ really changes sign in the initial inverval $ [a,b] $

Final version of the Bisection algorithm

f_a=f(a)
if f_a*f(b) > 0:
    # error: f does not change sign in [a,b]

i = 0
while b-a > epsilon:
    i = i + 1
    m = (a + b)/2
    f_m = f(m)
    if f_a*f_m <= 0:
        b = m  # root is in left half
    else:
        a = m  # root is in right half
        f_a = f_m

# if x is the real root, |x-m| < epsilon

Python implementation of the Bisection algorithm

def f(x):
    return 2*x - 3   # one root x=1.5

eps = 1E-5
a, b = 0, 10

fa = f(a)
if fa*f(b) > 0:
    print 'f(x) does not change sign in [%g,%g].' % (a, b)
    sys.exit(1)

i = 0   # iteration counter
while b-a > eps:
    i += 1
    m = (a + b)/2.0
    fm = f(m)
    if fa*fm <= 0:
        b = m  # root is in left half of [a,b]
    else:
        a = m  # root is in right half of [a,b]
        fa = fm
x = m          # this is the approximate root

Implementation as a function (more reusable!)

def bisection(f, a, b, eps):
    fa = f(a)
    if fa*f(b) > 0:
        return None, 0
        # Alternative: raise ValueError(
        # 'No change of sign in [%g,%g]' % (a, b))

    i = 0   # iteration counter
    while b-a > eps:
        i += 1
        m = (a + b)/2.0
        fm = f(m)
        if fa*fm <= 0:
            b = m   # root is in left  half of [a,b]
        else:
            a = m   # root is in right half of [a,b]
            fa = fm
    return m, i

print bisection(f=lambda x: 2*x-3, a=0, b=10, eps=1E-5)

Make a module of this function

If we put the bisection function in a file bisection.py, we automatically have a module, and the bisection function can easily be imported in other programs to solve $ f(x)=0 $
We should make a test function too

def test_bisection():
    def f(x):
        return 2*x - 3   # only one root x=1.5

    eps = 1E-5
    x, iter = bisection(f, a=0, b=10, eps=eps)
    success = abs(x - 1.5) < eps  # test within eps tolerance
    assert success, 'found x=%g != 1.5' % x

if __name__ == '__main__':
    test_bisection()

To the point of this lecture: get input!

We want to provide an $ f(x) $ formula at the command line along with $ a $ and $ b $ (3 command-line args)

Usage:

Terminal> python bisection.py 'sin(pi*x**3)-x**2' -1 3.5

Reading input:

def get_input():
    """Get f, a, b, eps from the command line."""
    from scitools.std import StringFunction
    f = StringFunction(sys.argv[1])
    a = float(sys.argv[2])
    b = float(sys.argv[3])
    eps = float(sys.argv[4])
    return f, a, b, eps

# Usage:
f, a, b, eps = get_input()
x, iter = bisection(f, a, b, eps)
print 'Found root x=%g in %d iterations' % (x, iter)

Improvements: error handling

def get_input():
    """Get f, a, b, eps from the command line."""
    from scitools.std import StringFunction
    try:
        f = StringFunction(sys.argv[1])
        a = float(sys.argv[2])
        b = float(sys.argv[3])
        eps = float(sys.argv[4])
    except IndexError:
        print 'Usage %s: f a b eps' % sys.argv[0]
        sys.exit(1)
    return f, a, b, eps

Applications of the Bisection method

Two examples: $ \tanh x = x $ and $ \tanh x^5 = x^5 $:

Terminal> python bisection_plot.py "x-tanh(x)" -1 1
Terminal> python bisection_plot.py "x**5-tanh(x**5)" -1 1

The first equation is easy to treat, but the second leads to much less accurate results. Why??