Ch.7: Introduction to classes

Hans Petter Langtangen [1, 2]

 

[1] Simula Research Laboratory
[2] University of Oslo, Dept. of Informatics

 

Aug 15, 2015


Basics of classes

Class = functions + data (variables) in one unit

  • A class packs together data (a collection of variables) and functions as one single unit

  • As a programmer you can create a new class and thereby a new object type (like float, list, file, ...)

  • A class is much like a module: a collection of "global" variables and functions that belong together

  • There is only one instance of a module while a class can have many instances (copies)

  • Modern programming applies classes to a large extent

  • It will take some time to master the class concept

  • Let's learn by doing!

Representing a function by a class; background

Consider a function of \( t \) with a parameter \( v_0 \):

 
$$ y(t; v_0)=v_0t - {1\over2}gt^2$$

 

We need both \( v_0 \) and \( t \) to evaluate \( y \) (and \( g=9.81 \)), but how should we implement this?

Having \( t \) and \( v_0 \) as arguments: 

def y(t, v0):
    g = 9.81
    return v0*t - 0.5*g*t**2

Having \( t \) as argument and \( v_0 \) as global variable: 

def y(t):
    g = 9.81
    return v0*t - 0.5*g*t**2

Motivation: \( y(t) \) is a function of \( t \) only

Representing a function by a class; idea

  • With a class, y(t) can be a function of t only, but still have

v0 and g as parameters with given values.

  • The class packs together a function y(t) and data (v0, g)

Representing a function by a class; technical overview

  • We make a class Y for \( y(t;v_0) \) with variables v0 and g and a function value(t) for computing \( y(t;v_0) \)

  • Any class should also have a function __init__ for initialization of the variables

Representing a function by a class; the code 

class Y:
    def __init__(self, v0):
        self.v0 = v0
        self.g = 9.81

    def value(self, t):
        return self.v0*t - 0.5*self.g*t**2

Usage: 

y = Y(v0=3)            # create instance (object)
v = y.value(0.1)       # compute function value

Representing a function by a class; the constructor

When we write 

y = Y(v0=3)

we create a new variable (instance) y of type Y. Y(3) is a call to the constructor: 

    def __init__(self, v0):
        self.v0 = v0
        self.g = 9.81

What is this self variable? Stay cool - it will be understood later as you get used to it

  • Think of self as y, i.e., the new variable to be created. self.v0 = ... means that we attach a variable v0 to self (y).

  • Y(3) means Y.__init__(y, 3), i.e., set self=y, v0=3

  • Remember: self is always first parameter in a function, but never inserted in the call!

  • After y = Y(3), y has two variables v0 and g

print y.v0
print y.g

In mathematics you don't understand things. You just get used to them. John von Neumann, mathematician, 1903-1957.

Representing a function by a class; the value method

  • Functions in classes are called methods

  • Variables in classes are called attributes

Here is the value method: 

def value(self, t):
    return self.v0*t - 0.5*self.g*t**2

Example on a call: 

v = y.value(t=0.1)

self is left out in the call, but Python automatically inserts y as the self argument inside the value method. Think of the call as 

Y.value(y, t=0.1)

Inside value things "appear" as 

return y.v0*t - 0.5*y.g*t**2

self gives access to "global variables" in the class object.

Representing a function by a class; summary

  • Class Y collects the attributes v0 and g and the method value as one unit

  • value(t) is function of t only, but has automatically access to the parameters v0 and g as self.v0 and self.g

  • The great advantage: we can send y.value as an ordinary function of t to any other function that expects a function f(t) of one variable

def make_table(f, tstop, n):
    for t in linspace(0, tstop, n):
        print t, f(t)

def g(t):
    return sin(t)*exp(-t)

table(g, 2*pi, 101)         # send ordinary function

y = Y(6.5)
table(y.value, 2*pi, 101)   # send class method

Representing a function by a class; the general case

Given a function with \( n+1 \) parameters and one independent variable,

 
$$ f(x; p_0,\ldots,p_n)$$

 
it is wise to represent f by a class where \( p_0,\ldots,p_n \) are attributes and where there is a method, say value(self, x), for computing \( f(x) \) 

class MyFunc:
    def __init__(self, p0, p1, p2, ..., pn):
        self.p0 = p0
        self.p1 = p1
        ...
        self.pn = pn

    def value(self, x):
        return ...

Class for a function with four parameters

 
$$ v(r; \beta, \mu_0, n, R) = \left({\beta\over 2\mu_0}\right)^{{1\over n}} {n \over n+1}\left( R^{1 + {1\over n}} - r^{1 + {1\over n}}\right) $$

 

class VelocityProfile:
    def __init__(self, beta, mu0, n, R):
        self.beta, self.mu0, self.n, self.R = \
        beta, mu0, n, R

    def value(self, r):
        beta, mu0, n, R = \
        self.beta, self.mu0, self.n, self.R
        n = float(n)  # ensure float divisions
        v = (beta/(2.0*mu0))**(1/n)*(n/(n+1))*\
            (R**(1+1/n) - r**(1+1/n))
        return v

v = VelocityProfile(R=1, beta=0.06, mu0=0.02, n=0.1)
print v.value(r=0.1)

Rough sketch of a general Python class 

class MyClass:
    def __init__(self, p1, p2):
        self.attr1 = p1
        self.attr2 = p2

    def method1(self, arg):
        # can init new attribute outside constructor:
        self.attr3 = arg
        return self.attr1 + self.attr2 + self.attr3

    def method2(self):
        print 'Hello!'

m = MyClass(4, 10)
print m.method1(-2)
m.method2()

It is common to have a constructor where attributes are initialized, but this is not a requirement - attributes can be defined whenever desired

You can learn about other versions and views of class Y in the course book

  • The book features a section on a different version of class Y where there is no constructor (which is possible)

  • The book also features a section on how to implement classes without using classes

  • These sections may be clarifying - or confusing

But what is this self variable? I want to know now!

Warning.

You have two choices:

  1. follow the detailed explanations of what self really is

  2. postpone understanding self until you have much more experience with class programming (suddenly self becomes clear!)

The syntax 

y = Y(3)

can be thought of as 

Y.__init__(y, 3)   # class prefix Y. is like a module prefix

Then 

self.v0 = v0

is actually 

y.v0 = 3

How self works in the value method 

v = y.value(2)

can alternatively be written as 

v = Y.value(y, 2)

So, when we do instance.method(arg1, arg2), self becomes instance inside method.

Working with multiple instances may help explain self

id(obj): print unique Python identifier of an object 

class SelfExplorer:
    """Class for computing a*x."""
    def __init__(self, a):
        self.a = a
        print 'init: a=%g, id(self)=%d' % (self.a, id(self))

    def value(self, x):
        print 'value: a=%g, id(self)=%d' % (self.a, id(self))
        return self.a*x


>>> s1 = SelfExplorer(1)
init: a=1, id(self)=38085696
>>> id(s1)
38085696

>>> s2 = SelfExplorer(2)
init: a=2, id(self)=38085192
>>> id(s2)
38085192

>>> s1.value(4)
value: a=1, id(self)=38085696
4
>>> SelfExplorer.value(s1, 4)
value: a=1, id(self)=38085696
4

>>> s2.value(5)
value: a=2, id(self)=38085192
10
>>> SelfExplorer.value(s2, 5)
value: a=2, id(self)=38085192
10

But what is this self variable? I want to know now!

Warning.

You have two choices:

  1. follow the detailed explanations of what self really is

  2. postpone understanding self until you have much more experience with class programming (suddenly self becomes clear!)

The syntax 

y = Y(3)

can be thought of as 

Y.__init__(y, 3)   # class prefix Y. is like a module prefix

Then 

self.v0 = v0

is actually 

y.v0 = 3

How self works in the value method 

v = y.value(2)

can alternatively be written as 

v = Y.value(y, 2)

So, when we do instance.method(arg1, arg2), self becomes instance inside method.

Working with multiple instances may help explain self

id(obj): print unique Python identifier of an object 

class SelfExplorer:
    """Class for computing a*x."""
    def __init__(self, a):
        self.a = a
        print 'init: a=%g, id(self)=%d' % (self.a, id(self))

    def value(self, x):
        print 'value: a=%g, id(self)=%d' % (self.a, id(self))
        return self.a*x


>>> s1 = SelfExplorer(1)
init: a=1, id(self)=38085696
>>> id(s1)
38085696

>>> s2 = SelfExplorer(2)
init: a=2, id(self)=38085192
>>> id(s2)
38085192

>>> s1.value(4)
value: a=1, id(self)=38085696
4
>>> SelfExplorer.value(s1, 4)
value: a=1, id(self)=38085696
4

>>> s2.value(5)
value: a=2, id(self)=38085192
10
>>> SelfExplorer.value(s2, 5)
value: a=2, id(self)=38085192
10

Another class example: a bank account

  • Attributes: name of owner, account number, balance

  • Methods: deposit, withdraw, pretty print

class Account:
    def __init__(self, name, account_number, initial_amount):
        self.name = name
        self.no = account_number
        self.balance = initial_amount

    def deposit(self, amount):
        self.balance += amount

    def withdraw(self, amount):
        self.balance -= amount

    def dump(self):
        s = '%s, %s, balance: %s' % \
            (self.name, self.no, self.balance)
        print s

UML diagram of class Account

Example on using class Account 

>>> a1 = Account('John Olsson', '19371554951', 20000)
>>> a2 = Account('Liz Olsson',  '19371564761', 20000)
>>> a1.deposit(1000)
>>> a1.withdraw(4000)
>>> a2.withdraw(10500)
>>> a1.withdraw(3500)
>>> print "a1's balance:", a1.balance
a1's balance: 13500
>>> a1.dump()
John Olsson, 19371554951, balance: 13500
>>> a2.dump()
Liz Olsson, 19371564761, balance: 9500

Use underscore in attribute names to avoid misuse

Possible, but not intended use: 

>>> a1.name = 'Some other name'
>>> a1.balance = 100000
>>> a1.no = '19371564768'

The assumptions on correct usage:

  • The attributes should not be changed!

  • The balance attribute can be viewed

  • Changing balance is done through withdraw or deposit

Remedy:

Attributes and methods not intended for use outside the class can be marked as protected by prefixing the name with an underscore (e.g., _name). This is just a convention - and no technical way of avoiding attributes and methods to be accessed.

Improved class with attribute protection (underscore) 

class AccountP:
    def __init__(self, name, account_number, initial_amount):
        self._name = name
        self._no = account_number
        self._balance = initial_amount

    def deposit(self, amount):
        self._balance += amount

    def withdraw(self, amount):
        self._balance -= amount

    def get_balance(self):    # NEW - read balance value
        return self._balance

    def dump(self):
        s = '%s, %s, balance: %s' % \
            (self._name, self._no, self._balance)
        print s

Usage of improved class AccountP 

a1 = AccountP('John Olsson', '19371554951', 20000)
a1.withdraw(4000)

print a1._balance      # it works, but a convention is broken

print a1.get_balance() # correct way of viewing the balance

a1._no = '19371554955' # this is a "serious crime"!

Another example: a phone book

  • A phone book is a list of data about persons

  • Data about a person: name, mobile phone, office phone, private phone, email

  • Let us create a class for data about a person!

  • Methods:

    • Constructor for initializing name, plus one or more other data

    • Add new mobile number

    • Add new office number

    • Add new private number

    • Add new email

    • Write out person data

UML diagram of class Person

Basic code of class Person 

 class Person:
    def __init__(self, name,
                 mobile_phone=None, office_phone=None,
                 private_phone=None, email=None):
        self.name = name
        self.mobile = mobile_phone
        self.office = office_phone
        self.private = private_phone
        self.email = email

    def add_mobile_phone(self, number):
        self.mobile = number

    def add_office_phone(self, number):
        self.office = number

    def add_private_phone(self, number):
        self.private = number

    def add_email(self, address):
        self.email = address

Code of a dump method for printing all class contents 

 class Person:
    ...
    def dump(self):
        s = self.name + '\n'
        if self.mobile is not None:
            s += 'mobile phone:   %s\n' % self.mobile
        if self.office is not None:
            s += 'office phone:   %s\n' % self.office
        if self.private is not None:
            s += 'private phone:  %s\n' % self.private
        if self.email is not None:
            s += 'email address:  %s\n' % self.email
        print s

Usage: 

p1 = Person('Hans Petter Langtangen', email='hpl@simula.no')
p1.add_office_phone('67828283'),
p2 = Person('Aslak Tveito', office_phone='67828282')
p2.add_email('aslak@simula.no')
phone_book = [p1, p2]                           # list
phone_book = {'Langtangen': p1, 'Tveito': p2}   # better
for p in phone_book:
    p.dump()

Another example: a class for a circle

  • A circle is defined by its center point \( x_0 \), \( y_0 \) and its radius \( R \)

  • These data can be attributes in a class

  • Possible methods in the class: area, circumference

  • The constructor initializes \( x_0 \), \( y_0 \) and \( R \)

class Circle:
    def __init__(self, x0, y0, R):
        self.x0, self.y0, self.R = x0, y0, R

    def area(self):
        return pi*self.R**2

    def circumference(self):
        return 2*pi*self.R


>>> c = Circle(2, -1, 5)
>>> print 'A circle with radius %g at (%g, %g) has area %g' % \
...       (c.R, c.x0, c.y0, c.area())
A circle with radius 5 at (2, -1) has area 78.5398

Test function for class Circle 

def test_Circle():
    R = 2.5
    c = Circle(7.4, -8.1, R)

    from math import pi
    expected_area = pi*R**2
    computed_area = c.area()
    diff = abs(expected_area - computed_area)
    tol = 1E-14
    assert diff < tol, 'bug in Circle.area, diff=%s' % diff

    expected_circumference = 2*pi*R
    computed_circumference = c.circumference()
    diff = abs(expected_circumference - computed_circumference)
    assert diff < tol, 'bug in Circle.circumference, diff=%s' % diff

Special methods 

class MyClass:
    def __init__(self, a, b):
    ...

p1 = MyClass(2, 5)
p2 = MyClass(-1, 10)

p3 = p1 + p2
p4 = p1 - p2
p5 = p1*p2
p6 = p1**7 + 4*p3

Special methods allow nice syntax and are recognized by double leading and trailing underscores 

def __init__(self, ...)
def __call__(self, ...)
def __add__(self, other)

# Python syntax
y = Y(4)
print y(2)
z = Y(6)
print y + z

# What's actually going on
Y.__init__(y, 4)
print Y.__call__(y, 2)
Y.__init__(z, 6)
print Y.__add__(y, z)

We shall learn about many more such special methods

Example on a call special method

Replace the value method by a call special method: 

class Y:
    def __init__(self, v0):
        self.v0 = v0
        self.g = 9.81

    def __call__(self, t):
        return self.v0*t - 0.5*self.g*t**2

Now we can write 

y = Y(3)
v = y(0.1) # same as v = y.__call__(0.1) or Y.__call__(y, 0.1)

Note:

  • The instance y behaves and looks as a function!

  • The value(t) method does the same, but __call__ allows nicer syntax for computing function values

Representing a function by a class revisited

Given a function with \( n+1 \) parameters and one independent variable,

 
$$ f(x; p_0,\ldots,p_n)$$

 
it is wise to represent f by a class where \( p_0,\ldots,p_n \) are attributes and __call__(x) computes \( f(x) \) 

class MyFunc:
    def __init__(self, p0, p1, p2, ..., pn):
        self.p0 = p0
        self.p1 = p1
        ...
        self.pn = pn

    def __call__(self, x):
        return ...

Can we automatically differentiate a function?

Given some mathematical function in Python, say 

def f(x):
    return x**3

can we make a class Derivative and write 

dfdx = Derivative(f)

so that dfdx behaves as a function that computes the derivative of f(x)? 

print dfdx(2)   # computes 3*x**2 for x=2

Automagic differentiation; solution

Method.

We use numerical differentiation "behind the curtain":

 
$$ f'(x) \approx {f(x+h)-f(x)\over h} $$

 
for a small (yet moderate) \( h \), say \( h=10^{-5} \)

Implementation. 

class Derivative:
    def __init__(self, f, h=1E-5):
        self.f = f
        self.h = float(h)

    def __call__(self, x):
        f, h = self.f, self.h      # make short forms
        return (f(x+h) - f(x))/h

Automagic differentiation; demo 

>>> from math import *
>>> df = Derivative(sin)
>>> x = pi
>>> df(x)
-1.000000082740371
>>> cos(x)  # exact
-1.0
>>> def g(t):
...     return t**3
...
>>> dg = Derivative(g)
>>> t = 1
>>> dg(t)  # compare with 3 (exact)
3.000000248221113

Automagic differentiation; useful in Newton's method

Newton's method solves nonlinear equations \( f(x)=0 \), but the method requires \( f'(x) \) 

def Newton(f, xstart, dfdx, epsilon=1E-6):
    ...
    return x, no_of_iterations, f(x)

Suppose \( f'(x) \) requires boring/lengthy derivation, then class Derivative is handy: 

>>> def f(x):
...     return 100000*(x - 0.9)**2 * (x - 1.1)**3
...
>>> df = Derivative(f)
>>> xstart = 1.01
>>> Newton(f, xstart, df, epsilon=1E-5)
(1.0987610068093443, 8, -7.5139644257961411e-06)

Automagic differentiation; test function

  • How can we test class Derivative?

  • Method 1: compute \( (f(x+h)-f(x))/h \) by hand for some \( f \) and \( h \)

  • Method 2: utilize that linear functions are differentiated exactly by our numerical formula, regardless of \( h \)

Test function based on method 2: 

def test_Derivative():
    # The formula is exact for linear functions, regardless of h
    f = lambda x: a*x + b
    a = 3.5; b = 8
    dfdx = Derivative(f, h=0.5)
    diff = abs(dfdx(4.5) - a)
    assert diff < 1E-14, 'bug in class Derivative, diff=%s' % diff

Automagic differentiation; explanation of the test function

Use of lambda functions: 

f = lambda x: a*x + b

is equivalent to 

def f(x):
    return a*x + b

Lambda functions are convenient for producing quick, short code

Use of closure: 

f = lambda x: a*x + b
a = 3.5; b = 8
dfdx = Derivative(f, h=0.5)
dfdx(4.5)

Looks straightforward...but

  • How can Derivative.__call__ know a and b when it calls our f(x) function?

  • Local functions inside functions remember (have access to) all local variables in the function they are defined (!)

  • f can access a and b in test_Derivative even when called from __call__ in class `Derivative

  • f is known as a closure in computer science

Automagic differentiation detour; sympy solution (exact differentiation via symbolic expressions)

SymPy can perform exact, symbolic differentiation: 

>>> from sympy import *
>>> def g(t):
...     return t**3
...
>>> t = Symbol('t')
>>> dgdt = diff(g(t), t)           # compute g'(t)
>>> dgdt
3*t**2

>>> # Turn sympy expression dgdt into Python function dg(t)
>>> dg = lambdify([t], dgdt)
>>> dg(1)
3

Automagic differentiation detour; class based on sympy 

import sympy as sp

class Derivative_sympy:
    def __init__(self, f):
        # f: Python f(x)
        x = sp.Symbol('x')
        sympy_f = f(x)
        sympy_dfdx = sp.diff(sympy_f, x)
        self.__call__ = sp.lambdify([x], sympy_dfdx)


>>> def g(t):
...    return t**3

>>> def h(y):
...    return sp.sin(y)

>>> dg = Derivative_sympy(g)
>>> dh = Derivative_sympy(h)
>>> dg(1)   # 3*1**2 = 3
3
>>> from math import pi
>>> dh(pi)  # cos(pi) = -1
-1.0

Automagic integration; problem setting

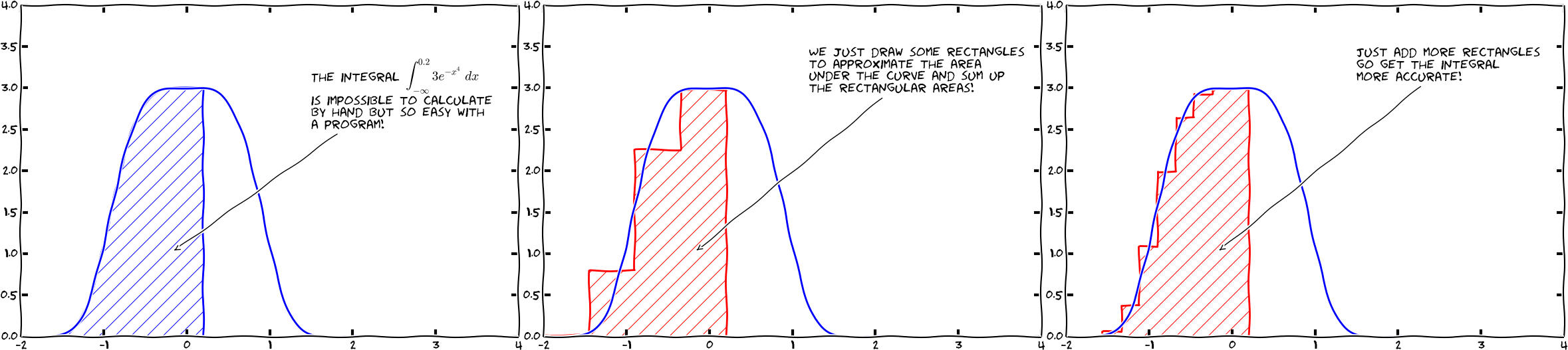
Given a function \( f(x) \), we want to compute

 
$$ F(x; a) = \int_a^x f(t)dt $$

 

Automagic integration; technique

 
$$ F(x; a) = \int_a^x f(t)dt $$

 

Technique: Midpoint rule or Trapezoidal rule, here the latter:

 
$$ \int_a^x f(t)dt = h\left({1\over2}f(a) + \sum_{i=1}^{n-1} f(a+ih) + {1\over2}f(x)\right) $$

 

Desired application code: 

def f(x):
    return exp(-x**2)*sin(10*x)

a = 0; n = 200
F = Integral(f, a, n)
x = 1.2
print F(x)

Automagic integration; implementation 

def trapezoidal(f, a, x, n):
    h = (x-a)/float(n)
    I = 0.5*f(a)
    for i in range(1, n):
        I += f(a + i*h)
    I += 0.5*f(x)
    I *= h
    return I

Class Integral holds f, a and n as attributes and has a call special method for computing the integral: 

class Integral:
    def __init__(self, f, a, n=100):
        self.f, self.a, self.n = f, a, n

    def __call__(self, x):
        return trapezoidal(self.f, self.a, x, self.n)

Automagic integration; test function

  • How can we test class Integral?

  • Method 1: compute by hand for some \( f \) and small \( n \)

  • Method 2: utilize that linear functions are integrated exactly by our numerical formula, regardless of \( n \)

Test function based on method 2: 

def test_Integral():
    f = lambda x: 2*x + 5
    F = lambda x: x**2 + 5*x - (a**2 + 5*a)
    a = 2
    dfdx = Integralf, a, n=4)
    x = 6
    diff = abs(I(x) - (F(x) - F(a)))
    assert diff < 1E-15, 'bug in class Integral, diff=%s' % diff

Special method for printing

  • In Python, we can usually print an object a by print a, works for built-in types (strings, lists, floats, ...)

  • Python does not know how to print objects of a user-defined class, but if the class defines a method __str__, Python will use this method to convert an object to a string

Example: 

class Y:
    ...
    def __call__(self, t):
        return self.v0*t - 0.5*self.g*t**2

    def __str__(self):
        return 'v0*t - 0.5*g*t**2; v0=%g' % self.v0

Demo: 

>>> y = Y(1.5)
>>> y(0.2)
0.1038
>>> print y
v0*t - 0.5*g*t**2; v0=1.5

Class for polynomials; functionality

A polynomial can be specified by a list of its coefficients. For example, \( 1 - x^2 + 2x^3 \) is

 
$$ 1 + 0\cdot x - 1\cdot x^2 + 2\cdot x^3 $$

 

and the coefficients can be stored as [1, 0, -1, 2]

Desired application code: 

>>> p1 = Polynomial([1, -1])
>>> print p1
1 - x
>>> p2 = Polynomial([0, 1, 0, 0, -6, -1])
>>> p3 = p1 + p2
>>> print p3.coeff
[1, 0, 0, 0, -6, -1]
>>> print p3
1 - 6*x^4 - x^5
>>> p2.differentiate()
>>> print p2
1 - 24*x^3 - 5*x^4

How can we make class Polynomial?

Class Polynomial; basic code 

class Polynomial:
    def __init__(self, coefficients):
        self.coeff = coefficients

    def __call__(self, x):
        s = 0
        for i in range(len(self.coeff)):
            s += self.coeff[i]*x**i
        return s

Class Polynomial; addition 

class Polynomial:
    ...

    def __add__(self, other):
        # return self + other

        # start with the longest list and add in the other:
        if len(self.coeff) > len(other.coeff):
            coeffsum = self.coeff[:]  # copy!
            for i in range(len(other.coeff)):
                coeffsum[i] += other.coeff[i]
        else:
            coeffsum = other.coeff[:] # copy!
            for i in range(len(self.coeff)):
                coeffsum[i] += self.coeff[i]
        return Polynomial(coeffsum)

Class Polynomial; multiplication

Mathematics:

Multiplication of two general polynomials:

 
$$ \left(\sum_{i=0}^Mc_ix^i\right)\left(\sum_{j=0}^N d_jx^j\right) = \sum_{i=0}^M \sum_{j=0}^N c_id_j x^{i+j} $$

 

The coeff. corresponding to power \( i+j \) is \( c_i\cdot d_j \). The list r of coefficients of the result: r[i+j] = c[i]*d[j] (i and j running from 0 to \( M \) and \( N \), resp.)

Implementation: 

class Polynomial:
    ...
    def __mul__(self, other):
        M = len(self.coeff) - 1
        N = len(other.coeff) - 1
        coeff = [0]*(M+N+1)  # or zeros(M+N+1)
        for i in range(0, M+1):
            for j in range(0, N+1):
                coeff[i+j] += self.coeff[i]*other.coeff[j]
        return Polynomial(coeff)

Class Polynomial; differentation

Mathematics:

Rule for differentiating a general polynomial:

 
$$ {d\over dx}\sum_{i=0}^n c_ix^i = \sum_{i=1}^n ic_ix^{i-1}$$

 

If c is the list of coefficients, the derivative has a list of coefficients, dc, where dc[i-1] = i*c[i] for i running from 1 to the largest index in c. Note that dc has one element less than c.

Implementation: 

class Polynomial:
    ...
    def differentiate(self):    # change self
        for i in range(1, len(self.coeff)):
            self.coeff[i-1] = i*self.coeff[i]
        del self.coeff[-1]

    def derivative(self):       # return new polynomial
        dpdx = Polynomial(self.coeff[:])  # copy
        dpdx.differentiate()
        return dpdx

Class Polynomial; pretty print 

class Polynomial:
    ...
    def __str__(self):
        s = ''
        for i in range(0, len(self.coeff)):
            if self.coeff[i] != 0:
                s += ' + %g*x^%d' % (self.coeff[i], i)
        # fix layout (lots of special cases):
        s = s.replace('+ -', '- ')
        s = s.replace(' 1*', ' ')
        s = s.replace('x^0', '1')
        s = s.replace('x^1 ', 'x ')
        s = s.replace('x^1', 'x')
        if s[0:3] == ' + ':  # remove initial +
            s = s[3:]
        if s[0:3] == ' - ':  # fix spaces for initial -
            s = '-' + s[3:]
        return s

Class for polynomials; usage

Consider

 
$$ p_1(x)= 1-x,\quad p_2(x)=x - 6x^4 - x^5 $$

 
and their sum

 
$$ p_3(x) = p_1(x) + p_2(x) = 1 -6x^4 - x^5 $$

 

>>> p1 = Polynomial([1, -1])
>>> print p1
1 - x
>>> p2 = Polynomial([0, 1, 0, 0, -6, -1])
>>> p3 = p1 + p2
>>> print p3.coeff
[1, 0, 0, 0, -6, -1]
>>> p2.differentiate()
>>> print p2
1 - 24*x^3 - 5*x^4

The programmer is in charge of defining special methods!

How should, e.g., __add__(self, other) be defined? This is completely up to the programmer, depending on what is meaningful by object1 + object2.

An anthropologist was asking a primitive tribesman about arithmetic. When the anthropologist asked, What does two and two make? the tribesman replied, Five. Asked to explain, the tribesman said, If I have a rope with two knots, and another rope with two knots, and I join the ropes together, then I have five knots.

Special methods for arithmetic operations 

c = a + b    #  c = a.__add__(b)

c = a - b    #  c = a.__sub__(b)

c = a*b      #  c = a.__mul__(b)

c = a/b      #  c = a.__div__(b)

c = a**e     #  c = a.__pow__(e)

Special methods for comparisons 

a == b       #  a.__eq__(b)

a != b       #  a.__ne__(b)

a < b        #  a.__lt__(b)

a <= b       #  a.__le__(b)

a > b        #  a.__gt__(b)

a >= b       #  a.__ge__(b)

Class for vectors in the plane

Mathematical operations for vectors in the plane:

 
$$ \begin{align*} (a,b) + (c,d) &= (a+c, b+d)\\ (a,b) - (c,d) &= (a-c, b-d)\\ (a,b)\cdot(c,d) &= ac + bd\\ (a,b) &= (c, d)\hbox{ if }a=c\hbox{ and }b=d \end{align*} $$

 

Desired application code: 

>>> u = Vec2D(0,1)
>>> v = Vec2D(1,0)
>>> print u + v
(1, 1)
>>> a = u + v
>>> w = Vec2D(1,1)
>>> a == w
True
>>> print u - v
(-1, 1)
>>> print u*v
0

Class for vectors; implementation 

 class Vec2D:
    def __init__(self, x, y):
        self.x = x;  self.y = y

    def __add__(self, other):
        return Vec2D(self.x+other.x, self.y+other.y)

    def __sub__(self, other):
        return Vec2D(self.x-other.x, self.y-other.y)

    def __mul__(self, other):
        return self.x*other.x + self.y*other.y

    def __abs__(self):
        return math.sqrt(self.x**2 + self.y**2)

    def __eq__(self, other):
        return self.x == other.x and self.y == other.y

    def __str__(self):
        return '(%g, %g)' % (self.x, self.y)

    def __ne__(self, other):
        return not self.__eq__(other)  # reuse __eq__

The repr special method: eval(repr(p)) creates p 

class MyClass:
    def __init__(self, a, b):
        self.a, self.b = a, b

    def __str__(self):
        """Return string with pretty print."""
        return 'a=%s, b=%s' % (self.a, self.b)

    def __repr__(self):
        """Return string such that eval(s) recreates self."""
        return 'MyClass(%s, %s)' % (self.a, self.b)


>>> m = MyClass(1, 5)
>>> print m      # calls m.__str__()
a=1, b=5
>>> str(m)       # calls m.__str__()
'a=1, b=5'
>>> s = repr(m)  # calls m.__repr__()
>>> s
'MyClass(1, 5)'
>>> m2 = eval(s) # same as m2 = MyClass(1, 5)
>>> m2           # calls m.__repr__()
'MyClass(1, 5)'

Class Y revisited with repr print method 

class Y:
    """Class for function y(t; v0, g) = v0*t - 0.5*g*t**2."""

    def __init__(self, v0):
        """Store parameters."""
        self.v0 = v0
        self.g = 9.81

    def __call__(self, t):
        """Evaluate function."""
        return self.v0*t - 0.5*self.g*t**2

    def __str__(self):
        """Pretty print."""
        return 'v0*t - 0.5*g*t**2; v0=%g' % self.v0

    def __repr__(self):
        """Print code for regenerating this instance."""
        return 'Y(%s)' % self.v0

Class for complex numbers; functionality

Python already has a class complex for complex numbers, but implementing such a class is a good pedagogical example on class programming (especially with special methods).

Usage: 

>>> u = Complex(2,-1)
>>> v = Complex(1)     # zero imaginary part
>>> w = u + v
>>> print w
(3, -1)
>>> w != u
True
>>> u*v
Complex(2, -1)
>>> u < v
illegal operation "<" for complex numbers
>>> print w + 4
(7, -1)
>>> print 4 - w
(1, 1)

Class for complex numbers; implementation (part 1) 

class Complex:
    def __init__(self, real, imag=0.0):
        self.real = real
        self.imag = imag

    def __add__(self, other):
        return Complex(self.real + other.real,
                       self.imag + other.imag)

    def __sub__(self, other):
        return Complex(self.real - other.real,
                       self.imag - other.imag)

    def __mul__(self, other):
        return Complex(self.real*other.real - self.imag*other.imag,
                       self.imag*other.real + self.real*other.imag)

    def __div__(self, other):
        ar, ai, br, bi = self.real, self.imag, \
                         other.real, other.imag # short forms
        r = float(br**2 + bi**2)
        return Complex((ar*br+ai*bi)/r, (ai*br-ar*bi)/r)

Class for complex numbers; implementation (part 2) 

    def __abs__(self):
        return sqrt(self.real**2 + self.imag**2)

    def __neg__(self):   # defines -c (c is Complex)
        return Complex(-self.real, -self.imag)

    def __eq__(self, other):
        return self.real == other.real and \
               self.imag == other.imag

    def __ne__(self, other):
        return not self.__eq__(other)

    def __str__(self):
        return '(%g, %g)' % (self.real, self.imag)

    def __repr__(self):
        return 'Complex' + str(self)

    def __pow__(self, power):
        raise NotImplementedError(
          'self**power is not yet impl. for Complex')

Refining the special methods for arithmetics

Can we add a real number to a complex number? 

>>> u = Complex(1, 2)
>>> w = u + 4.5
...
AttributeError: 'float' object has no attribute 'real'

Problem: we have assumed that other is Complex. Remedy: 

class Complex:
    ...
    def __add__(self, other):
        if isinstance(other, (float,int)):
            other = Complex(other)
        return Complex(self.real + other.real,
                       self.imag + other.imag)

# or

    def __add__(self, other):
        if isinstance(other, (float,int)):
            return Complex(self.real + other, self.imag)
        else:
            return Complex(self.real + other.real,
                           self.imag + other.imag)

Special methods for "right" operands; addition

What if we try this: 

>>> u = Complex(1, 2)
>>> w = 4.5 + u
...
TypeError: unsupported operand type(s) for +:
    'float' and 'instance'

Problem: Python's float objects cannot add a Complex.

Remedy: if a class has an __radd__(self, other) special method, Python applies this for other + self 

class Complex:
    ...
    def __radd__(self, other):
        """Rturn other + self."""
        # other + self = self + other:
        return self.__add__(other)

Special methods for "right" operands; subtraction

Right operands for subtraction is a bit more complicated since \( a-b \neq b-a \): 

class Complex:
    ...
    def __sub__(self, other):
        if isinstance(other, (float,int)):
            other = Complex(other)
        return Complex(self.real - other.real,
                       self.imag - other.imag)

    def __rsub__(self, other):
        if isinstance(other, (float,int)):
            other = Complex(other)
        return other.__sub__(self)

What's in a class? 

 class A:
    """A class for demo purposes."""
    def __init__(self, value):
        self.v = value

Any instance holds its attributes in the self.__dict__ dictionary (Python automatically creates this dict) 

>>> a = A([1,2])
>>> print a.__dict__  # all attributes
{'v': [1, 2]}
>>> dir(a)            # what's in object a?
'__doc__', '__init__', '__module__', 'dump', 'v']
>>> a.__doc__         # programmer's documentation of A
'A class for demo purposes.'

Ooops - we can add new attributes as we want! 

>>> a.myvar = 10            # add new attribute (!)
>>> a.__dict__
{'myvar': 10, 'v': [1, 2]}
>>> dir(a)
['__doc__', '__init__', '__module__', 'dump', 'myvar', 'v']

>>> b = A(-1)
>>> b.__dict__              # b has no myvar attribute
{'v': -1}
>>> dir(b)
['__doc__', '__init__', '__module__', 'dump', 'v']

Summary of defining a class

Example on a defining a class with attributes and methods: 

class Gravity:
    """Gravity force between two objects."""
    def __init__(self, m, M):
        self.m = m
        self.M = M
        self.G = 6.67428E-11 # gravity constant

    def force(self, r):
        G, m, M = self.G, self.m, self.M
        return G*m*M/r**2

    def visualize(self, r_start, r_stop, n=100):
        from scitools.std import plot, linspace
        r = linspace(r_start, r_stop, n)
        g = self.force(r)
        title='m=%g, M=%g' % (self.m, self.M)
        plot(r, g, title=title)

Summary of using a class

Example on using the class: 

mass_moon = 7.35E+22
mass_earth = 5.97E+24

# make instance of class Gravity:
gravity = Gravity(mass_moon, mass_earth)

r = 3.85E+8  # earth-moon distance in meters
Fg = gravity.force(r)   # call class method

Summary of special methods

  • c = a + b implies c = a.__add__(b)

  • There are special methods for a+b, a-b, a*b, a/b, a**b, -a, if a:, len(a), str(a) (pretty print), repr(a) (recreate a with eval), etc.

  • With special methods we can create new mathematical objects like vectors, polynomials and complex numbers and write "mathematical code" (arithmetics)

  • The call special method is particularly handy: v = c(5) means v = c.__call__(5)

  • Functions with parameters should be represented by a class with the parameters as attributes and with a call special method for evaluating the function

Summarizing example: interval arithmetics for uncertainty quantification in formulas

Uncertainty quantification:

Consider measuring gravity \( g \) by dropping a ball from \( y=y_0 \) to \( y=0 \) in time \( T \):

 
$$ g = 2y_0T^{-2} $$

 

What if \( y_0 \) and \( T \) are uncertain? Say \( y_0\in [0.99,1.01] \) m and \( T\in [0.43, 0.47] \) s. What is the uncertainty in \( g \)?

The uncertainty can be computed by interval arithmetics

Interval arithmetics.

Rules for computing with intervals, \( p=[a,b] \) and \( q=[c,d] \):

  • \( p+q = [a + c, b + d] \)

  • \( p-q = [a - d, b - c] \)

  • \( pq = [\min(ac, ad, bc, bd), \max(ac, ad, bc, bd)] \)

  • \( p/q = [\min(a/c, a/d, b/c, b/d), \max(a/c, a/d, b/c, b/d)] \) (\( [c,d] \) cannot contain zero)

Obvious idea: make a class for interval arithmetics!

Class for interval arithmetics 

class IntervalMath:
    def __init__(self, lower, upper):
        self.lo = float(lower)
        self.up = float(upper)

    def __add__(self, other):
        a, b, c, d = self.lo, self.up, other.lo, other.up
        return IntervalMath(a + c, b + d)

    def __sub__(self, other):
        a, b, c, d = self.lo, self.up, other.lo, other.up
        return IntervalMath(a - d, b - c)

    def __mul__(self, other):
        a, b, c, d = self.lo, self.up, other.lo, other.up
        return IntervalMath(min(a*c, a*d, b*c, b*d),
                            max(a*c, a*d, b*c, b*d))

    def __div__(self, other):
        a, b, c, d = self.lo, self.up, other.lo, other.up
        if c*d <= 0: return None
        return IntervalMath(min(a/c, a/d, b/c, b/d),
                            max(a/c, a/d, b/c, b/d))
    def __str__(self):
        return '[%g, %g]' % (self.lo, self.up)

Demo of the new class for interval arithmetics

Code: 

I = IntervalMath   # abbreviate
a = I(-3,-2)
b = I(4,5)

expr = 'a+b', 'a-b', 'a*b', 'a/b'   # test expressions
for e in expr:
    print e, '=', eval(e)

Output: 

a+b = [1, 3]
a-b = [-8, -6]
a*b = [-15, -8]
a/b = [-0.75, -0.4]

Shortcomings of the class

This code 

a = I(4,5)
q = 2
b = a*q

leads to 

  File "IntervalMath.py", line 15, in __mul__
    a, b, c, d = self.lo, self.up, other.lo, other.up
AttributeError: 'float' object has no attribute 'lo'

Problem: IntervalMath times int is not defined.

Remedy: (cf. class Complex) 

class IntervalArithmetics:
    ...
    def __mul__(self, other):
        if isinstance(other, (int, float)):      # NEW
            other = IntervalMath(other, other)   # NEW
        a, b, c, d = self.lo, self.up, other.lo, other.up
        return IntervalMath(min(a*c, a*d, b*c, b*d),
                            max(a*c, a*d, b*c, b*d))

(with similar adjustments of other special methods)

More shortcomings of the class

Try to compute g = 2*y0*T**(-2): multiplication of int (2) and IntervalMath (y0), and power operation T**(-2) are not defined 

class IntervalArithmetics:
    ...
    def __rmul__(self, other):
        if isinstance(other, (int, float)):
            other = IntervalMath(other, other)
        return other*self

    def __pow__(self, exponent):
        if isinstance(exponent, int):
            p = 1
            if exponent > 0:
                for i in range(exponent):
                    p = p*self
            elif exponent < 0:
                for i in range(-exponent):
                    p = p*self
                p = 1/p
            else:   # exponent == 0
                p = IntervalMath(1, 1)
            return p
        else:
            raise TypeError('exponent must int')

Adding more functionality to the class: rounding

"Rounding" to the midpoint value: 

>>> a = IntervalMath(5,7)
>>> float(a)
6

is achieved by 

class IntervalArithmetics:
    ...
    def __float__(self):
        return 0.5*(self.lo + self.up)

Adding more functionality to the class: repr and str methods 

class IntervalArithmetics:
    ...
    def __str__(self):
        return '[%g, %g]' % (self.lo, self.up)

    def __repr__(self):
        return '%s(%g, %g)' % \
          (self.__class__.__name__, self.lo, self.up)

Demonstrating the class: \( g=2y_0T^{-2} \) 

>>> g = 9.81
>>> y_0 = I(0.99, 1.01)
>>> Tm = 0.45                 # mean T
>>> T = I(Tm*0.95, Tm*1.05)   # 10% uncertainty
>>> print T
[0.4275, 0.4725]
>>> g = 2*y_0*T**(-2)
>>> g
IntervalMath(8.86873, 11.053)
>>> # computing with mean values:
>>> T = float(T)
>>> y = 1
>>> g = 2*y_0*T**(-2)
>>> print '%.2f' % g
9.88

Demonstrating the class: volume of a sphere 

>>> R = I(6*0.9, 6*1.1)   # 20 % error
>>> V = (4./3)*pi*R**3
>>> V
IntervalMath(659.584, 1204.26)
>>> print V
[659.584, 1204.26]
>>> print float(V)
931.922044761
>>> # compute with mean values:
>>> R = float(R)
>>> V = (4./3)*pi*R**3
>>> print V
904.778684234

20% uncertainty in \( R \) gives almost 60% uncertainty in \( V \)