When finding the derivative \( f'(x) \) in Newton's method is problematic, or when function evaluations take too long; we may adjust the method slightly. Instead of using tangent lines to the graph we may use secants. The approach is referred to as the secant method, and the idea is illustrated graphically in Figure 63 for our example problem \( x^2 - 9 = 0 \).
Figure 63: Illustrates the use of secants in the secant method when solving \( x^2 - 9 = 0, x \in [0, 1000] \). From two chosen starting values, \( x_0 = 1000 \) and \( x_1 = 700 \) the crossing \( x_2 \) of the corresponding secant with the \( x \) axis is computed, followed by a similar computation of \( x_3 \) from \( x_1 \) and \( x_2 \).
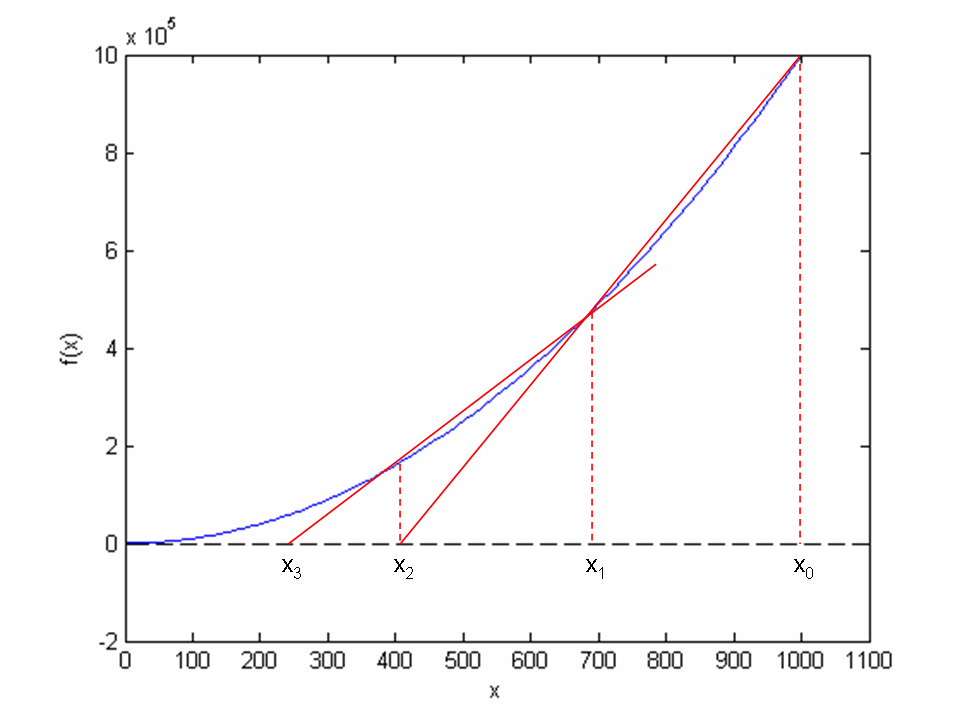
The idea of the secant method is to think as in Newton's method, but instead of using \( f'(x_n) \), we approximate this derivative by a finite difference or the secant, i.e., the slope of the straight line that goes through the two most recent approximations \( x_n \) and \( x_{n-1} \). This slope reads $$ \begin{equation} \frac{f(x_n)-f(x_{n-1})}{x_n - x_{n-1}}\thinspace . \tag{163} \end{equation} $$ Inserting this expression for \( f'(x_n) \) in Newton's method simply gives us the secant method: $$ x_{n+1} = x_n - \frac{f(x_n)}{\frac{f(x_n)-f(x_{n-1})}{x_n - x_{n-1}}},$$ or $$ \begin{equation} x_{n+1} = x_n - f(x_n) \frac{x_n - x_{n-1}}{f(x_n)-f(x_{n-1})} \thinspace . \tag{164} \end{equation} $$ Comparing (164) to the graph in Figure 63, we see how two chosen starting points (\( x_0 = 1000 \), \( x_1= 700 \), and corresponding function values) are used to compute \( x_2 \). Once we have \( x_2 \), we similarly use \( x_1 \) and \( x_2 \) to compute \( x_3 \). As with Newton's method, the procedure is repeated until \( f(x_n) \) is below some chosen limit value, or some limit on the number of iterations has been reached. We use an iteration counter here too, based on the same thinking as in the implementation of Newton's method.
We can store the approximations \( x_n \) in an array, but as in Newton's
method, we notice that the computation of \( x_{n+1} \) only needs
knowledge of \( x_n \) and \( x_{n-1} \), not "older"
approximations. Therefore, we can make use of only three variables:
x for \( x_{n+1} \), x1 for \( x_n \), and x0 for \( x_{n-1} \). Note that
x0 and x1 must be given (guessed) for the algorithm to start.
A program secant_method.m that solves our example problem may be written as:
function secant_method()
f = @(x) x^2 - 9;
eps = 1e-6;
x0 = 1000; x1 = x0 - 1;
[solution,no_iterations] = secant(f, x0, x1, eps);
if no_iterations > 0 % Solution found
fprintf('Number of function calls: %d\n', 2 + no_iterations);
fprintf('A solution is: %f\n', solution)
else
fprintf('Abort execution.\n')
end
end
function [solution,no_iterations] = secant(f, x0, x1, eps)
f_x0 = f(x0);
f_x1 = f(x1);
iteration_counter = 0;
while abs(f_x1) > eps && iteration_counter < 100
try
denominator = (f_x1 - f_x0)/(x1 - x0);
x = x1 - (f_x1)/denominator;
catch
fprintf('Error! - denominator zero for x = \n', x1)
break
end
x0 = x1;
x1 = x;
f_x0 = f_x1;
f_x1 = f(x1);
iteration_counter = iteration_counter + 1;
end
% Here, either a solution is found, or too many iterations
if abs(f_x1) > eps
iteration_counter = -1;
end
solution = x1;
no_iterations = iteration_counter;
end
The number of function calls is now related to no_iterations,
i.e., the number of iterations, as 2 + no_iterations, since we need
two function calls before entering the while loop, and then one
function call per loop iteration. Note that, even though we need two
points on the graph to compute each updated estimate, only a single
function call (f(x1)) is required in each iteration since
f(x0) becomes the "old" f(x1) and may simply be copied as
f_x0 = f_x1 (the exception is the very first iteration where two function
evaluations are needed).
Running secant_method.m, gives the following printout on the screen:
Number of function calls: 19
A solution is: 3.000000
As with the function Newton, we place secant in
a separate file secant.m for easy use later.