Figure 7: The integral of \( v(t) \) interpreted as the area under the graph of \( v \).
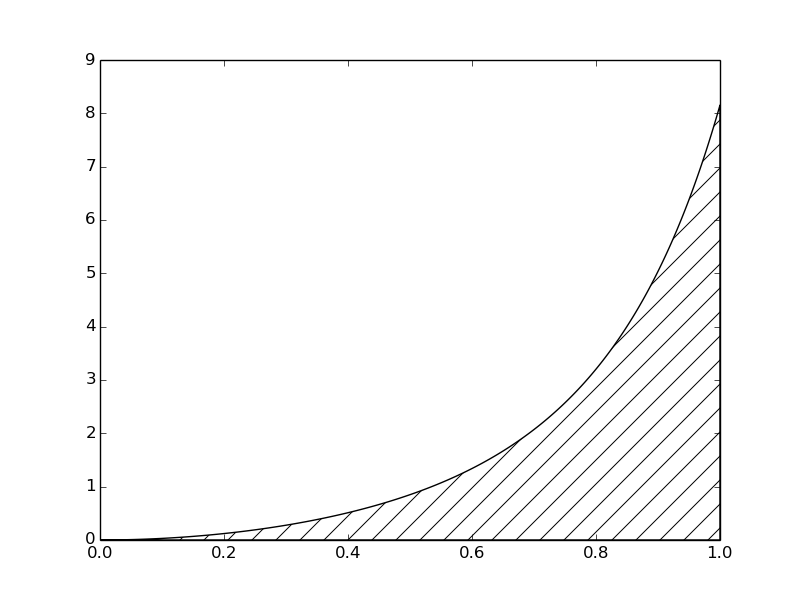
The integral \( \int_a^b f(x)dx \) may be interpreted as the area between the \( x \) axis and the graph \( y=f(x) \) of the integrand. Figure 7 illustrates this area for the choice (8). Computing the integral \( \int_0^1f(t)dt \) amounts to computing the area of the hatched region.
Figure 7: The integral of \( v(t) \) interpreted as the area under the graph of \( v \).

If we replace the true graph in Figure 7 by a set of straight line segments, we may view the area rather as composed of trapezoids, the areas of which are easy to compute. This is illustrated in Figure 8, where 4 straight line segments give rise to 4 trapezoids, covering the time intervals \( [0,0.2) \), \( [0.2,0.6) \), \( [0.6,0.8) \) and \( [0.8,1.0] \). Note that we have taken the opportunity here to demonstrate the computations with time intervals that differ in size.
Figure 8: Computing approximately the integral of a function as the sum of the areas of the trapezoids.
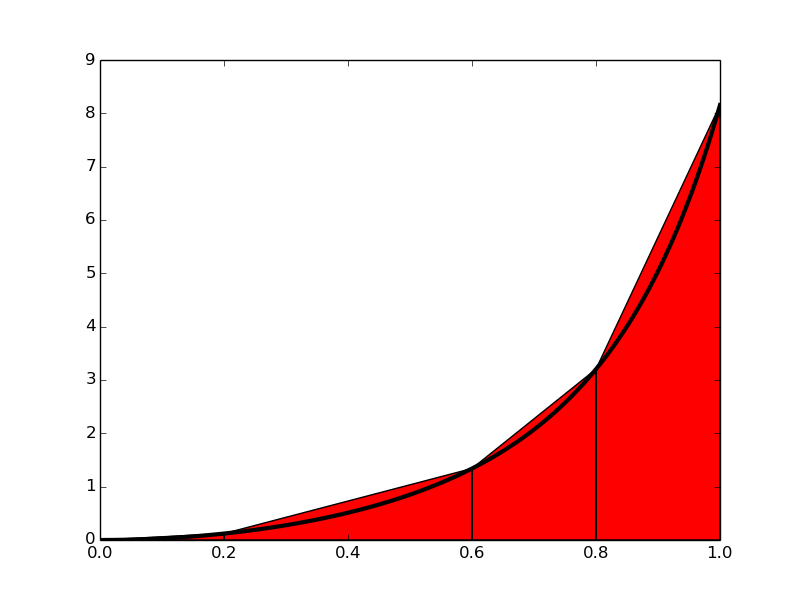
The areas of the 4 trapezoids shown in Figure 8 now constitute our approximation to the integral (8): $$ \begin{align} \int_0^1 v(t)dt &\approx h_1 (\frac{v(0)+v(0.2)}{2}) + h_2 (\frac{v(0.2)+v(0.6)}{2}) \nonumber \\ &+ h_3 (\frac{v(0.6)+v(0.8)}{2}) + h_4 (\frac{v(0.8)+v(1.0)}{2}), \tag{10} \end{align} $$ where $$ \begin{align} h_1 &= (0.2 - 0.0), \tag{11} \\ h_2 &= (0.6 - 0.2), \tag{12} \\ h_3 &= (0.8 - 0.6), \tag{13} \\ h_4 &= (1.0 - 0.8)\thinspace \tag{14} \end{align} $$ With \( v(t) = 3t^{2}e^{t^3} \), each term in (10) is readily computed and our approximate computation gives $$ \begin{equation} \int_0^1 v(t)dt \approx 1.895\thinspace . \tag{15} \end{equation} $$ Compared to the true answer of \( 1.718 \), this is off by about 10%. However, note that we used just 4 trapezoids to approximate the area. With more trapezoids, the approximation would have become better, since the straight line segments in the upper trapezoid side then would follow the graph more closely. Doing another hand calculation with more trapezoids is not too tempting for a lazy human, though, but it is a perfect job for a computer! Let us therefore derive the expressions for approximating the integral by an arbitrary number of trapezoids.
For a given function \( f(x) \), we want to approximate the integral \( \int_a^bf(x)dx \) by \( n \) trapezoids (of equal width). We start out with (6) and approximate each integral on the right hand side with a single trapezoid. In detail, $$ \begin{align} \int_a^b f(x)\,dx &= \int_{x_0}^{x_1} f(x) dx + \int_{x_1}^{x_2} f(x) dx + \ldots + \int_{x_{n-1}}^{x_n} f(x) dx, \nonumber \\ &\approx h \frac{f(x_0) + f(x_1)}{2} + h \frac{f(x_1) + f(x_2)}{2} + \ldots + \nonumber \\ &\quad h \frac{f(x_{n-1}) + f(x_n)}{2} \tag{16} \end{align} $$ By simplifying the right hand side of (16) we get $$ \begin{equation} \int_a^b f(x)\,dx \approx \\ \frac{h}{2}\left[f(x_0) + 2 f(x_1) + 2 f(x_2) + \ldots + 2 f(x_{n-1}) + f(x_n)\right] \tag{17} \end{equation} $$ which is more compactly written as $$ \begin{equation} \int_a^b f(x)\,dx \approx h \left[\frac{1}{2}f(x_0) + \sum_{i=1}^{n-1}f(x_i) + \frac{1}{2}f(x_n) \right] \thinspace . \tag{18} \end{equation} $$
The word composite is often used when a numerical integration method is applied with more than one sub-interval. Strictly speaking then, writing, e.g., "the trapezoidal method", should imply the use of only a single trapezoid, while "the composite trapezoidal method" is the most correct name when several trapezoids are used. However, this naming convention is not always followed, so saying just "the trapezoidal method" may point to a single trapezoid as well as the composite rule with many trapezoids.
Suppose our primary goal was to compute the specific integral \( \int_0^1 v(t)dt \) with \( v(t)=3t^2e^{t^3} \). First we played around with a simple hand calculation to see what the method was about, before we (as one often does in mathematics) developed a general formula (18) for the general or "abstract" integral \( \int_a^bf(x)dx \). To solve our specific problem \( \int_0^1 v(t)dt \) we must then apply the general formula (18) to the given data (function and integral limits) in our problem. Although simple in principle, the practical steps are confusing for many because the notation in the abstract problem in (18) differs from the notation in our special problem. Clearly, the \( f \), \( x \), and \( h \) in (18) correspond to \( v \), \( t \), and perhaps \( \Delta t \) for the trapezoid width in our special problem.
trapezoid(f, a, b, n) and solve the specific
problem at hand by a specialized call to this function?The first alternative in the box above sounds less abstract and therefore more attractive to many. Nevertheless, as we hope will be evident from the examples, the second alternative is actually the simplest and most reliable from both a mathematical and programming point of view. These authors will claim that the second alternative is the essence of the power of mathematics, while the first alternative is the source of much confusion about mathematics!
For the integral \( \int_a^bf(x)dx \) computed by the formula
(18) we want the corresponding Matlab function trapezoid
to take any \( f \), \( a \), \( b \), and \( n \) as input and return the
approximation to the integral.
We write a Matlab function trapezoidal
in a file trapezoidal.m
as close as possible
to the formula (18), making sure variable names correspond
to the mathematical notation:
function integral = trapezoidal(f, a, b, n)
h = (b-a)/n;
result = 0.5*f(a) + 0.5*f(b);
for i = 1:(n-1)
result = result + f(a + i*h);
end
integral = h*result;
end
trapezoidal.m to be
reused in other programs and in interactive sessions.
An interactive session can make use of the trapezoidal function
in trapezoidal.m to solve our particular problem \( \int_0^1v(t)dt \):
octave:1> v = @(t) 3*(t^2)*exp(t^3);
octave:2> n = 4;
octave:4> numerical = trapezoidal(v, 0, 1, n);
octave:5> numerical
numerical = 1.9227
octave:6> V = @(t) exp(t^3);
octave:7> exact = V(1) - V(0);
octave:8> error = exact - numerical
ans = -0.20443
octave:9> numerical = trapezoidal(v, 0, 1, 400);
octave:10> exact - numerical
ans = -2.1236e-05
Instead of computing our special problem in an interactive session, we can do it in a program. As always, a chunk of code doing a particular thing is best isolated as a function even if we do not see any future reason to call the function several times and even if we have no need for arguments to parameterize what goes on inside the function. In the present case, we just put the statements we otherwise would have put in a main program, inside a function:
function application()
v = @(t) 3*(t^2)*exp(t^3);
n = input('n: ')
numerical = trapezoidal(v, 0, 1, n);
% Compare with exact result
V = @(t) exp(t^3);
exact = V(1) - V(0);
error = exact - numerical;
fprintf("n=%d: %.16f, error: %g", n, numerical, error)
end
application() as
the only statement in the main program.
The application function and its call is in the file
trapezoidal_app.m, which can be run as
Terminal> octave trapezoidal_app.m
...
n: 4
n = 4
n=4: 1.9227167504675762, error: -0.204435
Let us illustrate the implementation implied by alternative 1 in the Programmer's dilemma box in the section Implementation. That is, we make a special-purpose code where we adapt the general formula (18) to the specific problem \( \int_0^1 3t^2e^{t^3}dt \).
Basically, we use a for loop to compute the sum. Each term with \( f(x) \) in
the formula (18) is replaced by \( 3t^2e^{t^3} \), \( x \) by \( t \),
and \( h \) by \( \Delta t \) [1]. A first try at writing a plain,
flat program doing the special calculation is
a = 0.0; b = 1.0;
n = input('n: ')
dt = (b-a)/n;
% Integral by the trapezoidal method
numerical = 0.5*3*(a^2)*exp(a^3) + 0.5*3*(b^2)*exp(b^3);
for i = 1:(n-1)
numerical = numerical + 3*((a + i*dt)^2)*exp((a + i*dt)^3);
end
numerical = numerical*dt;
exact_value = exp(1^3) - exp(0^3);
error = exact_value - numerical;
fprintf('n=%d: %.16f, error: %g', n, numerical, error);
1: Replacing \( h \) by \( \Delta t \) is not strictly required as many use \( h \) as interval also along the time axis. Nevertheless, \( \Delta t \) is an even more popular notation for a small time interval, so we adopt that common notation.
The problem with the above code is at least three-fold:
v:
v = @(t) 3*(t^2)*exp(t^3);
a = 0.0; b = 1.0;
n = input('n: ')
dt = (b-a)/n;
% Integral by the trapezoidal method
numerical = 0.5*v(a) + 0.5*v(b);
for i = 1:(n-1)
numerical = numerical + v(a + i*dt);
end
numerical = numerical*dt;
F = @(t) exp(t^3);
exact_value = F(b) - F(a);
error = exact_value - numerical;
fprintf('n=%d: %.16f, error: %g', n, numerical, error);
Unfortunately, the two other problems remain and they are fundamental.
Suppose you want to compute another integral, say \( \int_{-1}^{1.1}e^{-x^2}dx \). How much do we need to change in the previous code to compute the new integral? Not so much:
v must be replaced by a new formulaa and bt and dt changed to x and h2: You cannot integrate \( e^{-x^2} \) by hand, but this particular
integral is appearing so often in so many contexts that the integral
is a special function, called the Error function and written \( \mbox{erf}(x) \). In a code, you can
call erf(x).
These changes are straightforward to implement, but they are scattered around in the program, a fact that requires us to be very careful so we do not introduce new programming errors while we modify the code. It is also very easy to forget to make a required change.
With the previous code in trapezoidal.m, we can compute
the new integral \( \int_{-1}^{1.1}e^{-x^2}dx \) without touching
the mathematical algorithm. In an interactive session (or
in a program) we can just do
octave:1> trapezoidal(@(x) exp(-x^2), -1, 1.1, 400)
ans = 1.5269
When you now look back at the two solutions, the flat special-purpose
program and the function-based program with the general-purpose
function trapezoidal, you hopefully realize that implementing
a general mathematical algorithm in a general function requires
somewhat more abstract thinking, but the resulting code can be
used over and over again. Essentially, if you apply the flat
special-purpose style, you have to retest the implementation of
the algorithm after every change of the program.
The present integral problems result in short code. In more challenging engineering problems the code quickly grows to hundreds and thousands of line. Without abstractions in terms of general algorithms in general reusable functions, the complexity of the program grows so fast that it will be extremely difficult to make sure that the program works properly.
Another advantage of packaging mathematical algorithms in functions is that a function can be reused by anyone to solve a problem by just calling the function with a proper set of arguments. Understanding the function's inner details is not necessary to compute a new integral. Similarly, you can find libraries of functions on the Internet and use these functions to solve your problems without specific knowledge of every mathematical detail in the functions.
This desirable feature has its downside, of course: the user of a function may misuse it, and the function may contain programming errors and lead to wrong answers. Testing the output of downloaded functions is therefore extremely important before relying on the results.