This chapter is taken from the book A Primer on Scientific Programming with Python by H. P. Langtangen, 5th edition, Springer, 2016.
More on numerical Python arrays
This section lists some more advanced but useful operations with Numerical Python arrays.
Copying arrays
Let x be an array. The statement a = x makes a refer to the same
array as x. Changing a will then also affect x:
>>> import numpy as np
>>> x = np.array([1, 2, 3.5])
>>> a = x
>>> a[-1] = 3 # this changes x[-1] too!
>>> x
array([ 1., 2., 3.])
Changing a without changing x requires a to be a copy of x:
>>> a = x.copy()
>>> a[-1] = 9
>>> a
array([ 1., 2., 9.])
>>> x
array([ 1., 2., 3.])
In-place arithmetics
Let a and b be two arrays of the same shape. The expression a +=
b means a = a + b, but this is not the complete story. In the
statement a = a + b, the sum a + b is first computed, yielding a
new array, and then the name a is bound to this new array. The old
array a is lost unless there are other names assigned to this array.
In the statement a += b, elements of b are added directly into the
elements of a (in memory). There is no hidden intermediate array as
in a = a + b. This implies that a += b is more efficient than a
= a + b since Python avoids making an extra array. We say that the
operators +=, *=, and so on, perform in-place arithmetics in
arrays.
Consider the compound array expression
a = (3*x**4 + 2*x + 4)/(x + 1)
The computation actually goes as follows with seven hidden arrays for storing intermediate results:
-
r1 = x**4 -
r2 = 3*r1 -
r3 = 2*x -
r4 = r2 + r3 -
r5 = r4 + 4 -
r6 = x + 1 -
r7 = r5/r6 -
a = r7
a = x.copy()
a **= 4
a *= 3
a += 2*x
a += 4
a /= x + 1
The three extra arrays in this series of statement arise from copying
x, and computing the right-hand sides 2*x and x+1.
Quite often in computational science and engineering, a huge number of arithmetics is performed on very large arrays, and then saving memory and array allocation time by doing in-place arithmetics is important.
The mix of assignment and in-place arithmetics makes it easy to make
unintended changes of more than one array. For example, this code
changes x:
a = x
a += y
since a refers to the same array as x and the change of
a is done in-place.
Allocating arrays
We have already seen that the np.zeros function is handy for making
a new array a of a given size. Very often the size and the type of
array elements have to match another existing array x. We can then
either copy the original array, e.g.,
a = x.copy()
and fill elements in a with the right new values, or we can
say
a = np.zeros(x.shape, x.dtype)
The attribute x.dtype holds the array element type (dtype for
data type), and x.shape is a tuple with
the array dimensions. The variable a.ndim holds the number of
dimensions.
Sometimes we may want to ensure that an object is an array, and if
not, turn it into an array. The np.asarray function is useful in
such cases:
a = np.asarray(a)
Nothing is copied if a already is an array, but if a is a list
or tuple, a new array with a copy of the data is created.
Generalized indexing
The section Basics of numerical Python arrays shows how slices can be used to
extract and manipulate subarrays. The slice f:t:i corresponds to
the index set f, f+i, f+2*i, ... up to, but not including, t.
Such an index set can be given explicitly too: a[range(f,t,i)].
That is, the integer list from range can be used as a set of
indices. In fact, any integer list or integer array can be used as
index:
>>> a = np.linspace(1, 8, 8)
>>> a
array([ 1., 2., 3., 4., 5., 6., 7., 8.])
>>> a[[1,6,7]] = 10
>>> a
array([ 1., 10., 3., 4., 5., 6., 10., 10.])
>>> a[range(2,8,3)] = -2 # same as a[2:8:3] = -2
>>> a
array([ 1., 10., -2., 4., 5., -2., 10., 10.])
We can also use boolean arrays to generate an index set. The indices
in the set will correspond to the indices for which the boolean array
has True values. This functionality allows expressions like
a[x<m]. Here are two examples, continuing the previous interactive
session:
>>> a[a < 0] # pick out the negative elements of a
array([-2., -2.])
>>> a[a < 0] = a.max()
>>> a
array([ 1., 10., 10., 4., 5., 10., 10., 10.])
>>> # Replace elements where a is 10 by the first
>>> # elements from another array/list:
>>> a[a == 10] = [10, 20, 30, 40, 50, 60, 70]
>>> a
array([ 1., 10., 20., 4., 5., 30., 40., 50.])
Generalized indexing using integer arrays or lists is important for vectorized initialization of array elements. The syntax for generalized indexing of higher-dimensional arrays is slightly different, see the section Two-dimensional numerical Python arrays.
Testing for the array type
Inside an interactive Python shell you can easily check an object's type
using the type
In case of a Numerical Python array, the type name is ndarray:
>>> a = np.linspace(-1, 1, 3)
>>> a
array([-1., 0., 1.])
>>> type(a)
<type 'numpy.ndarray'>
Sometimes you need to test if a variable is an ndarray or a float
or int. The isinstance function can be used this purpose:
>>> isinstance(a, np.ndarray)
True
>>> isinstance(a, (float,int)) # float or int?
False
A typical use of isinstance and type to check on object's type is
shown next.
Example: Vectorizing a constant function
Suppose we have a constant function,
def f(x):
return 2
This function accepts an array argument x, but will return a float
while a vectorized version of the function should return an array of
the same shape as x where each element has the value 2. The
vectorized version can be realized as
def fv(x):
return np.zeros(x.shape, x.dtype) + 2
The optimal vectorized function would be one that works for both a scalar and an array argument. We must then test on the argument type:
def f(x):
if isinstance(x, (float, int)):
return 2
elif isinstance(x, np.ndarray):
return np.zeros(x.shape, x.dtype) + 2
else:
raise TypeError\
('x must be int, float or ndarray, not %s' % type(x))
Compact syntax for array generation
There is a special compact syntax r_[f:t:s] for the linspace
function:
>>> a = r_[-5:5:11j] # same as linspace(-5, 5, 11)
>>> print a
[-5. -4. -3. -2. -1. 0. 1. 2. 3. 4. 5.]
Here, 11j means 11 coordinates (between -5 and 5, including the
upper limit 5). That is, the number of elements in the array is given
with the imaginary number syntax.
Shape manipulation
The shape attribute in array objects holds the shape, i.e., the size
of each dimension. A function size returns the total number of
elements in an array. Here are a few equivalent ways of changing the
shape of an array:
>>> a = np.linspace(-1, 1, 6)
>>> print a
[-1. -0.6 -0.2 0.2 0.6 1. ]
>>> a.shape
(6,)
>>> a.size
6
>>> a.shape = (2, 3)
>>> a = a.reshape(2, 3) # alternative
>>> a.shape
(2, 3)
>>> print a
[[-1. -0.6 -0.2]
[ 0.2 0.6 1. ]]
>>> a.size # total no of elements
6
>>> len(a) # no of rows
2
>>> a.shape = (a.size,) # reset shape
Note that len(a) always returns the length of the first
dimension of an array.
High-performance computing with arrays
Programs with lots of array calculations may soon consume much time and memory, so it may quickly become crucial to speed up calculations and use as little memory as possible. The main technique for speeding up array calculations is vectorization, i.e., avoiding explicit loops in Python over array elements. To save memory usage, one needs to understand when arrays get allocated and avoid this by in-place array arithmetics.
Example: axpy
Our computational case study concerns the famous "axpy" operation: \( r = ax + y \), where \( a \) is a number and \( x \) and \( y \) are arrays. All implementations and the associated experimentation are found in the file hpc_axpy.py.
Scalar implementation
A naive loop implementation of the "axpy" operation \( ax+y \) reads
def axpy_loop_newr(a, x, y):
r = np.zeros_like(x)
for i in range(r.size):
r[i] = a*x[i] + y[i]
return r
Classical implementations overwrite \( y \) by \( ax + y \): \( y \leftarrow ax+y \), but we shall make implementations where we either can overwrite \( y \) or place \( ax+y \) in another array. The function above creates a new array for the result.
Rather than allocating the array inside the function, we can put that
burden on the user and provide a result array r as input:
def axpy_loop(a, x, y, r):
for i in range(r.size):
r[i] = a*x[i] + y[i]
return r
The advantage of this version is that we can either overwrite \( y \) by \( ax+y \) or store \( ax+y \) in a separate array:
# Classical axpy
y = axpy_loop(a, x, y, y)
# Store axpy result in separate array
r = np.zeros_like(x)
r = axpy_loop(a, x, y, r)
r = axpy_loop(a, x, y, r)
can equally well be written
axpy_loop(a, x, y, r)
This is the typical coding style in Fortran, C, or C++ (where r is then
transferred as a reference or pointer to the array data).
In Python, there is no need for the function axpy_loop to return r, because
the assignment to r[i] inside the loop changes all elements of the
r. The array r will therefore be modified after calling
axpy_loop(a, x, y, r) anyway. However, it is a good convention in Python
that all input data to a function are arguments and all output data
are returned. With
r = axpy_loop(a, x, y, r)
we clearly see that r is both input and output.
Vectorized implementation
The vectorized implementation of the "axpy" operation reads
def axpy1(a, x, y):
r = a*x + y
return r
Note that the result is placed in a new array r arising from the
operation a*x+y.
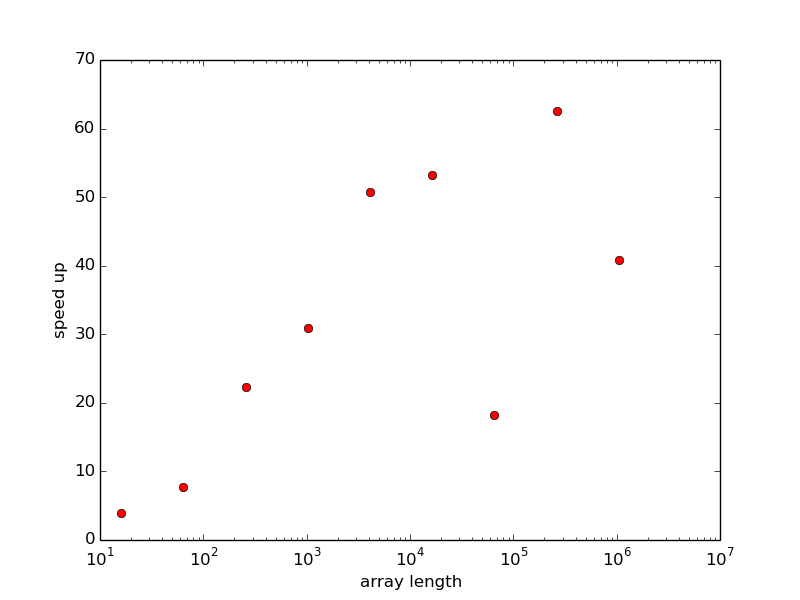
The speed up of vectorization is significant, see
Figure 11 (made by the function effect_of_vec
in the file hpc_axpy.py).
Figure 11: Improved efficiency of vectorizing the "axpy" operation as function of array length.
Temporary arrays are needed in the vectorized implementation.
One would expect that a*x must be calculated and stored in
a temporary array, call it r1, and then r1 + y must be
evaluated and stored in another allocated array r, which is returned.
It appears that a*x + y only needs the allocation of one array,
the one to be returned (we have investigated the memory consumption
in detail using the memory_profiler module). Anyway, repeated
calls to axpy1 with large arrays lead to an allocation of a new
large array in each call.
Memory-saving implementation
Applications with large arrays should avoid unnecessary allocation
of temporary arrays and instead reuse pre-allocated arrays.
Suppose we have allocated an array for the result r = ax + y once
and for all. We can pass the r array to the computing function
as in the axpy_loop function above and use the memory in r
for intermediate calculation. In vectorized code, this requires
use of in-place array
arithmetics. For example, u += v adds each element in v into
u. The mathematically equivalent construction u = u + v would
first create an object from u + v and then assign the name u
to this object. Similarly, u *= a multiplies all elements in u
by the number a. Other in-place operators are -= for
elementwise subtraction,
/= for elementwise division, and **= for elementwise exponentiation.
In-place arithmetics for doing r = a*x + y in a pre-allocated
array r will first copy all elements of x into r, then
perform elementwise multiplication by a, and finally elementwise
addition of y:
def axpy2(a, x, y, r):
r[:] = x
r *= a
r += y
return r
Note that r[:] = x inserts the elements of x into r.
A mathematically equivalent construction, r = x.copy(), allocates
a new object and fills it with the values of x before the name
r refers to this object. The array r supplied as argument to the
function is then lost, and the returned array is another object.
We can perform repeated calls to the axpy2 function without any
extra memory allocation. This can be proved by a small code snippet
where we use id(r) to see the unique identity of the r array.
If this identity remains constant through calls, we always reuse
the pre-allocated r array:
r = np.zeros_like(x)
print id(r)
for i in range(10):
r = axpy2(a, x, y, r)
print id(r)
The output prints the same number, proving that it is physically the
same object we feed as r to axpy2 that is also returned.
We can equally well drop returning r and utilize that the changes
made by in-place arithmetics is always reflected in the r array
we allocate outside the function:
def axpy3(a, x, y, r):
r[:] = x
r *= a
r += y
The call can now just be
axpy3(a, x, y, r)
However, as emphasized in the section Scalar implementation, in Python we usually return the output data (because this is no extra cost, only references to objects are physically transferred back to the calling code).
Analysis of memory usage
The module memory_profiler is very useful for analyzing the memory
usage of every statement in a program. The module is installed
by
Terminal> sudo pip install memory_profiler
Each function we want to
analyze must have (the decorator) @profile at the line above, e.g.,
@profile
def axpy1(a, x, y:
r = a*x + y
return r
We can then run a program with name axpy.py by
Terminal> python -m memory_profiler axpy.py
The arrays must be quite large to see a significant increase in memory usage. With 10,000,000 elements in each array we get output like
Line # Mem usage Increment Line Contents
================================================
1 251.977 MiB 0.000 MiB @profile
2 def axpy1(a, x, y:
3 328.273 MiB 76.297 MiB r = a*x + y
4 328.273 MiB 0.000 MiB return r
Line # Mem usage Increment Line Contents
================================================
6 251.977 MiB 0.000 MiB @profile
7 def axpy2(a, x, y, r):
8 251.977 MiB 0.000 MiB r[:] = x
9 251.977 MiB 0.000 MiB r *= a
10 251.977 MiB 0.000 MiB r += y
11 251.977 MiB 0.000 MiB return r
This demonstrates the larger memory consumption of axpy1 compared
with axpy2.
Analysis of the CPU time
The module line_profiler can time each line of a program.
Installation is easily done by sudo pip install line_profiler.
As for module_profiler described in the previous section,
also line_profiler requires each function to be analyzed to
have (the decorator) @profile at the line above the function.
The module is installed together with an analysis script
kernprof that we use to run the program:
Terminal> kernprof -l -v axpy.py
With an array length of 500,000 we get output like
Total time: 0.014291 s
Function: axpy1 at line 1
Line # Hits Time Per Hit % Time Line Contents
==============================================================
1 @profile
2 def axpy1(a, x, y):
3 3 14283 4761.0 99.9 r = a*x + y
4 3 8 2.7 0.1 return r
Total time: 0.004382 s
Function: axpy2 at line 6
Line # Hits Time Per Hit % Time Line Contents
==============================================================
6 @profile
7 def axpy2(a, x, y, r):
8 3 1981 660.3 45.2 r[:] = x
9 3 1258 419.3 28.7 r *= a
10 3 1138 379.3 26.0 r += y
11 3 5 1.7 0.1 return r
Total time: 1.38674 s
Function: axpy_loop at line 26
Line # Hits Time Per Hit % Time Line Contents
==============================================================
26 @profile
27 def axpy_loop(a, x, y, r):
28 1500006 449747 0.3 32.4 for i in range(r.size):
29 1500003 936985 0.6 67.6 r[i] = a*x[i] + y[i]
30 3 10 3.3 0.0 return r
We see that the administration of the for loop takes 1/3 of the total cost of the loop.
Both line_profiler and memory_profiler are very useful tools
for spotting inefficient constructions in a code.