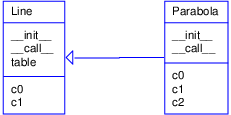
Figure 1: UML diagram for the class hierarchy with superclass Line and subclass Parabola.
This chapter is taken from the book A Primer on Scientific Programming with Python by H. P. Langtangen, 5th edition, Springer, 2016.
Most of this document tells you how to put related classes together in families such that the family can be viewed as one unit. This idea helps to hide details in a program, and makes it easier to modify or extend the program.
A family of classes is known as a class hierarchy. As in a biological family, there are parent classes and child classes. Child classes can inherit data and methods from parent classes, they can modify these data and methods, and they can add their own data and methods. This means that if we have a class with some functionality, we can extend this class by creating a child class and simply add the functionality we need. The original class is still available and the separate child class is small, since it does not need to repeat the code in the parent class.
The magic of object-oriented programming is that other parts of the
code do not need to distinguish whether an object is the parent or the
child - all generations in a family tree can be treated as a unified
object. In other words, one piece of code can work with all members in
a class family or hierarchy. This principle has revolutionized the
development of large computer systems. As an illustration, two of the
most widely used computer languages today are Java and C#, and both
of them force programs to be written in an object-oriented style.
The concepts of classes and object-oriented programming first appeared in the Simula programming language in the 1960s. Simula was invented by the Norwegian computer scientists Ole-Johan Dahl and Kristen Nygaard, and the impact of the language is particularly evident in C++, Java, and C#, three of the most dominating programming languages in the world today. The invention of object-oriented programming was a remarkable achievement, and the professors Dahl and Nygaard received two very prestigious prizes: the von Neumann medal and the Turing prize (popularly known as the Nobel prize of computer science).
A parent class is usually called base class or superclass, while the child class is known as a subclass or derived class. We shall use the terms superclass and subclass from now on.
Assume that we have written a class for straight lines, \( y=c_0 + c_1x \):
class Line(object):
def __init__(self, c0, c1):
self.c0 = c0
self.c1 = c1
def __call__(self, x):
return self.c0 + self.c1*x
def table(self, L, R, n):
"""Return a table with n points for L <= x <= R."""
s = ''
import numpy as np
for x in np.linspace(L, R, n):
y = self(x)
s += '%12g %12g\n' % (x, y)
return s
__init__ initializes the coefficients \( c_0 \) and
\( c_1 \) in the expression for the straight line: \( y=c_0 + c_1x \). The
call operator __call__ evaluates the function \( c_1x+c_0 \), while the
table method samples the function at n points and creates a table
of \( x \) and \( y \) values.
A parabola \( y=c_0 + c_1x + c_2x^2 \) contains a straight line as a special case (\( c_2=0 \)). A class for parabolas will therefore be similar to a class for straight lines. All we have do to is to add the new term \( c_2x^2 \) in the function evaluation and store \( c_2 \) in the constructor:
class Parabola(object):
def __init__(self, c0, c1, c2):
self.c0 = c0
self.c1 = c1
self.c2 = c2
def __call__(self, x):
return self.c2*x**2 + self.c1*x + self.c0
def table(self, L, R, n):
"""Return a table with n points for L <= x <= R."""
s = ''
import numpy as np
for x in np.linspace(L, R, n):
y = self(x)
s += '%12g %12g\n' % (x, y)
return s
table method from class Line
without any modifications.
Python and other languages that support object-oriented programming
have a special construct, so that class Parabola does not need
to repeat the code that we have already written in class Line.
We can specify that class Parabola inherits all code from class
Line by adding (Line) in the class headline:
class Parabola(Line):
Parabola now automatically gets all the code from class
Line. Exercise 1: Demonstrate the magic of inheritance asks you to explicitly demonstrate
the validity of this assertion. We say that class Parabola is
derived from class Line, or equivalently, that class Parabola is
a subclass of its superclass Line.
Now, class Parabola should not be identical to class Line: it
needs to add data in the constructor (for the new term) and to modify
the call operator (because of the new term), but the table method
can be inherited as it is. If we implement the constructor and the
call operator in class Parabola, these will override the inherited
versions from class Line. If we do not implement a table method,
the one inherited from class Line is available as if it were coded
visibly in class Parabola.
Class Parabola must first have the statements from the class Line
methods __call__ and __init__, and then add extra code in these
methods. An important principle in computer programming is to avoid
repeating code. We should therefore call up functionality in class
Line instead of copying statements from class Line methods to
Parabola methods. Any method in the superclass Line can be called
using the syntax
Line.methodname(self, arg1, arg2, ...)
# or
super(Parabola, self).methodname(arg1, arg2, ...)
object (i.e., class Line must be a
new-style class).
Let us now show how to write class Parabola as a subclass of class
Line, and implement just the new additional code that we need and
that is not already written in the superclass:
class Parabola(Line):
def __init__(self, c0, c1, c2):
Line.__init__(self, c0, c1) # let Line store c0 and c1
self.c2 = c2
def __call__(self, x):
return Line.__call__(self, x) + self.c2*x**2
Parabola provides exactly the
same functionality as the first version of class Parabola that
we showed in the section A first try on a class for parabolas and that did not inherit
from class Line. Figure 1 shows the
class hierarchy in UML fashion. The arrow from one class to another
indicates inheritance.
Figure 1: UML diagram for the class hierarchy with superclass Line and subclass Parabola.

A quick demo of the Parabola class in a main program,
p = Parabola(1, -2, 2)
p1 = p(x=2.5)
print p1
print p.table(0, 1, 3)
8.5
0 1
0.5 0.5
1 1
The program flow can be somewhat complicated when we work with class hierarchies. Consider the code segment
p = Parabola(1, -1, 2)
p1 = p(x=2.5)
Calling Parabola(1, -1, 2) leads to a call to the constructor method
__init__, where the arguments c0, c1, and c2 in this case are
int objects with values 1, -1, and 2. The self argument in the
constructor is the object that will be returned and referred to by the
variable p. Inside the constructor in class Parabola we call the
constructor in class Line. In this latter method, we create two
data attributes in the self object. Printing out dir(self) will
explicitly demonstrate what self contains so far in the construction
process. Back in class Parabola's constructor, we add a third
attribute c2 to the same self object. Then the self object is
invisibly returned and referred to by p.
The other statement, p1 = p(x=2.5), has a similar program
flow. First we enter the p.__call__ method with self as p and
x as a float object with value 2.5. The program flow jumps to the
__call__ method in class Line for evaluating the linear part
\( c_1x+c_0 \) of the expression for the parabola, and then the flow jumps
back to the __call__ method in class Parabola where we add the new
quadratic term.
Python has the function isinstance(i,t) for checking if an
instance i is of class type t:
>>> l = Line(-1, 1)
>>> isinstance(l, Line)
True
>>> isinstance(l, Parabola)
False
Line is not a Parabola, but is a Parabola a
Line?
>>> p = Parabola(-1, 0, 10)
>>> isinstance(p, Parabola)
True
>>> isinstance(p, Line)
True
Parabola
instance is regarded as a
Line instance too, since it contains everything that a Line
instance contains.
Every instance has an attribute __class__ that holds the
type of class:
>>> p.__class__
<class __main__.Parabola at 0xb68f108c>
>>> p.__class__ == Parabola
True
>>> p.__class__.__name__ # string version of the class name
'Parabola'
p.__class__ is a class object (or class
definition one may say), while p.__class__.__name__
is a string.
These two variables can be used as an alternative test for
the class type:
if p.__class__.__name__ == 'Parabola':
...
# or
if p.__class__ == Parabola:
...
isinstance(p, Parabola) is the recommended programming style
for checking the type of an object.
A function
issubclass(c1, c2) tests if class c1 is a subclass of class
c2, e.g.,
>>> issubclass(Parabola, Line)
True
>>> issubclass(Line, Parabola)
False
__bases__ attribute of the class object:
>>> p.__class__.__bases__
(<class __main__.Line at 0xb7c5d2fc>,)
>>> p.__class__.__bases__[0].__name__ # extract name as string
'Line'
Instead of letting class Parabola
inherit from a class Line, we may let it contain a
class Line instance as a data attribute:
class Parabola(object):
def __init__(self, c0, c1, c2):
self.line = Line(c0, c1) # let Line store c0 and c1
self.c2 = c2
def __call__(self, x):
return self.line(x) + self.c2*x**2
If it is natural to say that class Parabola is a Line object, we
say that Parabola has an is-a relationship with class
Line. Alternatively, if it is natural to think that class Parabola
has a Line object, we speak about a has-a relationship with
class Line. In the present example, we may argue that technically
the expression for the parabola is a straight line plus another term
and hence claim an is-a relationship, but we can also view a parabola
as a quantity that has a line plus an extra term, which makes the
has-a relationship relevant.
From a mathematical point of view, many will say that a parabola is
not a line, but that a line is a special case of a parabola.
Adopting this reasoning reverses the dependency of the classes: now it
is more natural to let Line is a subclass of Parabola (Line is
a Parabola). This easy, and all we have to do is
class Parabola(object):
def __init__(self, c0, c1, c2):
self.c0, self.c1, self.c2 = c0, c2, c2
def __call__(self, x):
return self.c0 + self.c1*x + self.c2*x**2
def table(self, L, R, n): # implemented as shown above
class Line(Parabola):
def __init__(self, c0, c1):
Parabola.__init__(self, c0, c1, 0)
__call__ method from class Parabola will
work since the c2 coefficient is zero.
Exercise 4: Create an alternative class hierarchy for polynomials suggests deriving Parabola from
a general class Polynomial and asks you to discuss the alternative class
designs.
In the example where Parabola as a subclass of Line, we
used inheritance to extend the functionality of the superclass.
The case where Line is a subclass of Parabola is an example on
restricting the superclass functionality in a subclass.
How classes depend on each other is influenced by two factors: sharing
of code and logical relations. From a sharing of code perspective,
many will say that class Parabola is naturally a subclass of Line,
the former adds code to the latter. On the other hand, Line is
naturally a subclass of Parabola from the logical relations in
mathematics. Computational efficiency is a third perspective when we
implement mathematics. When Line is a subclass of Parabola we
always evaluate the \( c_2x^2 \) term in the parabola although this term
is zero. Nevertheless, when Parabola is a subclass of Line, we
call Line.__call__ to evaluate the linear part of the second-degree
polynomial, and this call is costly in Python. From a pure efficiency
point of view, we would reprogram the linear part in
Parabola.__call__ (which is against the programming habit we have
been arguing for!). This little discussion here highlights the many
different considerations that come into play when establishing class
relations.
As another example of class hierarchies, we now want to represent
functions by classes, as described in the document
Introduction to classes in Python
[2], but in addition to the __call__
method, we also want to provide methods for the first and second
derivative. The class can be sketched as
class SomeFunc(object):
def __init__(self, parameter1, parameter2, ...)
# Store parameters
def __call__(self, x):
# Evaluate function
def df(self, x):
# Evaluate the first derivative
def ddf(self, x):
# Evaluate the second derivative
class FuncWithDerivatives(object):
def __init__(self, h=1.0E-5):
self.h = h # spacing for numerical derivatives
def __call__(self, x):
raise NotImplementedError\
('___call__ missing in class %s' % self.__class__.__name__)
def df(self, x):
"""Return the 1st derivative of self.f."""
# Compute first derivative by a finite difference
h = self.h
return (self(x+h) - self(x-h))/(2.0*h)
def ddf(self, x):
"""Return the 2nd derivative of self.f."""
# Compute second derivative by a finite difference:
h = self.h
return (self(x+h) - 2*self(x) + self(x-h))/(float(h)**2)
class MyFunc(FuncWithDerivatives):
def __init__(self, a):
self.a = a
def __call__(self, x):
return cos(self.a*x) + x**3
def df(self, x):
a = self.a
return -a*sin(a*x) + 3*x**2
def ddf(self, x):
a = self.a
return -a*a*cos(a*x) + 6*x
h is never
initialized, and there are no possibilities for using numerical
approximations via the superclass methods
df and ddf.
Instead, we override all the inherited methods and implement our own
versions.
Many think it is a good programming style to always call the superclass constructor in a subclass constructor, even in simple classes where we do not need the functionality of the superclass constructor.
For a more complicated function, e.g., \( f(x)=\ln |p\tanh(qx\cos rx)| \), we may skip the analytical derivation of the derivatives, and just code \( f(x) \) and rely on the difference approximations inherited from the superclass to compute the derivatives:
class MyComplicatedFunc(FuncWithDerivatives):
def __init__(self, p, q, r, h=1.0E-5):
FuncWithDerivatives.__init__(self, h)
self.p, self.q, self.r = p, q, r
def __call__(self, x):
return log(abs(self.p*tanh(self.q*x*cos(self.r*x))))
>>> f = MyComplicatedFunc(1, 1, 1)
>>> x = pi/2
>>> f(x)
-36.880306514638988
>>> f.df(x)
-60.593693618216086
>>> f.ddf(x)
3.3217246931444789e+19
MyComplicatedFunc inherits the df and ddf methods from the
superclass FuncWithDerivatives. These methods compute the first and
second derivatives approximately, provided that we have defined a
__call__ method. If we fail to define this method, we will inherit
__call__ from the superclass, which just raises an exception, saying
that the method is not properly implemented in class
MyComplicatedFunc.
The important message in this subsection is that we introduced a super
class to mainly define an interface, i.e., the operations (in terms
of methods) that one can do with a class in this class hierarchy. The
superclass itself is of no direct use, since it does not implement any
function evaluation in the __call__ method. However, it stores a
variable common to all subclasses (h), and it implements general
methods df and ddf that any subclass can make use of. A specific
mathematical function must be represented as a subclass, where the
programmer can decide whether analytical derivatives are to be used,
or if the more lazy approach of inheriting general functionality (df
and ddf) for computing numerical derivatives is satisfactory.
In object-oriented programming, the superclass very often defines an interface, and instances of the superclass have no applications on their own - only instances of subclasses can do anything useful.
To digest the present material on inheritance, we recommend doing Exercise 1: Demonstrate the magic of inheritance-Exercise 4: Create an alternative class hierarchy for polynomials before reading the next section.