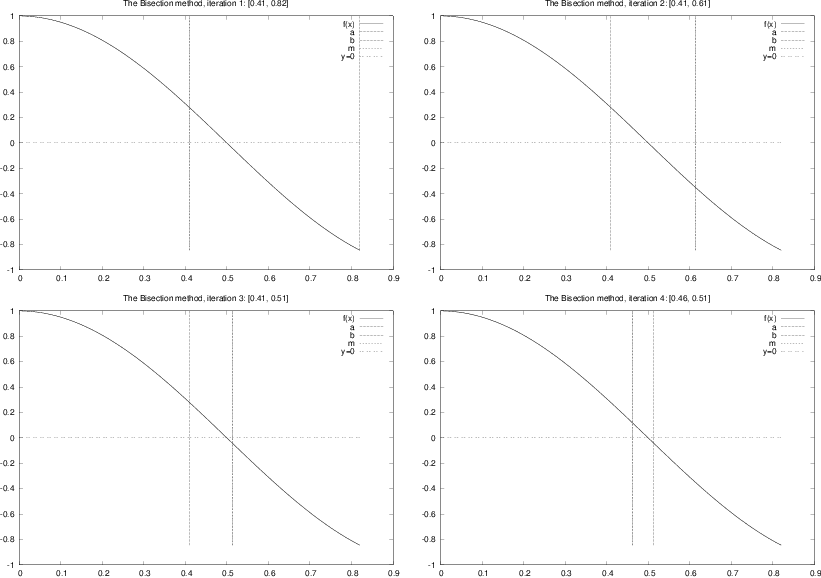
Figure 2: Illustration of the first four iterations of the Bisection algorithm for solving \( \cos (\pi x) =0 \). The vertical lines correspond to the current value of \( a \) and \( b \).
This chapter is taken from the book A Primer on Scientific Programming with Python by H. P. Langtangen, 5th edition, Springer, 2016.
Prompting the user and reading the answer back into a variable is done by
var = raw_input('Give value: ')
raw_input function returns a string containing the
characters that the user wrote on the keyboard before pressing the Return
key. It is necessary to convert var to an appropriate object
(int or float, for instance)
if we want to perform mathematical operations with var.
Sometimes
var = eval(raw_input('Give value: '))
scitools.misc.str2obj:
from scitools.misc import str2obj
var = str2obj(raw_input('Give value: '))
3 makes var refer to an int object, 3.14
results in a float object, [-1,1] results in a list, (1,3,5,7)
in a tuple, and some text in the string (str) object 'some
text' (run the program str2obj_demo.py to see this functionality
demonstrated).
The sys.argv[1:] list contains all the command-line arguments
given to a program (sys.argv[0] contains the program name).
All elements in sys.argv are strings. A typical usage is
parameter1 = float(sys.argv[1])
parameter2 = int(sys.argv[2])
parameter3 = sys.argv[3] # parameter3 can be string
The argparse module is recommended for
interpreting command-line arguments of the form --option value.
A simple recipe with argparse reads
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--p1', '--parameter_1', type=float,
default=0.0, help='1st parameter')
parser.add_argument('--p2', type=float,
default=0.0, help='2nd parameter')
args = parser.parse_args()
p1 = args.p1
p2 = args.p2
--parameter_1 --p1 --p2
argparse is very flexible can easily handle options
without values or command-line arguments without any
option specifications.
Calling eval(s) turns a string s, containing a Python
expression, into code as if the contents of the string were written
directly into the program code. The result of the following
eval call is a float object holding the number 21.1:
>>> x = 20
>>> r = eval('x + 1.1')
>>> r
21.1
>>> type(r)
<type 'float'>
exec function takes a string with arbitrary Python code
as argument and executes the code. For example, writing
exec("""
def f(x):
return %s
""" % sys.argv[1])
sys.argv[1]
into a function definition in the program.
Given a mathematical formula as a string, s, we can turn this
formula into a callable Python function f(x) by
from scitools.std import StringFunction
f = StringFunction(s)
x:
Q_formula = 'amplitude*sin(w*t-phaseshift)'
Q = StringFunction(Q_formula, independent_variable='t',
amplitude=1.5, w=pi, phaseshift=0)
values1 = [Q(i*0.1) for t in range(10)]
Q.set_parameters(phaseshift=pi/4, amplitude=1)
values2 = [Q(i*0.1) for t in range(10)]
f = StringFunction('x+y**2+A', independent_variables=('x', 'y'),
A=0.2)
x = 1; y = 0.5
print f(x, y)
Reading from or writing to a file first requires that the file is opened, either for reading, writing, or appending:
infile = open(filename, 'r') # read
outfile = open(filename, 'w') # write
outfile = open(filename, 'a') # append
with:
with open(filename, 'r') as infile: # read
with open(filename, 'w') as outfile: # write
with open(filename, 'a') as outfile: # append
line = infile.readline() # read the next line
filestr = infile.read() # read rest of file into string
lines = infile.readlines() # read rest of file into list
for line in infile: # read rest of file line by line
outfile.write(s)
s is a string. Contrary to print s,
no newline is added to s in outfile.write(s).
After reading or writing is finished, the file must be closed:
somefile.close()
with statement for
reading or writing files:
with open(filename, 'w') as outfile:
for var1, var2 in data:
outfile.write('%5.2f %g\n' % (var1, var2))
# outfile is closed
Testing for potential errors is done with try-except blocks:
try:
<statements>
except ExceptionType1:
<provide a remedy for ExceptionType1 errors>
except ExceptionType2, ExceptionType3, ExceptionType4:
<provide a remedy for three other types of errors>
except:
<provide a remedy for any other errors>
...
NameError for an undefined variable, TypeError for an
illegal value
in an operation, and IndexError for a list index out of bounds.
When some error is encountered in a program, the programmer can raise an exception:
if z < 0:
raise ValueError('z=%s is negative - cannot do log(z)' % z)
r = log(z)
A module is created by putting a set of functions
in a file. The filename (minus the required extension .py)
is the name of the module.
Other programs can import the module only if it resides in the
same folder or in a folder contained in the sys.path
list (see the section Using modules for how to
deal with this potential problem).
Optionally, the module file can have a special if construct
at the end, called test block, which tests the module or demonstrates
its usage. The test block does not get executed when the module is
imported in another program, only when the module file is run as
a program.
The important computer science topics and Python tools in this document are
sys.argvraw_inputeval and execThe summarizing example of this document concerns the implementation of the Bisection method for solving nonlinear equations of the form \( f(x)=0 \) with respect to \( x \). For example, the equation $$ \begin{equation*} x = 1 + \sin x\end{equation*} $$ can be cast in the form \( f(x)=0 \) if we move all terms to the left-hand side and define \( f(x)=x-1-\sin x \). We say that \( x \) is a root of the equation \( f(x)=0 \) if \( x \) is a solution of this equation. Nonlinear equations \( f(x)=0 \) can have zero, one, several, or infinitely many roots.
Numerical methods for computing roots normally lead to approximate results only, i.e., \( f(x) \) is not made exactly zero, but very close to zero. More precisely, an approximate root \( x \) fulfills \( |f(x)|\leq\epsilon \), where \( \epsilon \) is a small number. Methods for finding roots are of an iterative nature: we start with a rough approximation to a root and perform a repetitive set of steps that aim to improve the approximation. Our particular method for computing roots, the Bisection method, guarantees to find an approximate root, while other methods, such as the widely used Newton's method, can fail to find roots.
The idea of the Bisection method is to start with an interval \( [a,b] \) that contains a root of \( f(x) \). The interval is halved at \( m=(a+b)/2 \), and if \( f(x) \) changes sign in the left half interval \( [a,m] \), one continues with that interval, otherwise one continues with the right half interval \( [m,b] \). This procedure is repeated, say \( n \) times, and the root is then guaranteed to be inside an interval of length \( 2^{-n}(b-a) \). The task is to write a program that implements the Bisection method and verify the implementation.
To implement the Bisection method, we need to translate the description in the previous paragraph to a precise algorithm that can be almost directly translated to computer code. Since the halving of the interval is repeated many times, it is natural to do this inside a loop. We start with the interval \( [a,b] \), and adjust \( a \) to \( m \) if the root must be in the right half of the interval, or we adjust \( b \) to \( m \) if the root must be in the left half. In a language close to computer code we can express the algorithm precisely as follows:
for i in range(0, n+1):
m = (a + b)/2
if f(a)*f(m) <= 0:
b = m # root is in left half
else:
a = m # root is in right half
# f(x) has a root in [a,b]
Figure 2 displays graphically
the first four steps of
this algorithm for solving the equation \( \cos (\pi x)=0 \), starting
with the interval \( [0, 0.82] \). The graphs are automatically produced
by the program bisection_movie.py, which was run as follows
for this particular example:
bisection_movie.py 'cos(pi*x)' 0 0.82
Figure 2: Illustration of the first four iterations of the Bisection algorithm for solving \( \cos (\pi x) =0 \). The vertical lines correspond to the current value of \( a \) and \( b \).

In the algorithm listed above,
we recompute \( f(a) \) in each if-test, but this is
not necessary if \( a \) has not changed since the last \( f(a) \) computations.
It is a good habit in numerical programming to avoid
redundant work.
On modern computers the Bisection algorithm normally runs so fast that
we can afford to do more work than necessary. However, if \( f(x) \) is not
a simple formula, but computed by comprehensive calculations in a
program, the evaluation of \( f \) might take minutes or even hours, and
reducing the number of evaluations in the Bisection algorithm is then
very important. We will therefore introduce extra variables in the
algorithm above to save an \( f(m) \) evaluation in each iteration in the
for loop:
f_a = f(a)
for i in range(0, n+1):
m = (a + b)/2
f_m = f(m)
if f_a*f_m <= 0:
b = m # root is in left half
else:
a = m # root is in right half
f_a = f_m
# f(x) has a root in [a,b]
To execute the algorithm above, we need to specify \( n \). Say we want to be sure that the root lies in an interval of maximum extent \( \epsilon \). After \( n \) iterations the length of our current interval is \( 2^{-n}(b-a) \), if \( [a,b] \) is the initial interval. The current interval is sufficiently small if $$ \begin{equation*} 2^{-n}(b-a) = \epsilon,\end{equation*} $$ which implies $$ \begin{equation} n = - {\ln\epsilon -\ln (b-a)\over\ln 2}\tp \tag{6} \end{equation} $$
Instead of calculating this \( n \), we may simply stop the iterations when
the length of the current interval is less than \( \epsilon \). The loop
is then naturally implemented as a while loop testing on
whether \( b-a \leq\epsilon \). To make the algorithm more foolproof,
we also insert a test to ensure that \( f(x) \) really changes sign
in the initial interval. This guarantees a root
in \( [a,b] \). (However, \( f(a)f(b) < 0 \) is not a necessary condition
if there is an even number of roots in the initial interval.)
Our final version of the Bisection algorithm now becomes
f_a=f(a)
if f_a*f(b) > 0:
# error: f does not change sign in [a,b]
i = 0
while b-a > epsilon:
i = i + 1
m = (a + b)/2
f_m = f(m)
if f_a*f_m <= 0:
b = m # root is in left half
else:
a = m # root is in right half
f_a = f_m
# if x is the real root, |x-m| < epsilon
A direct translation of the previous algorithm to a valid Python program is a matter of some minor edits:
eps = 1E-5
a, b = 0, 10
fa = f(a)
if fa*f(b) > 0:
print 'f(x) does not change sign in [%g,%g].' % (a, b)
sys.exit(1)
i = 0 # iteration counter
while b-a > eps:
i += 1
m = (a + b)/2.0
fm = f(m)
if fa*fm <= 0:
b = m # root is in left half of [a,b]
else:
a = m # root is in right half of [a,b]
fa = fm
print 'Iteration %d: interval=[%g, %g]' % (i, a, b)
x = m # this is the approximate root
print 'The root is', x, 'found in', i, 'iterations'
print 'f(%g)=%g' % (x, f(x))
To verify the implementation in bisection_v1.py we choose a very
simple \( f(x) \) where we know the exact root. One suitable example is a linear
function, \( f(x)=2x-3 \) such that \( x=3/2 \)
is the root of \( f \). As can be seen from the source code above,
we have inserted a print statement inside the
while loop to control that the program really does the right
things.
Running the program yields the output
Iteration 1: interval=[0, 5]
Iteration 2: interval=[0, 2.5]
Iteration 3: interval=[1.25, 2.5]
Iteration 4: interval=[1.25, 1.875]
...
Iteration 19: interval=[1.5, 1.50002]
Iteration 20: interval=[1.5, 1.50001]
The root is 1.50000572205 found in 20 iterations
f(1.50001)=1.14441e-05
The previous implementation of the bisection algorithm is fine for
many purposes. To solve a new problem \( f(x)=0 \) it is just necessary
to change the f(x) function in the program. However, if we
encounter solving \( f(x)=0 \) in another program in another context,
we must put the bisection algorithm into that program in the right
place. This is simple in practice, but it requires some careful work,
and it is easy to make errors. The task of solving \( f(x)=0 \) by
the bisection algorithm is much simpler and safer if we have that
algorithm available as a function in a module. Then we can just
import the function and call it. This requires a minimum of writing
in later programs.
When you have a "flat" program as shown above, without basic steps in the program collected in functions, you should always consider dividing the code into functions. The reason is that parts of the program will be much easier to reuse in other programs. You save coding, and that is a good rule! A program with functions is also easier to understand, because statements are collected into logical, separate units, which is another good rule! In a mathematical context, functions are particularly important since they naturally split the code into general algorithms (like the bisection algorithm) and a problem-specific part (like a special choice of \( f(x) \)).
Shuffling statements in a program around to form a new and better
designed version of the program is called refactoring.
We shall now refactor the bisection_v1.py program by putting
the statements in the bisection algorithm in a function
bisection. This function naturally takes \( f(x) \), \( a \), \( b \), and
\( \epsilon \) as parameters and returns the found root, perhaps together
with the number of iterations required:
def bisection(f, a, b, eps):
fa = f(a)
if fa*f(b) > 0:
return None, 0
i = 0 # iteration counter
while b-a > eps:
i += 1
m = (a + b)/2.0
fm = f(m)
if fa*fm <= 0:
b = m # root is in left half of [a,b]
else:
a = m # root is in right half of [a,b]
fa = fm
return m, i
def f(x):
return 2*x - 3 # one root x=1.5
x, iter = bisection(f, a=0, b=10, eps=1E-5)
if x is None:
print 'f(x) does not change sign in [%g,%g].' % (a, b)
else:
print 'The root is', x, 'found in', iter, 'iterations'
print 'f(%g)=%g' % (x, f(x))
Rather than having a main program as above for verifying the
implementation, we should make a test function test_bisection as
described in the section Verification of the module code. To this end, we
move the statements above inside a function, drop the output, but
instead make a boolean variable success that is True if the test
is passed and False otherwise. Then we do assert success, msg,
which will abort the program if the test fails. The msg variable is
a string with more explanation of what went wrong the test fails.
A test function with this structure is easy to integrate
into the widely used testing frameworks nose and pytest, and there are no good
reasons for not adopting this structure. The code checking that
the root is within a distance \( \epsilon \) to the exact root becomes
def test_bisection():
def f(x):
return 2*x - 3 # one root x=1.5
eps = 1E-5
x_expected = 1.5
x, iter = bisection(f, a=0, b=10, eps=eps)
success = abs(x - x_expected) < eps # test within eps tolerance
assert success, 'found x=%g != 1.5' % x
A motivating factor for implementing the bisection algorithm as a function
bisection was that we could import this function in other
programs to solve \( f(x)=0 \) equations. We therefore need to make a module
file bisection.py such that we can do, e.g.,
from bisection import bisection
x, iter = bisection(lambda x: x**3 + 2*x -1, -10, 10, 1E-5)
import statement will start executing
the main program, resulting in very
disturbing statements for another program that
wants to solve a different \( f(x)=0 \) equation.
The bisection_v2.py file had a main program that was just a
simple test for checking that the bisection algorithm works
for a linear function. We took this main program and wrapped
in a test function test_bisection above. To run the test,
we make the call to this function from the test block:
if __name__ == '__main__':
test_bisection()
bisection_v2.py
into a proper module file bisection.py.
It is nice to have our bisection module do more than just test
itself: there should be a user interface such that we can
solve real problems \( f(x)=0 \), where \( f(x) \), \( a \), \( b \), and \( \epsilon \)
are defined on the command line by the user. A dedicated function
can read from the command line and return the data as Python
object. For reading the function \( f(x) \) we can either apply
eval on the command-line argument, or use the more sophisticated
StringFunction tool from the section Turning string expressions into functions.
With eval we need to import functions from the math module in
case the user have such functions in the expression for \( f(x) \).
With StringFunction this is not necessary.
A get_input() for getting input from the command line can be
implemented as
def get_input():
"""Get f, a, b, eps from the command line."""
from scitools.std import StringFunction
try:
f = StringFunction(sys.argv[1])
a = float(sys.argv[2])
b = float(sys.argv[3])
eps = float(sys.argv[4])
except IndexError:
print 'Usage %s: f a b eps' % sys.argv[0]
sys.exit(1)
return f, a, b, eps
if test in the test block:
if __name__ == '__main__':
import sys
if len(sys.argv) >= 2 and sys.argv[1] == 'test':
test_bisection()
else:
f, a, b, eps = get_input()
x, iter = bisection(f, a, b, eps)
print 'Found root x=%g in %d iterations' % (x, iter)
Our bisection.py code is a complete module file with the following generally desired features of Python modules:
bisection function,
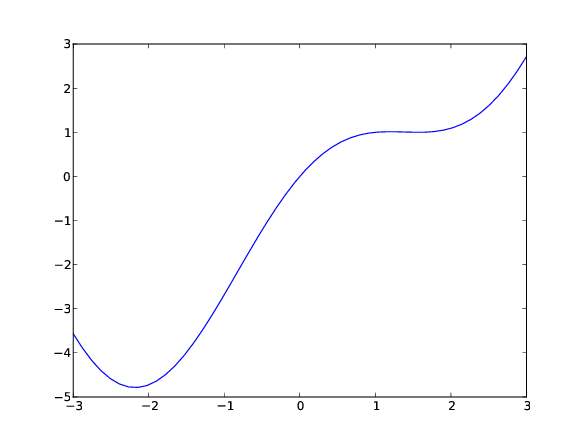
Suppose you want to solve \( x/(x-1)=\sin x \) using the bisection module.
What do you have to do? First, you must reformulate the equation as
\( f(x)=0 \), i.e., \( x/(x-1)-\sin x = 0 \), or maybe multiply by
\( x-1 \) to get \( f(x)=x-(x-1)\sin x \).
It is required to identify an interval for the root. By evaluating \( f(x) \)
for some points \( x \) one can be trial and error locate an interval.
A more convenient approach is to plot
the function \( f(x) \) and visually inspect where a root is.
We start ipython --pylab and write
In [1]: x = linspace(-3, 3, 50) # generate 50 coordinates in [-3,3]
In [2]: y = x - (x-1)*sin(x)
In [3]: plot(x, y)
Figure 3: Plot of \( f(x)=x - \sin (x) \).
The next step is to run the Bisection algorithm. There are two possibilities:
bisection function, orbisection.py program directly.
bisection.py "x - (x-1)*sin(x)" -2 1 1E-5
Found root x=-1.90735e-06 in 19 iterations
The alternative approach is to make a program:
from bisection import bisection
from math import sin
def f(x):
return x - (x-1)*sin(x)
x, iter = bisection(f, a=-2, b=1, eps=1E-5)
print x, iter
Let us solve
bisection.py "x-tanh(x)" -10 10
Found root x=-5.96046e-07 in 25 iterations
bisection.py "x**5-tanh(x**5)" -10 10
Found root x=-0.0266892 in 25 iterations
bisection_plot.py program
are 'x-tanh(x)' -1 1 and 'x**5-tanh(x**5)' -1 1.
The very flat area, in the latter case, where \( f(x)\approx 0 \) for
\( x\in [-1/2, 1/2] \) illustrates
well that it is difficult to locate an exact root.
The Python standard for installing software is to run a setup.py program,
Terminal> sudo python setup.py install
setup.py for the bisection
module arises from substituting the name interest by bisection
in the setup.py file listed in
the section Distributing modules. You can then distribute
bisection.py and setup.py together.