$$ \newcommand{\tp}{\thinspace .} $$

This chapter is taken from the book A Primer on Scientific Programming with Python by H. P. Langtangen, 5th edition, Springer, 2016.

Dictionaries

So far in the document we have stored information in various types of objects, such as numbers, strings, list, and arrays. A dictionary is a very flexible object for storing various kind of information, and in particular when reading files. It is therefore time to introduce the popular dictionary type.

A list is a collection of objects indexed by an integer going from 0 to the number of elements minus one. Instead of looking up an element through an integer index, it can be more handy to use a text. Roughly speaking, a list where the index can be a text is called a {dictionary} in Python. Other computer languages use other names for the same thing: HashMap, hash, associative array, or map.

Making dictionaries

Suppose we need to store the temperatures from three cities: Oslo, London, and Paris. For this purpose we can use a list,

temps = [13, 15.4, 17.5]

but then we need to remember the sequence of cities, e.g., that index 0 corresponds to Oslo, index 1 to London, and index 2 to Paris. That is, the London temperature is obtained as temps[1]. A dictionary with the city name as index is more convenient, because this allows us to write temps['London'] to look up the temperature in London. Such a dictionary is created by one of the following two statements

temps = {'Oslo': 13, 'London': 15.4, 'Paris': 17.5}
# or
temps = dict(Oslo=13, London=15.4, Paris=17.5)

Additional text-value pairs can be added when desired. We can, for instance, write

temps['Madrid'] = 26.0

The temps dictionary has now four text-value pairs, and a print temps yields

{'Oslo': 13, 'London': 15.4, 'Paris': 17.5, 'Madrid': 26.0}

Dictionary operations

The string "indices" in a dictionary are called keys. To loop over the keys in a dictionary d, one writes for key in d: and works with key and the corresponding value d[key] inside the loop. We may apply this technique to write out the temperatures in the temps dictionary from the previous paragraph:

>>> for city in temps:
...     print 'The temperature in %s is %g' % (city, temps[city])
...
The temperature in Paris is 17.5
The temperature in Oslo is 13
The temperature in London is 15.4
The temperature in Madrid is 26

We can check if a key is present in a dictionary by the syntax if key in d:

>>> if 'Berlin' in temps:
...     print 'Berlin:', temps['Berlin']
... else:
...     print 'No temperature data for Berlin'
...
No temperature data for Berlin

Writing key in d yields a standard boolean expression, e.g.,

>>> 'Oslo' in temps
True

The keys and values can be extracted as lists from a dictionary:

>>> temps.keys()
['Paris', 'Oslo', 'London', 'Madrid']
>>> temps.values()
[17.5, 13, 15.4, 26.0]

An important feature of the keys method in dictionaries is that the order of the returned list of keys is unpredictable. If you need to traverse the keys in a certain order, you can sort the keys. A loop over the keys in the temps dictionary in alphabetic order is written as

>>> for city in sorted(temps):
...     print city
...
London
Madrid
Oslo
Paris

Python also has a special dictionary type OrderedDict where the key-value pairs has a specific order, see the section Dictionaries with default values and ordering.

A key-value pair can be removed by del d[key]:

>>> del temps['Oslo']
>>> temps
{'Paris': 17.5, 'London': 15.4, 'Madrid': 26.0}
>>> len(temps)  # no of key-value pairs in dictionary
3

Sometimes we need to take a copy of a dictionary:

>>> temps_copy = temps.copy()
>>> del temps_copy['Paris']   # this does not affect temps
>>> temps_copy
{'London': 15.4, 'Madrid': 26.0}
>>> temps
{'Paris': 17.5, 'London': 15.4, 'Madrid': 26.0}

Note that if two variables refer to the same dictionary and we change the contents of the dictionary through either of the variables, the change will be seen in both variables:

>>> t1 = temps
>>> t1['Stockholm'] = 10.0    # change t1
>>> temps                     # temps is also changed
{'Stockholm': 10.0, 'Paris': 17.5, 'London': 15.4, 'Madrid': 26.0}

To avoid that temps is affected by adding a new key-value pair to t1, t1 must be a copy of temps.

Remark

In Python version 2.x, temps.keys() returns a list object while in Python version 3.x, temps.keys() only enables iterating over the keys. To write code that works with both versions one can use list(temps.keys()) in the cases where a list is really needed and just temps.keys() in a for loop over the keys.

Example: Polynomials as dictionaries

Python objects that cannot change their contents are known as immutable data types and consist of int, float, complex, str, and tuple. Lists and dictionaries can change their contents and are called mutable objects.

The keys in a dictionary are not restricted to be strings. In fact, any immutable Python object can be used as key. For example, if you want a list as key, it cannot be used since lists can change their contents are hence mutable objects, but a tuple will do, since it is immutable.

A common type of key in dictionaries is integers. Next we shall explain how dictionaries with integers as key provide a handy way of representing polynomials. Consider the polynomial $$ \begin{equation*} p(x)=-1 + x^2 + 3x^7\tp \end{equation*} $$ The data associated with this polynomial can be viewed as a set of power-coefficient pairs, in this case the coefficient $ -1 $ belongs to power 0, the coefficient 1 belongs to power 2, and the coefficient 3 belongs to power 7. A dictionary can be used to map a power to a coefficient:

p = {0: -1, 2: 1, 7: 3}

A list can, of course, also be used, but in this case we must fill in all the zero coefficients too, since the index must match the power:

p = [-1, 0, 1, 0, 0, 0, 0, 3]

The advantage with a dictionary is that we need to store only the non-zero coefficients. For the polynomial $ 1+x^{100} $ the dictionary holds two elements while the list holds 101 elements (see Exercise 10: Compare data structures for polynomials).

The following function can be used to evaluate a polynomial represented as a dictionary:

def eval_poly_dict(poly, x):
    sum = 0.0
    for power in poly:
        sum += poly[power]*x**power
    return sum

The poly argument must be a dictionary where poly[power] holds the coefficient associated with the term x**power.

A more compact implementation can make use of Python's sum function to sum the elements of a list:

def eval_poly_dict2(poly, x):
    return sum([poly[power]*x**power for power in poly])

That is, we first make a list of the terms in the polynomial using a list comprehension, and then we feed this list to the sum function. We can in fact drop the brackets and storing all the poly[power]*x**power numbers in a list, because sum can directly add elements of an iterator (like for power in poly):

def eval_poly_dict2(poly, x):
    return sum(poly[power]*x**power for power in poly)

Be careful with redefining variables!

The name sum appears in both eval_poly_dict and eval_poly_dict2. In the former, sum is a float object, and in the latter, sum is a built-in Python function. When we set sum=0.0 in the first implementation, we bind the name sum to a new float object, and the built-in Python function associated with the name sum is then no longer accessible inside the eval_poly_dict function. (Actually, this is not strictly correct, because sum is a local variable while the built-in Python sum function is associated with a global name sum, which can always be reached through globals()['sum'].) Outside the eval_poly_dict function, nevertheless, sum will be Python's summation function and the local sum variable inside the eval_poly_dict function is destroyed.

As a rule of thumb, avoid using sum or other names associated with frequently used functions as new variables unless you are in a very small function (like eval_poly_dict) where there is no danger that you need the original meaning of the name.

With a list instead of dictionary for representing the polynomial, a slightly different evaluation function is needed:

def eval_poly_list(poly, x):
    sum = 0
    for power in range(len(poly)):
        sum += poly[power]*x**power
    return sum

If there are many zeros in the poly list, eval_poly_list must perform all the multiplications with the zeros, while eval_poly_dict computes with the non-zero coefficients only and is hence more efficient.

Another major advantage of using a dictionary to represent a polynomial rather than a list is that negative powers are easily allowed, e.g.,

p = {-3: 0.5, 4: 2}

can represent $ \frac{1}{2}x^{-3} + 2x^4 $. With a list representation, negative powers require much more book-keeping. We may, for example, set

p = [0.5, 0, 0, 0, 0, 0, 0, 2]

and remember that p[i] is the coefficient associated with the power i-3. In particular, the eval_poly_list function will no longer work for such lists, while the eval_poly_dict function works also for dictionaries with negative keys (powers).

There is a dictionary counterpart to list comprehensions, called dictionary comprehensions, for quickly generating parameterized key-value pairs with a for loop. Such a construction is convenient to generate the coefficients in a polynomial:

from math import factorial
d = {k: (-1)**k/float(factorial(k)) for k in range(n+1)}

The d dictionary now contains the power-coefficient pairs of the Taylor polynomial of degree n for $ e^{-x} $. (Note the use of float to avoid integer division.)

You are now encouraged to solve Exercise 11: Compute the derivative of a polynomial to become more familiar with the concept of dictionaries.

Dictionaries with default values and ordering

Dictionaries with default values

Looking up keys that are not present in the dictionary requires special treatment. Consider a polynomial dictionary of the type introduced in the section Example: Polynomials as dictionaries. Say we have $ 2x^{-3} -1.5x^{-1} -2x^2 $ represented by

p1 = {-3: 2, -1: -1.5, 2: -2}

If the code tries to look up p1[1], this operation results in a KeyError since 1 is not a registered key in p1. We therefore need to do either

if key in p1:
   value = p1[key]

or use

value = p1.get(key, 0.0)

where p1.get returns p1[key] if key in p1 and the default value 0.0 if not. A third possibility is to work with a dictionary with a default value:

from collections import defaultdict

def polynomial_coeff_default():
    # default value for polynomial dictionary
    return 0.0

p2 = defaultdict(polynomial_coeff_default)
p2.update(p1)

The p2 can be indexed by any key, and for unregistered keys the polynomial_coeff_default function is called to provide a value. This must be a function without arguments. Usually, a separate function is never made, but either a type is inserted or a lambda function. The example above is equivalent to

p2 = defaultdict(lambda: 0.0)
p2 = defaultdict(float)

In the latter case float() is called for each unknown key, and float() returns a float object with zero value. Now we can look up p2[1] and get the default value 0. It must be remarked that this key is then a part of the dictionary:

>>> p2 = defaultdict(lambda: 0.0)
>>> p2.update({2: 8})  # only one key
>>> p2[1]
0.0
>>> p2[0]
0.0
>>> p2[-2]
0.0
>>> print p2
{0: 0.0, 1: 0.0, 2: 8, -2: 0.0}

Ordered dictionaries

The elements of a dictionary have an undefined order. For example,

>>> p1 = {-3: 2, -1: -1.5, 2: -2}
>>> print p1
{2: -2, -3: 2, -1: -1.5}

One can control the order by sorting the keys, either by the default sorting (alphabetically for string keys, ascending order for number keys):

>>> for key in sorted(p1):
...     print key, p1[key]
...
-3 2
-1 -1.5
2 -2

The sorted function also accept an optional argument where the user can supply a function that sorts two keys.

However, Python features a dictionary type that preserves the order of the keys as they were registered:

>>> from collections import OrderedDict
>>> p2 = OrderedDict({-3: 2, -1: -1.5, 2: -2})
>>> print p2
OrderedDict([(2, -2), (-3, 2), (-1, -1.5)])
>>> p2[-5] = 6
>>> for key in p2:
...     print key, p2[key]
...
2 -2
-3 2
-1 -1.5
-5 6

Here is an example with dates as keys where the order is important.

>>> data = {'Jan 2': 33, 'Jan 16': 0.1, 'Feb 2': 2}
>>> for date in data:
...     print date, data[date]
...
Feb 2 2
Jan 2 33
Jan 16 0.1

The order of the keys in the loop is not the right registered order, but this is easily achieved by OrderedDict

>>> data = OrderedDict()
>>> data['Jan 2'] = 33
>>> data['Jan 16'] = 0.1
>>> data['Feb 2'] = 2
>>> for date in data:
...     print date, data[date]
...
Jan2 33
Jan 16 0.1
Feb 2 2

A comment on alternative solutions should be made here. Trying to sort the data dictionary when it is an ordinary dict object does not help, as by default the sorting will be alphabetically, resulting in the sequence 'Feb 2', 'Jan 16', and 'Jan 2'. What does help, however, is to use Python's datetime objects as keys reflecting dates, since these objects will be correctly sorted. A datetime object can be created from a string like 'Jan 2, 2017' using a special syntax (see the module documentation). The relevant code is

>>> import datetime
>>> data = {}
>>> d = datetime.datetime.strptime  # short form
>>> data[d('Jan 2, 2017', '%b %d, %Y')] = 33
>>> data[d('Jan 16, 2017', '%b %d, %Y')] = 0.1
>>> data[d('Feb 2, 2017', '%b %d, %Y')] = 2

Printing out in sorted order gives the right sequence of dates:

>>> for date in sorted(data):
...     print date, data[date]
...
2017-01-02 00:00:00 33
2017-01-16 00:00:00 0.1
2017-02-02 00:00:00 2

The time is automatically part of a datetime object and set to 00:00:00 when not specified.

While OrderedDict provides a simpler and shorter solution to keeping keys (here dates) in the right order in a dictionary, using datetime objects for dates has many advantages: dates can be formatted and written out in various ways, counting days between two dates is easy, calculating the corresponding week number and name of the weekday is supported, to mention some functionality.

Example: Storing file data in dictionaries

Problem

The file files/densities.dat contains a table of densities of various substances measured in $ \hbox{g}/\hbox{cm}^3 $:

air         0.0012
gasoline    0.67
ice         0.9
pure water  1.0
seawater    1.025
human body  1.03
limestone   2.6
granite     2.7
iron        7.8
silver      10.5
mercury     13.6
gold        18.9
platinium   21.4
Earth mean  5.52
Earth core  13
Moon        3.3
Sun mean    1.4
Sun core    160
proton      2.3E+14

In a program we want to access these density data. A dictionary with the name of the substance as key and the corresponding density as value seems well suited for storing the data.

Solution

We can read the densities.dat file line by line, split each line into words, use a float conversion of the last word as density value, and the remaining one or two words as key in the dictionary.

def read_densities(filename):
    infile = open(filename, 'r')
    densities = {}
    for line in infile:
        words = line.split()
        density = float(words[-1])

        if len(words[:-1]) == 2:
            substance = words[0] + ' ' + words[1]
        else:
            substance = words[0]

        densities[substance] = density
    infile.close()
    return densities

densities = read_densities('densities.dat')

This code is found in the file density.py. With string operations from the section Common operations on strings we can avoid the special treatment of one or two words in the name of the substance and achieve simpler and more general code, see Exercise 3: Use string operations to improve a program.

Example: Storing file data in nested dictionaries

Problem

We are given a data file with measurements of some properties with given names (here A, B, C ...). Each property is measured a given number of times. The data are organized as a table where the rows contain the measurements and the columns represent the measured properties:

       A        B       C      D
1     11.7    0.035    2017    99.1
2      9.2    0.037    2019   101.2
3     12.2     no       no    105.2
4     10.1    0.031     no    102.1
5      9.1    0.033    2009   103.3
6      8.7    0.036    2015   101.9

The word no stands for no data, i.e., we lack a measurement. We want to read this table into a dictionary data so that we can look up measurement no. i of (say) property C as data['C'][i]. For each property p, we want to compute the mean of all measurements and store this as data[p]['mean'].

Algorithm

The algorithm for creating the data dictionary goes as follows:

examine the first line: split it into words and
initialize a dictionary with the property names
as keys and empty dictionaries {} as values

for each of the remaining lines in the file:
    split the line into words
    for each word after the first:
        if the word is not `no`:
            transform the word to a real number and store
            the number in the relevant dictionary

examine the first line: split it into words and initialize a dictionary with the property names as keys and empty dictionaries {} as values
for each of the remaining lines in the file

split the line into words
for each word after the first

if the word is not no:

transform the word to a real number and store the number in the relevant dictionary

Implementation

A new aspect needed in the solution is nested dictionaries, that is, dictionaries of dictionaries. The latter topic is first explained, via an example:

>>> d = {'key1': {'key1': 2, 'key2': 3}, 'key2': 7}

Observe here that the value of d['key1'] is a dictionary, which we can index with its keys key1 and key2:

>>> d['key1']            # this is a dictionary
{'key2': 3, 'key1': 2}
>>> type(d['key1'])      # proof
<type 'dict'>
>>> d['key1']['key1']    # index a nested dictionary
2
>>> d['key1']['key2']
3

In other words, repeated indexing works for nested dictionaries as for nested lists. The repeated indexing does not apply to d['key2'] since that value is just an integer:

>>> d['key2']['key1']
  ...
TypeError: unsubscriptable object
>>> type(d['key2'])
<type 'int'>

When we have understood the concept of nested dictionaries, we are in a position to present a complete code that solves our problem of loading the tabular data in the file table.dat into a nested dictionary data and computing mean values. First, we list the program, stored in the file table2dict.py, and display the program's output. Thereafter, we dissect the code in detail.

infile = open('table.dat', 'r')
lines = infile.readlines()
infile.close()
data = {}   #  data[property][measurement_no] = propertyvalue
first_line = lines[0]
properties = first_line.split()
for p in properties:
    data[p] = {}

for line in lines[1:]:
    words = line.split()
    i = int(words[0])       # measurement number
    values = words[1:]      # values of properties
    for p, v in zip(properties, values):
        if v != 'no':
            data[p][i] = float(v)

# Compute mean values
for p in data:
    values = data[p].values()
    data[p]['mean'] = sum(values)/len(values)

for p in sorted(data):
    print 'Mean value of property %s = %g' % (p, data[p]['mean'])

The corresponding output from this program becomes

Mean value of property A = 10.1667
Mean value of property B = 0.0344
Mean value of property C = 2015
Mean value of property D = 102.133

To view the nested data dictionary, we may insert

import scitools.pprint2; scitools.pprint2.pprint(data)

which produces something like

{'A': {1: 11.7, 2: 9.2, 3: 12.2, 4: 10.1, 5: 9.1, 6: 8.7,
       'mean': 10.1667},
 'B': {1: 0.035, 2: 0.037, 4: 0.031, 5: 0.033, 6: 0.036,
       'mean': 0.0344},
 'C': {1: 2017, 2: 2019, 5: 2009, 6: 2015, 'mean': 2015},
 'D': {1: 99.1,
       2: 101.2,
       3: 105.2,
       4: 102.1,
       5: 103.3,
       6: 101.9,
       'mean': 102.133}}

Dissection

To understand a computer program, you need to understand what the result of every statement is. Let us work through the code, almost line by line, and see what it does.

First, we load all the lines of the file into a list of strings called lines. The first_line variable refers to the string

'       A        B       C      D'

We split this line into a list of words, called properties, which then contains

['A', 'B', 'C', 'D']

With each of these property names we associate a dictionary with the measurement number as key and the property value as value, but first we must create these "inner" dictionaries as empty before we can add the measurements:

for p in properties:
    data[p] = {}

The first pass in the for loop picks out the string

'1     11.7    0.035    2017    99.1'

as the line variable. We split this line into words, the first word (words[0]) is the measurement number, while the rest words[1:] is a list of property values, here named values. To pair up the right properties and values, we loop over the properties and values lists simultaneously:

    for p, v in zip(properties, values):
        if v != 'no':
            data[p][i] = float(v)

Recall that some values may be missing and we drop to record that value (we could, alternatively, set the value to None). Because the values list contains strings (words) read from the file, we need to explicitly transform each string to a float number before we can compute with the values.

Figure 1: Illustration of the nested dictionary created in the table2dict.py program.

After the for line in lines[1:] loop, we have a dictionary data of dictionaries where all the property values are stored for each measurement number and property name. Figure 1 shows a graphical representation of the data dictionary.

It remains to compute the average values. For each property name p, i.e., key in the data dictionary, we can extract the recorded values as the list data[p].values() and simply send this list to Python's sum function and divide by the number of measured values for this property, i.e., the length of the list:

for p in data:
    values = data[p].values()
    data[p]['mean'] = sum(values)/len(values)

Alternatively, we can write an explicit loop to compute the average:

for p in data:
    sum_values = 0
    for value in data[p]:
        sum_values += value
    data[p]['mean'] = sum_values/len(data[p])

When we want to look up a measurement no. n of property B, we must recall that this particular measurement may be missing so we must do a test if n is key in the dictionary data[p]:

if n in data['B']:
    value = data['B'][n]

# alternative:
value = data['B'][n] if n in data['B'] else None

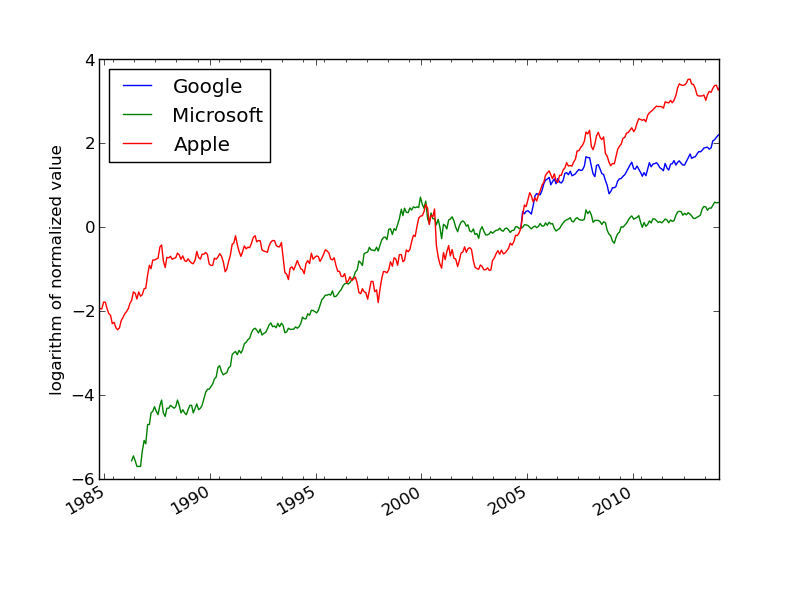
Example: Reading and plotting data recorded at specific dates

Problem

We want to compare the evolution of the stock prices of some giant companies in the computer industry: Microsoft, Apple, and Google. Relevant data files for stock prices can be downloaded from http://finance.yahoo.com. Fill in the company's name and click on Search Finance in the top bar of this page and choose Historical Prices in the left pane. On the resulting web page one can specify start and end dates for the historical prices of the stock. The default values were used in this example. Ticking off Monthly values and clicking Get Prices result in a table of stock prices for each month since the stock was introduced. The table can be downloaded as a spreadsheet file in CSV format, typically looking like

Date,Open,High,Low,Close,Volume,Adj Close
2014-02-03,502.61,551.19,499.30,545.99,12244400,545.99
2014-01-02,555.68,560.20,493.55,500.60,15698500,497.62
2013-12-02,558.00,575.14,538.80,561.02,12382100,557.68
2013-11-01,524.02,558.33,512.38,556.07,9898700,552.76
2013-10-01,478.45,539.25,478.28,522.70,12598400,516.57
...
1984-11-01,25.00,26.50,21.87,24.75,5935500,2.71
1984-10-01,25.00,27.37,22.50,24.87,5654600,2.73
1984-09-07,26.50,29.00,24.62,25.12,5328800,2.76

The file format is simple: columns are separated by comma, the first line contains column headings, and the data lines have the date in the first column and various measures of stock prices in the next columns. Reading about the meaning of the various data on the Yahoo! web pages reveals that our interest concerns the final column (as these prices are adjusted for splits and dividends). Three relevant data files can be found in the folder src/files with the names stockprices_X.csv, where X is Microsoft, Apple, or Google.

The task is visually illustrate the historical, relative stock market value of these companies. For this purpose it is natural to scale the prices of a company's stock to start at a unit value when the most recent company entered the market. Since the date of entry varies, the oldest data point can be skipped such that all data points correspond to the first trade day every month.

Solution

There are two major parts of this problem: reading the file and plotting the data. The reading part is quite straightforward, while the plotting part needs some special considerations since the $ x $ values in the plot are dates and not real numbers. In the forthcoming text we solve the individual subproblems one by one, showing the relevant Python snippets. The complete program is found in the file stockprices.py.

We start with the reading part. Since the reading will be repeated for several companies, we create a function for extracting the relevant data for a specific company. These data cover the dates in column 1 and the stock prices in the last column. Since we want to plot prices versus dates, it will be convenient to turn the dates into date objects. In more detail the algorithms has the following points:

open the file
create two empty lists, dates and prices, for collecting the data
read the first line (of no interest)
for each line in the rest of the file:
1. split the line wrt. comma into words
2. append the first word to the dates list
3. append the last word to the prices list
reverse the lists (oldest date first)
convert date strings to datetime objects
convert prices list to float array for computations
return dates and prices, except for the first (oldest) data point

There are a couple of additional points to consider. First, the words on a line are strings, and at least the prices (last word) should be converted to a float. Second, the recipe for converting dates like '2008-02-04' to date (or datetime) objects goes as

from datetime import datetime
datefmt = '%Y-%m-%d'  # date format YYYY-MM-DD used in datetime
strdate = '2008-02-04'
datetime_object = datetime.strptime(strdate, datefmt)
date_object = datetime_object.date()

The nice thing with date and datetime object is that we can compute with them and in particular used them in plotting with Matplotlib.

We can now translate the algorithm to Python code:

from datetime import datetime

def read_file(filename):
    infile = open(filename, 'r')
    infile.readline()  # read column headings
    dates = [];  prices = []
    for line in infile:
        words = line.split(',')
        dates.append(words[0])
        prices.append(float(words[-1]))
    infile.close()
    dates.reverse()
    prices.reverse()
    # Convert dates on the form 'YYYY-MM-DD' to date objects
    datefmt = '%Y-%m-%d'
    dates = [datetime.strptime(_date, datefmt).date()
             for _date in dates]
    prices = np.array(prices)
    return dates[1:], prices[1:]

Although we work with three companies in this example, it is easy and almost always a good idea to generalize the program to an arbitrary number of companies. All we assume is that their stock prices are in files with names of the form stockprices_X.csv, where X is the company name. With aid of the function call glob.glob('stockprices_*.csv') we get a list of all such files. By looping over this list, extracting the company name, and calling read_file, we can store the dates and corresponding prices in dictionaries dates and prices, indexed by the company name:

dates = {};  prices = {}
import glob, numpy as np
filenames = glob.glob('stockprices_*.csv')
companies = []
for filename in filenames:
    company = filename[12:-4]
    d, p = read_file(filename)
    dates[company] = d
    prices[company] = p

The next step is to normalize the prices such that they coincide on a certain date. We pick this date as the first month we have data for the youngest company. In lists of date or datetime objects, we can use Python's max and min functions to extract the newest and oldest date.

first_months = [dates[company][0] for company in dates]
normalize_date = max(first_months)
for company in dates:
    index = dates[company].index(normalize_date)
    prices[company] /= prices[company][index]

# Plot log of price versus years

import matplotlib.pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator, DateFormatter

fig, ax = plt.subplots()
legends = []
for company in prices:
    ax.plot_date(dates[company], np.log(prices[company]),
                 '-', label=company)
    legends.append(company)
ax.legend(legends, loc='upper left')
ax.set_ylabel('logarithm of normalized value')

# Format the ticks
years    = YearLocator(5)   # major ticks every 5 years
months   = MonthLocator(6)  # minor ticks every 6 months
yearsfmt = DateFormatter('%Y')
ax.xaxis.set_major_locator(years)
ax.xaxis.set_major_formatter(yearsfmt)
ax.xaxis.set_minor_locator(months)
ax.autoscale_view()
fig.autofmt_xdate()

plt.savefig('tmp.pdf'); plt.savefig('tmp.png')
plt.show()

The normalized prices vary a lot, so to see the development over 30 years better, we decide to take the logarithm of the prices. The plotting procedure is somewhat involved so the reader should take the coming code more as a recipe than as a sequence of statement to really understand:

import matplotlib.pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator, DateFormatter

fig, ax = plt.subplots()
legends = []
for company in prices:
    ax.plot_date(dates[company], np.log(prices[company]),
                 '-', label=company)
    legends.append(company)
ax.legend(legends, loc='upper left')
ax.set_ylabel('logarithm of normalized value')

# Format the ticks
years    = YearLocator(5)   # major ticks every 5 years
months   = MonthLocator(6)  # minor ticks every 6 months
yearsfmt = DateFormatter('%Y')
ax.xaxis.set_major_locator(years)
ax.xaxis.set_major_formatter(yearsfmt)
ax.xaxis.set_minor_locator(months)
ax.autoscale_view()
fig.autofmt_xdate()

plt.savefig('tmp.pdf'); plt.savefig('tmp.png')

Figure 2 shows the resulting plot. We observe that the normalized prices coincide when Google entered the market, here at Sep 1, 2004. Note that there is a log scale on the vertical axis. You may want to plot the real normalized prices to get a stronger impression of the significant recent rise in value, especially for Apple.

Figure 2: The evolution of stock prices for three companies.

« Previous

Next »