A very wide range of physical processes lead to wave motion, where signals are propagated through a medium in space and time, normally with little or no permanent movement of the medium itself. The shape of the signals may undergo changes as they travel through matter, but usually not so much that the signals cannot be recognized at some later point in space and time. Many types of wave motion can be described by the equation $ u_{tt}=\nabla\cdot (c^2\nabla u) + f $, which we will solve in the forthcoming text by finite difference methods.

Simulation of waves on a string

We begin our study of wave equations by simulating one-dimensional waves on a string, say on a guitar or violin. Let the string in the deformed state coincide with the interval $ [0,L] $ on the $ x $ axis, and let $ u(x,t) $ be the displacement at time $ t $ in the $ y $ direction of a point initially at $ x $. The displacement function $ u $ is governed by the mathematical model $$ \begin{align} \frac{\partial^2 u}{\partial t^2} &= c^2 \frac{\partial^2 u}{\partial x^2}, \quad &x\in (0,L),\ t\in (0,T] \tag{1}\\ u(x,0) &= I(x), \quad &x\in [0,L] \tag{2}\\ \frac{\partial}{\partial t}u(x,0) &= 0, \quad &x\in [0,L] \tag{3}\\ u(0,t) & = 0, \quad &t\in (0,T] \tag{4}\\ u(L,t) & = 0, \quad &t\in (0,T] \tag{5} \end{align} $$ The constant $ c $ and the function $ I(x) $ must be prescribed.

Equation (1) is known as the one-dimensional wave equation. Since this PDE contains a second-order derivative in time, we need two initial conditions. The condition (2) specifies the initial shape of the string, $ I(x) $, and (3) expresses that the initial velocity of the string is zero. In addition, PDEs need boundary conditions, give here as (4) and (5). These two conditions specify that the string is fixed at the ends, i.e., that the displacement $ u $ is zero.

The solution $ u(x,t) $ varies in space and time and describes waves that move with velocity $ c $ to the left and right.

Example of waves on a string.

Sometimes we will use a more compact notation for the partial derivatives to save space: $$ \begin{equation} u_t = \frac{\partial u}{\partial t}, \quad u_{tt} = \frac{\partial^2 u}{\partial t^2}, \tag{6} \end{equation} $$ and similar expressions for derivatives with respect to other variables. Then the wave equation can be written compactly as $ u_{tt} = c^2u_{xx} $.

The PDE problem (1)-(5) will now be discretized in space and time by a finite difference method.

Discretizing the domain

The temporal domain $ [0,T] $ is represented by a finite number of mesh points $$ \begin{equation} 0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T \tp \tag{7} \end{equation} $$ Similarly, the spatial domain $ [0,L] $ is replaced by a set of mesh points $$ \begin{equation} 0 = x_0 < x_1 < x_2 < \cdots < x_{N_x-1} < x_{N_x} = L \tp \tag{8} \end{equation} $$ One may view the mesh as two-dimensional in the $ x,t $ plane, consisting of points $ (x_i, t_n) $, with $ i=0,\ldots,N_x $ and $ n=0,\ldots,N_t $.

Uniform meshes

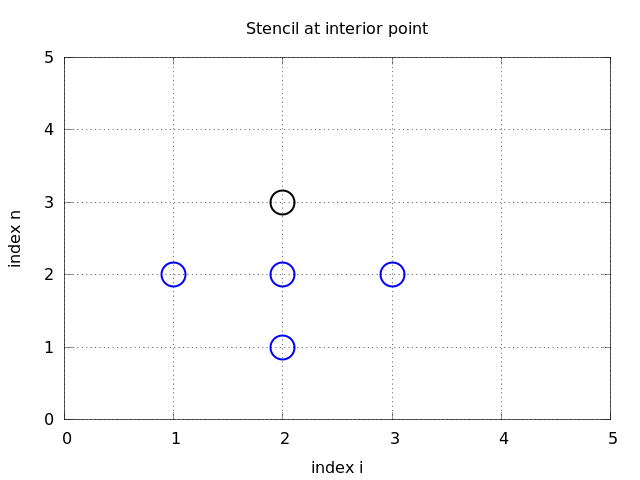
For uniformly distributed mesh points we can introduce the constant mesh spacings $ \Delta t $ and $ \Delta x $. We have that $$ \begin{equation} x_i = i\Delta x,\ i=0,\ldots,N_x,\quad t_n = n\Delta t,\ n=0,\ldots,N_t\tp \tag{9} \end{equation} $$ We also have that $ \Delta x = x_i-x_{i-1} $, $ i=1,\ldots,N_x $, and $ \Delta t = t_n - t_{n-1} $, $ n=1,\ldots,N_t $. Figure 1 displays a mesh in the $ x,t $ plane with $ N_t=5 $, $ N_x=5 $, and constant mesh spacings.

The discrete solution

The solution $ u(x,t) $ is sought at the mesh points. We introduce the mesh function $ u_i^n $, which approximates the exact solution at the mesh point $ (x_i,t_n) $ for $ i=0,\ldots,N_x $ and $ n=0,\ldots,N_t $. Using the finite difference method, we shall develop algebraic equations for computing the mesh function.

Fulfilling the equation at the mesh points

In the finite difference method, we relax the condition that (1) holds at all points in the space-time domain $ (0,L)\times (0,T] $ to the requirement that the PDE is fulfilled at the interior mesh points only: $$ \begin{equation} \frac{\partial^2}{\partial t^2} u(x_i, t_n) = c^2\frac{\partial^2}{\partial x^2} u(x_i, t_n), \tag{10} \end{equation} $$ for $ i=1,\ldots,N_x-1 $ and $ n=1,\ldots,N_t-1 $. For $ n=0 $ we have the initial conditions $ u=I(x) $ and $ u_t=0 $, and at the boundaries $ i=0,N_x $ we have the boundary condition $ u=0 $.

Replacing derivatives by finite differences

The second-order derivatives can be replaced by central differences. The most widely used difference approximation of the second-order derivative is $$ \frac{\partial^2}{\partial t^2}u(x_i,t_n)\approx \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2}\tp$$ It is convenient to introduce the finite difference operator notation $$ [D_tD_t u]^n_i = \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2}\tp$$ A similar approximation of the second-order derivative in the $ x $ direction reads $$ \frac{\partial^2}{\partial x^2}u(x_i,t_n)\approx \frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2} = [D_xD_x u]^n_i \tp $$

Algebraic version of the PDE

We can now replace the derivatives in (10) and get $$ \begin{equation} \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2} = c^2\frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2}, \tag{11} \end{equation} $$ or written more compactly using the operator notation: $$ \begin{equation} [D_tD_t u = c^2 D_xD_x]^{n}_i \tp \tag{12} \end{equation} $$

Interpretation of the equation as a stencil

A typical feature of (11) is that it involves $ u $ values from neighboring points only: $ u_i^{n+1} $, $ u^n_{i\pm 1} $, $ u^n_i $, and $ u^{n-1}_i $. The circles in Figure 1 illustrate such neighboring mesh points that contributes to an algebraic equation. In this particular case, we have sampled the PDE at the point $ (2,2) $ and constructed (11), which then involves a coupling of $ u_2^1 $, $ u_1^2 $, $ u_2^2 $, $ u_3^2 $, and $ u_2^3 $. The term stencil is often used about the algebraic equation at a mesh point, and the geometry of a typical stencil is illustrated in Figure 1. One also often refers to the algebraic equations as discrete equations, (finite) difference equations or a finite difference scheme.

Figure 1: Mesh in space and time. The circles show points connected in a finite difference equation.

Algebraic version of the initial conditions

We also need to replace the derivative in the initial condition (3) by a finite difference approximation. A centered difference of the type $$ \frac{\partial}{\partial t} u(x_i,t_n)\approx \frac{u^1_i - u^{-1}_i}{2\Delta t} = [D_{2t} u]^0_i, $$ seems appropriate. In operator notation the initial condition is written as $$ [D_{2t} u]^n_i = 0,\quad n=0 \tp $$ Writing out this equation and ordering the terms give $$ \begin{equation} u^{n-1}_i=u^{n+1}_i,\quad i=0,\ldots,N_x,\ n=0\tp \tag{13} \end{equation} $$ The other initial condition can be computed by $$ u_i^0 = I(x_i),\quad i=0,\ldots,N_x\tp$$

Formulating a recursive algorithm

We assume that $ u^n_i $ and $ u^{n-1}_i $ are already computed for $ i=0,\ldots,N_x $. The only unknown quantity in (11) is therefore $ u^{n+1}_i $, which we can solve for: $$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right), \tag{14} \end{equation} $$ where we have introduced the parameter $$ \begin{equation} C = c\frac{\Delta t}{\Delta x}, \tag{15} \end{equation} $$ known as the Courant number.

$ C $ is the key parameter in the discrete wave equation. We see that the discrete version of the PDE features only one parameter, $ C $, which is therefore the key parameter that governs the quality of the numerical solution (see the section Analysis of the difference equations for details). Both the primary physical parameter $ c $ and the numerical parameters $ \Delta x $ and $ \Delta t $ are lumped together in $ C $. Note that $ C $ is a dimensionless parameter.

Given that $ u^{n-1}_i $ and $ u^n_i $ are computed for $ i=0,\ldots,N_x $, we find new values at the next time level by applying the formula (14) for $ i=1,\ldots,N_x-1 $. Figure 1 illustrates the points that are used to compute $ u^3_2 $. For the boundary points, $ i=0 $ and $ i=N_x $, we apply the boundary conditions $ u_i^{n+1}=0 $.

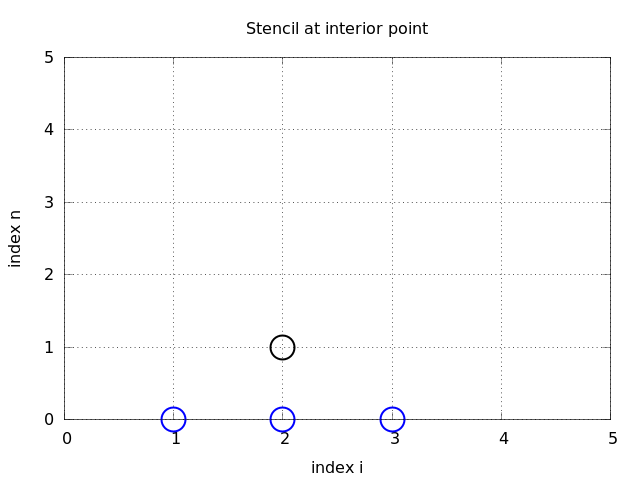
A problem with (14) arises when $ n=0 $ since the formula for $ u^1_i $ involves $ u^{-1}_i $, which is an undefined quantity outside the time mesh (and the time domain). However, we can use the initial condition (13) in combination with (14) when $ n=0 $ to eliminate $ u^{-1}_i $ and arrive at a special formula for $ u_i^1 $: $$ \begin{equation} u_i^1 = u^0_i - \half C^2\left(u^{0}_{i+1}-2u^{0}_{i} + u^{0}_{i-1}\right) \tp \tag{16} \end{equation} $$ Figure 2 illustrates how (16) connects four instead of five points: $ u^1_2 $, $ u_1^0 $, $ u_2^0 $, and $ u_3^0 $.

Figure 2: Modified stencil for the first time step.

We can now summarize the computational algorithm:

Compute $ u^0_i=I(x_i) $ for $ i=0,\ldots,N_x $
Compute $ u^1_i $ by (16) and set $ u_i^1=0 $ for the boundary points $ i=0 $ and $ i=N_x $, for $ n=1,2,\ldots,N-1 $,
For each time level $ n=1,2,\ldots,N_t-1 $
1. apply (14) to find $ u^{n+1}_i $ for $ i=1,\ldots,N_x-1 $
2. set $ u^{n+1}_i=0 $ for the boundary points $ i=0 $, $ i=N_x $.

The algorithm essentially consists of moving a finite difference stencil through all the mesh points, which can be seen as an animation in a web page or a movie file.

Sketch of an implementation

In a Python implementation of this algorithm, we use the array elements u[i] to store $ u^{n+1}_i $, u_1[i] to store $ u^n_i $, and u_2[i] to store $ u^{n-1}_i $. Our naming convention is use u for the unknown new spatial field to be computed, u_1 as the solution at one time step back in time, u_2 as the solution two time steps back in time and so forth.

The algorithm only involves the three most recent time levels, so we need only three arrays for $ u_i^{n+1} $, $ u_i^n $, and $ u_i^{n-1} $, $ i=0,\ldots,N_x $. Storing all the solutions in a two-dimensional array of size $ (N_x+1)\times (N_t+1) $ would be possible in this simple one-dimensional PDE problem, but is normally out of the question in three-dimensional (3D) and large two-dimensional (2D) problems. We shall therefore, in all our PDE solving programs, have the unknown in memory at as few time levels as possible.

The following Python snippet realizes the steps in the computational algorithm.

# Given mesh points as arrays x and t (x[i], t[n])
dx = x[1] - x[0]
dt = t[1] - t[0]
C = c*dt/dx            # Courant number
Nt = len(t)-1
C2 = C**2              # Help variable in the scheme

# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
    u_1[i] = I(x[i])

# Apply special formula for first step, incorporating du/dt=0
for i in range(1, Nx):
    u[i] = u_1[i] - 0.5*C**2(u_1[i+1] - 2*u_1[i] + u_1[i-1])
u[0] = 0;  u[Nx] = 0   # Enforce boundary conditions

# Switch variables before next step
u_2[:], u_1[:] = u_1, u

for n in range(1, Nt):
    # Update all inner mesh points at time t[n+1]
    for i in range(1, Nx):
        u[i] = 2u_1[i] - u_2[i] - \ 
               C**2(u_1[i+1] - 2*u_1[i] + u_1[i-1])

    # Insert boundary conditions
    u[0] = 0;  u[Nx] = 0

    # Switch variables before next step
    u_2[:], u_1[:] = u_1, u

Verification

Before implementing the algorithm, it is convenient to add a source term to the PDE (1) since it gives us more freedom in finding test problems for verification. Physically, a source term acts as a generation of waves in the interior of the domain.

A slightly generalized model problem

We now address the following extended initial-boundary value problem for one-dimensional wave phenomena: $$ \begin{align} u_{tt} &= c^2 u_{xx} + f(x,t), \quad &x\in (0,L),\ t\in (0,T] \tag{17}\\ u(x,0) &= I(x), \quad &x\in [0,L] \tag{18}\\ u_t(x,0) &= V(x), \quad &x\in [0,L] \tag{19}\\ u(0,t) & = 0, \quad &t>0 \tag{20}\\ u(L,t) & = 0, \quad &t>0 \tag{21} \end{align} $$

Sampling the PDE at $ (x_i,t_n) $ and using the same finite difference approximations as above, yields $$ \begin{equation} [D_tD_t u = c^2 D_xD_x u + f]^{n}_i \tp \tag{22} \end{equation} $$ Writing this out and solving for the unknown $ u^{n+1}_i $ results in $$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2 (u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}) + \Delta t^2 f^n_i \tag{23} \tp \end{equation} $$

The equation for the first time step must be rederived. The discretization of the initial condition $ u_t = V(x) $ at $ t=0 $ becomes $$ [D_{2t}u = V]^0_i\quad\Rightarrow\quad u^{-1}_i = u^{1}_i - 2\Delta t V_i,$$ which, when inserted in (23) for $ n=0 $, gives the special formula $$ \begin{equation} u^{1}_i = u^0_i - \Delta t V_i + {\half} C^2 \left(u^{0}_{i+1}-2u^{0}_{i} + u^{0}_{i-1}\right) + \half\Delta t^2 f^0_i \tag{24} \tp \end{equation} $$

Using an analytical solution of physical significance

Many wave problems feature sinusoidal oscillations in time and space. For example, the original PDE problem (1)-(5) allows an exact solution $$ \begin{equation} \uex(x,t)) = A\sin\left(\frac{\pi}{L}x\right) \cos\left(\frac{\pi}{L}ct\right)\tp \tag{25} \end{equation} $$ This $ \uex $ fulfills the PDE with $ f=0 $, boundary conditions $ \uex(0,t)=\uex(L,0)=0 $, as well as initial conditions $ I(x)=A\sin\left(\frac{\pi}{L}x\right) $ and $ V=0 $.

It is common to use such exact solutions of physical interest to verify implementations. However, the numerical solution $ u^n_i $ will only be an approximation to $ \uex(x_i,t_n) $. We have no knowledge of the precise size of the error in this approximation, and therefore we can never know if discrepancies between $ u^n_i $ and $ \uex(x_i,t_n) $ are caused by mathematical approximations or programming errors. In particular, if a plot of the computed solution $ u^n_i $ and the exact one (25) looks similar, many are tempted to claim that the implementation works. However, even if color plots look nice and the accuracy is "deemed good", there can still be serious programming errors present!

The only way to use exact physical solutions like (25) for serious and thorough verification is to run a series of finer and finer meshes, measure the integrated error in each mesh, and from this information estimate the empirical convergence rate of the method. An introduction to the computing convergence rates is given in the section on convergence rates in [1].

In the present problem, one expects the method to have a convergence rate of 2 (see the section Analysis of the difference equations), so if the computed rates are close to 2 on a sufficiently mesh, we have good evidence that the implementation is free of programming mistakes.

Manufactured solution

One problem with the exact solution (25) is that it requires a simplification ($ V=0, f=0 $) of the implemented problem (17)-(21). An advantage of using a manufactured solution is that we can test all terms in the PDE problem. The idea of this approach is to set up some chosen solution and fit the source term, boundary conditions, and initial conditions to be compatible with the chosen solution. Given that our boundary conditions in the implementation are $ u(0,t)=u(L,t)=0 $, we must choose a solution that fulfills these conditions. One example is $$ \uex(x,t) = x(L-x)\sin t\tp$$ Inserted in the PDE $ u_{tt}=c^2u_{xx}+f $ we get $$ -x(L-x)\sin t = -c^2 2\sin t + f\quad\Rightarrow f = (2c^2 - x(L-x))\sin t\tp$$ The initial conditions become $$ \begin{align*} u(x,0) =& I(x) = 0,\\ u_t(x,0) &= V(x) = x(L-x)\tp \end{align*} $$

To verify the code, we compute the convergence rates in a series of simulations, letting each simulation use a finer mesh than the previous one. Such empirical estimation of convergence rates tests rely on an assumption that some measure $ E $ of the numerical error is related to the discretization parameters through $$ E = C_t\Delta t^r + C_x\Delta x^p,$$ where $ C_t $, $ C_x $, $ r $, and $ p $ are constants. The constants $ r $ and $ p $ are known as the convergence rates in time and space, respectively. From the accuracy in the finite difference approximations, we expect $ r=p=2 $, since the error terms are of order $ \Delta t^2 $ and $ \Delta x^2 $. This is confirmed by truncation error analysis and other types of analysis.

By using an exact solution of the PDE problem, we will next compute the error measure $ E $ on a sequence of refined meshes and see if the rates $ r=p=2 $ are obtained. We will not be concerned with estimating the constants $ C_t $ and $ C_x $.

It is advantageous to introduce a single discretization parameter $ h=\Delta t=\hat c \Delta x $ for some constant $ \hat c $. Since $ \Delta t $ and $ \Delta x $ are related through the Courant number, $ \Delta t = C\Delta x/c $, we set $ h=\Delta t $, and then $ \Delta x = hc/C $. Now the expression for the error measure is greatly simplified: $$ E = C_t\Delta t^r + C_x\Delta x^r = C_t h^r + C_x\left(\frac{c}{C}\right)^r h^r = Dh^r,\quad D = C_t+C_x\left(\frac{c}{C}\right)^r \tp$$

We choose an initial discretization parameter $ h_0 $ and run experiments with decreasing $ h $: $ h_i=2^{-i}h_0 $, $ i=1,2,\ldots,m $. Halving $ h $ in each experiment is not necessary, but it is a common choice. For each experiment we must record $ E $ and $ h $. A standard choice of error measure is the $ \ell^2 $ or $ \ell^\infty $ norm of the error mesh function $ e^n_i $: $$ \begin{align} E &= ||e^n_i||_{\ell^2} = \left( \Delta t\Delta x \sum_{n=0}^{N_t}\sum_{i=0}^{N_x} (e^n_i)^2\right)^{\half},\quad e^n_i = \uex(x_i,t_n)-u^n_i, \tag{26}\\ E &= ||e^n_i||_{\ell^\infty} = \max_{i,n} |e^i_n|\tp \tag{27} \end{align} $$ In Python, one can compute $ \sum_{i}(e^{n}_i)^2 $ at each time step and accumulate the value in some sum variable, say e2_sum. At the final time step one can do sqrt(dt*dx*e2_sum). For the $ \ell^\infty $ norm one must compare the maximum error at a time level (e.max()) with the global maximum over the time domain: e_max = max(e_max, e.max()).

An alternative error measure is to use a spatial norm at one time step only, e.g., the end time $ T $ ($ n=N_t $): $$ \begin{align} E &= ||e^n_i||_{\ell^2} = \left( \Delta x\sum_{i=0}^{N_x} (e^n_i)^2\right)^{\half},\quad e^n_i = \uex(x_i,t_n)-u^n_i, \tag{28}\\ E &= ||e^n_i||_{\ell^\infty} = \max_{0\leq i\leq N_x} |e^{n}_i|\tp \tag{29} \end{align} $$ The important issue is that our error measure $ E $ must be one number that represents the error in the simulation.

Let $ E_i $ be the error measure in experiment (mesh) number $ i $ and let $ h_i $ be the corresponding discretization parameter ($ h $). With the error model $ E_i = Dh_i^r $, we can estimate $ r $ by comparing two consecutive experiments: $$ \begin{align*} E_{i+1}& =D h_{i+1}^{r},\\ E_{i}& =D h_{i}^{r}\tp \end{align*} $$ Dividing the two equations eliminates the (uninteresting) constant $ D $. Thereafter, solving for $ r $ yields $$ r = \frac{\ln E_{i+1}/E_{i}}{\ln h_{i+1}/h_{i}}\tp $$ Since $ r $ depends on $ i $, i.e., which simulations we compare, we add an index to $ r $: $ r_i $, where $ i=0,\ldots,m-2 $, if we have $ m $ experiments: $ (h_0,E_0),\ldots,(h_{m-1}, E_{m-1}) $.

In our present discretization of the wave equation we expect $ r=2 $, and hence the $ r_i $ values should converge to 2 as $ i $ increases.

Constructing an exact solution of the discrete equations

With a manufactured or known analytical solution, as outlined above, we can estimate convergence rates and see if they have the correct asymptotic behavior. Experience shows that this is a quite good verification technique in that many common bugs will destroy the convergence rates. A significantly better test though, would be to check that the numerical solution is exactly what it should be. This will in general require exact knowledge of the numerical error, which we do not normally have (although we in the section Analysis of the difference equations establish such knowledge in simple cases). However, it is possible to look for solutions where we can show that the numerical error vanishes, i.e., the solution of the original continuous PDE problem is also a solution of the discrete equations. This property often arises if the exact solution of the PDE is a lower-order polynomial. (Truncation error analysis leads to error measures that involve derivatives of the exact solution. In the present problem, the truncation error involves 4th-order derivatives of $ u $ in space and time. Choosing $ u $ as a polynomial of degree three or less will therefore lead to vanishing error.)

We shall now illustrate the construction of an exact solution to both the PDE itself and the discrete equations. Our chosen manufactured solution is quadratic in space and linear in time. More specifically, we set $$ \begin{equation} \uex (x,t) = x(L-x)(1+{\half}t), \tag{30} \end{equation} $$ which by insertion in the PDE leads to $ f(x,t)=2(1+t)c^2 $. This $ \uex $ fulfills the boundary conditions $ u=0 $ and demands $ I(x)=x(L-x) $ and $ V(x)={\half}x(L-x) $.

To realize that the chosen $ \uex $ is also an exact solution of the discrete equations, we first remind ourselves that $ t_n=n\Delta t $ before we establish that $$ \begin{align} \lbrack D_tD_t t^2\rbrack^n &= \frac{t_{n+1}^2 - 2t_n^2 + t_{n-1}^2}{\Delta t^2} = (n+1)^2 -2n^2 + (n-1)^2 = 2, \tag{31}\\ \lbrack D_tD_t t\rbrack^n &= \frac{t_{n+1} - 2t_n + t_{n-1}}{\Delta t^2} = \frac{((n+1) -2n + (n-1))\Delta t}{\Delta t^2} = 0 \tp \tag{32} \end{align} $$ Hence, $$ [D_tD_t \uex]^n_i = x_i(L-x_i)[D_tD_t (1+{\half}t)]^n = x_i(L-x_i){\half}[D_tD_t t]^n = 0\tp$$ Similarly, we get that $$ \begin{align*} \lbrack D_xD_x \uex\rbrack^n_i &= (1+{\half}t_n)\lbrack D_xD_x (xL-x^2)\rbrack_i = (1+{\half}t_n)\lbrack LD_xD_x x - D_xD_x x^2\rbrack_i \\ &= -2(1+{\half}t_n) \tp \end{align*} $$ Now, $ f^n_i = 2(1+{\half}t_n)c^2 $, which results in $$ [D_tD_t \uex - c^2D_xD_x\uex - f]^n_i = 0 - c^2(-1)2(1 + {\half}t_n + 2(1+{\half}t_n)c^2 = 0\tp$$

Moreover, $ \uex(x_i,0)=I(x_i) $, $ \partial \uex/\partial t = V(x_i) $ at $ t=0 $, and $ \uex(x_0,t)=\uex(x_{N_x},0)=0 $. Also the modified scheme for the first time step is fulfilled by $ \uex(x_i,t_n) $.

Therefore, the exact solution $ \uex(x,t)=x(L-x)(1+t/2) $ of the PDE problem is also an exact solution of the discrete problem. We can use this result to check that the computed $ u^n_i $ values from an implementation equals $ \uex(x_i,t_n) $ within machine precision, regardless of the mesh spacings $ \Delta x $ and $ \Delta t $! Nevertheless, there might be stability restrictions on $ \Delta x $ and $ \Delta t $, so the test can only be run for a mesh that is compatible with the stability criterion (which in the present case is $ C\leq 1 $, to be derived later).

Notice. A product of quadratic or linear expressions in the various independent variables, as shown above, will often fulfill both the PDE problem and the discrete equations, and can therefore be very useful solutions for verifying implementations.

However, for 1D wave equations of the type $ u_{tt}=c^2u_{xx} $ we shall see that there is always another much more powerful way of generating exact solutions (which consists in just setting $ C=1 $ (!), as shown in the section Analysis of the difference equations).