Study guide: Solving nonlinear ODE and PDE problems
2016
What makes differential equations nonlinear?
- In linear differential equations, the unknown \( u \) or its derivatives appear in linear terms \( au(t) \), \( au'(t) \), \( a\nabla^2u \), where \( a \) is independent of \( u \).
- All other types of terms containing \( u \) are nonlinear and contain products of \( u \) or its derivatives.
Examples on linear and nonlinear differential equations
Linear ODE:
$$ u^{\prime} (t) = a(t)u(t) + b(t)$$
Nonlinear ODE:
$$ u^{\prime}(t) = u(t)(1 - u(t)) = u(t) - {\color{red}u(t)^2}$$
This (pendulum) ODE is also nonlinear:
$$ u^{\prime\prime} + \gamma\sin u = 0$$
because
$$ \sin u = u - \frac{1}{6}u^3 + \Oof{u^5},$$
contains products of \( u \)
Introduction of basic concepts
- Logistic ODE as simple model for a nonlinear problem
- Introduction of basic techniques:
- Explicit time integration (no nonlinearities)
- Implicit time integration (nonlinearities)
- Linearization and Picard iteration
- Linearization via Newton's method
- Linearization via a trick like geometric mean
- Numerical illustration of the performance
The scaled logistic ODE
$$ u^{\prime}(t) = u(t)(1 - u(t)) = u - {\color{red}u^2}$$
Linearization by explicit time discretization
Forward Euler method:
$$ \frac{u^{n+1} - u^n}{\Delta t} = u^n(1 - u^n)$$
gives a linear algebraic equation for the unknown value \( u^{n+1} \)!
Explicit time integration methods will (normally) linearize a nonlinear problem.
Another example: 2nd-order Runge-Kutta method
$$
\begin{align*}
u^* &= u^n + \Delta t u^n(1 - u^n),\\
u^{n+1} &= u^n + \Delta t \half \left(
u^n(1 - u^n) + u^*(1 - u^*))
\right)\tp
\end{align*}
$$
An implicit method: Backward Euler discretization
A backward time difference
$$ \frac{u^{n} - u^{n-1}}{\Delta t} = u^n(1 - u^n) $$
gives a nonlinear algebraic equation for the unknown \( u^n \). The equation is of quadratic type (which can easily be solved exactly):
$$ \Delta t (u^n)^2 + (1-\Delta t)u^n - u^{n-1} = 0 $$
Detour: new notation
To make formulas less overloaded and the mathematics as close as possible to computer code, a new notation is introduced:
- \( u^{(1)} \) means \( u^{n-1} \)
- In general: \( u^{(\ell)} \) means \( u^{n-\ell} \)
- \( u \) is the unknown (\( u^n \))
Nonlinear equation to solve in new notation:
$$
F(u) = \Delta t u^2 + (1-\Delta t)u - u^{(1)} = 0
$$
Exact solution of quadratic nonlinear equations
Solution of \( F(u)=0 \):
$$
u = \frac{1}{2\Delta t}
\left(-1+\Delta t \pm \sqrt{(1-\Delta t)^2 + 4\Delta t u^{(1)}}\right)
$$
Nonlinear algebraic equations may have multiple solutions!
How do we pick the right solution in this case?
Let's investigate the nature of the two roots:
>>> import sympy as sym
>>> dt, u_1, u = sym.symbols('dt u_1 u')
>>> r1, r2 = sym.solve(dt*u**2 + (1-dt)*u - u_1, u) # find roots
>>> r1
(dt - sqrt(dt**2 + 4*dt*u_1 - 2*dt + 1) - 1)/(2*dt)
>>> r2
(dt + sqrt(dt**2 + 4*dt*u_1 - 2*dt + 1) - 1)/(2*dt)
>>> print r1.series(dt, 0, 2)
-1/dt + 1 - u_1 + dt*(u_1**2 - u_1) + O(dt**2)
>>> print r2.series(dt, 0, 2)
u_1 + dt*(-u_1**2 + u_1) + O(dt**2)
The r1 root behaves as \( 1/\Delta t\rightarrow\infty \)
as \( \Delta t\rightarrow 0 \)! Therefore, only the r2 root is of
relevance.
Linearization
- In general, we cannot solve nonlinear algebraic equations with formulas
- We must linearize the equation, or create a recursive set of linearized equations whose solutions hopefully converge to the solution of the nonlinear equation
- Manual linearization may be an art
- Automatic linearization is possible (cf. Newton's method)
Examples will illustrate the points!
Picard iteration
Nonliner equation from Backward Euler scheme for logistic ODE:
$$ F(u) = au^2 + bu + c = 0$$
Let \( u^{-} \) be an available approximation of the unknown \( u \).
Linearization of \( u^2 \): \( u^{-}u \)
$$ F(u)\approx\hat F(u) = au^{-}u + bu + c = 0$$
But
- Problem: the solution \( u \) of \( \hat F(u)=0 \) is not the exact solution of \( F(u)=0 \)
- Solution: set \( u^{-}=u \) and repeat the procedure
The algorithm of Picard iteration
At a time level, set \( u^{-}=u^{(1)} \) (solution at previous time level) and iterate:
$$ u = -\frac{c}{au^{-} + b},\quad u^{-}\ \leftarrow\ u$$
This technique is known as
- fixed-point iteration
- successive substitutions
- nonlinear Richardson iteration
- Picard iteration
The algorithm of Picard iteration with classical math notation
- \( u^k \): computed approximation in iteration \( k \)
- \( u^{k+1} \) is the next approximation (unknown)
$$ au^k u^{k+1} + bu^{k+1} + c = 0\quad\Rightarrow\quad u^{k+1}
= -\frac{c}{au^k + b},\quad k=0,1,\ldots$$
Or with a time level \( n \) too:
$$ au^{n,k} u^{n,k+1} + bu^{n,k+1} - u^{n-1} = 0\quad\Rightarrow\quad u^{n,k+1}
= \frac{u^{n-1}}{au^{n,k} + b},\quad k=0,1,\ldots$$
Stopping criteria
Using change in solution:
$$ |u - u^{-}| \leq\epsilon_u$$
or change in residual:
$$ |F(u)|= |au^2+bu + c| < \epsilon_r$$
A single Picard iteration
Common simple and cheap technique: perform 1 single Picard iteration
$$
\frac{u^{n} - u^{n-1}}{\Delta t} = u^n(1 - {\color{red}u^{n-1}})
$$
Inconsistent time discretization (\( u(1-u) \) must be evaluated for \( n \), \( n-1 \), or \( n-\frac{1}{2} \)) - can produce quite inaccurate results, but is very popular.
Implicit Crank-Nicolson discretization
Crank-Nicolson discretization:
$$ [D_t u = u(1-u)]^{n+\half}$$
$$
\frac{u^{n+1}-u^n}{\Delta t} = u^{n+\half} -
(u^{n+\half})^2
$$
Approximate \( u^{n+\half} \) as usual by an arithmetic mean,
$$ u^{n+\half}\approx \half(u^n + u^{n+1})$$
$$ (u^{n+\half})^2\approx \frac{1}{4}(u^n + u^{n+1})^2\quad\hbox{(nonlinear term)}$$
which is nonlinear in the unknown \( u^{n+1} \).
Linearization by a geometric mean
Using a geometric mean for \( (u^{n+\half})^2 \) linearizes the nonlinear term \( (u^{n+\half})^2 \) (error \( \Oof{\Delta t^2} \) as in the discretization of \( u^{\prime} \)):
$$ (u^{n+\half})^2\approx u^nu^{n+1}$$
Arithmetic mean on the linear \( u^{n+\frac{1}{2}} \) term and a geometric mean for \( (u^{n+\half})^2 \) gives a linear equation for \( u^{n+1} \):
$$ \frac{{\color{red}u^{n+1}}-u^n}{\Delta t} =
\half(u^n + {\color{red}u^{n+1}}) - u^n{\color{red}u^{n+1}}$$
Note: Here we turned a nonlinear algebraic equation into a linear one. No need for iteration! (Consistent \( \Oof{\Delta t^2} \) approx.)
Newton's method
Write the nonlinear algebraic equation as
$$ F(u) = 0 $$
Newton's method: linearize \( F(u) \) by two terms from the Taylor series,
$$
\begin{align*}
F(u) &= F(u^{-}) + F^{\prime}(u^{-})(u - u^{-}) + {\half}F^{\prime\prime}(u^{-})(u-u^{-})^2
+\cdots\\
& \approx F(u^{-}) + F^{\prime}(u^{-})(u - u^{-}) \equiv \hat F(u)
\end{align*}
$$
The linear equation \( \hat F(u)=0 \) has the solution
$$ u = u^{-} - \frac{F(u^{-})}{F^{\prime}(u^{-})}$$
Note that \( \hat F \) in Picard and Newton are different!
Newton's method with an iteration index
$$ u^{k+1} = u^k - \frac{F(u^k)}{F^{\prime}(u^k)},\quad k=0,1,\ldots$$
Newton's method exhibits quadratic convergence if \( u^k \) is sufficiently close to the solution. Otherwise, the method may diverge.
Using Newton's method on the logistic ODE
$$ F(u) = au^2 + bu + c$$
$$ F^{\prime}(u) = 2au + b$$
The iteration method becomes
$$
u = u^{-} - \frac{a(u^{-})^2 + bu^{-} + c}{2au^{-} + b},\quad
u^{-}\ \leftarrow u
$$
Start of iteration: \( u^{-}=u^{(1)} \)
Using Newton's method on the logistic ODE with typical math notation
Set iteration start as \( u^{n,0}= u^{n-1} \) and iterate with explicit indices for time (\( n \)) and Newton iteration (\( k \)):
$$
u^{n,k+1} = u^{n,k} -
\frac{\Delta t (u^{n,k})^2 + (1-\Delta t)u^{n,k} - u^{n-1}}
{2\Delta t u^{n,k} + 1 - \Delta t}
$$
Compare notation with
$$
u = u^{-} -
\frac{\Delta t (u^{-})^2 + (1-\Delta t)u^{-} - u^{(1)}}
{2\Delta t u^{-} + 1 - \Delta t}
$$
Relaxation may improve the convergence
- Problem: Picard and Newton iteration may change the solution too much
- Remedy: relaxation (less change in the solution)
- Let \( u^* \) be the suggested new value from Picard or Newton iteration
Relaxation with relaxation parameter \( \omega \) (weight old and new value):
$$ u = \omega u^* + (1-\omega) u^{-},\quad \omega \leq 1$$
Simple formula when used in Newton's method:
$$
u = u^{-} - \omega \frac{F(u^{-})}{F^{\prime}(u^{-})}
$$
Implementation; part 1
Program logistic.py
def BE_logistic(u0, dt, Nt, choice='Picard',
eps_r=1E-3, omega=1, max_iter=1000):
if choice == 'Picard1':
choice = 'Picard'; max_iter = 1
u = np.zeros(Nt+1)
iterations = []
u[0] = u0
for n in range(1, Nt+1):
a = dt
b = 1 - dt
c = -u[n-1]
if choice == 'Picard':
def F(u):
return a*u**2 + b*u + c
u_ = u[n-1]
k = 0
while abs(F(u_)) > eps_r and k < max_iter:
u_ = omega*(-c/(a*u_ + b)) + (1-omega)*u_
k += 1
u[n] = u_
iterations.append(k)
Implementation; part 2
def BE_logistic(u0, dt, Nt, choice='Picard',
eps_r=1E-3, omega=1, max_iter=1000):
...
elif choice == 'Newton':
def F(u):
return a*u**2 + b*u + c
def dF(u):
return 2*a*u + b
u_ = u[n-1]
k = 0
while abs(F(u_)) > eps_r and k < max_iter:
u_ = u_ - omega*F(u_)/dF(u_)
k += 1
u[n] = u_
iterations.append(k)
return u, iterations
Implementation; part 3
The Crank-Nicolson method with a geometric mean:
def CN_logistic(u0, dt, Nt):
u = np.zeros(Nt+1)
u[0] = u0
for n in range(0, Nt):
u[n+1] = (1 + 0.5*dt)/(1 + dt*u[n] - 0.5*dt)*u[n]
return u
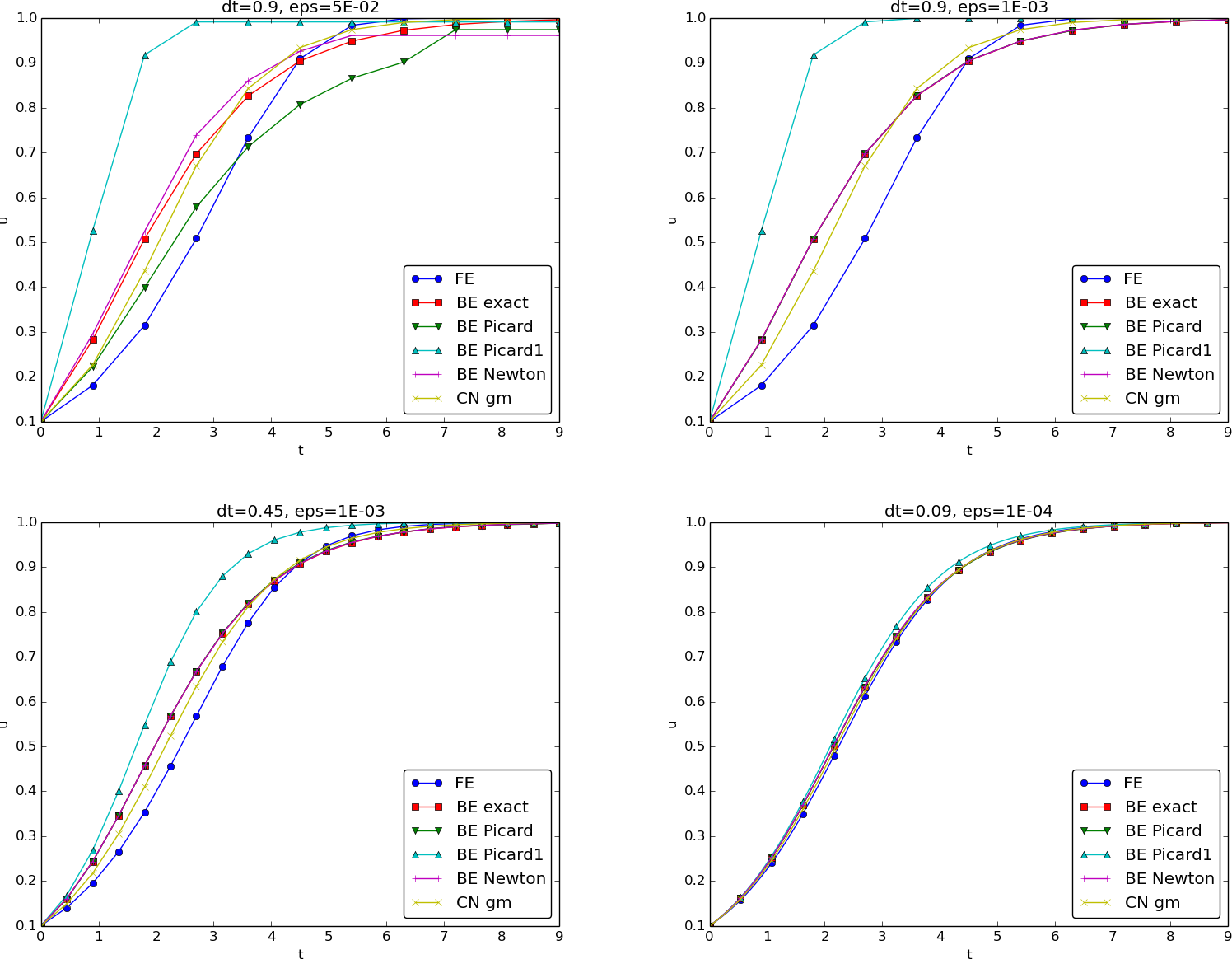
Experiments: accuracy of iteration methods
Figure 1: The impact of solution strategies and for four different time step lengths on the solution.
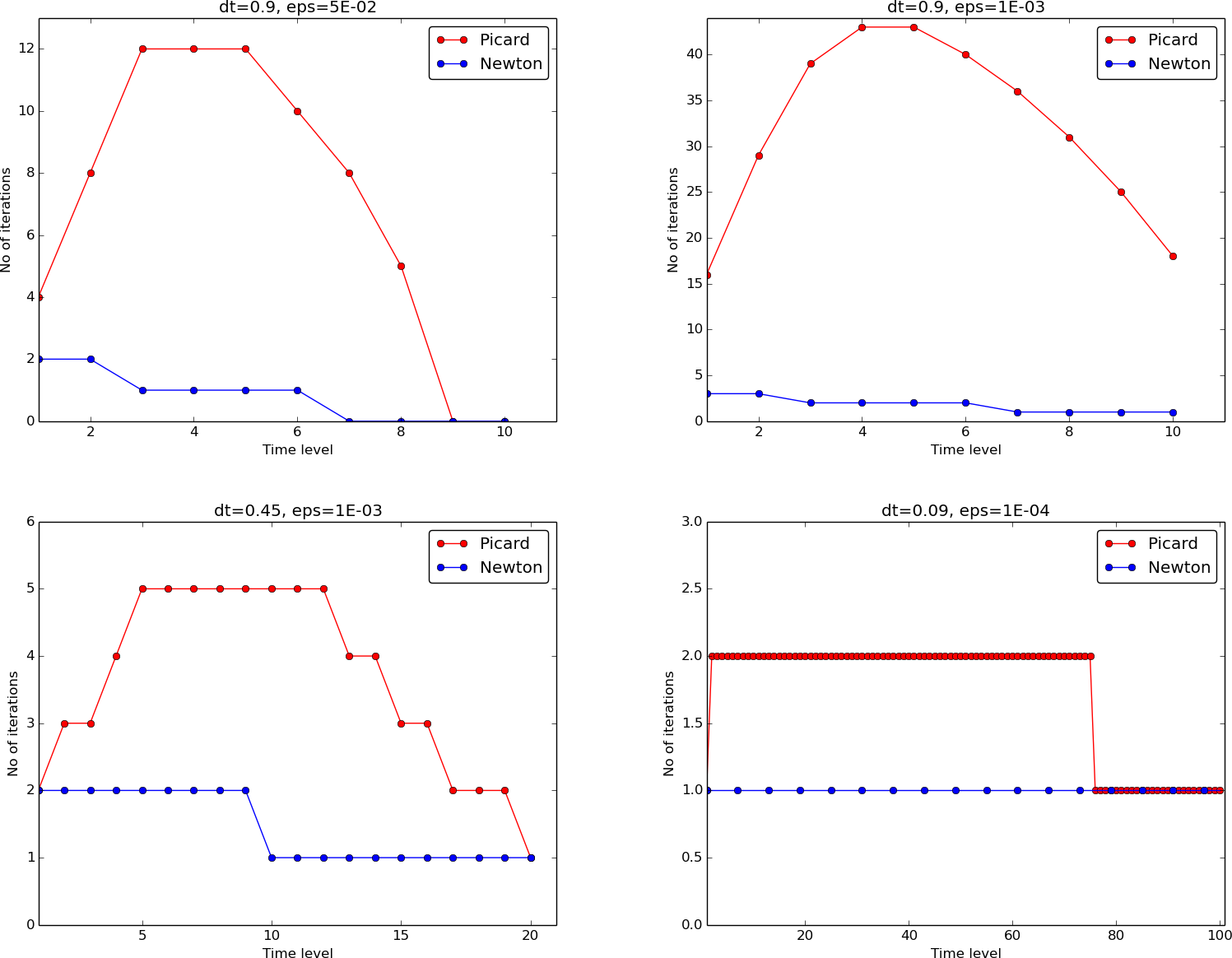
Experiments: number of iterations
Figure 2: Comparison of the number of iterations at various time levels for Picard and Newton iteration.
The effect of relaxation can potentially be great!
- \( \Delta t=0.9 \): Picard required 32 iterations on average
- \( \omega =0.8 \): 7 iterations
- \( \omega =0.5 \): 2 iterations (!) - optimal choice
Other \( \omega=1 \) experiments:
| \( \Delta t \) | \( \epsilon_r \) | Picard | Newton |
|---|---|---|---|
| \( 0.2 \) | \( 10^{-7} \) | 5 | 2 |
| \( 0.2 \) | \( 10^{-3} \) | 2 | 1 |
| \( 0.4 \) | \( 10^{-7} \) | 12 | 3 |
| \( 0.4 \) | \( 10^{-3} \) | 4 | 2 |
| \( 0.8 \) | \( 10^{-7} \) | 58 | 3 |
| \( 0.8 \) | \( 10^{-3} \) | 4 | 2 |
Generalization to a general nonlinear ODE
$$
u^{\prime} = f(u, t)
$$
Note: \( f \) is in general nonlinear in \( u \) so the ODE is nonlinear
Explicit time discretization
Forward Euler and all explicit methods sample \( f \) with known values and all nonlinearities are gone:
$$ \frac{{\color{red}u^{n+1}}-u^n}{\Delta t} = f(u^n, t_n) $$
Backward Euler discretization
Backward Euler \( [D_t^- u = f]^n \) leads to nonlinear algebraic equations:
$$ F(u^n) = u^{n} - \Delta t\, f(u^n, t_n) - u^{n-1}=0$$
Alternative notation:
$$ F(u) = u - \Delta t\, f(u, t_n) - u^{(1)} = 0$$
Picard iteration for Backward Euler scheme
A simple Picard iteration, not knowing anything about the nonlinear structure of \( f \), must approximate \( f(u,t_n) \) by \( f(u^{-},t_n) \):
$$ \hat F(u) = u - \Delta t\, f(u^{-},t_n) - u^{(1)}$$
The iteration starts with \( u^{-}=u^{(1)} \) and proceeds with repeating
$$ u^* = \Delta t\, f(u^{-},t_n) + u^{(1)},\quad
u = \omega u^* + (1-\omega)u^{-},
\quad u^{-}\ \leftarrow\ u$$
until a stopping criterion is fulfilled.
Manual linearization for a given \( f(u,t) \)
- \( f(u^{-},t) \): explicit treatment of \( f \)
(as in time-discretization) - \( f(u,t) \): fully implicit treatment of \( f \)
- If \( f \) has some structure, say \( f(u,t)=u^3 \), we may think of a partially implicit treatment: \( (u^{-})^2u \)
- More implicit treatment of \( f \) often gives faster
convergence
(as it gives more stable time discretizations)
Trick for partially implicit treatment of a general \( f(u,t) \):
$$ f(u^{-},t)\frac{u}{u^{-}} $$
(Idea: \( u\approx u^{-} \))
Computational experiments with partially implicit treatment of \( f \)
- \( f(u,t)=-u^3 \):
- \( (u^{-})^3 \) linearization: 22, 9, 6 iterations
- \( (u^{-})^2u \) linearization: 8, 5, 4 iterations
- \( f(u,t)=e^{-u} \): a trick \( f(u^{-},t)u/u^{-} \) has no effect
- \( f(u,t)=\sin(2(u+1)) \): a trick \( f(u^{-},t)u/u^{-} \) has effect
(7, 9, 11 iterations vs 17, 21, 20)
Newton's method for Backward Euler scheme
Newton's method requires the computation of the derivative
$$ F^{\prime}(u) = 1 - \Delta t\frac{\partial f}{\partial u}(u,t_n)$$
Start with \( u^{-}=u^{(1)} \), then iterate
$$
u = u^{-} - \omega \frac{F(u^{-})}{F^{\prime}(u^{-})}
= u^{-} - \omega \frac{u^{-} - \Delta t\, f(u^{-},t_{n}) -u^{(1)}}{1 - \Delta t
\frac{\partial}{\partial u}f(u^{-},t_n)}
$$
Crank-Nicolson discretization
The standard Crank-Nicolson scheme with arithmetic mean approximation of \( f \) reads
$$ \frac{u^{n+1} - u^n}{\Delta t} = \half(f(u^{n+1}, t_{n+1})
+ f(u^n, t_n))$$
Nonlinear algebraic equation:
$$
F(u) = u - u^{(1)} - \Delta t{\half}f(u,t_{n+1}) -
\Delta t{\half}f(u^{(1)},t_{n}) = 0
$$
Picard and Newton iteration in the Crank-Nicolson case
Picard iteration (for a general \( f \)):
$$ \hat F(u) = u - u^{(1)} - \Delta t{\half}f(u^{-},t_{n+1}) -
\Delta t{\half}f(u^{(1)},t_{n})$$
Newton's method:
$$
F(u) = u - u^{(1)} - \Delta t{\half}f(u,t_{n+1}) -
\Delta t{\half}f(u^{(1)},t_{n})
$$
$$ F^{\prime}(u)= 1 - \half\Delta t\frac{\partial f}{\partial u}(u,t_{n+1})$$
Systems of ODEs
$$
\begin{align*}
\frac{d}{dt}u_0(t) &= f_0(u_0(t),u_1(t),\ldots,u_N(t),t)\\
\frac{d}{dt}u_1(t) &= f_1(u_0(t),u_1(t),\ldots,u_N(t),t),\\
&\vdots\\
\frac{d}{dt}u_N(t) &= f_N(u_0(t),u_1(t),\ldots,u_N(t),t)
\end{align*}
$$
Introduce vector notation:
- \( u=(u_0(t),u_1(t),\ldots,u_N(t)) \)
- \( f=(f_0(u,t),f_1(u,t),\ldots,f_N(u,t)) \)
Vector form:
$$ u^{\prime} = f(u,t),\quad u(0)=U_0 $$
Strategy: apply scalar scheme to each component
A Backward Euler scheme for the vector ODE \( u^{\prime}=f(u,t) \)
$$
\begin{align*}
\frac{u_0^n- u_0^{n-1}}{\Delta t} &= f_0(u^n,t_n)\\
\frac{u_1^n- u_1^{n-1}}{\Delta t} &= f_1(u^n,t_n)\\
&\vdots\\
\frac{u_N^n- u_N^{n-1}}{\Delta t} &= f_N(u^n,t_n)
\end{align*}
$$
This can be written more compactly in vector form as
$$ \frac{u^n- u^{n-1}}{\Delta t} = f(u^n,t_n)$$
This is a system of nonlinear algebraic equations,
$$ u^n - \Delta t\,f(u^n,t_n) - u^{n-1}=0,$$
or written out
$$
\begin{align*}
u_0^n - \Delta t\, f_0(u^n,t_n) - u_0^{n-1} &= 0,\\
&\vdots\\
u_N^n - \Delta t\, f_N(u^n,t_n) - u_N^{n-1} &= 0\tp
\end{align*}
$$
Example: Crank-Nicolson scheme for the oscillating pendulum model
The scaled equations for an oscillating pendulum:
$$
\begin{align}
\dot\omega &= -\sin\theta -\beta \omega |\omega|,
\tag{1}\\
\dot\theta &= \omega,
\tag{2}
\end{align}
$$
Set \( u_0=\omega \), \( u_1=\theta \)
$$
\begin{align*}
u_0^{\prime} = f_0(u,t) &= -\sin u_1 - \beta u_0|u_0|,\\
u_1^{\prime} = f_1(u,t) &= u_0\tp
\end{align*}
$$
Crank-Nicolson discretization:
$$
\begin{align}
\frac{u_0^{n+1}-u_0^{n}}{\Delta t} &= -\sin u_1^{n+\frac{1}{2}}
- \beta u_0^{n+\frac{1}{2}}|u_0^{n+\frac{1}{2}}|
\approx -\sin\left(\frac{1}{2}(u_1^{n+1} + u_1^n)\right)
- \beta\frac{1}{4} (u_0^{n+1} + u_0^n)|u_0^{n+1}+u_0^n|,
\tag{3}\\
\frac{u_1^{n+1}-u_1^n}{\Delta t} &= u_0^{n+\frac{1}{2}}\approx
\frac{1}{2} (u_0^{n+1}+u_0^n)\tp
\tag{4}
\end{align}
$$
The nonlinear \( 2\times 2 \) system
Introduce \( u_0 \) and \( u_1 \) for \( u_0^{n+1} \) and \( u_1^{n+1} \), write \( u_0^{(1)} \) and \( u_1^{(1)} \) for \( u_0^n \) and \( u_1^n \), and rearrange:
$$
\begin{align*}
F_0(u_0,u_1) &=
{\color{red}u_0}
- u_0^{(1)} + \Delta t\,\sin\left(\frac{1}{2}({\color{red}u_1}
+ u_1^{(1)})\right)
+ \frac{1}{4}\Delta t\beta ({\color{red}u_0} + u_0^{(1)})
|{\color{red}u_0} + u_0^{(1)}| =0
\\
F_1(u_0,u_1) &=
{\color{red}u_1} - u_1^{(1)} -\frac{1}{2}\Delta t({\color{red}u_0}
+ u_0^{(1)}) =0
\end{align*}
$$
Systems of nonlinear algebraic equations
$$
\begin{align*}
x\cos y + y^3 & = 0\\
y^2e^x + xy &= 2
\end{align*}
$$
Systems of nonlinear algebraic equations arise from solving systems of ODEs or solving PDEs
Notation for general systems of algebraic equations
$$ F(u) = 0$$
where
$$ u=(u_0,\ldots,u_N),\quad F=(F_0,\ldots,F_N)$$
Special linear system-type structure
(arises frequently in PDE problems):
$$ A(u)u = b(u)$$
Picard iteration
Picard iteration for \( F(u)=0 \) is meaningless unless there is some structure that we can linearize. For \( A(u)u=b(u) \) we can linearize
$$ A(u^{-})u = b(u^{-})$$
Note: we solve a system of nonlinear algebraic equations as a sequence of linear systems.
Algorithm for relaxed Picard iteration
Given \( A(u)u=b(u) \) and an initial guess \( u^{-} \), iterate until convergence:
- solve \( A(u^{-})u^* = b(u^{-}) \) with respect to \( u^* \)
- \( u = \omega u^* + (1-\omega) u^{-} \)
- \( u^{-}\ \leftarrow\ u \)
"Until convergence": \( ||u - u^{-}|| \leq \epsilon_u \) or \( ||A(u)u-b|| \leq\epsilon_r \)
Newton's method for \( F(u)=0 \)
Linearization of \( F(u)=0 \) equation via multi-dimensional Taylor series:
$$ F(u) = F(u^{-}) + J(u^{-}) \cdot (u - u^{-}) + \mathcal{O}(||u - u^{-}||^2) $$
where \( J \) is the Jacobian of \( F \), sometimes denoted \( \nabla_uF \), defined by
$$ J_{i,j} = \frac{\partial F_i}{\partial u_j}$$
Approximate the original nonlinear system \( F(u)=0 \) by
$$ \hat F(u) = F(u^{-}) + J(u^{-}) \cdot \delta u =0,\quad
\delta u = u - u^{-}$$
which is linear vector equation in \( u \)
Algorithm for Newton's method
$$ \underline{F(u^{-})}_{\mbox{vector}} +
\underline{J(u^{-})}_{\mbox{matrix}} \cdot
\underline{\delta u}_{\mbox{vector}} =0$$
Solution by a two-step procedure:
- solve linear system \( J(u^{-})\delta u = -F(u^{-}) \) wrt \( \delta u \)
- update \( u = u^{-} + \delta u \)
Relaxed update:
$$ u = \omega(u^{-} +\delta u)
+ (1-\omega)u^{-} = u^{-} + \omega\delta u
$$
Newton's method for \( A(u)u=b(u) \)
For
$$ F_i = \sum_k A_{i,k}(u)u_k - b_i(u)$$
one gets
$$
J_{i,j} = \frac{\partial F_i}{\partial u_j}
= A_{i,j}+\sum_k \frac{\partial A_{i,k}}{\partial u_j}u_k
-
\frac{\partial b_i}{\partial u_j}
$$
Matrix form:
$$ (A + A^{\prime}u - b^{\prime})\delta u = -Au + b$$
$$ (A(u^{-}) + A^{\prime}(u^{-})u^{-} - b^{\prime}(u^{-}))\delta u
= -A(u^{-})u^{-} + b(u^{-})$$
Comparison of Newton and Picard iteration
Newton:
$$ (A(u^{-}) + A^{\prime}(u^{-})u^{-} - b^{\prime}(u^{-}))\delta u
= -A(u^{-})u^{-} + b(u^{-})$$
Rewrite:
$$ \underbrace{A(u^{-})(u^{-}+\delta u) - b(u^{-})}_{\hbox{Picard system}}
+\, \gamma (A^{\prime}(u^{-})u^{-} - b^{\prime}(u^{-}))\delta u
= 0$$
All the "Picard terms" are contained in the Newton formulation.
Combined Picard-Newton algorithm
Write a common Picard-Newton algorithm so we can trivially switch between the two methods (e.g., start with Picard, get faster convergence with Newton when \( u \) is closer to the solution)
Given \( A(u) \), \( b(u) \), and an initial guess \( u^{-} \), iterate until convergence:
- solve \( (A + \gamma(A^{\prime}(u^{-})u^{-} - b^{\prime}(u^{-})))\delta u = -A(u^{-})u^{-} + b(u^{-}) \) with respect to \( \delta u \)
- \( u = u^{-} + \omega\delta u \)
- \( u^{-}\ \leftarrow\ u \)
Note:
- \( \gamma =1 \): Newton's method
- \( \gamma =0 \): Picard iteration
Stopping criteria
Let \( ||\cdot|| \) be the standard Eucledian vector norm. Several termination criteria are much in use:
- Absolute change in solution: \( ||u - u^{-}||\leq \epsilon_u \)
- Relative change in solution: \( ||u - u^{-}||\leq \epsilon_u ||u_0|| \), where \( u_0 \) denotes the start value of \( u^{-} \) in the iteration
- Absolute residual: \( ||F(u)|| \leq \epsilon_r \)
- Relative residual: \( ||F(u)|| \leq \epsilon_r ||F(u_0)|| \)
- Max no of iterations: stop when \( k > k_{\max} \)
Combination of absolute and relative stopping criteria
Problem with relative criterion: a small \( ||F(u_0)|| \) (because \( u_0\approx u \), perhaps because of small \( \Delta t \)) must be significantly reduced. Better with absolute criterion.
- Can make combined absolute-relative criterion
- \( \epsilon_{rr} \): tolerance for relative part
- \( \epsilon_{ra} \): tolerance for absolute part
$$
||F(u)|| \leq \epsilon_{rr} ||F(u_0)|| + \epsilon_{ra}
$$
$$
||F(u)|| \leq \epsilon_{rr} ||F(u_0)|| + \epsilon_{ra}
\quad\hbox{or}\quad
||\delta u|| \leq \epsilon_{ur} ||u_0|| + \epsilon_{ua}
\quad\hbox{or}\quad
k>k_{\max}
$$
Example: A nonlinear ODE model from epidemiology
Spreading of a disease (e.g., a flu) can be modeled by a \( 2\times 2 \) ODE system
$$
\begin{align*}
S^{\prime} &= -\beta SI\\
I^{\prime} &= \beta SI - \nu I
\end{align*}
$$
Here:
- \( S(t) \) is the number of people who can get ill (susceptibles)
- \( I(t) \) is the number of people who are ill (infected)
- Must know \( \beta >0 \) (danger of getting ill) and
\( \nu >0 \) (\( 1/\nu \): expected recovery time)
Implicit time discretization
A Crank-Nicolson scheme:
$$
\begin{align*}
\frac{S^{n+1}-S^n}{\Delta t} &= -\beta [SI]^{n+\half}
\approx -\frac{\beta}{2}(S^nI^n + S^{n+1}I^{n+1})\\
\frac{I^{n+1}-I^n}{\Delta t} &= \beta [SI]^{n+\half} -
\nu I^{n+\half}
\approx \frac{\beta}{2}(S^nI^n + S^{n+1}I^{n+1}) -
\frac{\nu}{2}(I^n + I^{n+1})
\end{align*}
$$
New notation: \( S \) for \( S^{n+1} \), \( S^{(1)} \) for \( S^n \), \( I \) for \( I^{n+1} \), \( I^{(1)} \) for \( I^n \)
$$
\begin{align*}
F_S(S,I) &= S - S^{(1)} +
\half\Delta t\beta(S^{(1)}I^{(1)} + SI) = 0\\
F_I(S,I) &= I - I^{(1)} -
\half\Delta t\beta(S^{(1)}I^{(1)} + SI) +
\half\Delta t\nu(I^{(1)} + I) =0
\end{align*}
$$
A Picard iteration
- We have approximations \( S^{-} \) and \( I^{-} \) to \( S \) and \( I \).
- Linearize \( SI \) in \( S \) ODE as \( I^{-}S \) (linear equation in \( S \)!)
- Linearize \( SI \) in \( I \) ODE as \( S^{-}I \) (linear equation in \( I \)!)
$$
\begin{align*}
S &= \frac{S^{(1)} - \half\Delta t\beta S^{(1)}I^{(1)}}
{1 + \half\Delta t\beta I^{-}}
\\
I &= \frac{I^{(1)} + \half\Delta t\beta S^{(1)}I^{(1)} - \half\Delta t\nu I^{(1)}}
{1 - \half\Delta t\beta S^{-} + \half\Delta t \nu}
\end{align*}
$$
Before a new iteration: \( S^{-}\ \leftarrow\ S \) and
\( I^{-}\ \leftarrow\ I \)
Newton's method
$$ F(u)=0,\quad F=(F_S,F_I),\ u=(S,I) $$
Jacobian:
$$
J = \left(\begin{array}{cc}
\frac{\partial}{\partial S} F_S & \frac{\partial}{\partial I}F_S\\
\frac{\partial}{\partial S} F_I & \frac{\partial}{\partial I}F_I
\end{array}\right)
= \left(\begin{array}{cc}
1 + \half\Delta t\beta I & \half\Delta t\beta S\\
- \half\Delta t\beta I & 1 - \half\Delta t\beta S +
\half\Delta t\nu
\end{array}\right)
$$
Newton system: \( J(u^{-})\delta u = -F(u^{-}) \)
$$
\begin{align*}
&
\left(\begin{array}{cc}
1 + \half\Delta t\beta I^{-} & \half\Delta t\beta S^{-}\\
- \half\Delta t\beta I^{-} & 1 - \half\Delta t\beta S^{-} +
\half\Delta t\nu
\end{array}\right)
\left(\begin{array}{c}
\delta S\\
\delta I
\end{array}\right)
=\\
& \qquad\qquad
\left(\begin{array}{c}
S^{-} - S^{(1)} + \half\Delta t\beta(S^{(1)}I^{(1)} + S^{-}I^{-})\\
I^{-} - I^{(1)} - \half\Delta t\beta(S^{(1)}I^{(1)} + S^{-}I^{-}) -
\half\Delta t\nu(I^{(1)} + I^{-})
\end{array}\right)
\end{align*}
$$
Actually no need to bother with nonlinear algebraic equations for this particular model...
For this particular system of ODEs, explicit time integration methods work very well. Even a Forward Euler scheme is fine, but the 4-th order Runge-Kutta method is an excellent balance between high accuracy, high efficiency, and simplicity.
Linearization at the differential equation level
Goal: linearize a PDE like
$$
\frac{\partial u}{\partial t} = \nabla\cdot ({\color{red}\dfc(u)\nabla u})
+ {\color{red}f(u)}
$$
PDE problem
$$
\begin{align*}
\frac{\partial u}{\partial t} &= \nabla\cdot (\dfc(u)\nabla u) + f(u),\quad
&\x\in\Omega,\ t\in (0,T]
\\
-\dfc(u)\frac{\partial u}{\partial n} &= g,\quad &\x\in\partial\Omega_N,\
t\in (0,T]
\\
u &= u_0,\quad &\x\in\partial\Omega_D,\ t\in (0,T]
\end{align*}
$$
Explicit time integration
Forward Euler method:
$$ [D_t^+ u = \nabla\cdot (\dfc(u)\nabla u) + f(u)]^n$$
$$ \frac{u^{n+1} - u^n}{\Delta t} = \nabla\cdot (\dfc(u^n)\nabla u^n)
+ f(u^n)$$
This is a linear equation in the unknown \( u^{n+1}(\x) \), with solution
$$ u^{n+1} = u^n + \Delta t\nabla\cdot (\dfc(u^n)\nabla u^n) +
\Delta t f(u^n) $$
Disadvantage: \( \Delta t \leq (\max\alpha)^{-1}(\Delta x^2 + \Delta y^2 + \Delta z^2) \)
Backward Euler scheme
Backward Euler scheme:
$$ [D_t^- u = \nabla\cdot (\dfc(u)\nabla u) + f(u)]^n$$
Written out:
$$
\frac{u^{n} - u^{n-1}}{\Delta t} = \nabla\cdot (\dfc(u^n)\nabla u^n)
+ f(u^n)
$$
This is a nonlinear, stationary PDE for the unknown function \( u^n(\x) \)
Picard iteration for Backward Euler scheme
We have
$$
\frac{u^{n} - u^{n-1}}{\Delta t} = \nabla\cdot (\dfc(u^n)\nabla u^n)
+ f(u^n)
$$
Picard iteration:
$$
\frac{u^{n,k+1} - u^{n-1}}{\Delta t} = \nabla\cdot (\dfc(u^{n,k})
\nabla u^{n,k+1})
+ f(u^{n,k})
$$
Start iteration with \( u^{n,0}=u^{n-1} \)
Picard iteration with alternative notation
$$
\frac{u^{n,k+1} - u^{n-1}}{\Delta t} = \nabla\cdot (\dfc(u^{n,k})
\nabla u^{n,k+1})
+ f(u^{n,k})
$$
Rewrite with a simplified, implementation-friendly notation:
- \( u \) means the unknown \( u^{n,k+1} \) to solve for
- \( u^{-} \) means the most recent approximation: \( u^{n,k} \)
- \( u^{(1)} \) means \( u^{n-1} \) (\( u^{(\ell)} \) means \( u^{n-\ell} \))
$$
\frac{u - u^{(1)}}{\Delta t} = \nabla\cdot (\dfc(u^{-})
\nabla u)
+ f(u^{-})
$$
Start iteration with \( u^{-}=u^{(1)} \); update with \( u^{-} \) to \( u \).
Backward Euler scheme and Newton's method
Let \( u^{n,k} \) be the most recently computed approximation to the unknown \( u^n \). We seek a better approximation
$$
u^{n} = u^{n,k} + \delta u
$$
- Insert \( u^{n} = u^{n,k} + \delta u \) in the PDE
- Taylor expand the nonlinearities and keep only terms that are linear in \( \delta u \)
Result: a linear PDE for the approximate correction \( \delta u \)
Calculation details of Newton's method at the PDE level
Insert \( u^{n,k} +\delta u \) for \( u^n \) in PDE:
$$
\frac{u^{n,k} +\delta u - u^{n-1}}{\Delta t} =
\nabla\cdot (\dfc(u^{n,k} + \delta u)\nabla (u^{n,k}+\delta u))
+ f(u^{n,k}+\delta u)
$$
Taylor expand \( \dfc(u^{n,k} + \delta u) \) and \( f(u^{n,k}+\delta u) \):
$$
\begin{align*}
\dfc(u^{n,k} + \delta u) & = \dfc(u^{n,k}) + \frac{d\dfc}{du}(u^{n,k})
\delta u + \Oof{\delta u^2}\approx \dfc(u^{n,k}) + \dfc^{\prime}(u^{n,k})\delta u\\
f(u^{n,k}+\delta u) &= f(u^{n,k}) + \frac{df}{du}(u^{n,k})\delta u
+ \Oof{\delta u^2}\approx f(u^{n,k}) + f^{\prime}(u^{n,k})\delta u
\end{align*}
$$
Calculation details of Newton's method at the PDE level
Inserting linear approximations of \( \dfc \) and \( f \):
$$
\begin{align*}
\frac{u^{n,k} +\delta u - u^{n-1}}{\Delta t} &=
\nabla\cdot (\dfc(u^{n,k})\nabla u^{n,k}) + f(u^{n,k}) + \\
&\quad \nabla\cdot (\dfc(u^{n,k})\nabla \delta u)
+ \nabla\cdot (\dfc^{\prime}(u^{n,k})\delta u\nabla u^{n,k}) + \\
&\quad \nabla\cdot (\dfc^{\prime}(u^{n,k})\underbrace{\delta u\nabla \delta u}_{\mbox{dropped}})
+ f^{\prime}(u^{n,k})\delta u
\end{align*}
$$
Note: \( \dfc^{\prime}(u^{n,k})\delta u\nabla \delta u \) is \( \Oof{\delta u^2} \) and therefore omitted.
Result of Newton's method at the PDE level
$$ \delta F(\delta u; u^{n,k}) = -F(u^{n,k})$$
with
$$
\begin{align*}
F(u^{n,k}) &= \frac{u^{n,k} - u^{n-1}}{\Delta t} -
\nabla\cdot (\dfc(u^{n,k})\nabla u^{n,k}) - f(u^{n,k})
\\
\delta F(\delta u; u^{n,k}) &=
\frac{1}{\Delta t}\delta u -
\nabla\cdot (\dfc(u^{n,k})\nabla \delta u) - \\
&\qquad \nabla\cdot (\dfc^{\prime}(u^{n,k})\delta u\nabla u^{n,k})
- f^{\prime}(u^{n,k})\delta u
\end{align*}
$$
Note:
- \( \delta F \) is linear in \( \delta u \)
- \( F \) contains only known terms
Similarity with Picard iteration
Rewrite the PDE for \( \delta u \) using \( u^{n,k} + \delta u =u^{n,k+1} \):
$$
\begin{align*}
& \frac{u^{n,k+1} - u^{n-1}}{\Delta t} =
\nabla\cdot (\dfc(u^{n,k})\nabla u^{n,k+1}) + f(u^{n,k})\\
&\qquad + \nabla\cdot (\dfc^{\prime}(u^{n,k})\delta u\nabla u^{n,k})
+ f^{\prime}(u^{n,k})\delta u
\end{align*}
$$
Note:
- The first line is the same PDE as arise in the Picard iteration
- The remaining terms arise from the differentiations in Newton's method
Using new notation for implementation
- \( u \) for \( u^n \)
- \( u^{-} \) for \( u^{n,k} \)
- \( u^{(1)} \) for \( u^{n-1} \)
$$ \delta F(\delta u; u^{-}) =- F(u^{-})\quad\hbox{(PDE)}$$
$$
\begin{align*}
F(u^{-}) &= \frac{u^{-} - u^{(1)}}{\Delta t} -
\nabla\cdot (\dfc(u^{-})\nabla u^{-}) - f(u^{-})
\\
\delta F(\delta u; u^{-}) &=
\frac{1}{\Delta t}\delta u -
\nabla\cdot (\dfc(u^{-})\nabla \delta u) \ - \nonumber\\
&\quad \nabla\cdot (\dfc^{\prime}(u^{-})\delta u\nabla u^{-})
- f^{\prime}(u^{-})\delta u
\end{align*}
$$
Combined Picard and Newton formulation
$$
\begin{align*}
& \frac{u - u^{(1)}}{\Delta t} =
\nabla\cdot (\dfc(u^{-})\nabla u) + f(u^{-}) + \\
&\qquad \gamma(\nabla\cdot (\dfc^{\prime}(u^{-})(u - u^{-})\nabla u^{-})
+ f^{\prime}(u^{-})(u - u^{-}))
\end{align*}
$$
Observe:
- \( \gamma=0 \): Picard iteration
- \( \gamma=1 \): Newton's method
Why is this formulation convenient? Easy to switch (start with Picard, use Newton close to solution)
Crank-Nicolson discretization
Crank-Nicolson discretization applies a centered difference at \( t_{n+\frac{1}{2}} \):
$$ [D_t u = \nabla\cdot (\dfc(u)\nabla u) + f(u)]^{n+\frac{1}{2}}\tp$$
Many choices of formulating an arithmetic mean:
$$
\begin{align*}
[f(u)]^{n+\frac{1}{2}} &\approx f(\frac{1}{2}(u^n + u^{n+1}))
= [f(\overline{u}^t)]^{n+\frac{1}{2}}\\
[f(u)]^{n+\frac{1}{2}} &\approx \frac{1}{2}(f(u^n) + f(u^{n+1}))
=[\overline{f(u)}^t]^{n+\frac{1}{2}}\\
[\dfc(u)\nabla u]^{n+\frac{1}{2}} &\approx
\dfc(\frac{1}{2}(u^n + u^{n+1}))\nabla (\frac{1}{2}(u^n + u^{n+1}))
= \dfc(\overline{u}^t)\nabla \overline{u}^t]^{n+\frac{1}{2}}\\
[\dfc(u)\nabla u]^{n+\frac{1}{2}} &\approx
\frac{1}{2}(\dfc(u^n) + \dfc(u^{n+1}))\nabla (\frac{1}{2}(u^n + u^{n+1}))
= [\overline{\dfc(u)}^t\nabla\overline{u}^t]^{n+\frac{1}{2}}\\
[\dfc(u)\nabla u]^{n+\frac{1}{2}} &\approx
\frac{1}{2}(\dfc(u^n)\nabla u^n + \dfc(u^{n+1})\nabla u^{n+1})
= [\overline{\dfc(u)\nabla u}^t]^{n+\frac{1}{2}}
\end{align*}
$$
Arithmetic means: which variant is best?
Is there any differences in accuracy between
- the product of arithmetic means
- the arithmetic mean of a product
More precisely,
$$
\begin{align*}
[PQ]^{n+\frac{1}{2}} = P^{n+\frac{1}{2}}Q^{n+\frac{1}{2}}
&\approx
\frac{1}{2}(P^n + P^{n+1})\frac{1}{2}(Q^n + Q^{n+1})\\
[PQ]^{n+\frac{1}{2}} & \approx \frac{1}{2}(P^nQ^n + P^{n+1}Q^{n+1})
\end{align*}
$$
It can be shown (by Taylor series around \( t_{n+\frac{1}{2}} \)) that both approximations are \( \Oof{\Delta t^2} \)
Solution of nonlinear equations in the Crank-Nicolson scheme
No big difference from the Backward Euler case, just more terms:
- Identify the \( F(u)=0 \) for the unknown \( u^{n+1} \)
- Apply Picard iteration or Newton's method to the PDE
- Identify the sequence of linearized PDEs and iterate
Discretization of 1D stationary nonlinear differential equations
Differential equation:
$$
-(\dfc(u)u^{\prime})^{\prime} + au = f(u),\quad x\in (0,L)
$$
Boundary conditions:
$$
\dfc(u(0))u^{\prime}(0) = C,\quad u(L)=D
$$
Relevance of this stationary 1D problem
1. As stationary limit of a diffusion PDE
$$ u_t = (\alpha(u)u_x)_x + au + f(u) $$
(\( u_t\rightarrow 0 \))
2. The time-discrete problem at each time level arising from a Backward Euler scheme for a diffusion PDE
$$ u_t = (\alpha(u)u_x)_x + f(u) $$
(\( au \) comes from \( u_t \), \( a\sim 1/\Delta t \), \( f(u) + u^{n-1}/\Delta t \) becomes \( f(u) \) in the model problem)
Finite difference discretizations
The nonlinear term \( (\dfc(u)u^{\prime})^{\prime} \) behaves just as a variable coefficient term \( (\dfc(x)u^{\prime})^{\prime} \) wrt discretization:
$$ [-D_x\dfc D_x u +au = f]_i$$
Written out at internal points:
$$
\begin{align*}
-\frac{1}{\Delta x^2}
\left(\dfc_{i+\half}(u_{i+1}-u_i) -
\dfc_{i-\half}(u_{i}-u_{i-1})\right)
+ au_i &= f(u_i)
\end{align*}
$$
\( \dfc_{i+\half} \): two choices
$$
\begin{align*}
\dfc_{i+\half} &\approx
\dfc(\half(u_i + u_{i+1})) =
[\dfc(\overline{u}^x)]^{i+\half}
\\
\dfc_{i+\half} &\approx
\half(\dfc(u_i) + \dfc(u_{i+1})) = [\overline{\dfc(u)}^x]^{i+\half}
\end{align*}
$$
Finite difference scheme
$$ \dfc_{i+\half} \approx
\half(\dfc(u_i) + \dfc(u_{i+1})) = [\overline{\dfc(u)}^x]^{i+\half} $$
results in
$$ [-D_x\overline{\dfc}^x D_x u +au = f]_i\tp$$
$$
\begin{align*}
&-\frac{1}{2\Delta x^2}
\left((\dfc(u_i)+\dfc(u_{i+1}))(u_{i+1}-u_i) -
(\dfc(u_{i-1})+\dfc(u_{i}))(u_{i}-u_{i-1})\right)\\
&\qquad\qquad + au_i = f(u_i)
\end{align*}
$$
Boundary conditions
- At \( i=N_x \): \( u_i=D \).
- At \( i=0 \): \( \dfc(u)u^{\prime}=C \)
$$ [\dfc(u)D_{2x}u = C]_0$$
$$
\dfc(u_0)\frac{u_{1} - u_{-1}}{2\Delta x} = C
$$
The fictitious value \( u_{-1} \) can, as usual, be eliminated with the aid of the scheme at \( i=0 \)
The structure of the equation system
Structure of nonlinear algebraic equations:
$$ A(u)u = b(u)$$
$$
\begin{align*}
A_{i,i} &= \frac{1}{2\Delta x^2}(\dfc(u_{i-1}) + 2\dfc(u_{i})
+\dfc(u_{i+1})) + a\\
A_{i,i-1} &= -\frac{1}{2\Delta x^2}(\dfc(u_{i-1}) + \dfc(u_{i}))\\
A_{i,i+1} &= -\frac{1}{2\Delta x^2}(\dfc(u_{i}) + \dfc(u_{i+1}))\\
b_i &= f(u_i)
\end{align*}
$$
Note:
- \( A(u) \) is tridiagonal: \( A_{i,j}=0 \) for \( j > 1+1 \) and \( j < i-1 \).
- The \( i=0 \) and \( i=N_x \) equation must incorporate boundary conditions
The equation for the Neumann boundary condition
For \( i=0 \): insert
$$
u_{-1} = u_1 -\frac{2\Delta x}{\dfc(u_0)}
$$
into the numerical scheme, leading to a modified expression
for \( A_{0,0} \). The expression for \( A_{i,i+1} \)
remains the same for \( i=0 \), and \( A_{i,i-1} \) for \( i=0 \) does not enter the system.
The equation for the Dirichlet boundary condition
1. For \( i=N_x \) we can use the Dirichlet condition as a separate equation
$$ u_i = D,\quad i=N_x$$
2. Alternative: we can substitute \( u_{N_x} \) by \( D \) in the numerical scheme for \( i=N_x-1 \) and do not use a seperate equation for \( u_{N_x} \).
Nonlinear equations for a mesh with two cells
Let's do all the details! We omit a separate equation for the \( u=D \) condition at \( i=N_x \). Starting point is then
$$
\begin{align*}
A_{0,-1}u_{-1} + A_{0,0}u_0 + A_{0,1}u_1 &= b_0\\
A_{1,0}u_{0} + A_{1,1}u_1 + A_{1,2}u_2 &= b_1
\end{align*}
$$
Must
- write out the \( A_{i,j} \) and \( b_i \) expressions
- replace \( u_{-1} \) from the Neumann condition
- use \( D \) for \( u_2 \) (boundary condition)
Picard iteration
Use the most recently computed vaue \( u^{-} \) of \( u \) in \( A(u) \) and \( b(u) \):
$$ A(u^{-})u = b(u^{-})$$
$$
\begin{align*}
\frac{1}{2\Delta x^2}(& -(\dfc(u^-_{-1}) + 2\dfc(u^-_{0})
+ \dfc(u^-_{1}))u_1\, +\\
&(\dfc(u^-_{-1}) + 2\dfc(u^-_{0}) + \dfc(u^-_{1}))u_0
+ au_0\\
&=f(u^-_0) -
\frac{1}{\dfc(u^-_0)\Delta x}(\dfc(u^-_{-1}) + \dfc(u^-_{0}))C,
\end{align*}
$$
$$
\begin{align*}
\frac{1}{2\Delta x^2}(&-(\dfc(u^-_{0}) + \dfc(u^-_{1}))u_{0}\, +\\
& (\dfc(u^-_{0}) + 2\dfc(u^-_{1}) + \dfc(D))u_1 + au_1\\
&=f(u^-_1) + \frac{1}{2\Delta x^2}(\dfc(u^-_{1}) + \dfc(D))D\tp
\end{align*}
$$
The matrix systems to be solved
Eliminating the Dirichlet condition at \( i=N_x \):
$$
\left(\begin{array}{cc}
B_{0,0}& B_{0,1}\\
B_{1,0} & B_{1,1}
\end{array}\right)
\left(\begin{array}{c}
u_0\\
u_1
\end{array}\right)
=
\left(\begin{array}{c}
d_0\\
d_1
\end{array}\right)
$$
Including the equation for \( i=N_x \):
$$
\left(\begin{array}{ccc}
B_{0,0}& B_{0,1} & 0\\
B_{1,0} & B_{1,1} & B_{1,2}\\
0 & 0 & 1
\end{array}\right)
\left(\begin{array}{c}
u_0\\
u_1\\
u_2
\end{array}\right)
=
\left(\begin{array}{c}
d_0\\
d_1^{*}\\
D
\end{array}\right)
$$
Newton's method; Jacobian (1)
Nonlinear eq.no \( i \) has the structure
$$
\begin{align*}
F_i &= A_{i,i-1}(u_{i-1},u_i)u_{i-1} +
A_{i,i}(u_{i-1},u_i,u_{i+1})u_i +\\
&\qquad A_{i,i+1}(u_i, u_{i+1})u_{i+1} - b_i(u_i)
\end{align*}
$$
Need Jacobian, i.e., need to differentiate \( F(u)=A(u)u - b(u) \) wrt \( u \). Example:
$$
\begin{align*}
&\frac{\partial}{\partial u_i}(A_{i,i}(u_{i-1},u_i,u_{i+1})u_i) =
\frac{\partial A_{i,i}}{\partial u_i}u_i + A_{i,i}
\frac{\partial u_i}{\partial u_i}\\
&\quad =
\frac{\partial}{\partial u_i}(
\frac{1}{2\Delta x^2}(\dfc(u_{i-1}) + 2\dfc(u_{i})
+\dfc(u_{i+1})) + a)u_i +\\
&\qquad\frac{1}{2\Delta x^2}(\dfc(u_{i-1}) + 2\dfc(u_{i})
+\dfc(u_{i+1})) + a\\
&\quad =\frac{1}{2\Delta x^2}(2\dfc^\prime (u_i)u_i
+\dfc(u_{i-1}) + 2\dfc(u_{i})
+\dfc(u_{i+1})) + a
\end{align*}
$$
Newton's method; Jacobian (2)
The complete Jacobian becomes (make sure you get this!)
$$
\begin{align*}
J_{i,i} &= \frac{\partial F_i}{\partial u_i}
= \frac{\partial A_{i,i-1}}{\partial u_i}u_{i-1}
+ \frac{\partial A_{i,i}}{\partial u_i}u_i
+ A_{i,i}
+ \frac{\partial A_{i,i+1}}{\partial u_i}u_{i+1}
- \frac{\partial b_i}{\partial u_{i}}\\
&=
\frac{1}{2\Delta x^2}(
-\dfc^{\prime}(u_i)u_{i-1}
+2\dfc^{\prime}(u_i)u_{i}
+\dfc(u_{i-1}) + 2\dfc(u_i) + \dfc(u_{i+1})) +\\
&\quad a
-\frac{1}{2\Delta x^2}\dfc^{\prime}(u_{i})u_{i+1}
- b^{\prime}(u_i)\\
J_{i,i-1} &= \frac{\partial F_i}{\partial u_{i-1}}
= \frac{\partial A_{i,i-1}}{\partial u_{i-1}}u_{i-1}
+ A_{i-1,i}
+ \frac{\partial A_{i,i}}{\partial u_{i-1}}u_i
- \frac{\partial b_i}{\partial u_{i-1}}\\
&=
\frac{1}{2\Delta x^2}(
-\dfc^{\prime}(u_{i-1})u_{i-1} - (\dfc(u_{i-1}) + \dfc(u_i))
+ \dfc^{\prime}(u_{i-1})u_i)\\
J_{i,i+1} &= \frac{\partial A_{i,i+1}}{\partial u_{i-1}}u_{i+1}
+ A_{i+1,i} +
\frac{\partial A_{i,i}}{\partial u_{i+1}}u_i
- \frac{\partial b_i}{\partial u_{i+1}}\\
&=\frac{1}{2\Delta x^2}(
-\dfc^{\prime}(u_{i+1})u_{i+1} - (\dfc(u_{i}) + \dfc(u_{i+1}))
+ \dfc^{\prime}(u_{i+1})u_i)
\end{align*}
$$
Newton's method; nonlinear equations at the end points
$$
\begin{align*}
F_i &= -\frac{1}{2\Delta x^2}
((\dfc(u_i)+\dfc(u_{i+1}))(u_{i+1}-u_i) -
(\dfc(u_{i-1})+\dfc(u_{i}))\times \\
&\qquad (u_{i}-u_{i-1})) + au_i - f(u_i) = 0
\end{align*}
$$
At \( i=0 \), replace \( u_{-1} \) by formula from Neumann condition.
- Exclude Dirichlet condition as separate equation: replace \( u_i \), \( i=N_x \), by \( D \) in \( F_{i} \), \( i=N_x-1 \)
- Include Dirichlet condition as separate equation:
$$ F_{N_x}(u_0,\ldots,u_{N_x}) = u_{N_x} - D = 0\tp$$
Note: The size of the Jacobian depends on 1 or 2.
Galerkin-type discretizations
- \( V \): function space with basis functions \( \baspsi_i(x) \), \( i\in\If \)
- Dirichlet conditionat \( x=L \): \( \baspsi_i(L)=0 \), \( i\in\If \) (\( v(L)=0\ \forall v\in V \))
- \( u = D + \sum_{j\in\If}c_j\baspsi_j \)
Galerkin's method for \( -(\dfc(u)u')' + au = f(u) \):
$$
\int_0^L \dfc(u)u^{\prime}v^{\prime}\dx + \int_0^L auv\dx =
\int_0^L f(u)v\dx + [\dfc(u)u^{\prime}v]_0^L,\quad \forall v\in V
$$
Insert Neumann condition:
$$ [\dfc(u)u^{\prime}v]_0^L = \dfc(u(L))u^{\prime}(L)v(L) - \dfc(u(0))u^{\prime}(0)v(0)
= -Cv(0)
$$
The nonlinear algebraic equations
Find \( u\in V \) such that
$$
\int_0^L \dfc(u)u^{\prime}v^{\prime}\dx + \int_0^L auv\dx =
\int_0^L f(u)v\dx - Cv(0),\quad \forall v\in V
$$
\( \forall v\in V\ \Rightarrow\ \forall i\in\If \), \( v=\baspsi_i \). Inserting \( u=D+\sum_jc_j\baspsi_j \) and sorting terms:
$$
\sum_{j}\left(
\int\limits_0^L \left(\dfc(D+\sum_{k}c_k\baspsi_k)
\baspsi_j^{\prime}\baspsi_i^{\prime} + a \baspsi_j\baspsi_i\right)\dx\right)c_j =
\int\limits_0^L f(D+\sum_{k}c_k\baspsi_k)\baspsi_i\dx -
C\baspsi_i(0)
$$
This is a nonlinear algebraic system
Fundamental integration problem: how to deal with \( \int f(\sum_kc_k\baspsi_k)\baspsi_idx \) for unknown \( c_k \)?
- We do not know \( c_k \) in \( \int_0^L f(\sum_kc_k\baspsi_k)\baspsi_i dx \) and \( \int_0^L \dfc(\sum_{k}c_k\baspsi_k)\baspsi_i^{\prime}\baspsi_j^{\prime}\dx \)
- Solution: numerical integration with approximations to \( c_k \), as in \( \int_0^L f(u^{-})\baspsi_idx \)
We choose \( \baspsi_i \) as finite element basis functions
$$ \baspsi_i = \basphi_{\nu(i)},\quad i\in\If$$
Degree of freedom number \( \nu(i) \) in the mesh corresponds to unknown number \( i \) (\( c_i \)).
Model problem: \( \nu(i)=i \), \( \If=\{0,\ldots,N_n-2\} \) (last node excluded)
$$ u = D + \sum_{j\in\If} c_j\basphi_{\nu(j)}$$
or with \( \basphi_i \) in the boundary function:
$$ u = D\basphi_{N_n-1} + \sum_{j\in\If} c_j\basphi_{j}$$
The group finite element method
Since \( u \) is represented by \( \sum_j\basphi_j u(\xno{j}) \), we may use the same approximation for \( f(u) \):
$$
f(u)\approx \sum_{j} f(\xno{j})\basphi_j
$$
\( f(\xno{j}) \): value of \( f \) at node \( j \). With \( u_j \) as \( u(\xno{j}) \), we can write
$$
f(u)\approx \sum_{j} f(u_{j})\basphi_j
$$
This approximation is known as the group finite element method or the product approximation technique. The index \( j \) runs over all node numbers in the mesh.
What is the point with the group finite element method?
- Complicated nonlinear expressions can be simplified to increase the efficiency of numerical computations.
- One can derive symbolic forms of the difference equations arising from the finite element method in nonlinear problems. The symbolic form is useful for comparing finite element and finite difference equations of nonlinear differential equation problems.
Simplified problem for symbolic calculations
Simple nonlinear problem: \( -u^{\prime\prime}=u^2 \), \( u'(0)=1 \), \( u'(L)=0 \).
$$ \int_0^L u^{\prime}v^{\prime}\dx = \int_0^L u^2v\dx
- v(0),\quad\forall v\in V$$
Now,
- Focus on \( \int u^2v\dx \)
- Set \( c_j = u(\xno{j}) = u_j \)
(to mimic finite difference interpretation of \( u_j \)) - That is, \( u = \sum_ju_j\basphi_j \)
Integrating very simple nonlinear functions results in complicated expressions in the finite element method
Consider \( \int u^2v\dx \) with \( u = \sum_ku_k\basphi_k \) and \( v=\basphi_i \):
$$ \int_0^L (\sum_ku_k\basphi_k)^2\basphi_i\dx$$
Tedious exact evaluation on uniform P1 elements:
$$ \frac{h}{12}(u_{i-1}^2 + 2u_i(u_{i-1} + u_{i+1}) + 6u_i^2
+ u_{i+1}^2)$$
Finite difference counterpart: \( u_i^2 \) (!)
Application of the group finite element method
$$ \int_0^L f(u)\basphi_i\dx \approx
\int_0^L (\sum_j \basphi_jf(u_j))\basphi_i\dx
= \sum_j (\underbrace{\int_0^L \basphi_i\basphi_j\dx}_{\mbox{mass matrix }M_{i,j}}) f(u_j)$$
Corresponding part of difference equation for P1 elements:
$$ \frac{h}{6}(f(u_{i-1}) + 4f(u_i) + f(u_{i+1}))$$
Rewrite as "finite difference form plus something":
$$ \frac{h}{6}(f(u_{i-1}) + 4f(u_i) + f(u_{i+1}))
= h[{\color{red}f(u)} - \frac{h^2}{6}D_xD_x f(u)]_i$$
This is like the finite difference discretization of \( -u'' = f(u) - \frac{h^2}{6}f''(u) \)
Lumping the mass matrix gives finite difference form
Alternative: evaluation of finite element terms at nodes gives great simplifications
Idea: integrate \( \int f(u)v\dx \) numerically with a rule that samples \( f(u)v \) at the nodes only. This involves great simplifications, since
$$ \sum_k u_k\basphi_k(\xno{\ell}) = u_\ell$$
and
$$ f\basphi_i(\xno{\ell}) =
f(\sum_k u_k\underbrace{\basphi_k(\xno{\ell})}_{\delta_{k\ell}})
\underbrace{\basphi_i(\xno{\ell})}_{\delta_{i\ell}}
= f(u_\ell)\delta_{i\ell}\quad \neq 0\mbox{ only for } f(u_i)$$
(\( \delta_{ij}=0 \) if \( i\neq j \) and \( \delta_{ij}=1 \) if \( i=j \))
Numerical integration of nonlinear terms
Trapezoidal rule with the nodes only gives the finite difference form of \( [f(u)]_i \):
$$
\int_0^L f(\sum_k u_k\basphi_k)(x)\basphi_i(x)\dx
\approx h\sum_{\ell=0}^{N_n-1} f(u_\ell)\delta_{i\ell} - \mathcal{C}
= h{\color{red}f(u_i)}
$$
(\( \mathcal{C} \): boundary adjustment of rule, \( i=0,N_n-1 \))
Finite elements for a variable coefficient Laplace term
Consider the term \( (\dfc u^{\prime})^{\prime} \), with the group finite element method: \( \dfc(u)\approx \sum_k\alpha(u_k)\basphi_k \), and the variational counterpart
$$
\int_0^L \dfc(\sum_k c_k\basphi_k)\basphi_i^{\prime}\basphi_j^{\prime}\dx
\approx
\sum_k (\int_0^L \basphi_k\basphi_i^{\prime}\basphi_j^{\prime}\dx)
\dfc(u_k) = \ldots
$$
Further calculations (see text) lead to
$$
-\frac{1}{h}(\half(\dfc(u_i) + \dfc(u_{i+1}))(u_{i+1}-u_i)
- \half(\dfc(u_{i-1}) + \dfc(u_{i}))(u_{i}-u_{i-1}))
$$
= standard finite difference discretization of \( -(\dfc(u)u^{\prime})^{\prime} \) with an arithmetic mean of \( \dfc(u) \)
Numerical integration at the nodes
Instead of the group finite element method and exact integration, use Trapezoidal rule in the nodes for \( \int_0^L \dfc(\sum_k u_k\basphi_k)\basphi_i^{\prime}\basphi_j^{\prime}\dx \).
Work at the cell level (most convenient with discontinuous \( \basphi_i' \)):
$$
\begin{align*}
& \int_{-1}^1 \alpha(\sum_t\tilde u_t\refphi_t)\refphi_r'\refphi_s'\frac{h}{2}dX
= \int_{-1}^1 \dfc(\sum_{t=0}^1
\tilde u_t\refphi_t)\frac{2}{h}\frac{d\refphi_r}{dX}
\frac{2}{h}\frac{d\refphi_s}{dX}\frac{h}{2}dX\\
&\quad = \frac{1}{2h}(-1)^r(-1)^s \int_{-1}^1 \dfc(\sum_{t=0}^1 u_t\refphi_t(X))dX
\\
& \qquad \approx \frac{1}{2h}(-1)^r(-1)^s\dfc (
\sum_{t=0}^1\refphi_t(-1)\tilde u_t) + \dfc(\sum_{t=0}^1\refphi_t(1)\tilde u_t)\\
&\quad = \frac{1}{2h}(-1)^r(-1)^s(\dfc(\tilde u_0) + \dfc(\tilde u^{(1)}))
\end{align*}
$$
Summary of finite element vs finite difference nonlinear algebraic equations
$$ -(\dfc(u)u^{\prime})^{\prime} +au = f(u)$$
Uniform P1 finite elements:
- Group finite element or Trapezoidal integration at nodes:
\( -(\dfc(u)u^{\prime})^{\prime} \) becomes \( -h[D_x\overline{\dfc(u)}^xD_x u]_i \) - \( f(u) \) becomes \( hf(u_i) \) with Trapezoidal integration
or the "mass matrix" representation \( h[f(u) - \frac{h}{6}D_xD_x f(u)]_i \) if group finite elements - \( au \) leads to the "mass matrix" form \( ah[u - \frac{h}{6}D_xD_x u]_i \)
Real computations utilize accurate numerical integration
- Previous group finite element or Trapezoidal integration examples had one aim: derive symbolic expressions for finite element equations
- Real world computations apply numerical integration
- How to define Picard iteration and Newton's method from a variational form with numerical integration in real world computations?
Picard iteration defined from the variational form
$$
-(\dfc(u)u^{\prime})^{\prime} + au = f(u),\quad x\in (0,L),
\quad \dfc(u(0))u^{\prime}(0) = C,\ u(L)=D
$$
Variational form (\( v=\baspsi_i \)):
$$
F_i =
\int_0^L \dfc(u)u^{\prime}\baspsi_i^{\prime}\dx + \int_0^L au\baspsi_i\dx -
\int_0^L f(u)\baspsi_i\dx + C\baspsi_i(0) = 0
$$
Picard iteration: use "old value" \( u^{-} \) in \( \dfc(u) \) and \( f(u) \) and integrate numerically:
$$
F_i = \int_0^L (\dfc(u^{-})u^{\prime}\baspsi_i^{\prime} + au\baspsi_i)\dx -
\int_0^L f(u^{-})\baspsi_i\dx + C\baspsi_i(0)
$$
The linear system in Picard iteration
$$
F_i = \int_0^L (\dfc(u^{-})u^{\prime}\baspsi_i^{\prime} + au\baspsi_i)\dx -
\int_0^L f(u^{-})\baspsi_i\dx + C\baspsi_i(0)
$$
This is a linear problem \( a(u,v)=L(v) \) with bilinear and linear forms
$$ a(u,v) = \int_0^L (\dfc(u^{-})u^{\prime}v^{\prime} + auv)\dx,\quad
L(v) = \int_0^L f(u^{-})v\dx - Cv(0)$$
The linear system now is computed the standard way.
The equations in Newton's method
$$
F_i =
\int_0^L (\dfc(u)u^{\prime}\baspsi_i^{\prime} + au\baspsi_i -
f(u)\baspsi_i)\dx + C\baspsi_i(0)=0,\quad i\in\If
$$
Easy to evaluate right-hand side \( -F_i(u^{-}) \) by numerical integration:
$$
F_i =
\int_0^L (\dfc(u^{-})u^{\prime}\baspsi_i^{\prime} + au\baspsi_i -
f(u^{-})\baspsi_i)\dx + C\baspsi_i(0)=0
$$
(just known functions)
Useful formulas for computing the Jacobian
$$
\begin{align*}
\frac{\partial u}{\partial c_j} &= \frac{\partial}{\partial c_j}
\sum_kc_k\baspsi_k = \baspsi_j\\
\frac{\partial u^{\prime}}{\partial c_j} &= \frac{\partial}{\partial c_j}
\sum_kc_k\baspsi_k^{\prime} = \baspsi_j^{\prime}
\end{align*}
$$
Computing the Jacobian
$$
\begin{align*}
J_{i,j} = \frac{\partial F_i}{\partial c_j}
& = \int_0^L \frac{\partial}{\partial c_j}
(\dfc(u)u^{\prime}\baspsi_i^{\prime} + au\baspsi_i -
f(u)\baspsi_i)\dx\\
&=
\int_0^L
((\dfc^{\prime}(u)\frac{\partial u}{\partial c_j}u^{\prime} +
\dfc(u)\frac{\partial u^{\prime}}{\partial c_j})\baspsi_i^{\prime}
+ a\frac{\partial u}{\partial c_j}\baspsi_i -
f^{\prime}(u)\frac{\partial u}{\partial c_j}\baspsi_i)\dx\\
&=
\int_0^L
((\dfc^{\prime}(u)\baspsi_ju^{\prime} +
\dfc(u)\baspsi_j^{\prime}\baspsi_i^{\prime}
+ a\baspsi_j\baspsi_i -
f^{\prime}(u)\baspsi_j\baspsi_i)\dx\\
&=
\int_0^L
(\dfc^{\prime}(u)u^{\prime}\baspsi_i^{\prime}\baspsi_j +
\dfc(u)\baspsi_i^{\prime}\baspsi_j^{\prime}
+ (a - f^{\prime}(u))\baspsi_i\baspsi_j)\dx
\end{align*}
$$
Use \( \dfc^{\prime}(u^{-}) \), \( \dfc(u^{-}) \), \( f^\prime (u^{-}) \), \( f(u^{-}) \) and integrate expressions numerically (only known functions)
Computations in a reference cell \( [-1,1] \)
$$
\begin{align*}
\tilde F_r^{(e)} &=
\int_{-1}^1\left(
\dfc(\tilde u^{-})\tilde u^{-\prime}\refphi_r^{\prime} +
(a \tilde u^{-}-f(\tilde u^{-}))\refphi_r\right)\det J\dX -
C\refphi_r(0)
\\
\tilde J_{r,s}^{(e)} &=
\int_{-1}^1
(\dfc^{\prime}(\tilde u^{-})\tilde u^{-\prime}\refphi_r^{\prime}\refphi_s +
\dfc(\tilde u^{-})\refphi_r^{\prime}\refphi_s^{\prime}
+ (a - f^{\prime}(\tilde u^{-}))\refphi_r\refphi_s)\det J\dX
\end{align*}
$$
\( r,s\in\Ifd \) (local degrees of freedom)
How to handle Dirichlet conditions in Newton's method
- Newton's method solves \( J(u^{-})\delta u = -F(u^{-}) \)
- \( \delta u \) is a correction to \( u^{-} \)
- If \( u(\xno{i}) \) has Dirchlet condition \( D \), set \( u^{-}_i=D \) in prior to the first iteration
- Set \( \delta u_i=0 \) (no change for Dirichlet conditions)
Multi-dimensional PDE problems
$$
u_t = \nabla\cdot(\dfc(u)\nabla u) + f(u)
$$
Backward Euler and variational form
$$
u_t = \nabla\cdot(\dfc(u)\nabla u) + f(u)
$$
Backward Euler time discretization:
$$ u^n - \Delta t\nabla\cdot(\dfc(u^n)\nabla u^n) - \Delta t f(u^n) = u^{n-1}$$
Alternative notation (\( u \) for \( u^n \), \( u^{(1)} \) for \( u^{n-1} \)):
$$ u - \Delta t\nabla\cdot(\dfc(u)\nabla u) - \Delta t f(u) = u^{(1)}$$
Boundary conditions: \( \partial u/\partial n=0 \) for simplicity. Variational form:
$$
\int_\Omega (uv + \Delta t\,\dfc(u)\nabla u\cdot\nabla v
- \Delta t f(u)v - u^{(1)} v)\dx = 0
$$
Nonlinear algebraic equations arising from the variational form
$$
\int_\Omega (uv + \Delta t\,\dfc(u)\nabla u\cdot\nabla v
- \Delta t f(u)v - u^{(1)} v)\dx = 0
$$
$$
F_i =
\int_\Omega (u\baspsi_i + \Delta t\,\dfc(u)\nabla u\cdot\nabla \baspsi_i
- \Delta t f(u)\baspsi_i - u^{(1)}\baspsi_i)\dx = 0
$$
Picard iteration:
$$
F_i \approx \hat F_i =
\int_\Omega (u\baspsi_i + \Delta t\,\dfc(u^{-})\nabla u\cdot\nabla \baspsi_i
- \Delta t f(u^{-})\baspsi_i - u^{(1)}\baspsi_i)\dx = 0
$$
This is a variable coefficient problem like \( au - \nabla\cdot\dfc(\x)\nabla u = f(\x,t) \) and results in a linear system
A note on our notation and the different meanings of \( u \) (1)
PDE problem: \( u(\x,t) \) is the exact solution of
$$
u_t = \nabla\cdot(\dfc(u)\nabla u) + f(u)
$$
Time discretization: \( u(\x) \) is the exact solution of the time-discrete spatial equation
$$ u - \Delta t\nabla\cdot(\dfc(u^n)\nabla u) - \Delta t f(u) = u^{(1)}$$
The same \( u(\x) \) is the exact solution of the (continuous) variational form:
$$
\int_\Omega (uv + \Delta t\,\dfc(u)\nabla u\cdot\nabla v
- \Delta t f(u)v - u^{(1)} v)\dx,\quad\forall v\in V
$$
A note on our notation and the different meanings of \( u \) (2)
Or we may approximate \( u \): \( u(\x) = \sum_jc_j\baspsi_j(\x) \) and let this spatially discrete \( u \) enter the variational form,
$$
\int_\Omega (uv + \Delta t\,\dfc(u)\nabla u\cdot\nabla v
- \Delta t f(u)v - u^{(1)} v)\dx,\quad\forall v\in V
$$
Picard iteration: \( u(\x) \) solves the approximate variational form
$$
\int_\Omega (uv + \Delta t\,\dfc(u^{-})\nabla u\cdot\nabla v
- \Delta t f(u^{-})v - u^{(1)} v)\dx
$$
Could introduce
- \( \uex(\x,t) \) for the exact solution of the PDE problem
- \( \uex(\x)^n \) for the exact solution after time discretization
- \( u^n(\x) \) for the spatially discrete solution \( \sum_jc_j\baspsi_j \)
- \( u^{n,k} \) for approximation in Picard/Newton iteration no \( k \) to \( u^n(\x) \)
Newton's method (1)
Need to evaluate \( F_i(u^{-}) \):
$$
F_i \approx \hat F_i =
\int_\Omega (u^{-}\baspsi_i + \Delta t\,\dfc(u^{-})
\nabla u^{-}\cdot\nabla \baspsi_i
- \Delta t f(u^{-})\baspsi_i - u^{(1)}\baspsi_i)\dx
$$
To compute the Jacobian we need
$$
\begin{align*}
\frac{\partial u}{\partial c_j} &= \sum_k\frac{\partial}{\partial c_j}
c_k\baspsi_k = \baspsi_j\\
\frac{\partial \nabla u}{\partial c_j} &= \sum_k\frac{\partial}{\partial c_j}
c_k\nabla \baspsi_k = \nabla \baspsi_j
\end{align*}
$$
Newton's method (2)
The Jacobian becomes
$$
\begin{align*}
J_{i,j} = \frac{\partial F_i}{\partial c_j} =
\int_\Omega & (\baspsi_j\baspsi_i + \Delta t\,\dfc^{\prime}(u)\baspsi_j
\nabla u\cdot\nabla \baspsi_i +
\Delta t\,\dfc(u)\nabla\baspsi_j\cdot\nabla\baspsi_i - \\
&\ \Delta t f^{\prime}(u)\baspsi_j\baspsi_i)\dx
\end{align*}
$$
Evaluation of \( J_{i,j} \) as the coefficient matrix in the Newton system \( J\delta u = -F \) means \( J(u^{-}) \):
$$
\begin{align*}
J_{i,j} =
\int_\Omega & (\baspsi_j\baspsi_i + \Delta t\,\dfc^{\prime}(u^{-})\baspsi_j
\nabla u^{-}\cdot\nabla \baspsi_i +
\Delta t\,\dfc(u^{-})\nabla\baspsi_j\cdot\nabla\baspsi_i - \\
&\ \Delta t f^{\prime}(u^{-})\baspsi_j\baspsi_i)\dx
\end{align*}
$$
Non-homogeneous Neumann conditions
A natural physical flux condition:
$$
-\dfc(u)\frac{\partial u}{\partial n} = g,\quad\x\in\partial\Omega_N
$$
Integration by parts gives the boundary term
$$
\int_{\partial\Omega_N}\dfc(u)\frac{\partial u}{\partial u}v\ds
$$
Inserting the nonlinear Neumann condition:
$$ -\int_{\partial\Omega_N}gv\ds$$
(no nonlinearity)
Robin condition
Heat conduction problems often apply a kind of Newton's cooling law, also known as a Robin condition, at the boundary:
$$
-\dfc(u)\frac{\partial u}{\partial u} = h(u)(u-T_s(t)),\quad\x\in\partial\Omega_R
$$
Here:
- \( h(u) \): heat transfer coefficient between the body (\( \Omega \)) and its surroundings
- \( T_s \): temperature of the surroundings
Inserting the condition in the boundary integral \( \int_{\partial\Omega_N}\dfc(u)\frac{\partial u}{\partial u}v\ds \):
$$ \int_{\partial\Omega_R}h(u)(u-T_s(T))v\ds$$
Use \( h(u^{-})(u-T_s) \) for Picard, differentiate for Newton
Finite difference discretization in a 2D problem
$$ u_t = \nabla\cdot(\dfc(u)\nabla u) + f(u)$$
Backward Euler in time, centered differences in space:
$$ [D_t^- u = D_x\overline{\dfc(u)}^xD_x u
+ D_y\overline{\dfc(u)}^yD_y u + f(u)]_{i,j}^n
$$
$$
\begin{align*}
u^n_{i,j} &- \frac{\Delta t}{h^2}(
\half(\dfc(u_{i,j}^n) + \dfc(u_{i+1,j}^n))(u_{i+1,j}^n-u_{i,j}^n)\\
&\quad -
\half(\dfc(u_{i-1,j}^n) + \dfc(u_{i,j}^n))(u_{i,j}^n-u_{i-1,j}^n) \\
&\quad +
\half(\dfc(u_{i,j}^n) + \dfc(u_{i,j+1}^n))(u_{i,j+1}^n-u_{i,j}^n)\\
&\quad -
\half(\dfc(u_{i,j-1}^n) + \dfc(u_{i,j}^n))(u_{i,j}^n-u_{i-1,j-1}^n))
- \Delta tf(u_{i,j}^n) = u^{n-1}_{i,j}
\end{align*}
$$
Nonlinear algebraic system on the form \( A(u)u=b(u) \)
Picard iteration
- Use the most recently computed values \( u^{-} \) of \( u^n \) in \( \dfc \) and \( f \)
- Or: \( A(u^{-})u=b(u^{-}) \)
- Like solving \( u_t = \nabla\cdot (\dfc(\x)\nabla u) + f(\x,t) \)
Picard iteration in operator notation:
$$ [D_t^- u = D_x\overline{\dfc(u^{-})}^xD_x u
+ D_y\overline{\dfc(u^{-})}^yD_y u + f(u^{-})]_{i,j}^n
$$
Newton's method: the nonlinear algebraic equations
Define the nonlinear equations (use \( u \) for \( u^n \), \( u^{(1)} \) for \( u^{n-1} \)):
$$
\begin{align*}
F_{i,j} &= u_{i,j} - \frac{\Delta t}{h^2}(\\
&\qquad \half(\dfc(u_{i,j}) + \dfc(u_{i+1,j}))(u_{i+1,j}-u_{i,j}) -\\
&\qquad \half(\dfc(u_{i-1,j}) + \dfc(u_{i,j}))(u_{i,j}-u_{i-1,j}) + \\
&\qquad \half(\dfc(u_{i,j}) + \dfc(u_{i,j+1}))(u_{i,j+1}-u_{i,j}) -\\
&\qquad \half(\dfc(u_{i,j-1}) + \dfc(u_{i,j}))(u_{i,j}-u_{i-1,j-1})) -
\Delta t\, f(u_{i,j}) - u^{(1)}_{i,j} = 0
\end{align*}
$$
Newton's method: the Jacobian and its sparsity
$$ J_{i,j,r,s} = \frac{\partial F_{i,j}}{\partial u_{r,s}} $$
Newton system:
$$ \sum_{r\in\Ix}\sum_{s\in\Iy}J_{i,j,r,s}\delta u_{r,s} = -F_{i,j},
\quad i\in\Ix,\ j\in\Iy\tp$$
But \( F_{i,j} \) contains only \( u_{i\pm 1,j} \), \( u_{i,j\pm 1} \), and \( u_{i,j} \). We get nonzero contributions only for \( J_{i,j,i-1,j} \), \( J_{i,j,i+1,j} \), \( J_{i,j,i,j-1} \), \( J_{i,j,i,j+1} \), and \( J_{i,j,i,j} \). The Newton system collapses to
$$
\begin{align*}
J_{i,j,r,s}\delta u_{r,s} =
J_{i,j,i,j}\delta u_{i,j} & +
J_{i,j,i-1,j}\delta u_{i-1,j} +\\
& J_{i,j,i+1,j}\delta u_{i+1,j} +
J_{i,j,i,j-1}\delta u_{i,j-1}
+ J_{i,j,i,j+1}\delta u_{i,j+1}
\end{align*}
$$
Newton's method: details of the Jacobian
$$
\begin{align*}
J_{i,j,i-1,j} &= \frac{\partial F_{i,j}}{\partial u_{i-1,j}}\\
&= \frac{\Delta t}{h^2}(\dfc^{\prime}(u_{i-1,j})(u_{i,j}-u_{i-1,j})
+ \dfc(u_{i-1,j})(-1)),\\
J_{i,j,i+1,j} &= \frac{\partial F_{i,j}}{\partial u_{i+1,j}}\\
&= \frac{\Delta t}{h^2}(-\dfc^{\prime}(u_{i+1,j})(u_{i+1,j}-u_{i,j})
- \dfc(u_{i-1,j})),\\
J_{i,j,i,j-1} &= \frac{\partial F_{i,j}}{\partial u_{i,j-1}}\\
&= \frac{\Delta t}{h^2}(\dfc^{\prime}(u_{i,j-1})(u_{i,j}-u_{i,j-1})
+ \dfc(u_{i,j-1})(-1)),\\
J_{i,j,i,j+1} &= \frac{\partial F_{i,j}}{\partial u_{i,j+1}}\\
&= \frac{\Delta t}{h^2}(-\dfc^{\prime}(u_{i,j+1})(u_{i,j+1}-u_{i,j})
- \dfc(u_{i,j-1}))\tp
\end{align*}
$$
Good exercise at this point: \( J_{i,j,i,j} \)
Compute \( J_{i,j,i,j} \):
$$
\begin{align*}
F_{i,j} &= u_{i,j} - \frac{\Delta t}{h^2}(\\
&\qquad \half(\dfc(u_{i,j}) + \dfc(u_{i+1,j}))(u_{i+1,j}-u_{i,j}) -\\
&\qquad \half(\dfc(u_{i-1,j}) + \dfc(u_{i,j}))(u_{i,j}-u_{i-1,j}) + \\
&\qquad \half(\dfc(u_{i,j}) + \dfc(u_{i,j+1}))(u_{i,j+1}-u_{i,j}) -\\
&\qquad \half(\dfc(u_{i,j-1}) + \dfc(u_{i,j}))(u_{i,j}-u_{i-1,j-1})) -
\Delta t\, f(u_{i,j}) - u^{(1)}_{i,j} = 0\\
J_{i,j,i,j} &= \frac{\partial F_{i,j}}{\partial u_{i,j}}
\end{align*}
$$
Continuation methods
- Picard iteration or Newton's method may diverge
- Relaxation with \( \omega < 1 \) may help
- If not, resort to continuation methods
Continuation method: solve difficult problem as a sequence of simpler problems
- Introduce a continuation parameter \( \Lambda \)
- \( \Lambda =0 \): simple version of the PDE problem
- \( \Lambda =1 \): desired PDE problem
- Increase \( \Lambda \) in steps: \( \Lambda_0=0 ,\Lambda_1 < \cdots < \Lambda_n=1 \)
- Use the solution from \( \Lambda_{i-1} \) as initial guess for the iterations for \( \Lambda_i \)
Example on a continuation method
$$ -\nabla\cdot\left( ||\nabla u||^q\nabla u\right) = f, $$
Pseudo-plastic fluids may be \( q=-0.8 \), which is a difficult problem for Picard/Newton iteration.
$$ \Lambda\in [0,1]:\quad q=-\Lambda 0.8 $$
$$
-\nabla\cdot\left( ||\nabla u||^{-\Lambda 0.8}\nabla u\right) = f$$
Start with \( \Lambda = 0 \), increase in steps to \( \Lambda =1 \), use previous solution as initial guess for Newton or Picard