The 1D diffusion equation
The initial-boundary value problem for 1D diffusion
Step 1: Discretizing the domain
The discrete solution
Step 2: Fulfilling the equation at the mesh points
Step 3: Replacing derivatives by finite differences
Step 4: Formulating a recursive algorithm
The mesh Fourier number
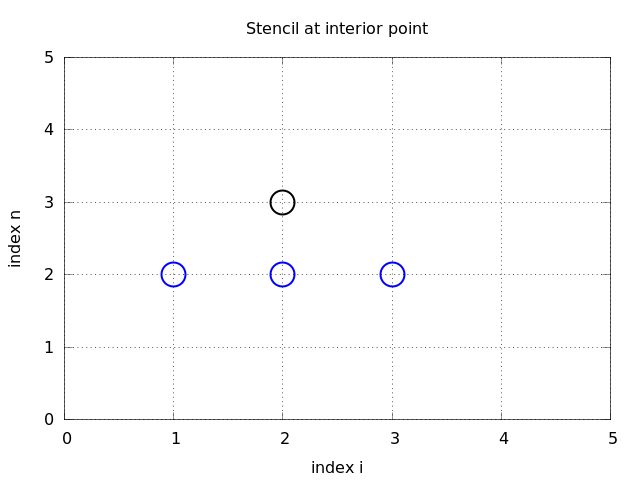
The finite difference stencil
The computational algorithm for the Forward Euler scheme
The Python implementation of the computational algorithm
Moving finite difference stencil
Demo program
Forward Euler applied to an initial plug profile
Forward Euler applied to a Gaussian profile
Backward Euler scheme
Let's write out the equations for \( N_x=3 \)
Two classes of discretization methods: explicit and implicit
The linear system for a general \( N_x \)
\( A \) is very sparse: a tridiagonal matrix
Detailed expressions for the matrix entries
The right-hand side
Naive Python implementation with a dense \( (N_x+1)\times(N_x+1) \) matrix
A sparse matrix representation will dramatically reduce the computational complexity
Computing the sparse matrix
Backward Euler applied to a plug profile
Backward Euler applied to a Gaussian profile
Crank-Nicolson scheme
Averaging in time is necessary in the Crank-Nicolson scheme
Crank-Nicolsoon scheme written out
Crank-Nicolson applied to a plug profile
Crank-Nicolson applied to a Gaussian profile
The \( \theta \) rule
The Laplace and Poisson equation
We can solve 1D Poisson/Laplace equation by going to infinity in time-dependent diffusion equations
Extensions
Analysis of schemes for the diffusion equation
Properties of the solution
Example
High frequency components of the solution are very quickly damped
Damping of a discontinuity; problem
Damping of a discontinuity; model
Damping of a discontinuity; Backward Euler scheme
Damping of a discontinuity; Backward Euler simulation \( F=\half \)
Damping of a discontinuity; Forward Euler scheme
Damping of a discontinuity; Forward Euler simulation \( F=\half \)
Damping of a discontinuity; Crank-Nicolson scheme
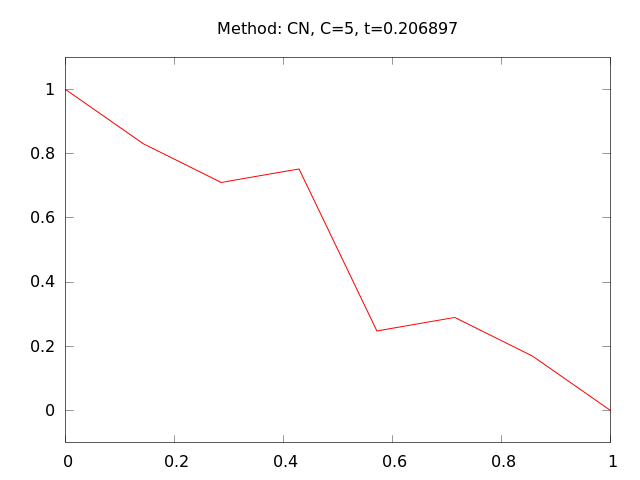
Damping of a discontinuity; Crank-Nicolson simulation \( F=5 \)
Fourier representation
Analysis of the finite difference schemes
Analysis of the Forward Euler scheme
Results for stability
Analysis of the Backward Euler scheme
Analysis of the Crank-Nicolson scheme
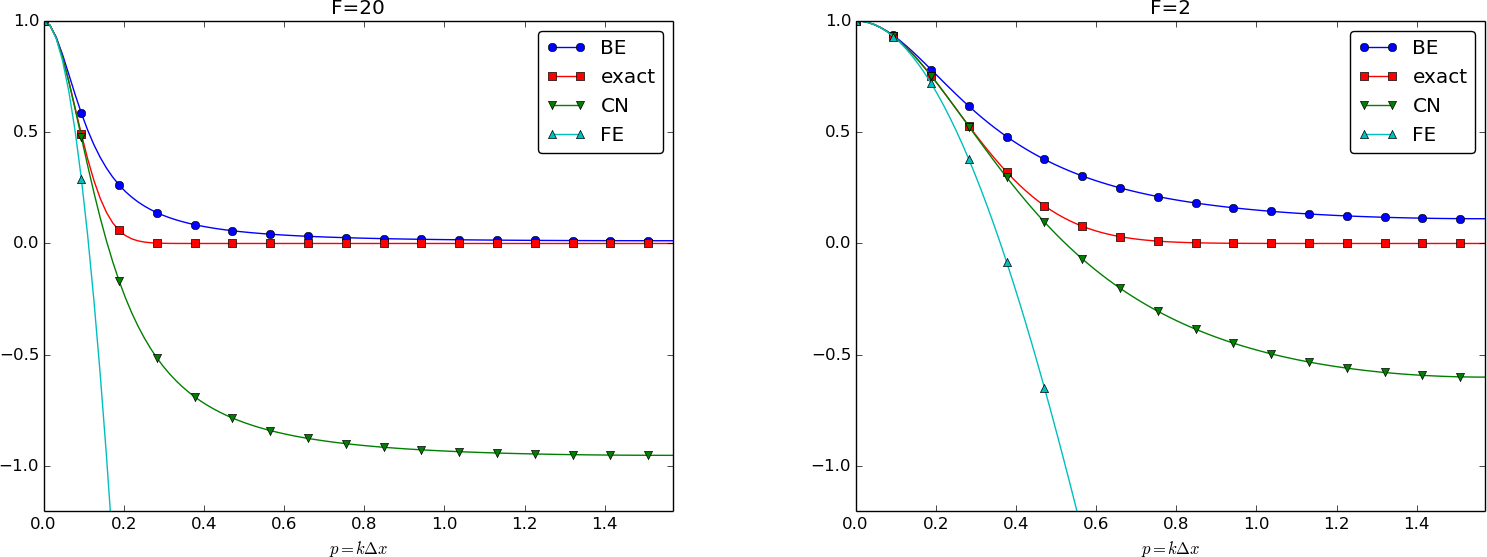
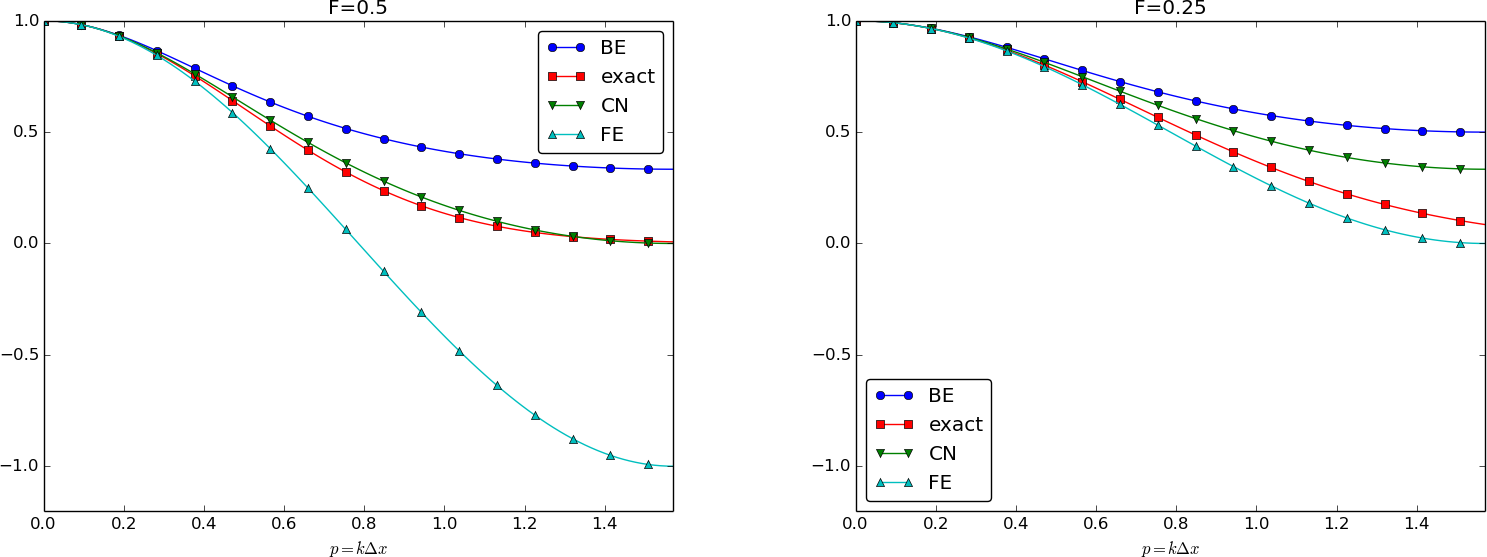
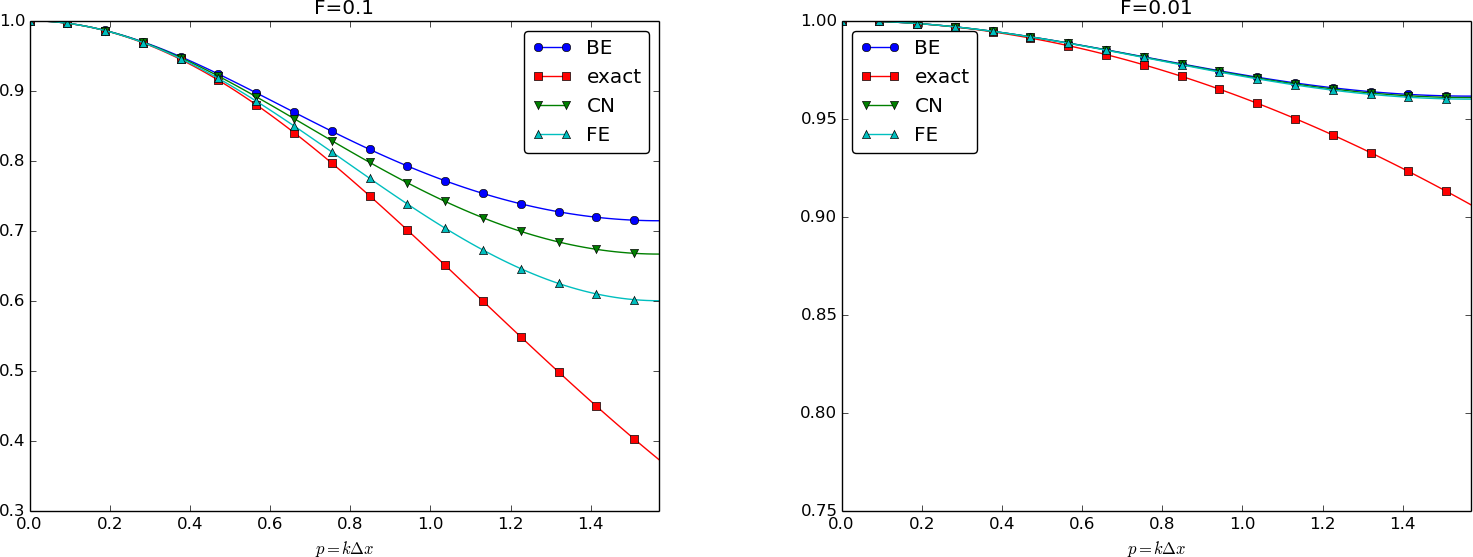
Summary of amplification factors
Summary of accuracy of amplification factors; large time steps
Summary of accuracy of amplification factors; time steps around the Forward Euler stability limit
Summary of accuracy of amplification factors; small time steps
Observations
The famous diffusion equation, also known as the heat equation, reads $$ \frac{\partial u}{\partial t} = \dfc \frac{\partial^2 u}{\partial x^2} $$
Here,
Note:
Mesh in time: $$ \begin{equation} 0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T \label{_auto1} \end{equation} $$
Mesh in space: $$ \begin{equation} 0 = x_0 < x_1 < x_2 < \cdots < x_{N_x-1} < x_{N_x} = L \label{_auto2} \end{equation} $$
Uniform mesh with constant mesh spacings \( \Delta t \) and \( \Delta x \): $$ \begin{equation} x_i = i\Delta x,\ i=0,\ldots,N_x,\quad t_i = n\Delta t,\ n=0,\ldots,N_t \label{_auto3} \end{equation} $$

Require the PDE \eqref{diffu:pde1} to be fulfilled at an arbitrary interior mesh point \( (x_i,t_n) \) leads to $$ \begin{equation} \frac{\partial}{\partial t} u(x_i, t_n) = \dfc\frac{\partial^2}{\partial x^2} u(x_i, t_n) \label{diffu:pde1:step2} \end{equation} $$
Applies to all interior mesh points: \( i=1,\ldots,N_x-1 \) and \( n=1,\ldots,N_t-1 \)
For \( n=0 \) we have the initial conditions \( u=I(x) \) and \( u_t=0 \)
At the boundaries \( i=0,N_x \) we have the boundary condition \( u=0 \).
Use a forward difference in time and a centered difference in space (Forward Euler scheme): $$ \begin{equation} [D_t^+ u = \dfc D_xD_x u]^n_i \label{diffu:pde1:step3a} \end{equation} $$
Written out, $$ \begin{equation} \frac{u^{n+1}_i-u^n_i}{\Delta t} = \dfc \frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2} \label{diffu:pde1:step3b} \end{equation} $$
Initial condition: \( u^0_i = I(x_i) \), \( i=0,1,\ldots,N_x \).
where $$ F = \dfc\frac{\Delta t}{\Delta x^2} $$
There is only one parameter, \( F \), in the discrete model: \( F \) lumps mesh parameters \( \Delta t \) and \( \Delta x \) with the only physical parameter, the diffusion coefficient \( \dfc \). The value \( F \) and the smoothness of \( I(x) \) govern the quality of the numerical solution.

We visit one mesh point \( (x_i,t_{n+1}) \) at a time, and we have an explicit formula for computing the associated \( u^{n+1}_i \) value. The spatial points can be updated in any sequence, but the time levels \( t_n \) must be updated in cronological order: \( t_n \) before \( t_{n+1} \).
x = linspace(0, L, Nx+1) # mesh points in space
dx = x[1] - x[0]
t = linspace(0, T, Nt+1) # mesh points in time
dt = t[1] - t[0]
F = a*dt/dx**2
u = zeros(Nx+1)
u_1 = zeros(Nx+1)
# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
u_1[i] = I(x[i])
for n in range(0, Nt):
# Compute u at inner mesh points
for i in range(1, Nx):
u[i] = u_1[i] + F*(u_1[i-1] - 2*u_1[i] + u_1[i+1])
# Insert boundary conditions
u[0] = 0; u[Nx] = 0
# Update u_1 before next step
u_1[:]= u
# or more efficient switch of references
#u_1, u = u, u_1
web page or a movie file.
tmp_frame%04d.png filestmp_frame0000.png, tmp_frame0001.png, ...
Terminal> name=tmp_frame%04d.png
Terminal> fps=8 # frames per second in movie
Terminal> avconv -r $fps -i $name -vcodec flv movie.flv
Terminal> avconv -r $fps -i $name -vcodec libx64 movie.mp4
Terminal> avconv -r $fps -i $name -vcodec libvpx movie.webm
Terminal> avconv -r $fps -i $name -vcodec libtheora movie.ogg
\( N_x=50 \). The method results in a growing, unstable solution if \( F>0.5 \).
Choosing \( F=0.5 \) gives a strange saw tooth-like curve.
Lowering \( F \) to 0.25 gives a smooth (expected) solution.
\( N_x=50 \). \( F=0.5 \).
Backward difference in time, centered difference in space: $$ \begin{equation} [D_t^- u = D_xD_x u]^n_i \label{diffu:pde1:step3aBE} \end{equation} $$
Written out: $$ \begin{equation} \frac{u^{n}_i-u^{n-1}_i}{\Delta t} = \dfc\frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2} \label{diffu:pde1:step3bBE} \end{equation} $$
Assumption: \( u^{n-1}_i \) is computed, but all quantities at the new time level \( t_n \) are unknown.
We cannot solve wrt \( u^n_i \) because that unknown value is coupled to two other unknown values: \( u^n_{i-1} \) and \( u^n_{i+1} \). That is, all the new unknown values are coupled to each other in a linear system of algebraic equations.
Equation \eqref{diffu:pde1:step3bBE} written for \( i=1,\ldots,Nx-1= 1,2 \) becomes $$ \begin{align} \frac{u^{n}_1-u^{n-1}_1}{\Delta t} &= \dfc\frac{u^{n}_{2} - 2u^n_1 + u^n_{0}}{\Delta x^2} \label{_auto4}\\ \frac{u^{n}_2-u^{n-1}_2}{\Delta t} &= \dfc\frac{u^{n}_{3} - 2u^n_2 + u^n_{1}}{\Delta x^2} \label{_auto5} \end{align} $$
(The boundary values \( u^n_0 \) and \( u^n_3 \) are known as zero.)
Collecting the unknown new values on the left-hand side and writing as \( 2\times 2 \) matrix system: $$ \left(\begin{array}{cc} 1+ 2F & - F\\ - F & 1+ 2F \end{array}\right) \left(\begin{array}{c} u^{n}_1\\ u^{n}_{2}\\ \end{array}\right) = \left(\begin{array}{c} u^{n-1}_1\\ u^{n-1}_2 \end{array}\right) $$
Discretization methods that lead linear systems are known as implicit methods.
Discretization methods that avoid linear systems and have an explicit formula for each new value of the unknown are called explicit methods.
What are the unknowns in the linear system?
The nonzero elements are given by $$ \begin{align} A_{i,i-1} &= -F_o \label{_auto6}\\ A_{i,i} &= 1+ 2F_o \label{_auto7}\\ A_{i,i+1} &= -F_o \label{_auto8} \end{align} $$
for \( i=1,\ldots,N_x-1 \).
The equations for the boundary points correspond to $$ A_{0,0} = 1,\quad A_{0,1} = 0,\quad A_{N_x,N_x-1} = 0,\quad A_{N_x,N_x} = 1 $$
with $$ \begin{align} b_0 &= 0 \label{_auto10}\\ b_i &= u^{n-1}_i,\quad i=1,\ldots,N_x-1 \label{_auto11}\\ b_{N_x} &= 0 \label{_auto12} \end{align} $$
x = linspace(0, L, Nx+1) # mesh points in space
dx = x[1] - x[0]
t = linspace(0, T, N+1) # mesh points in time
u = zeros(Nx+1)
u_1 = zeros(Nx+1)
# Data structures for the linear system
A = zeros((Nx+1, Nx+1))
b = zeros(Nx+1)
for i in range(1, Nx):
A[i,i-1] = -F
A[i,i+1] = -F
A[i,i] = 1 + 2*F
A[0,0] = A[Nx,Nx] = 1
# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
u_1[i] = I(x[i])
import scipy.linalg
for n in range(0, Nt):
# Compute b and solve linear system
for i in range(1, Nx):
b[i] = -u_1[i]
b[0] = b[Nx] = 0
u[:] = scipy.linalg.solve(A, b)
# Update u_1 before next step
u_1, u = u, u_1
scipy.sparse enables storage and calculations with the three
nonzero diagonals only
# Representation of sparse matrix and right-hand side
diagonal = zeros(Nx+1)
lower = zeros(Nx)
upper = zeros(Nx)
b = zeros(Nx+1)
# Precompute sparse matrix
diagonal[:] = 1 + 2*F
lower[:] = -F #1
upper[:] = -F #1
# Insert boundary conditions
diagonal[0] = 1
upper[0] = 0
diagonal[Nx] = 1
lower[-1] = 0
import scipy.sparse
A = scipy.sparse.diags(
diagonals=[main, lower, upper],
offsets=[0, -1, 1], shape=(Nx+1, Nx+1),
format='csr')
# Set initial condition
for i in range(0,Nx+1):
u_1[i] = I(x[i])
for n in range(0, Nt):
b = u_1
b[0] = b[-1] = 0.0 # boundary conditions
u[:] = scipy.sparse.linalg.spsolve(A, b)
# Switch variables before next step
u_1, u = u, u_1
\( N_x=50 \). \( F=0.5 \).
\( N_x=50 \).
\( F=0.5 \).
\( F=5 \).
The PDE is sampled at points \( (x_i,t_{n+\half}) \) (at the spatial mesh points, but in between two temporal mesh points). $$ \frac{\partial}{\partial t} u(x_i, t_{n+\half}) = \dfc\frac{\partial^2}{\partial x^2}u(x_i, t_{n+\half}) $$ for \( i=1,\ldots,N_x-1 \) and \( n=0,\ldots, N_t-1 \).
Centered differences in space and time: $$ [D_t u = \dfc D_xD_x u]^{n+\half}_i$$
Right-hand side term: $$ \frac{1}{\Delta x^2}\left(u^{n+\half}_{i-1} - 2u^{n+\half}_i + u^{n+\half}_{i+1}\right)$$
Problem: \( u^{n+\half}_i \) is not one of the unknowns we compute.
Solution: replace \( u^{n+\half}_i \) by an arithmetic average: $$ u^{n+\half}_i\approx \half\left(u^{n}_i +u^{n+1}_{i}\right) $$
In compact notation (arithmetic average in time \( \overline{u}^t \)): $$ [D_t u = \dfc D_xD_x \overline{u}^t]^{n+\half}_i$$
Observe:
for internal points. For boundary points, $$ \begin{align} A_{0,0} &= 1 \label{_auto17}\\ A_{0,1} &= 0 \label{_auto18}\\ A_{N_x,N_x-1} &= 0 \label{_auto19}\\ A_{N_x,N_x} &= 1 \label{_auto20} \end{align} $$
Right-hand side: $$ \begin{align} b_0 &= 0 \label{_auto21}\\ b_i &= u^{n-1}_i,\quad i=1,\ldots,N_x-1 \label{_auto22}\\ b_{N_x} &= 0 \label{_auto23} \end{align} $$
Crank-Nicolson never blows up, so any \( F \) can be used (modulo loss of accuracy).
\( N_x=50 \). \( F=5 \) gives instabilities.
\( N_x=50 \). \( F=0.5 \) gives a smooth solution.
\( N_x=50 \).
\( F=0.5 \).
\( F=5 \).
The \( \theta \) rule condenses a family of finite difference approximations in time to one formula
Matrix entries: $$ A_{i,i-1} = -F_o\theta,\quad A_{i,i} = 1+2F_o\theta\quad, A_{i,i+1} = -F_o\theta$$
Right-hand side: $$ b_i = u^n_{i} + F_o(1-\theta) \frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2} $$
Laplace equation: $$ \nabla^2 u = 0,\quad \mbox{1D: } u''(x)=0$$
Poisson equation: $$ -\nabla^2 u = f,\quad \mbox{1D: } -u''(x)=f(x)$$
These are limiting behavior of time-dependent diffusion equations if $$ \lim_{t\rightarrow\infty}\frac{\partial u}{\partial t} = 0$$
Then \( u_t = \dfc u_{xx} + 0 \) in the limit \( t\rightarrow\infty \) reduces to $$ u_{xx} + f = 0$$
Looking at the numerical schemes, \( F\rightarrow\infty \) leads to the Laplace or Poisson equations (without \( f \) or with \( f \), resp.).
Good news: choose \( F \) large in the BE or CN schemes and one time step is enough to produce the stationary solution for \( t\rightarrow\infty \).
These extensions are performed exactly as for a wave equation as they only affect the spatial derivatives (which are the same as in the wave equation).
The PDE $$ u_t = \dfc u_{xx} $$ admits solutions $$ u(x,t) = Qe^{-\dfc k^2 t}\sin\left( kx\right) $$
Observations from this solution:
Test problem: $$ \begin{align*} u_t &= u_{xx},\quad &x\in (0,1),\ t\in (0,T]\\ u(0,t) &= u(1,t) = 0,\quad &t\in (0,T]\\ u(x,0) & = \sin (\pi x) + 0.1\sin(100\pi x) \end{align*} $$
Exact solution: $$ u(x,t) = e^{-\pi^2 t}\sin (\pi x) + 0.1e^{-\pi^2 10^4 t}\sin (100\pi x) $$
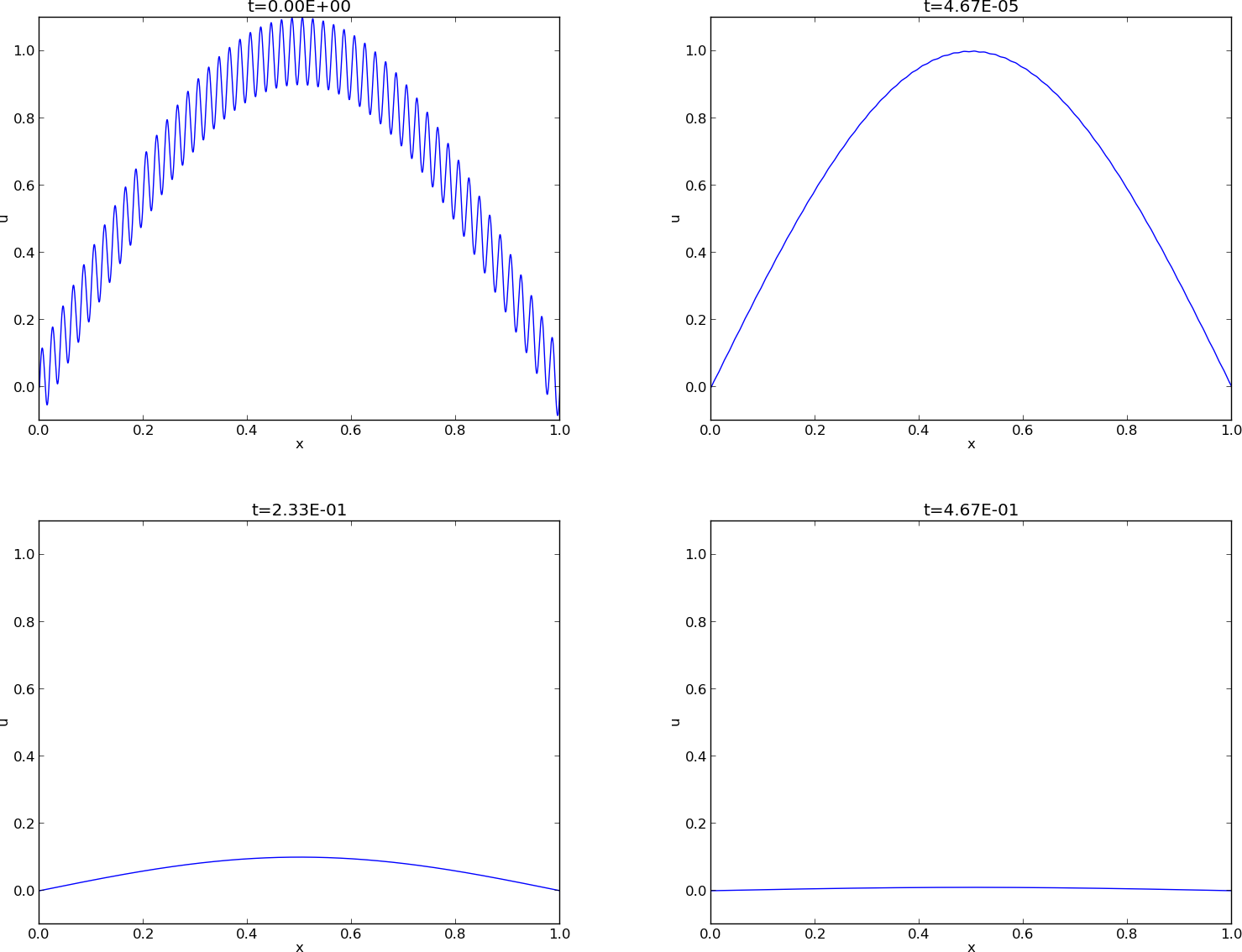
Two pieces of a material, at different temperatures, are brought in contact at \( t=0 \). Assume the end points of the pieces are kept at the initial temperature. How does the heat flow from the hot to the cold piece?
Or: A huge ion concentration on one side of a synapse in the brain (concentration discontinuity) is released and ions move by diffusion.
Assume a 1D model is sufficient (e.g., insulated rod): $$ u(x,0)=\left\lbrace \begin{array}{ll} U_L, & x < L/2\\ U_R,& x\geq L/2 \end{array}\right. $$ $$ \frac{\partial u}{\partial t} = \dfc \frac{\partial^2 u}{\partial x^2},\quad u(0,t)=U_L,\ u(L,t)=U_R$$
Discrete model: $$ [D_t^- u = \dfc D_xD_x]^n_i $$
results in a (tridiagonal) linear system $$ - F u^n_{i-1} + \left(1+ 2F \right) u^{n}_i - F u^n_{i+1} = u_{i-1}^{n-1} $$
where $$ F = \dfc\frac{\Delta t}{\Delta x^2} $$
is the mesh Fourier number
Discrete model: $$ [D_t^+ u = \dfc D_xD_x]^n_i $$
results in the explicit updating formula $$ u^{n+1}_i = u^n_i + F\left( u^{n}_{i+1} - 2u^n_i + u^n_{i-1}\right) $$
Discrete model: $$ [D_t u = \dfc D_xD_x\overline{u}^t]^n_i $$
results in a tridiagonal linear system
Represent \( I(x) \) as a Fourier series $$ I(x) \approx \sum_{k\in K} b_k e^{ikx} $$
The corresponding sum for \( u \) is $$ u(x,t) \approx \sum_{k\in K} b_k e^{-\dfc k^2t}e^{ikx} $$
Such solutions are also accepted by the numerical schemes, but with an amplification factor \( A \) different from \( \exp{({-\dfc k^2t})} \): $$ u^n_q = A^n e^{ikq\Delta x} = A^ne^{ikx} $$
Stability:
Inserting $$ u^n_q = A^n e^{ikq\Delta x}$$ leads to $$ A = 1 -4F\sin^2\left( \frac{k\Delta x}{2}\right),\quad F = \frac{\dfc\Delta t}{\Delta x^2}\mbox{ (mesh Fourier number)} $$
The complete numerical solution is $$ u^n_q = (1 -4F\sin^2 p)^ne^{ikq\Delta x},\quad p = k\Delta x/2 $$
Key spatial discretization quantity: the dimensionless \( p=\half k\Delta x \)
We always have \( A\leq 1 \). The condition \( A\geq -1 \) implies $$ 4F\sin^2p\leq 2 $$ The worst case is when \( \sin^2 p=1 \), so a sufficient criterion for stability is $$ F\leq {\half} $$ or: $$ \Delta t\leq \frac{\Delta x^2}{2\dfc} $$
Less favorable criterion than for \( u_{tt}=c^2u_{xx} \): halving \( \Delta x \) implies time step \( \frac{1}{4}\Delta t \) (not just \( \half\Delta t \) as in a wave equation). Need very small time steps for fine spatial meshes!
Stability: We see that \( |A| < 1 \) for all \( \Delta t>0 \) and that \( A>0 \) (no oscillations)
The scheme $$ [D_t u = \dfc D_xD_x \overline{u}^x]^{n+\half}_q$$ leads to $$ A = \frac{ 1 - 2F\sin^2p}{1 + 2F\sin^2p} $$ $$ u^n_q = \left(\frac{ 1 - 2F\sin^2p}{1 + 2F\sin^2p}\right)^ne^{ikp\Delta x}$$
Stability: The criteria \( A>-1 \) and \( A < 1 \) are fulfilled for any \( \Delta t >0 \)
Note: \( \Aex = \exp{(-\dfc k^2\Delta t)}=\exp{(-F k^2\Delta x^2)}= \exp{(-F4p^2)} \).