Model extensions

It is time to consider generalizations of the simple decay model \(u=-au\) and also to look at additional numerical solution methods.

Generalization: including a variable coefficient

In the ODE for decay, \(u^{\prime}=-au\), we now consider the case where \(a\) depends on time:

(1)\[ u^{\prime}(t) = -a(t)u(t),\quad t\in (0,T],\quad u(0)=I {\thinspace .}\]

A Forward Euler scheme consist of evaluating (1) at \(t=t_n\) and approximating the derivative with a forward difference \([D^+_t u]^n\):

\[\frac{u^{n+1} - u^n}{\Delta t} = -a(t_n)u^n {\thinspace .}\]

The Backward Euler scheme becomes

\[\frac{u^{n} - u^{n-1}}{\Delta t} = -a(t_n)u^n {\thinspace .}\]

The Crank-Nicolson method builds on sampling the ODE at \(t_{n+\frac{1}{2}}\). We can evaluate \(a\) at \(t_{n+\frac{1}{2}}\) and use an average for \(u\) at times \(t_n\) and \(t_{n+1}\):

\[\frac{u^{n+1} - u^{n}}{\Delta t} = -a(t_{n+\frac{1}{2}})\frac{1}{2}(u^n + u^{n+1}) {\thinspace .}\]

Alternatively, we can use an average for the product \(au\):

\[\frac{u^{n+1} - u^{n}}{\Delta t} = -\frac{1}{2}(a(t_n)u^n + a(t_{n+1})u^{n+1}) {\thinspace .}\]

The \(\theta\)-rule unifies the three mentioned schemes. One version is to have \(a\) evaluated at the weighted time point \((1-\theta)t_n + \theta t_{n+1}\),

\[\frac{u^{n+1} - u^{n}}{\Delta t} = -a((1-\theta)t_n + \theta t_{n+1})((1-\theta) u^n + \theta u^{n+1}) {\thinspace .}\]

Another possibility is to apply a weighted average for the product \(au\),

\[\frac{u^{n+1} - u^{n}}{\Delta t} = -(1-\theta) a(t_n)u^n - \theta a(t_{n+1})u^{n+1} {\thinspace .}\]

With the finite difference operator notation the Forward Euler and Backward Euler schemes can be summarized as

\[\lbrack D^+_t u = -au\rbrack^n,\]

\[\lbrack D^-_t u = -au\rbrack^n {\thinspace .}\]

The Crank-Nicolson and \(\theta\) schemes depend on whether we evaluate \(a\) at the sample point for the ODE or if we use an average. The various versions are written as

\[\lbrack D_t u = -a\overline{u}^t\rbrack^{n+\frac{1}{2}},\]

\[\lbrack D_t u = -\overline{au}^t\rbrack^{n+\frac{1}{2}},\]

\[\lbrack D_t u = -a\overline{u}^{t,\theta}\rbrack^{n+\theta},\]

\[\lbrack D_t u = -\overline{au}^{t,\theta}\rbrack^{n+\theta} {\thinspace .}\]

Generalization: including a source term

A further extension of the model ODE is to include a source term \(b(t)\):

(2)\[ u^{\prime}(t) = -a(t)u(t) + b(t),\quad t\in (0,T],\quad u(0)=I {\thinspace .}\]

The time point where we sample the ODE determines where \(b(t)\) is evaluated. For the Crank-Nicolson scheme and the \(\theta\)-rule we have a choice of whether to evaluate \(a(t)\) and \(b(t)\) at the correct point or use an average. The chosen strategy becomes particularly clear if we write up the schemes in the operator notation:

\[\lbrack D^+_t u = -au + b\rbrack^n,\]

\[\lbrack D^-_t u = -au + b\rbrack^n,\]

\[\lbrack D_t u = -a\overline{u}^t + b\rbrack^{n+\frac{1}{2}},\]

\[\lbrack D_t u = \overline{-au+b}^t\rbrack^{n+\frac{1}{2}},\]

\[\lbrack D_t u = -a\overline{u}^{t,\theta} + b\rbrack^{n+\theta},\]

(3)\[ \lbrack D_t u = \overline{-au+b}^{t,\theta}\rbrack^{n+\theta}\]\[ {\thinspace .}\]

Implementation of the generalized model problem

Deriving the \(\theta\)-rule formula

Writing out the \(\theta\)-rule in (3), using (2.37) and (2.38), we get

(4)\[ \frac{u^{n+1}-u^n}{\Delta t} = \theta(-a^{n+1}u^{n+1} + b^{n+1})) + (1-\theta)(-a^nu^{n} + b^n)),\]

where \(a^n\) means evaluating \(a\) at \(t=t_n\) and similar for \(a^{n+1}\), \(b^n\), and \(b^{n+1}\). We solve for \(u^{n+1}\):

\[u^{n+1} = ((1 - \Delta t(1-\theta)a^n)u^n + \Delta t(\theta b^{n+1} + (1-\theta)b^n))(1 + \Delta t\theta a^{n+1})^{-1} {\thinspace .}\]

Python code

Here is a suitable implementation of (4) where \(a(t)\) and \(b(t)\) are given as Python functions:

def solver(I, a, b, T, dt, theta):
    """
    Solve u'=-a(t)*u + b(t), u(0)=I,
    for t in (0,T] with steps of dt.
    a and b are Python functions of t.
    """
    dt = float(dt)            # avoid integer division
    Nt = int(round(T/dt))     # no of time intervals
    T = Nt*dt                 # adjust T to fit time step dt
    u = zeros(Nt+1)           # array of u[n] values
    t = linspace(0, T, Nt+1)  # time mesh

    u[0] = I                  # assign initial condition
    for n in range(0, Nt):    # n=0,1,...,Nt-1
        u[n+1] = ((1 - dt*(1-theta)*a(t[n]))*u[n] + \
                  dt*(theta*b(t[n+1]) + (1-theta)*b(t[n])))/\
                  (1 + dt*theta*a(t[n+1]))
    return u, t

This function is found in the file decay_vc.py (vc stands for “variable coefficients”).

Coding of variable coefficients

The solver function shown above demands the arguments a and b to be Python functions of time t, say

def a(t):
    return a_0 if t < tp else k*a_0

def b(t):
    return 1

Here, a(t) has three parameters a0, tp, and k, which must be global variables.

A better implementation, which avoids global variables, is to represent a by a class where the parameters are attributes and where a special method __call__ evaluates \(a(t)\):

class A:
    def __init__(self, a0=1, k=2):
        self.a0, self.k = a0, k

    def __call__(self, t):
        return self.a0 if t < self.tp else self.k*self.a0

a = A(a0=2, k=1)  # a behaves as a function a(t)

For quick tests it is cumbersome to write a complete function or a class. The lambda function construction in Python is then convenient. For example,

a = lambda t: a_0 if t < tp else k*a_0

is equivalent to the def a(t) definition above. In general,

f = lambda arg1, arg2, ...: expression

is equivalent to

def f(arg1, arg2, ...):
    return expression

One can use lambda functions directly in calls. Say we want to solve \(u^{\prime}=-u+1\), \(u(0)=2\):

u, t = solver(2, lambda t: 1, lambda t: 1, T, dt, theta)

Whether to use a plain function, a class, or a lambda function depends on the programmer’s taste. Lazy programmers prefer the lambda construct, while very safe programmers go for the class solution.

Verifying a constant solution

An extremely useful partial verification method is to construct a test problem with a very simple solution, usually \(u=\hbox{const}\). Especially the initial debugging of a program code can benefit greatly from such tests, because 1) all relevant numerical methods will exactly reproduce a constant solution, 2) many of the intermediate calculations are easy to control by hand for a constant \(u\), and 3) even a constant \(u\) can uncover many bugs in an implementation.

The only constant solution for the problem \(u^{\prime}=-au\) is \(u=0\), but too many bugs can escape from that trivial solution. It is much better to search for a problem where \(u=C=\hbox{const}\neq 0\). Then \(u^{\prime}=-a(t)u + b(t)\) is more appropriate: with \(u=C\) we can choose any \(a(t)\) and set \(b=a(t)C\) and \(I=C\). An appropriate test function is

def test_constant_solution():
    """
    Test problem where u=u_const is the exact solution, to be
    reproduced (to machine precision) by any relevant method.
    """
    def exact_solution(t):
        return u_const

    def a(t):
        return 2.5*(1+t**3)  # can be arbitrary

    def b(t):
        return a(t)*u_const

    u_const = 2.15
    theta = 0.4; I = u_const; dt = 4
    Nt = 4  # enough with a few steps
    u, t = solver(I=I, a=a, b=b, T=Nt*dt, dt=dt, theta=theta)
    print u
    u_e = exact_solution(t)
    difference = abs(u_e - u).max()  # max deviation
    tol = 1E-14
    assert difference < tol

An interesting question is what type of bugs that will make the computed \(u^n\) deviate from the exact solution \(C\). Fortunately, the updating formula and the initial condition must be absolutely correct for the test to pass! Any attempt to make a wrong indexing in terms like a(t[n]) or any attempt to introduce an erroneous factor in the formula creates a solution that is different from \(C\).

Verification via manufactured solutions

Following the idea of the previous section, we can choose any formula as the exact solution, insert the formula in the ODE problem and fit the data \(a(t)\), \(b(t)\), and \(I\) to make the chosen formula fulfill the equation. This powerful technique for generating exact solutions is very useful for verification purposes and known as the method of manufactured solutions, often abbreviated MMS.

One common choice of solution is a linear function in the independent variable(s). The rationale behind such a simple variation is that almost any relevant numerical solution method for differential equation problems is able to reproduce a linear function exactly to machine precision (if \(u\) is about unity in size; precision is lost if \(u\) takes on large values, see Exercise 9: Experiment with precision in tests and the size of ). The linear solution also makes some stronger demands to the numerical method and the implementation than the constant solution used in the section Verifying a constant solution, at least in more complicated applications. Still, the constant solution is often ideal for initial debugging before proceeding with a linear solution.

We choose a linear solution \(u(t) = ct + d\). From the initial condition it follows that \(d=I\). Inserting this \(u\) in the left-hand side of (2), i.e., the ODE, we get

\[c = -a(t)u + b(t) {\thinspace .}\]

Any function \(u=ct+I\) is then a correct solution if we choose

\[b(t) = c + a(t)(ct + I) {\thinspace .}\]

With this \(b(t)\) there are no restrictions on \(a(t)\) and \(c\).

Let us prove that such a linear solution obeys the numerical schemes. To this end, we must check that \(u^n = ca(t_n)(ct_n+I)\) fulfills the discrete equations. For these calculations, and later calculations involving linear solutions inserted in finite difference schemes, it is convenient to compute the action of a difference operator on a linear function \(t\):

(5)\[ \lbrack D_t^+ t\rbrack^n = \frac{t_{n+1}-t_n}{\Delta t}=1,\]

(6)\[ \lbrack D_t^- t\rbrack^n = \frac{t_{n}-t_{n-1}}{\Delta t}=1,\]

(7)\[ \lbrack D_t t\rbrack^n = \frac{t_{n+\frac{1}{2}}-t_{n-\frac{1}{2}}}{\Delta t}=\frac{(n+\frac{1}{2})\Delta t - (n-\frac{1}{2})\Delta t}{\Delta t}=1\]\[ {\thinspace .}\]

Clearly, all three finite difference approximations to the derivative are exact for \(u(t)=t\) or its mesh function counterpart \(u^n = t_n\).

The difference equation for the Forward Euler scheme

\[[D^+_t u = -au + b]^n,\]

with \(a^n=a(t_n)\), \(b^n=c + a(t_n)(ct_n + I)\), and \(u^n=ct_n + I\) then results in

\[c = -a(t_n)(ct_n+I) + c + a(t_n)(ct_n + I) = c\]

which is always fulfilled. Similar calculations can be done for the Backward Euler and Crank-Nicolson schemes, or the \(\theta\)-rule for that matter. In all cases, \(u^n=ct_n +I\) is an exact solution of the discrete equations. That is why we should expect that \(u^n - {u_{\small\mbox{e}}}(t_n) =0\) mathematically and \(|u^n - {u_{\small\mbox{e}}}(t_n)|\) less than a small number about the machine precision for \(n=0,\ldots,N_t\).

The following function offers an implementation of this verification test based on a linear exact solution:

def test_linear_solution():
    """
    Test problem where u=c*t+I is the exact solution, to be
    reproduced (to machine precision) by any relevant method.
    """
    def exact_solution(t):
        return c*t + I

    def a(t):
        return t**0.5  # can be arbitrary

    def b(t):
        return c + a(t)*exact_solution(t)

    theta = 0.4; I = 0.1; dt = 0.1; c = -0.5
    T = 4
    Nt = int(T/dt)  # no of steps
    u, t = solver(I=I, a=a, b=b, T=Nt*dt, dt=dt, theta=theta)
    u_e = exact_solution(t)
    difference = abs(u_e - u).max()  # max deviation
    print difference
    tol = 1E-14  # depends on c!
    assert difference < tol

Any error in the updating formula makes this test fail!

Choosing more complicated formulas as the exact solution, say \(\cos(t)\), will not make the numerical and exact solution coincide to machine precision, because finite differencing of \(\cos(t)\) does not exactly yield the exact derivative \(-\sin(t)\). In such cases, the verification procedure must be based on measuring the convergence rates as exemplified in the section Computing convergence rates. Convergence rates can be computed as long as one has an exact solution of a problem that the solver can be tested on, but this can always be obtained by the method of manufactured solutions.

Computing convergence rates

We expect that the error \(E\) in the numerical solution is reduced if the mesh size \(\Delta t\) is decreased. More specifically, many numerical methods obey a power-law relation between \(E\) and \(\Delta t\):

(8)\[ E = C\Delta t^r,\]

where \(C\) and \(r\) are (usually unknown) constants independent of \(\Delta t\). The formula (8) is viewed as an asymptotic model valid for sufficiently small \(\Delta t\). How small is normally hard to estimate without doing numerical estimations of \(r\).

The parameter \(r\) is known as the convergence rate. For example, if the convergence rate is 2, halving \(\Delta t\) reduces the error by a factor of 4. Diminishing \(\Delta t\) then has a greater impact on the error compared with methods that have \(r=1\). For a given value of \(r\), we refer to the method as of \(r\)-th order. First- and second-order methods are most common in scientific computing.

Estimating \(r\)

There are two alternative ways of estimating \(C\) and \(r\) based on a set of \(m\) simulations with corresponding pairs \((\Delta t_i, E_i)\), \(i=0,\ldots,m-1\), and \(\Delta t_{i} < \Delta t_{i-1}\) (i.e., decreasing cell size).

1. Take the logarithm of (8), \(\ln E = r\ln \Delta t + \ln C\), and fit a straight line to the data points \((\Delta t_i, E_i)\), \(i=0,\ldots,m-1\).
2. Consider two consecutive experiments, \((\Delta t_i, E_i)\) and \((\Delta t_{i-1}, E_{i-1})\). Dividing the equation \(E_{i-1}=C\Delta t_{i-1}^r\) by \(E_{i}=C\Delta t_{i}^r\) and solving for \(r\) yields

(9)\[ r_{i-1} = \frac{\ln (E_{i-1}/E_i)}{\ln (\Delta t_{i-1}/\Delta t_i)}\]

for \(i=1,\ldots,m-1\). Note that we have introduced a subindex \(i-1\) on \(r\) in (9) because \(r\) estimated from a pair of experiments must be expected to change with \(i\).

The disadvantage of method 1 is that (8) might not be valid for the coarsest meshes (largest \(\Delta t\) values). Fitting a line to all the data points is then misleading. Method 2 computes convergence rates for pairs of experiments and allows us to see if the sequence \(r_i\) converges to some value as \(i\rightarrow m-2\). The final \(r_{m-2}\) can then be taken as the convergence rate. If the coarsest meshes have a differing rate, the corresponding time steps are probably too large for (8) to be valid. That is, those time steps lie outside the asymptotic range of \(\Delta t\) values where the error behaves like (8).

Implementation (2)

Suppose we have some function error(dt, ...) that can compute the numerical error in our mathematical model. To compute \(r_0, r_1, \ldots, r_{m-2}\) from (8), we just wrap a loop over \(\Delta t\) values (dt_values) around the error function:

E_values = [error(dt, ...) for dt in dt_values]

# Compute pairwise convergence rates
m = len(dt_values)
r = [log(E_values[i-1]/E_values[i])/
     log(dt_values[i-1]/dt_values[i])
     for i in range(1, m, 1)]

# Strip off to 2 decimals
r = [round(r_, 2) for r_ in r]

We can run the convergence rate estimate computations for the \(\theta\)-rule discretization of \(u'=-au\), using \(\Delta t = 0.5,-.25, 0.1, 0.05, 0.025, 0.01\):

FE: 1.33 1.15 1.07 1.03 1.02
BE: 0.98 0.99 0.99 1.00 1.00
CN: 2.14 2.07 2.03 2.01 2.01

The Forward and Backward Euler methods seem to have an \(r\) value which stabilizes at 1, while the Crank-Nicolson seems to be a second-order method with \(r=2\). These results are in very good agreement with various theoretical considerations for \(r\).

Why convergence rates are important

The strong practical application of computing convergence rates is for verification: wrong convergence rates point to errors in the code, and correct convergence rates bring strong support for a correct implementation. Experience shows that bugs in the code easily destroy the expected convergence rate.

Extension to systems of ODEs

Many ODE models involve more than one unknown function and more than one equation. Here is an example of two unknown functions \(u(t)\) and \(v(t)\):

\[u^{\prime} = a u + bv,\]

\[v^{\prime} = cu + dv,\]

for constants \(a,b,c,d\). Applying the Forward Euler method to each equation results in a simple updating formula:

\[u^{n+1} = u^n + \Delta t (a u^n + b v^n),\]

\[v^{n+1} = u^n + \Delta t (cu^n + dv^n) {\thinspace .}\]

On the other hand, the Crank-Nicolson or Backward Euler schemes result in a \(2\times 2\) linear system for the new unknowns. The latter scheme becomes

\[u^{n+1} = u^n + \Delta t (a u^{n+1} + b v^{n+1}),\]

\[v^{n+1} = v^n + \Delta t (c u^{n+1} + d v^{n+1}){\thinspace .}\]

Collecting \(u^{n+1}\) as well as \(v^{n+1}\) on the left-hand side results in

\[(1 - \Delta t a)u^{n+1} + bv^{n+1} = u^n ,\]

\[c u^{n+1} + (1 - \Delta t d) v^{n+1} = v^n ,\]

which is a system of two coupled, linear, algebraic equations in two unknowns. These equations can be solved by hand (using standard techniques for two algebraic equations with two unknowns \(x\) and \(y\)), resulting in explicit formulas for \(u^{n+1}\) and \(v^{n+1}\) that can be directly implemented. For systems of ODEs with many equations and unknowns, one will express the coupled equations at each time level in matrix form and call software for numerical solution of linear systems of equations.

General first-order ODEs

We now turn the attention to general, nonlinear ODEs and systems of such ODEs. Our focus is on numerical methods that can be readily reused for time-discretization of PDEs, and diffusion PDEs in particular. The methods are just briefly listed, and we refer to the rich literature for more detailed descriptions and analysis - the books [Ref05] [Ref06] [Ref07] [Ref08] are all excellent resources on numerical methods for ODEs. We also demonstrate the Odespy Python interface to a range of different software for general first-order ODE systems.

Generic form of first-order ODEs

ODEs are commonly written in the generic form

(10)\[ u^{\prime} = f(u,t),\quad u(0)=I,\]

where \(f(u,t)\) is some prescribed function. As an example, our most general exponential decay model (2) has \(f(u,t)=-a(t)u(t) + b(t)\).

The unknown \(u\) in (10) may either be a scalar function of time \(t\), or a vector valued function of \(t\) in case of a system of ODEs with \(m\) unknown components:

\[u(t) = (u^{(0)}(t),u^{(1)}(t),\ldots,u^{(m-1)}(t)) {\thinspace .}\]

In that case, the right-hand side is vector-valued function with \(m\) components,

\[\begin{split}f(u, t) = ( & f^{(0)}(u^{(0)}(t),\ldots,u^{(m-1)}(t)),\\ & f^{(1)}(u^{(0)}(t),\ldots,u^{(m-1)}(t)),\\ & \vdots,\\ & f^{(m-1)}(u^{(0)}(t),\ldots,u^{(m-1)}(t))) {\thinspace .}\end{split}\]

Actually, any system of ODEs can be written in the form (10), but higher-order ODEs then need auxiliary unknown functions to enable conversion to a first-order system.

Next we list some well-known methods for \(u^{\prime}=f(u,t)\), valid both for a single ODE (scalar \(u\)) and systems of ODEs (vector \(u\)).

The \(\theta\)-rule

The \(\theta\)-rule scheme applied to \(u^{\prime}=f(u,t)\) becomes

(11)\[ \frac{u^{n+1}-u^n}{\Delta t} = \theta f(u^{n+1},t_{n+1}) + (1-\theta)f(u^n, t_n){\thinspace .}\]

Bringing the unknown \(u^{n+1}\) to the left-hand side and the known terms on the right-hand side gives

\[u^{n+1} - \Delta t \theta f(u^{n+1},t_{n+1}) = u^n + \Delta t(1-\theta)f(u^n, t_n){\thinspace .}\]

For a general \(f\) (not linear in \(u\)), this equation is nonlinear in the unknown \(u^{n+1}\) unless \(\theta = 0\). For a scalar ODE (\(m=1\)), we have to solve a single nonlinear algebraic equation for \(u^{n+1}\), while for a system of ODEs, we get a system of coupled, nonlinear algebraic equations. Newton’s method is a popular solution approach in both cases. Note that with the Forward Euler scheme (\(\theta =0\)) we do not have to deal with nonlinear equations, because in that case we have an explicit updating formula for \(u^{n+1}\). This is known as an explicit scheme. With \(\theta\neq 1\) we have to solve (systems of) algebraic equations, and the scheme is said to be implicit.

An implicit 2-step backward scheme

The implicit backward method with 2 steps applies a three-level backward difference as approximation to \(u^{\prime}(t)\),

\[u^{\prime}(t_{n+1}) \approx \frac{3u^{n+1} - 4u^{n} + u^{n-1}}{2\Delta t},\]

which is an approximation of order \(\Delta t^2\) to the first derivative. The resulting scheme for \(u^{\prime}=f(u,t)\) reads

(12)\[ u^{n+1} = \frac{4}{3}u^n - \frac{1}{3}u^{n-1} + \frac{2}{3}\Delta t f(u^{n+1}, t_{n+1}) {\thinspace .}\]

Higher-order versions of the scheme (12) can be constructed by including more time levels. These schemes are known as the Backward Differentiation Formulas (BDF), and the particular version (12) is often referred to as BDF2.

Note that the scheme (12) is implicit and requires solution of nonlinear equations when \(f\) is nonlinear in \(u\). The standard 1st-order Backward Euler method or the Crank-Nicolson scheme can be used for the first step.

Leapfrog schemes

The ordinary Leapfrog scheme

The derivative of \(u\) at some point \(t_n\) can be approximated by a central difference over two time steps,

\[u^{\prime}(t_n)\approx \frac{u^{n+1}-u^{n-1}}{2\Delta t} = [D_{2t}u]^n\]

which is an approximation of second order in \(\Delta t\). The scheme can then be written as

\[[D_{2t}u=f(u,t)]^n,\]

in operator notation. Solving for \(u^{n+1}\) gives

(13)\[ u^{n+1} = u^{n-1} + 2\Delta t f(u^n, t_n) {\thinspace .}\]

Observe that (13) is an explicit scheme, and that a nonlinear \(f\) (in \(u\)) is trivial to handle since it only involves the known \(u^n\) value. Some other scheme must be used as starter to compute \(u^1\), preferably the Forward Euler scheme since it is also explicit.

The filtered Leapfrog scheme

Unfortunately, the Leapfrog scheme (13) will develop growing oscillations with time (see Problem 14: Implement and investigate the Leapfrog scheme). A remedy for such undesired oscillations is to introduce a filtering technique. First, a standard Leapfrog step is taken, according to (13), and then the previous \(u^n\) value is adjusted according to

(14)\[ u^n\ \leftarrow\ u^n + \gamma (u^{n-1} - 2u^n + u^{n+1})\]\[ {\thinspace .}\]

The \(\gamma\)-terms will effectively damp oscillations in the solution, especially those with short wavelength (like point-to-point oscillations). A common choice of \(\gamma\) is 0.6 (a value used in the famous NCAR Climate Model).

The 2nd-order Runge-Kutta method

The two-step scheme

(15)\[ u^* = u^n + \Delta t f(u^n, t_n),\]

(16)\[ u^{n+1} = u^n + \Delta t \frac{1}{2} \left( f(u^n, t_n) + f(u^*, t_{n+1}) \right),\]

essentially applies a Crank-Nicolson method (16) to the ODE, but replaces the term \(f(u^{n+1}, t_{n+1})\) by a prediction \(f(u^{*}, t_{n+1})\) based on a Forward Euler step (15). The scheme (15)-(16) is known as Huen’s method, but is also a 2nd-order Runge-Kutta method. The scheme is explicit, and the error is expected to behave as \(\Delta t^2\).

A 2nd-order Taylor-series method

One way to compute \(u^{n+1}\) given \(u^n\) is to use a Taylor polynomial. We may write up a polynomial of 2nd degree:

\[u^{n+1} = u^n + u^{\prime}(t_n)\Delta t + {\frac{1}{2}}u^{\prime\prime}(t_n)\Delta t^2 {\thinspace .}\]

From the equation \(u^{\prime}=f(u,t)\) it follows that the derivatives of \(u\) can be expressed in terms of \(f\) and its derivatives:

\[\begin{split}u^{\prime}(t_n) &=f(u^n,t_n),\\ u^{\prime\prime}(t_n) &= \frac{\partial f}{\partial u}(u^n,t_n) u^{\prime}(t_n) + \frac{\partial f}{\partial t}\\ &= f(u^n,t_n)\frac{\partial f}{\partial u}(u^n,t_n) + \frac{\partial f}{\partial t},\end{split}\]

resulting in the scheme

(17)\[ u^{n+1} = u^n + f(u^n,t_n)\Delta t + \frac{1}{2}\left( f(u^n,t_n)\frac{\partial f}{\partial u}(u^n,t_n) + \frac{\partial f}{\partial t}\right)\Delta t^2 {\thinspace .}\]

More terms in the series could be included in the Taylor polynomial to obtain methods of higher order than 2.

The 2nd- and 3rd-order Adams-Bashforth schemes

The following method is known as the 2nd-order Adams-Bashforth scheme:

(18)\[ u^{n+1} = u^n + \frac{1}{2}\Delta t\left( 3f(u^n, t_n) - f(u^{n-1}, t_{n-1}) \right) {\thinspace .}\]

The scheme is explicit and requires another one-step scheme to compute \(u^1\) (the Forward Euler scheme or Heun’s method, for instance). As the name implies, the error behaves like \(\Delta t^2\).

Another explicit scheme, involving four time levels, is the 3rd-order Adams-Bashforth scheme

(19)\[ u^{n+1} = u^n + \frac{1}{12}\left( 23f(u^n, t_n) - 16 f(u^{n-1},t_{n-1}) + 5f(u^{n-2}, t_{n-2})\right) {\thinspace .}\]

The numerical error is of order \(\Delta t^3\), and the scheme needs some method for computing \(u^1\) and \(u^2\).

More general, higher-order Adams-Bashforth schemes (also called explicit Adams methods) compute \(u^{n+1}\) as a linear combination of \(f\) at \(k+1\) previous time steps:

\[u^{n+1} = u^n + \sum_{j=0}^k \beta_jf(u^{n-j},t_{n-j}),\]

where \(\beta_j\) are known coefficients.

The 4th-order Runge-Kutta method

The perhaps most widely used method to solve ODEs is the 4th-order Runge-Kutta method, often called RK4. Its derivation is a nice illustration of common numerical approximation strategies, so let us go through the steps in detail to learn about algorithmic development.

The starting point is to integrate the ODE \(u^{\prime}=f(u,t)\) from \(t_n\) to \(t_{n+1}\):

\[u(t_{n+1}) - u(t_n) = \int\limits_{t_{n}}^{t_{n+1}} f(u(t),t)dt{\thinspace .}\]

We want to compute \(u(t_{n+1})\) and regard \(u(t_n)\) as known. The task is to find good approximations for the integral, since the integrand involves the unknown \(u\) between \(t_n\) and \(t_{n+1}\).

The integral can be approximated by the famous Simpson’s rule:

\[\int\limits_{t_{n}}^{t_{n+1}} f(u(t),t)dt \approx \frac{\Delta t}{6}\left( f^n + 4f^{n+\frac{1}{2}} + f^{n+1}\right){\thinspace .}\]

The problem now is that we do not know \(f^{n+\frac{1}{2}}=f(u^{n+\frac{1}{2}},t_{n+\frac{1}{2}})\) and \(f^{n+1}=(u^{n+1},t_{n+1})\) as we know only \(u^n\) and hence \(f^n\). The idea is to use various approximations for \(f^{n+\frac{1}{2}}\) and \(f^{n+1}\) based on well-known schemes for the ODE in the intervals \([t_n,t_{n+\frac{1}{2}}]\) and \([t_n, t_{n+1}]\). We split the integral approximation into four terms:

\[\int\limits_{t_{n}}^{t_{n+1}} f(u(t),t)dt \approx \frac{\Delta t}{6}\left( f^n + 2\hat{f}^{n+\frac{1}{2}} + 2\tilde{f}^{n+\frac{1}{2}} + \bar{f}^{n+1}\right),\]

where \(\hat{f}^{n+\frac{1}{2}}\), \(\tilde{f}^{n+\frac{1}{2}}\), and \(\bar{f}^{n+1}\) are approximations to \(f^{n+\frac{1}{2}}\) and \(f^{n+1}\), respectively, that can be based on already computed quantities. For \(\hat{f}^{n+\frac{1}{2}}\) we can apply an approximation to \(u^{n+\frac{1}{2}}\) using the Forward Euler method with step \(\frac{1}{2}\Delta t\):

(20)\[ \hat{f}^{n+\frac{1}{2}} = f(u^n + \frac{1}{2}{\Delta t} f^n, t_{n+\frac{1}{2}})\]

Since this gives us a prediction of \(f^{n+\frac{1}{2}}\), we can for \(\tilde{f}^{n+\frac{1}{2}}\) try a Backward Euler method to approximate \(u^{n+\frac{1}{2}}\):

(21)\[ \tilde{f}^{n+\frac{1}{2}} = f(u^n + \frac{1}{2}\Delta t\hat{f}^{n+\frac{1}{2}}, t_{n+\frac{1}{2}}){\thinspace .}\]

With \(\tilde{f}^{n+\frac{1}{2}}\) as a hopefully good approximation to \(f^{n+\frac{1}{2}}\), we can for the final term \(\bar{f}^{n+1}\) use a Crank-Nicolson method to approximate \(u^{n+1}\):

(22)\[ \bar{f}^{n+1} = f(u^n + \Delta t \hat{f}^{n+\frac{1}{2}}, t_{n+1}){\thinspace .}\]

We have now used the Forward and Backward Euler methods as well as the Crank-Nicolson method in the context of Simpson’s rule. The hope is that the combination of these methods yields an overall time-stepping scheme from \(t_n\) to \(t_n{+1}\) that is much more accurate than the \({\mathcal{O}(\Delta t)}\) and \({\mathcal{O}(\Delta t^2)}\) of the individual steps. This is indeed true: the overall accuracy is \({\mathcal{O}(\Delta t^4)}\)!

To summarize, the 4th-order Runge-Kutta method becomes

\[u^{n+1} = u^n + \frac{\Delta t}{6}\left( f^n + 2\hat{f}^{n+\frac{1}{2}} + 2\tilde{f}^{n+\frac{1}{2}} + \bar{f}^{n+1}\right),\]

where the quantities on the right-hand side are computed from (20)-(22). Note that the scheme is fully explicit so there is never any need to solve linear or nonlinear algebraic equations. However, the stability is conditional and depends on \(f\). There is a whole range of implicit Runge-Kutta methods that are unconditionally stable, but require solution of algebraic equations involving \(f\) at each time step.

The simplest way to explore more sophisticated methods for ODEs is to apply one of the many high-quality software packages that exist, as the next section explains.

The Odespy software

A wide range of methods and software exist for solving (10). Many of the methods are accessible through a unified Python interface offered by the Odespy [Ref09] package. Odespy features simple Python implementations of the most fundamental schemes as well as Python interfaces to several famous packages for solving ODEs: ODEPACK, Vode, rkc.f, rkf45.f, as well as the ODE solvers in SciPy, SymPy, and odelab.

The usage of Odespy follows this setup for the ODE \(u^{\prime}=-au\), \(u(0)=I\), \(t\in (0,T]\), here solved by the famous 4th-order Runge-Kutta method with \(\Delta t=1\) and \(N_t=6\) steps:

def f(u, t):
    return -a*u

import odespy
import numpy as np

I = 1; a = 0.5; Nt = 6; dt = 1
solver = odespy.RK4(f)
solver.set_initial_condition(I)
t_mesh = np.linspace(0, Nt*dt, Nt+1)
u, t = solver.solve(t_mesh)

The previously listed methods for ODEs are all accessible in Odespy:

• the \(\theta\)-rule: ThetaRule
• special cases of the \(\theta\)-rule: ForwardEuler, BackwardEuler, CrankNicolson
• the 2nd- and 4th-order Runge-Kutta methods: RK2 and RK4
• The BDF methods and the Adam-Bashforth methods: Vode, Lsode, Lsoda, lsoda_scipy
• The Leapfrog schemes: Leapfrog and LeapfrogFiltered

Example: Runge-Kutta methods

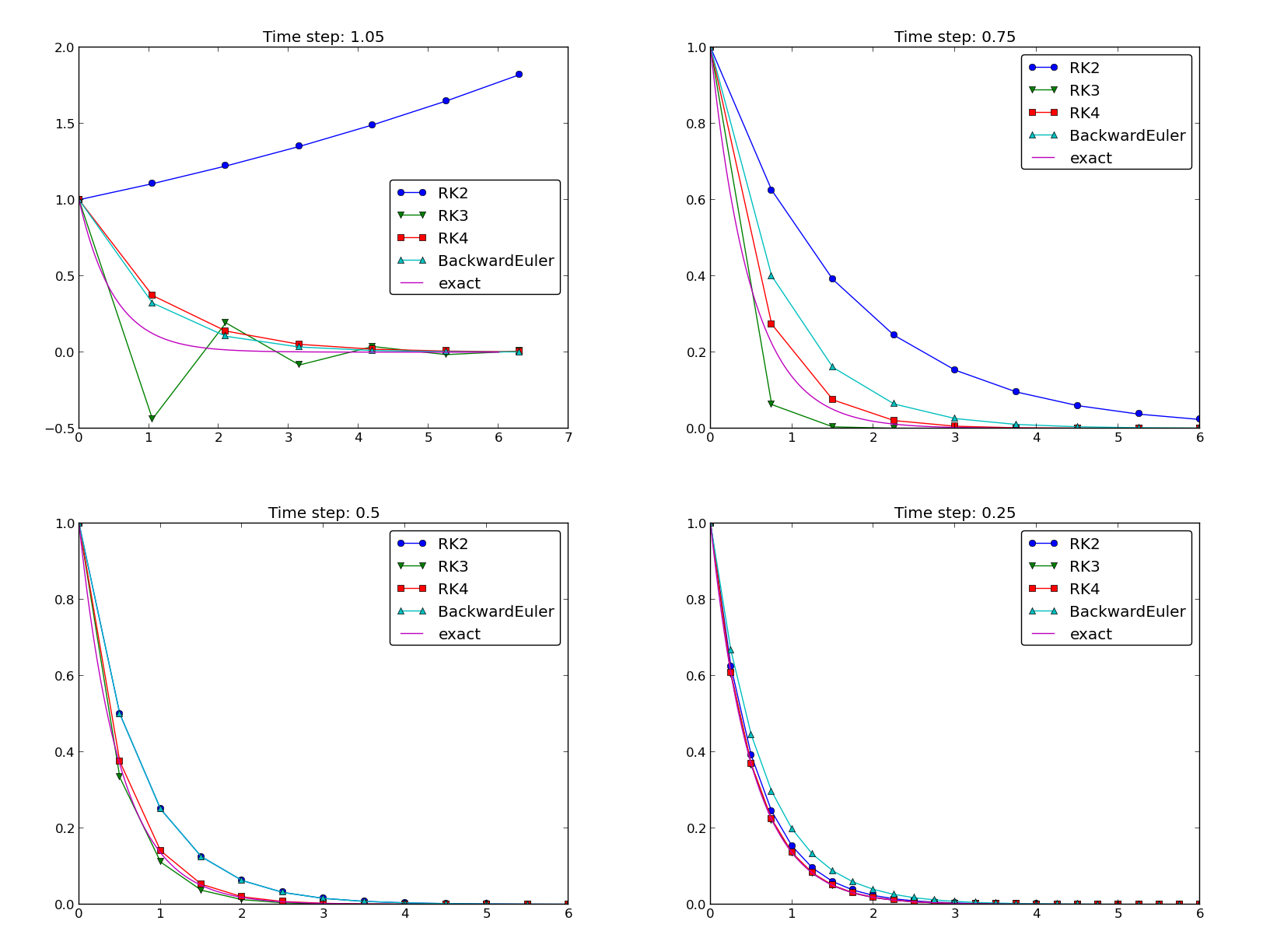
Since all solvers have the same interface in Odespy, except for a potentially different set of parameters in the solvers’ constructors, one can easily make a list of solver objects and run a loop for comparing a lot of solvers. The code below, found in complete form in decay_odespy.py, compares the famous Runge-Kutta methods of orders 2, 3, and 4 with the exact solution of the decay equation \(u^{\prime}=-au\). Since we have quite long time steps, we have included the only relevant \(\theta\)-rule for large time steps, the Backward Euler scheme (\(\theta=1\)), as well. Figure Behavior of different schemes for the decay equation shows the results.

import numpy as np
import matplotlib.pyplot as plt
import sys

def f(u, t):
    return -a*u

I = 1; a = 2; T = 6
dt = float(sys.argv[1]) if len(sys.argv) >= 2 else 0.75
Nt = int(round(T/dt))
t = np.linspace(0, Nt*dt, Nt+1)

solvers = [odespy.RK2(f),
           odespy.RK3(f),
           odespy.RK4(f),]

# BackwardEuler must use Newton solver to converge
# (Picard is default and leads to divergence)
solvers.append(
    odespy.BackwardEuler(f, nonlinear_solver='Newton'))
# Or tell BackwardEuler that it is a linear problem
solvers[-1] = odespy.BackwardEuler(f, f_is_linear=True,
                                   jac=lambda u, t: -a)]
legends = []
for solver in solvers:
    solver.set_initial_condition(I)
    u, t = solver.solve(t)

    plt.plot(t, u)
    plt.hold('on')
    legends.append(solver.__class__.__name__)

# Compare with exact solution plotted on a very fine mesh
t_fine = np.linspace(0, T, 10001)
u_e = I*np.exp(-a*t_fine)
plt.plot(t_fine, u_e, '-') # avoid markers by specifying line type
legends.append('exact')

plt.legend(legends)
plt.title('Time step: %g' % dt)
plt.show()

With the odespy.BackwardEuler method we must either tell that the problem is linear and provide the Jacobian of \(f(u,t)\), i.e., \(\partial f/\partial u\), as the jac argument, or we have to assume that \(f\) is nonlinear, but then specify Newton’s method as solver for the nonlinear equations (since the equations are linear, Newton’s method will converge in one iteration). By default, odespy.BackwardEuler assumes a nonlinear problem to be solved by Picard iteration, but that leads to divergence in the present problem.

Visualization tip

We use Matplotlib for plotting here, but one could alternatively import scitools.std as plt instead. Plain use of Matplotlib as done here results in curves with different colors, which may be hard to distinguish on black-and-white paper. Using scitools.std, curves are automatically given colors and markers, thus making curves easy to distinguish on screen with colors and on black-and-white paper. The automatic adding of markers is normally a bad idea for a very fine mesh since all the markers get cluttered, but scitools.std limits the number of markers in such cases. For the exact solution we use a very fine mesh, but in the code above we specify the line type as a solid line (-), which means no markers and just a color to be automatically determined by the backend used for plotting (Matplotlib by default, but scitools.std gives the opportunity to use other backends to produce the plot, e.g., Gnuplot or Grace).

Also note the that the legends are based on the class names of the solvers, and in Python the name of the class type (as a string) of an object obj is obtained by obj.__class__.__name__.

Behavior of different schemes for the decay equation

The runs in Figure Behavior of different schemes for the decay equation and other experiments reveal that the 2nd-order Runge-Kutta method (RK2) is unstable for \(\Delta t>1\) and decays slower than the Backward Euler scheme for large and moderate \(\Delta t\) (see Exercise 13: Analyze explicit 2nd-order methods for an analysis). However, for fine \(\Delta t = 0.25\) the 2nd-order Runge-Kutta method approaches the exact solution faster than the Backward Euler scheme. That is, the latter scheme does a better job for larger \(\Delta t\), while the higher order scheme is superior for smaller \(\Delta t\). This is a typical trend also for most schemes for ordinary and partial differential equations.

The 3rd-order Runge-Kutta method (RK3) also has artifacts in the form of oscillatory behavior for the larger \(\Delta t\) values, much like that of the Crank-Nicolson scheme. For finer \(\Delta t\), the 3rd-order Runge-Kutta method converges quickly to the exact solution.

The 4th-order Runge-Kutta method (RK4) is slightly inferior to the Backward Euler scheme on the coarsest mesh, but is then clearly superior to all the other schemes. It is definitely the method of choice for all the tested schemes.

Remark about using the \(\theta\)-rule in Odespy

The Odespy package assumes that the ODE is written as \(u^{\prime}=f(u,t)\) with an \(f\) that is possibly nonlinear in \(u\). The \(\theta\)-rule for \(u^{\prime}=f(u,t)\) leads to

\[u^{n+1} = u^{n} + \Delta t\left(\theta f(u^{n+1}, t_{n+1}) + (1-\theta) f(u^{n}, t_{n})\right),\]

which is a nonlinear equation in \(u^{n+1}\). Odespy’s implementation of the \(\theta\)-rule (ThetaRule) and the specialized Backward Euler (BackwardEuler) and Crank-Nicolson (CrankNicolson) schemes must invoke iterative methods for solving the nonlinear equation in \(u^{n+1}\). This is done even when \(f\) is linear in \(u\), as in the model problem \(u^{\prime}=-au\), where we can easily solve for \(u^{n+1}\) by hand. Therefore, we need to specify use of Newton’s method to solve the equations. (Odespy allows other methods than Newton’s to be used, for instance Picard iteration, but that method is not suitable. The reason is that it applies the Forward Euler scheme to generate a start value for the iterations. Forward Euler may give very wrong solutions for large \(\Delta t\) values. Newton’s method, on the other hand, is insensitive to the start value in linear problems.)

Example: Adaptive Runge-Kutta methods

Odespy also offers solution methods that can adapt the size of \(\Delta t\) with time to match a desired accuracy in the solution. Intuitively, small time steps will be chosen in areas where the solution is changing rapidly, while larger time steps can be used where the solution is slowly varying. Some kind of error estimator is used to adjust the next time step at each time level.

A very popular adaptive method for solving ODEs is the Dormand-Prince Runge-Kutta method of order 4 and 5. The 5th-order method is used as a reference solution and the difference between the 4th- and 5th-order methods is used as an indicator of the error in the numerical solution. The Dormand-Prince method is the default choice in MATLAB’s widely used ode45 routine.

We can easily set up Odespy to use the Dormand-Prince method and see how it selects the optimal time steps. To this end, we request only one time step from \(t=0\) to \(t=T\) and ask the method to compute the necessary non-uniform time mesh to meet a certain error tolerance. The code goes like

import odespy
import numpy as np
import decay_mod
import sys
#import matplotlib.pyplot as plt
import scitools.std as plt

def f(u, t):
    return -a*u

def exact_solution(t):
    return I*np.exp(-a*t)

I = 1; a = 2; T = 5
tol = float(sys.argv[1])
solver = odespy.DormandPrince(f, atol=tol, rtol=0.1*tol)

Nt = 1  # just one step - let the scheme find its intermediate points
t_mesh = np.linspace(0, T, Nt+1)
t_fine = np.linspace(0, T, 10001)

solver.set_initial_condition(I)
u, t = solver.solve(t_mesh)

# u and t will only consist of [I, u^Nt] and [0,T]
# solver.u_all and solver.t_all contains all computed points
plt.plot(solver.t_all, solver.u_all, 'ko')
plt.hold('on')
plt.plot(t_fine, exact_solution(t_fine), 'b-')
plt.legend(['tol=%.0E' % tol, 'exact'])
plt.savefig('tmp_odespy_adaptive.png')
plt.show()

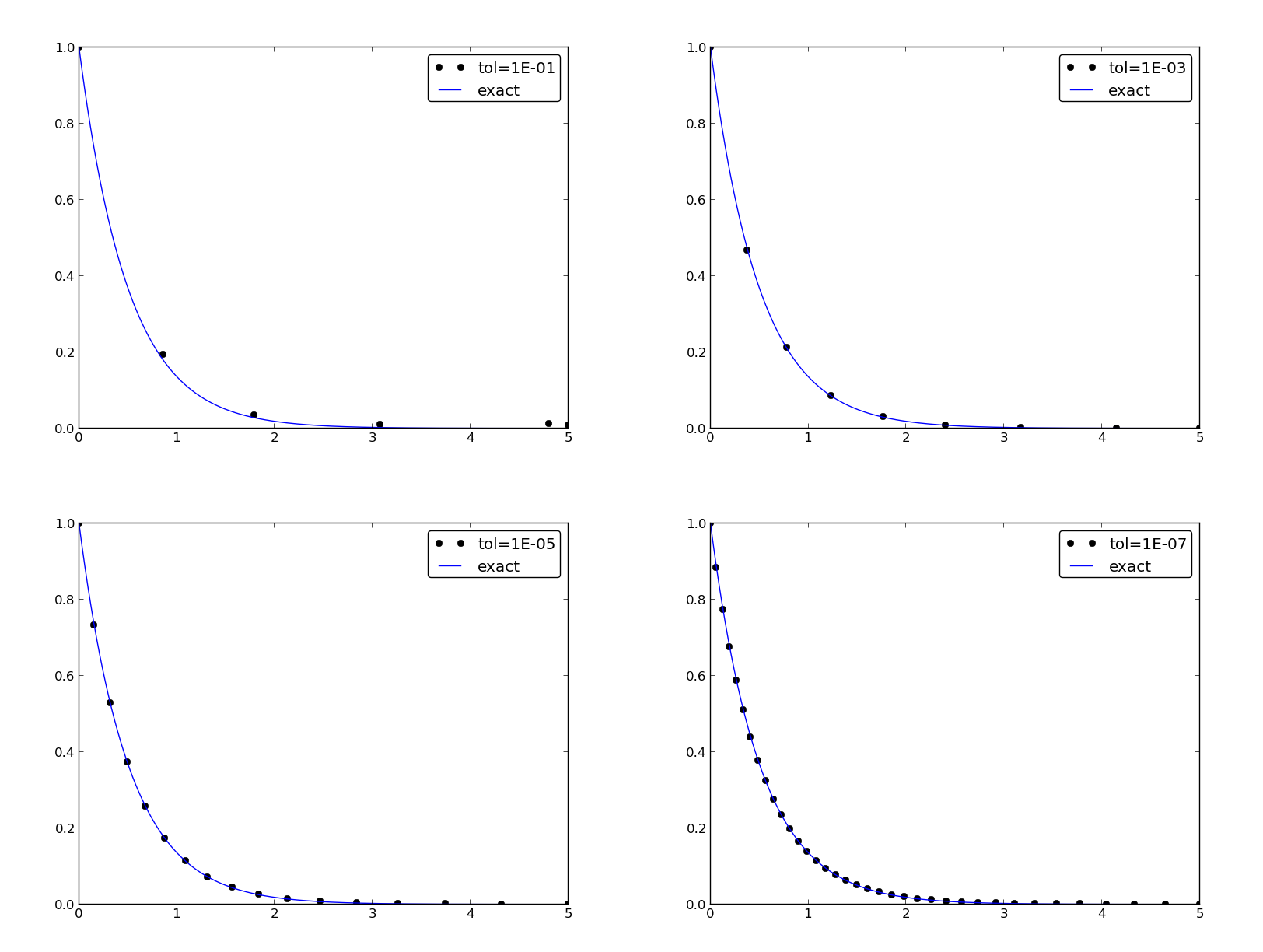
Running four cases with tolerances \(10^{-1}\), \(10^{-3}\), \(10^{-5}\), and \(10^{-7}\), gives the results in Figure Choice of adaptive time mesh by the Dormand-Prince method for different tolerances. Intuitively, one would expect denser points in the beginning of the decay and larger time steps when the solution flattens out.

Choice of adaptive time mesh by the Dormand-Prince method for different tolerances

Exercises (3)

Exercise 9: Experiment with precision in tests and the size of \(u\)

It is claimed in the section Verification via manufactured solutions that most numerical methods will reproduce a linear exact solution to machine precision. Test this assertion using the test function test_linear_solution in the decay_vc.py program. Vary the parameter c from very small, via c=1 to many larger values, and print out the maximum difference between the numerical solution and the exact solution. What is the relevant value of the tolerance in the float comparison in each case? Filename: test_precision.

Exercise 10: Implement the 2-step backward scheme

Implement the 2-step backward method (12) for the model \(u^{\prime}(t) = -a(t)u(t) + b(t)\), \(u(0)=I\). Allow the first step to be computed by either the Backward Euler scheme or the Crank-Nicolson scheme. Verify the implementation by choosing \(a(t)\) and \(b(t)\) such that the exact solution is linear in \(t\) (see the section Verification via manufactured solutions). Show mathematically that a linear solution is indeed a solution of the discrete equations.

Compute convergence rates (see the section Computing convergence rates) in a test case using \(a=\hbox{const}\) and \(b=0\), where we easily have an exact solution, and determine if the choice of a first-order scheme (Backward Euler) for the first step has any impact on the overall accuracy of this scheme. The expected error goes like \({\mathcal{O}(\Delta t^2)}\). Filename: decay_backward2step.

Exercise 11: Implement the 2nd-order Adams-Bashforth scheme

Implement the 2nd-order Adams-Bashforth method (18) for the decay problem \(u^{\prime}=-a(t)u + b(t)\), \(u(0)=I\), \(t\in (0, T]\). Use the Forward Euler method for the first step such that the overall scheme is explicit. Verify the implementation using an exact solution that is linear in time. Analyze the scheme by searching for solutions \(u^n=A^n\) when \(a=\hbox{const}\) and \(b=0\). Compare this second-order secheme to the Crank-Nicolson scheme. Filename: decay_AdamsBashforth2.

Exercise 12: Implement the 3rd-order Adams-Bashforth scheme

Implement the 3rd-order Adams-Bashforth method (19) for the decay problem \(u^{\prime}=-a(t)u + b(t)\), \(u(0)=I\), \(t\in (0, T]\). Since the scheme is explicit, allow it to be started by two steps with the Forward Euler method. Investigate experimentally the case where \(b=0\) and \(a\) is a constant: Can we have oscillatory solutions for large \(\Delta t\)? Filename: decay_AdamsBashforth3.

Exercise 13: Analyze explicit 2nd-order methods

Show that the schemes (16) and (17) are identical in the case \(f(u,t)=-a\), where \(a>0\) is a constant. Assume that the numerical solution reads \(u^n=A^n\) for some unknown amplification factor \(A\) to be determined. Find \(A\) and derive stability criteria. Can the scheme produce oscillatory solutions of \(u^{\prime}=-au\)? Plot the numerical and exact amplification factor. Filename: decay_RK2_Taylor2.

Problem 14: Implement and investigate the Leapfrog scheme

A Leapfrog scheme for the ODE \(u^{\prime}(t) = -a(t)u(t) + b(t)\) is defined by

\[\lbrack D_{2t}u = -au+b\rbrack^n{\thinspace .}\]

A separate method is needed to compute \(u^1\). The Forward Euler scheme is a possible candidate.

a) Implement the Leapfrog scheme for the model equation. Plot the solution in the case \(a=1\), \(b=0\), \(I=1\), \(\Delta t = 0.01\), \(t\in [0,4]\). Compare with the exact solution \({u_{\small\mbox{e}}}(t)=e^{-t}\).

b) Show mathematically that a linear solution in \(t\) fulfills the Forward Euler scheme for the first step and the Leapfrog scheme for the subsequent steps. Use this linear solution to verify the implementation, and automate the verification through a test function.

Hint. It can be wise to automate the calculations such that it is easy to redo the calculations for other types of solutions. Here is a possible sympy function that takes a symbolic expression u (implemented as a Python function of t), fits the b term, and checks if u fulfills the discrete equations:

import sympy as sym

def analyze(u):
    t, dt, a = sym.symbols('t dt a')

    print 'Analyzing u_e(t)=%s' % u(t)
    print 'u(0)=%s' % u(t).subs(t, 0)

    # Fit source term to the given u(t)
    b = sym.diff(u(t), t) + a*u(t)
    b = sym.simplify(b)
    print 'Source term b:', b

    # Residual in discrete equations; Forward Euler step
    R_step1 = (u(t+dt) - u(t))/dt + a*u(t) - b
    R_step1 = sym.simplify(R_step1)
    print 'Residual Forward Euler step:', R_step1

    # Residual in discrete equations; Leapfrog steps
    R = (u(t+dt) - u(t-dt))/(2*dt) + a*u(t) - b
    R = sym.simplify(R)
    print 'Residual Leapfrog steps:', R

def u_e(t):
    return c*t + I

analyze(u_e)
# or short form: analyze(lambda t: c*t + I)

c) Show that a second-order polynomial in \(t\) cannot be a solution of the discrete equations. However, if a Crank-Nicolson scheme is used for the first step, a second-order polynomial solves the equations exactly.

d) Create a manufactured solution \(u(t)=\sin(t)\) for the ODE \(u^{\prime}=-au+b\). Compute the convergence rate of the Leapfrog scheme using this manufactured solution. The expected convergence rate of the Leapfrog scheme is \({\mathcal{O}(\Delta t^2)}\). Does the use of a 1st-order method for the first step impact the convergence rate?

e) Set up a set of experiments to demonstrate that the Leapfrog scheme (13) is associated with numerical artifacts (instabilities). Document the main results from this investigation.

f) Analyze and explain the instabilities of the Leapfrog scheme (13):

1. Choose \(a=\mbox{const}\) and \(b=0\). Assume that an exact solution of the discrete equations has the form \(u^n=A^n\), where \(A\) is an amplification factor to be determined. Derive an equation for \(A\) by inserting \(u^n=A^n\) in the Leapfrog scheme.
2. Compute \(A\) either by hand and/or with the aid of sympy. The polynomial for \(A\) has two roots, \(A_1\) and \(A_2\). Let \(u^n\) be a linear combination \(u^n=C_1A_1^n + C_2A_2^n\).
3. Show that one of the roots is the reason for instability.
4. Compare \(A\) with the exact expression, using a Taylor series approximation.
5. How can \(C_1\) and \(C_2\) be determined?

g) Since the original Leapfrog scheme is unconditionally unstable as time grows, it demands some stabilization. This can be done by filtering, where we first find \(u^{n+1}\) from the original Leapfrog scheme and then replace \(u^{n}\) by \(u^n + \gamma (u^{n-1} - 2u^n + u^{n+1})\), where \(\gamma\) can be taken as 0.6. Implement the filtered Leapfrog scheme and check that it can handle tests where the original Leapfrog scheme is unstable.

Filename: decay_leapfrog.

Problem 15: Make a unified implementation of many schemes

Consider the linear ODE problem \(u^{\prime}(t)=-a(t)u(t) + b(t)\), \(u(0)=I\). Explicit schemes for this problem can be written in the general form

(23)\[ u^{n+1} = \sum_{j=0}^m c_ju^{n-j},\]

for some choice of \(c_0,\ldots,c_m\). Find expressions for the \(c_j\) coefficients in case of the \(\theta\)-rule, the three-level backward scheme, the Leapfrog scheme, the 2nd-order Runge-Kutta method, and the 3rd-order Adams-Bashforth scheme.

Make a class ExpDecay that implements the general updating formula (23). The formula cannot be applied for \(n < m\), and for those \(n\) values, other schemes must be used. Assume for simplicity that we just repeat Crank-Nicolson steps until (23) can be used. Use a subclass to specify the list \(c_0,\ldots,c_m\) for a particular method, and implement subclasses for all the mentioned schemes. Verify the implementation by testing with a linear solution, which should be exactly reproduced by all methods. Filename: decay_schemes_unified.