Study guide: Approximation of functions
2016
Finite elements can handle complex geometry, adaptive meshes, higher-order approximations and has a firm theory
- Can with ease solve PDEs in domains with complex geometry
- Can with ease create varying spatial resolution to get accuracy where it is needed
- Can with ease provide higher-order approximations
- Has a rigorous mathematical analysis framework

A dolphin and its flow
Solving PDEs by the finite element method
- Transform the PDE problem to a variational form
- Define function approximation over finite elements
- Use a computational machinery to derive linear systems
- Solve linear systems
- Finite elements in space
- Finite difference (or ODE solver) in time
We start with function approximation, then we treat PDEs
- Start with approximation of functions, not PDEs
- Introduce finite element approximations
- See later how this machinery is applied to PDEs
The finite element method has many concepts and a jungle of details. This learning strategy minimizes the mixing of ideas, concepts, and technical details.
Find a vector in some space that approximates a given vector in a space of higher dimension

The approximation is a linear combination of prescribed basis functions
General idea of finding an approximation \( u(x) \) to some given \( f(x) \):
$$ u(x) = \sum_{i=0}^N c_i\baspsi_i(x) $$
where
- \( \baspsi_i(x) \) are prescribed functions
- \( c_i \), \( i=0,\ldots,N \) are unknown coefficients to be determined
We have three methods to determine the coefficients
We shall address three approaches:
- The least squares method
- The projection (or Galerkin) method
- The interpolation (or collocation) method
Our mathematical framework for doing this is phrased in a way such that it becomes easy to understand and use the FEniCS software package for finite element computing.
Approximation of planar vectors; problem
Given a vector \( \f = (3,5) \), find an approximation to \( \f \) directed along a given line.

Approximation of planar vectors; vector space terminology
$$ V = \mbox{span}\,\{ \psib_0\} $$
- \( \psib_0 \) is a basis vector in the space \( V \)
- Seek \( \u = c_0\psib_0\in V \)
- Determine \( c_0 \) such that \( \u \) is the "best" approximation to \( \f \)
- Visually, "best" is obvious
Define
- the error \( \e = \f - \u \)
- the (Eucledian) scalar product of two vectors: \( (\u,\v) \)
- the norm of \( \e \): \( ||\e|| = \sqrt{(\e, \e)} \)
The least squares method; principle
- Idea: find \( c_0 \) such that \( ||\e|| \) is minimized
- Mathematical convenience: minimize \( E=||\e||^2 \)
$$
\begin{equation*}
\frac{\partial E}{\partial c_0} = 0
\end{equation*}
$$
The least squares method; calculations
$$
\begin{align*}
E(c_0) &= (\e,\e) = (\f - \u, \f - \u) = (\f - c_0\psib_0, \f - c_0\psib_0)\\
&= (\f,\f) - 2c_0(\f,\psib_0) + c_0^2(\psib_0,\psib_0)
\end{align*}
$$
$$
\begin{equation}
\frac{\partial E}{\partial c_0} = -2(\f,\psib_0) + 2c_0 (\psib_0,\psib_0) = 0
\tag{1}
\end{equation}
$$
$$
c_0 = \frac{(\f,\psib_0)}{(\psib_0,\psib_0)} = \frac{3a + 5b}{a^2 + b^2}
$$
Observation to be used later: the vanishing derivative (1) can be alternatively written as
$$ (\e, \psib_0) = 0 $$
The projection (or Galerkin) method
- Last slide: \( \min E \) is equivalent with \( (\e, \psib_0)=0 \)
- \( (\e, \psib_0)=0 \) implies \( (\e, \v)=0 \) for any \( \v\in V \)
- That is: instead of using the least-squares principle, we can
require that \( \e \) is orthogonal to any \( \v\in V \)
(visually clear, but can easily be computed too) - Precise math: find \( c_0 \) such that \( (\e, \v) = 0,\quad\forall\v\in V \)
- Equivalent (see notes): find \( c_0 \) such that \( (\e, \psib_0)=0 \)
- Insert \( \e = \f - c_0\psib_0 \) and solve for \( c_0 \)
- Same equation for \( c_0 \) and hence same solution as in the least squares method
Approximation of general vectors
Given a vector \( \f \), find an approximation \( \u\in V \):
$$
\begin{equation*}
V = \hbox{span}\,\{\psib_0,\ldots,\psib_N\}
\end{equation*}
$$
We have a set of linearly independent basis vectors \( \psib_0,\ldots,\psib_N \). Any \( \u\in V \) can then be written as
$$ \u = \sum_{j=0}^Nc_j\psib_j$$
The least squares method
Idea: find \( c_0,\ldots,c_N \) such that \( E= ||\e||^2 \) is minimized, \( \e=\f-\u \).
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (\e,\e) = (\f -\sum_jc_j\psib_j,\f -\sum_jc_j\psib_j)
\nonumber\\
&= (\f,\f) - 2\sum_{j=0}^Nc_j(\f,\psib_j) +
\sum_{p=0}^N\sum_{q=0}^N c_pc_q(\psib_p,\psib_q)
\end{align*}
$$
$$
\begin{equation*}
\frac{\partial E}{\partial c_i} = 0,\quad i=0,\ldots,N
\end{equation*}
$$
After some work we end up with a linear system
$$
\begin{align}
\sum_{j=0}^N A_{i,j}c_j &= b_i,\quad i=0,\ldots,N
\tag{2}\\
A_{i,j} &= (\psib_i,\psib_j)
\tag{3}\\
b_i &= (\psib_i, \f)
\tag{4}
\end{align}
$$
The projection (or Galerkin) method
Can be shown that minimizing \( ||\e|| \) implies that \( \e \) is orthogonal to all \( \v\in V \):
$$
(\e,\v)=0,\quad \forall\v\in V
$$
which implies that \( \e \) most be orthogonal to each basis vector:
$$ (\e,\psib_i)=0,\quad i=0,\ldots,N $$
This orthogonality condition is the principle of the projection (or Galerkin) method. Leads to the same linear system as in the least squares method.
Approximation of a function in a function space
Let \( V \) be a function space spanned by a set of basis functions \( \baspsi_0,\ldots,\baspsi_N \),
$$
\begin{equation*}
V = \hbox{span}\,\{\baspsi_0,\ldots,\baspsi_N\}
\end{equation*}
$$
Find \( u\in V \) as a linear combination of the basis functions:
$$ u = \sum_{j\in\If} c_j\baspsi_j,\quad\If = \{0,1,\ldots,N\} $$
The least squares method can be extended from vectors to functions
As in the vector case, minimize the (square) norm of the error, \( E \), with respect to the coefficients \( c_j \), \( j\in\If \):
$$
E = (e,e) = (f-u,f-u) = \left(f(x)-\sum_{j\in\If} c_j\baspsi_j(x), f(x)-\sum_{j\in\If} c_j\baspsi_j(x)\right)
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
But what is the scalar product when \( \baspsi_i \) is a function?
$$(f,g) = \int_\Omega f(x)g(x)\, dx$$
(natural extension from Eucledian product \( (\u, \v) = \sum_j u_jv_j \))
The least squares method; details
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (e,e) = (f-u,f-u) \\
&= (f,f) -2\sum_{j\in\If} c_j(f,\baspsi_i)
+ \sum_{p\in\If}\sum_{q\in\If} c_pc_q(\baspsi_p,\baspsi_q)
\end{align*}
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
The computations are identical to the vector case, and consequently we get a linear system
$$
\sum_{j\in\If} A_{i,j}c_j = b_i,\ i\in\If,\quad
A_{i,j} = (\baspsi_i,\baspsi_j),\
b_i = (f,\baspsi_i)
$$
The projection (or Galerkin) method
As before, minimizing \( (e,e) \) is equivalent to
$$
(e,\baspsi_i)=0,\quad i\in\If
\tag{5}
$$
which is equivalent to
$$
(e,v)=0,\quad\forall v\in V
\tag{6}
$$
which is the projection (or Galerkin) method.
The algebra is the same as in the multi-dimensional vector case, and we get the same linear system as arose from the least squares method.
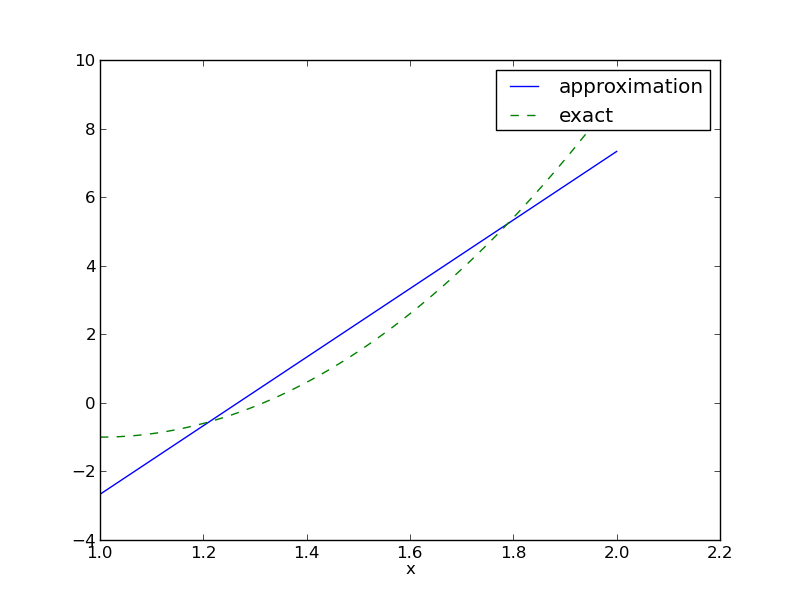
Example: fit a parabola by a straight line; problem
Approximate a parabola \( f(x) = 10(x-1)^2 - 1 \) by a straight line.
$$
\begin{equation*} V = \hbox{span}\,\{1, x\} \end{equation*}
$$
That is, \( \baspsi_0(x)=1 \), \( \baspsi_1(x)=x \), and \( N=1 \).
We seek
$$
\begin{equation*}
u=c_0\baspsi_0(x) + c_1\baspsi_1(x) = c_0 + c_1x
\end{equation*}
$$
Example: fit a parabola by a straight line; solution
$$
\begin{align*}
A_{0,0} &= (\baspsi_0,\baspsi_0) = \int_1^21\cdot 1\, dx = 1\\
A_{0,1} &= (\baspsi_0,\baspsi_1) = \int_1^2 1\cdot x\, dx = 3/2\\
A_{1,0} &= A_{0,1} = 3/2\\
A_{1,1} &= (\baspsi_1,\baspsi_1) = \int_1^2 x\cdot x\,dx = 7/3\\
b_1 &= (f,\baspsi_0) = \int_1^2 (10(x-1)^2 - 1)\cdot 1 \, dx = 7/3\\
b_2 &= (f,\baspsi_1) = \int_1^2 (10(x-1)^2 - 1)\cdot x\, dx = 13/3
\end{align*}
$$
Solution of 2x2 linear system:
$$ c_0 = -38/3,\quad c_1 = 10,\quad u(x) = 10x - \frac{38}{3} $$
Example: fit a parabola by a straight line; plot
Ideas for implementing the least squares method via symbolic computations
Consider symbolic computation of the linear system, where
- \( f(x) \) is given as a
sympyexpressionf(involving the symbolx), -
psiis a list of \( \sequencei{\baspsi} \), -
Omegais a 2-tuple/list holding the domain \( \Omega \)
Carry out the integrations, solve the linear system, and return \( u(x)=\sum_jc_j\baspsi_j(x) \)
Basic symbolic (SymPy) code for least squares
import sympy as sym
def least_squares(f, psi, Omega):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
for i in range(N+1):
for j in range(i, N+1):
A[i,j] = sym.integrate(psi[i]*psi[j],
(x, Omega[0], Omega[1]))
A[j,i] = A[i,j]
b[i,0] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i]
return u, c
Observe: symmetric coefficient matrix so we can halve the integrations.
Improved code if symbolic integration fails
- If
sym.integratefails, it returns ansym.Integralobject. We can test on this object and fall back on numerical integration. - We can include a boolean argument
symbolicto explicitly choose between symbolic and numerical computing.
def least_squares(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
for j in range(i, N+1):
integrand = psi[i]*psi[j]
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
# Could not integrate symbolically,
# fall back on numerical integration
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
A[i,j] = A[j,i] = I
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i,0] = I
...
Plotting of the solution
Compare \( f \) and \( u \) visually:
def comparison_plot(f, u, Omega, filename='tmp.pdf'):
x = sym.Symbol('x')
# Turn f and u to ordinary Python functions
f = sym.lambdify([x], f, modules="numpy")
u = sym.lambdify([x], u, modules="numpy")
resolution = 401 # no of points in plot
xcoor = linspace(Omega[0], Omega[1], resolution)
exact = f(xcoor)
approx = u(xcoor)
plot(xcoor, approx)
hold('on')
plot(xcoor, exact)
legend(['approximation', 'exact'])
savefig(filename)
All code in module approx1D.py
Application of the software: fit a parabola by a straight line
>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x], Omega=[1, 2])
>>> comparison_plot(f, u, Omega=[1, 2])

The approximation is exact if \( f\in V \)
- What if we add \( \baspsi_2=x^2 \) to the space \( V \)?
- That is, approximating a parabola by any parabola?
- (Hopefully we get the exact parabola!)
>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x, x**2], Omega=[1, 2])
>>> print u
10*x**2 - 20*x + 9
>>> print sym.expand(f)
10*x**2 - 20*x + 9
The general result: perfect approximation if \( f\in V \)
- What if we use \( \psi_i(x)=x^i \) for \( i=0,\ldots,N=40 \)?
- The output from
least_squaresis \( c_i=0 \) for \( i>2 \)
If \( f\in V \), least squares and projection/Galerkin give \( u=f \).
Proof of why \( f\in V \) gives exact \( u \)
If \( f\in V \), \( f=\sum_{j\in\If}d_j\baspsi_j \), for some \( \sequencei{d} \). Then
$$
\begin{equation*}
b_i = (f,\baspsi_i) = \sum_{j\in\If}d_j(\baspsi_j, \baspsi_i)
= \sum_{j\in\If} d_jA_{i,j}
\end{equation*}
$$
The linear system \( \sum_j A_{i,j}c_j = b_i \), \( i\in\If \), is then
$$
\begin{equation*}
\sum_{j\in\If}c_jA_{i,j} = \sum_{j\in\If}d_jA_{i,j},\quad i\in\If
\end{equation*}
$$
which implies that \( c_i=d_i \) for \( i\in\If \) and \( u \) is identical to \( f \).
Finite-precision in numerical computations; question
The previous computations were symbolic. What if we solve the linear system numerically with standard arrays?
That is, \( f \) is parabola, but we approximate with
$$ u(x) = c_0 + c_1x + c_2x^2 + c_3x^3 +\cdots + c_Nx^N $$
We expect \( c_2=c_3=\cdots=c_N=0 \) since \( f\in V \) implies \( u=f \).
Will we get this result with finite precision computer arithmetic?
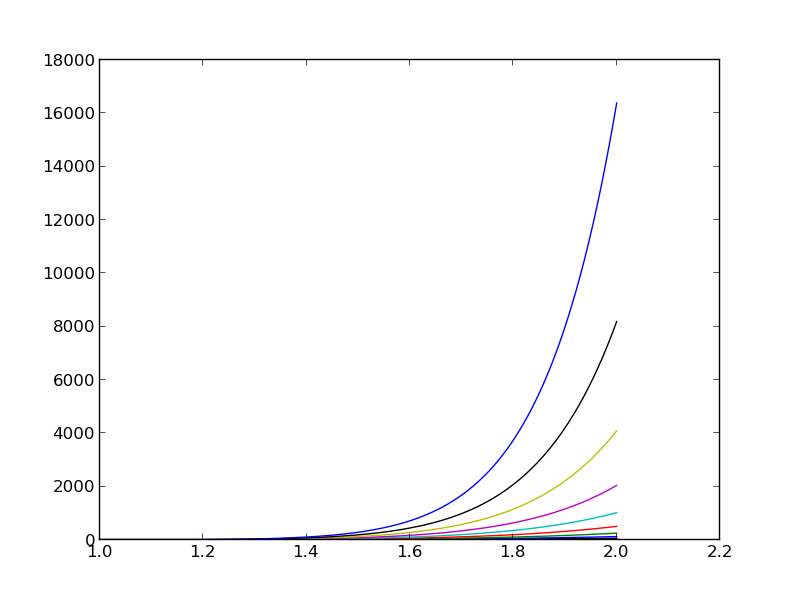
Finite-precision in numerical computations; results
| exact | sympy | numpy32 | numpy64 |
|---|---|---|---|
| 9 | 9.62 | 5.57 | 8.98 |
| -20 | -23.39 | -7.65 | -19.93 |
| 10 | 17.74 | -4.50 | 9.96 |
| 0 | -9.19 | 4.13 | -0.26 |
| 0 | 5.25 | 2.99 | 0.72 |
| 0 | 0.18 | -1.21 | -0.93 |
| 0 | -2.48 | -0.41 | 0.73 |
| 0 | 1.81 | -0.013 | -0.36 |
| 0 | -0.66 | 0.08 | 0.11 |
| 0 | 0.12 | 0.04 | -0.02 |
| 0 | -0.001 | -0.02 | 0.002 |
- Column 2:
matrixandlu_solvefromsympy.mpmath.fp - Column 3:
numpymatrix with 4-byte floats - Column 4:
numpymatrix with 8-byte floats
The ill-conditioning is due to almost linearly dependent basis functions for large \( N \)
- Significant round-off errors in the numerical computations (!)
- But if we plot the approximations they look good (!)
Source or problem: the \( x^i \) functions become almost linearly dependent as \( i \) grows:
Ill-conditioning: general conclusions
- Almost linearly dependent basis functions give almost singular matrices
- Such matrices are said to be ill conditioned, and Gaussian elimination is severely affected by round-off errors
- The basis \( 1, x, x^2, x^3, x^4, \ldots \) is a bad basis
- Polynomials are fine as basis, but the more orthogonal they are, \( (\baspsi_i,\baspsi_j)\approx 0 \), the better
Fourier series approximation; problem and code
Let's approximate \( f \) by a typical Fourier series expansion
$$ u(x) = \sum_i a_i\sin i\pi x = \sum_{j=0}^Nc_j\sin((j+1)\pi x) $$
which means that
$$
\begin{equation*}
V = \hbox{span}\,\{ \sin \pi x, \sin 2\pi x,\ldots,\sin (N+1)\pi x\}
\end{equation*}
$$
Computations using the least_squares function:
N = 3
from sympy import sin, pi
psi = [sin(pi*(i+1)*x) for i in range(N+1)]
f = 10*(x-1)**2 - 1
Omega = [0, 1]
u, c = least_squares(f, psi, Omega)
comparison_plot(f, u, Omega)
Fourier series approximation; plot
Left: \( N=3 \), right: \( N=11 \):
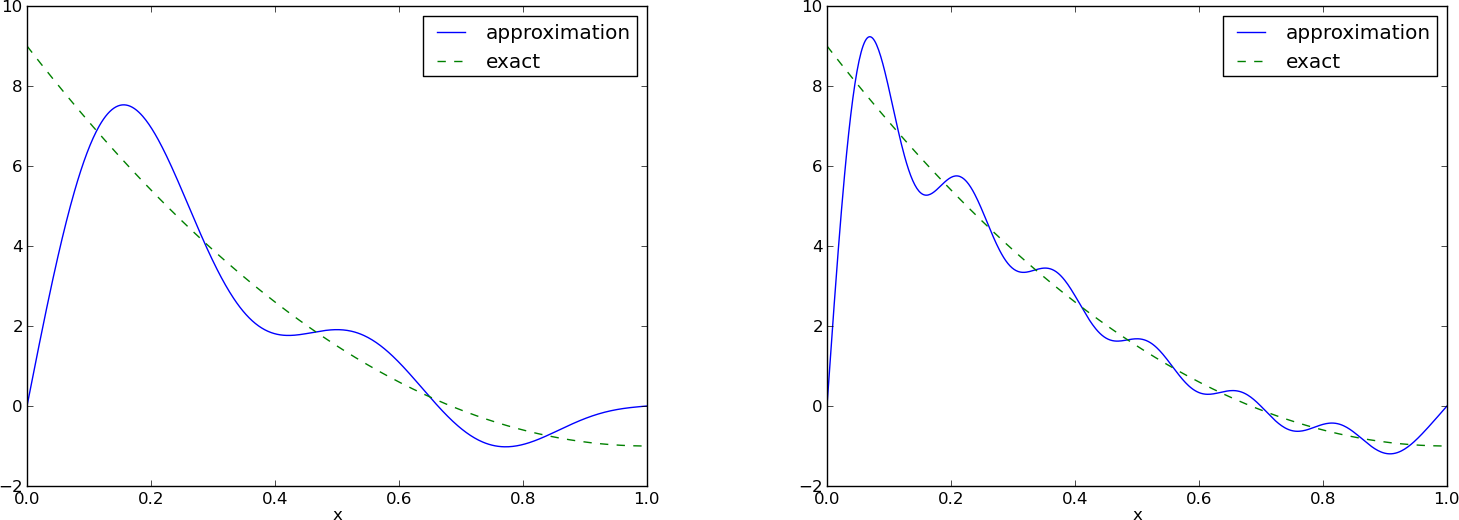
All \( \baspsi_i(0)=0 \) and hence \( u(0)=0 \neq f(0)=9 \). Similar problem at \( x=1 \). The boundary values of \( u \) are always wrong!
Fourier series approximation; improvements
- Considerably improvement with \( N=11 \), but still undesired discrepancy at \( x=0 \) and \( x=1 \)
- Possible remedy: add a term that leads to correct boundary values
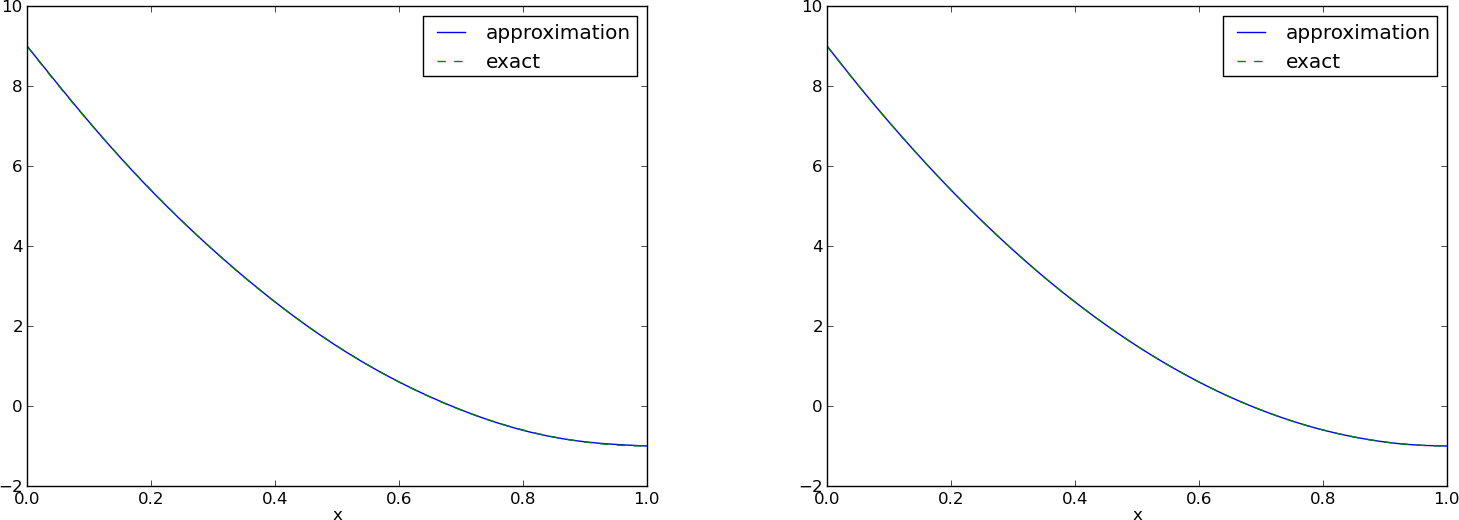
$$ u(x) = {\color{red}f(0)(1-x) + xf(1)} + \sum_{j\in\If} c_j\baspsi_j(x) $$
The extra terms ensure \( u(0)=f(0) \) and \( u(1)=f(1) \) and
is a strikingly good help to get a good
approximation!
Fourier series approximation; final results
\( N=3 \) vs \( N=11 \):
Orthogonal basis functions
This choice of sine functions as basis functions is popular because
- the basis functions are orthogonal: \( (\baspsi_i,\baspsi_j)=0 \)
- implying that \( A_{i,j} \) is a diagonal matrix
- implying that we can solve for \( c_i = 2\int_0^1 f(x)\sin ((i+1)\pi x) dx \)
- and what we get is the standard Fourier sine series of \( f \)
In general, for an orthogonal basis, \( A_{i,j} \) is diagonal and we can easily solve for \( c_i \):
$$
c_i = \frac{b_i}{A_{i,i}} = \frac{(f,\baspsi_i)}{(\baspsi_i,\baspsi_i)}
$$
Function for the least squares method with orthogonal basis functions
def least_squares_orth(f, psi, Omega):
N = len(psi) - 1
A = [0]*(N+1)
b = [0]*(N+1)
x = sym.Symbol('x')
for i in range(N+1):
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
b[i] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = [b[i]/A[i] for i in range(len(b))]
u = 0
for i in range(len(psi)):
u += c[i]*psi[i]
return u, c
Function for the least squares method with orthogonal basis functions; symbolic and numerical integration
Extensions:
- We can choose between symbolic or numerical integration (
symbolicargument). - If symbolic, we fall back on numerical integration after failure
(
sym.Integralis returned fromsym.integrate).
def least_squares_orth(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
# Diagonal matrix term
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
# Right-hand side term
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
print 'numerical integration of', integrand
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i] = I
...
Assumption above: \( \int_\Omega\basphi_i^2dx \) works symbolically (but there is no guarantee!)
The collocation or interpolation method; ideas and math
Here is another idea for approximating \( f(x) \) by \( u(x)=\sum_jc_j\baspsi_j \):
- Force \( u(\xno{i}) = f(\xno{i}) \) at some selected collocation points \( \sequencei{x} \)
- Then \( u \) is said to interpolate \( f \)
- The method is known as interpolation or collocation
$$ u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i})
\quad i\in\If,N
$$
This is a linear system with no need for integration:
$$
\begin{align}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If
\tag{7}\\
A_{i,j} &= \baspsi_j(\xno{i})
\tag{8}\\
b_i &= f(\xno{i})
\tag{9}
\end{align}
$$
No symmetric matrix: \( \baspsi_j(\xno{i})\neq \baspsi_i(\xno{j}) \) in general
The collocation or interpolation method; implementation
points holds the interpolation/collocation points
def interpolation(f, psi, points):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
# Turn psi and f into Python functions
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
A[i,j] = psi[j](points[i])
b[i,0] = f(points[i])
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i](x)
return u
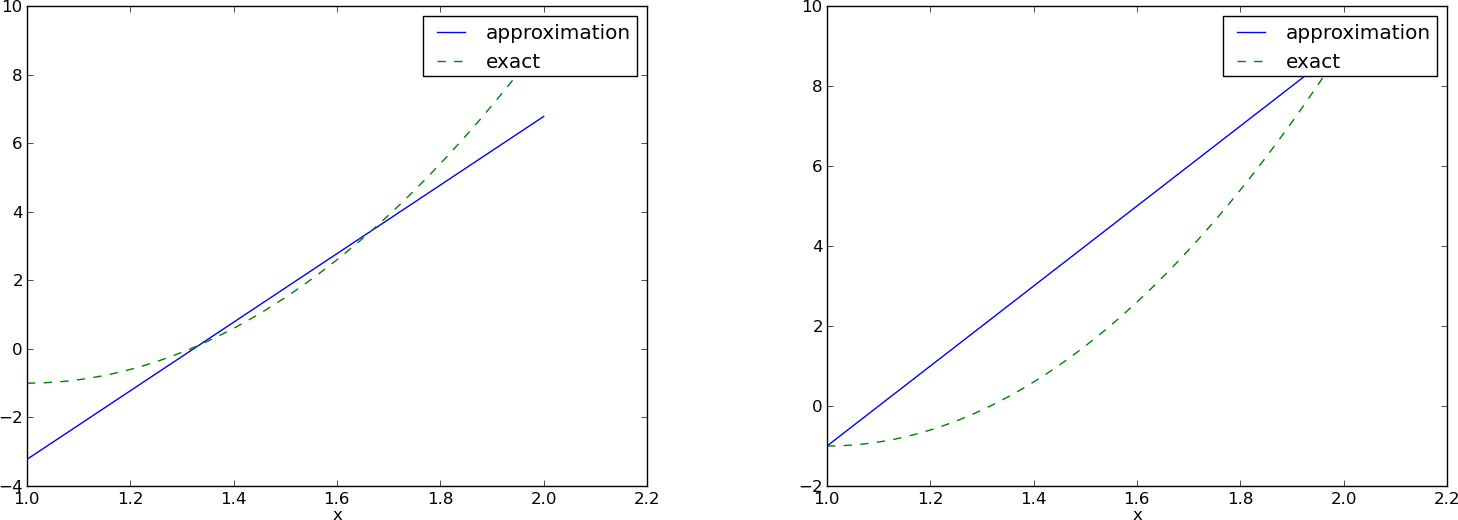
The collocation or interpolation method; approximating a parabola by linear functions
- Potential difficulty: how to choose \( \xno{i} \)?
- The results are sensitive to the points!
\( (4/3,5/3) \) vs \( (1,2) \):
The regression method
- Idea: Interpolation (collocation) method, but use \( m\gg N+1 \) points
- Problem: More equations than unknowns
- But this is well known as regression in statistics
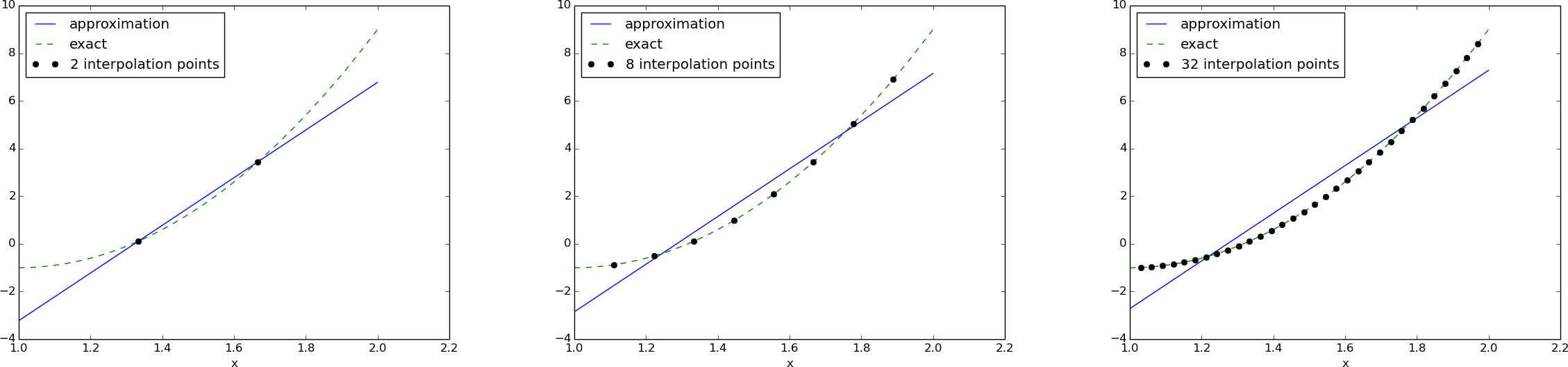
The regression method leads to an overdetermined linear system
Overdetermined linear system:
$$
u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i}),
\quad i=0,1,\ldots,m
$$
$$ \sum_{j\in\If} A_{i,j}c_j = b_i,\quad i=0,1,\ldots,m $$
$$ A_{i,j} = \baspsi_j(\xno{i}),\quad
b_i = f(\xno{i})$$
A least squares method is used to solve overdetermined linear systems
- Cannot (in general) solve \( Ac=b \) when there are more equations than unknowns
- Idea: Minimize \( r=b-Ac \) instead
- Result: the normal equations \( A^TAc=A^Tb \)
- \( (N+1)\times(N+1) \) system
- Write the normal equations as \( Bc=d \)
$$
\begin{align*}
B_{i,j} &= \sum_k A^T_{i,k}A_{k,j} = \sum_k A_{k,i}A_{k,j}
=\sum_{k=0}^m\baspsi_i(\xno{k})\baspsi_j(\xno{k})
\\
d_i &=\sum_k A^T_{i,k}b_k = \sum_k A_{k,i}b_k =\sum_{k=0}^m
\baspsi_i(\xno{k})f(\xno{k})
\end{align*}
$$
Implementation
def regression(f, psi, points):
N = len(psi) - 1
m = len(points)
# Use numpy arrays and numerical computing
B = np.zeros((N+1, N+1))
d = np.zeros(N+1)
# Wrap psi and f in Python functions rather than expressions
# so that we can evaluate psi at points[i]
x = sym.Symbol('x')
psi_sym = psi # save symbolic expression
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
B[i,j] = 0
for k in range(m+1):
B[i,j] += psi[i](points[k])*psi[j](points[k])
d[i] = 0
for k in range(m+1):
d[i] += psi[i](points[k])*f(points[k])
c = np.linalg.solve(B, d)
u = sum(c[i]*psi_sym[i] for i in range(N+1))
return u, c
Example on using the regression method; code
- Approximate \( f(x)=10(x-1)^2-1 \) by a linear function on \( \Omega=[1,2] \)
import sympy as sym
x = sym.Symbol('x')
f = 10*(x-1)**2 - 1
psi = [1, x]
Omega = [1, 2]
m_values = [2-1, 8-1, 64-1]
# Create m+3 points and use the inner m+1 points
for m in m_values:
points = np.linspace(Omega[0], Omega[1], m+3)[1:-1]
u, c = regression(f, psi, points)
comparison_plot(f, u, Omega, points=points,
points_legend='%d interpolation points' % (m+1))
Example on using the regression method; result
$$
\begin{align*}
u(x) &= 10x - 13.2,\quad 2\hbox{ points}\\
u(x) &= 10x - 12.7,\quad 8\hbox{ points}\\
u(x) &= 10x - 12.7,\quad 64\hbox{ points}
\end{align*}
$$

What is the regression method used for?
- It is one of the most dominating methods for approximating data in statistics
- Not so common for approximating functions
- Not much used for solving differential equations
- Recently very popular for statistical uncertainty quantification: approximating the mapping from input parameters to the solution via polynomials and the regression method (called polynomial chaos expansions)
Lagrange polynomials; motivation and ideas
Motivation:
- The interpolation/collocation method avoids integration
- With a diagonal matrix \( A_{i,j} = \baspsi_j(\xno{i}) \) we can solve the linear system by hand
The Lagrange interpolating polynomials \( \baspsi_j \) have the property that
$$ \baspsi_i(\xno{j}) =\delta_{ij},\quad \delta_{ij} =
\left\lbrace\begin{array}{ll}
1, & i=j\\
0, & i\neq j
\end{array}\right.
$$
Hence, \( c_i = f(x_i) \) and
$$
u(x) = \sum_{j\in\If} f(\xno{i})\baspsi_i(x)
$$
- Lagrange polynomials and interpolation/collocation look convenient
- Lagrange polynomials are very much used in the finite element method
Lagrange polynomials; formula and code
$$
\baspsi_i(x) =
\prod_{j=0,j\neq i}^N
\frac{x-\xno{j}}{\xno{i}-\xno{j}}
= \frac{x-x_0}{\xno{i}-x_0}\cdots\frac{x-\xno{i-1}}{\xno{i}-\xno{i-1}}\frac{x-\xno{i+1}}{\xno{i}-\xno{i+1}}
\cdots\frac{x-x_N}{\xno{i}-x_N}
$$
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
Lagrange polynomials; successful example

Lagrange polynomials; a less successful example
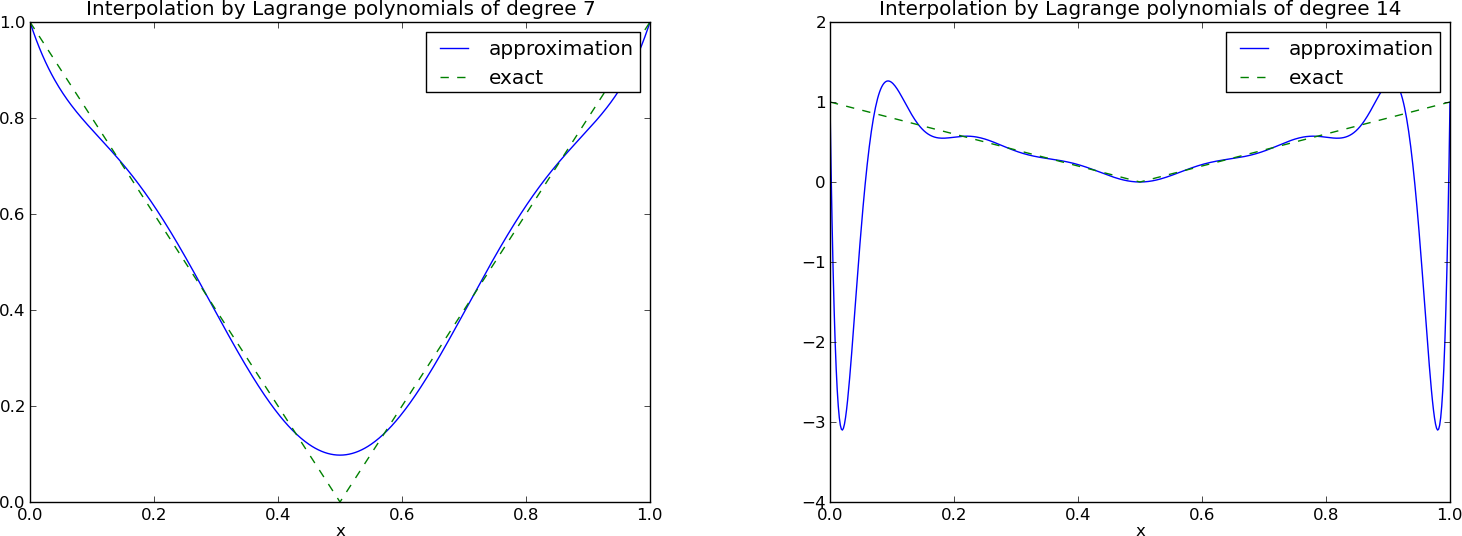
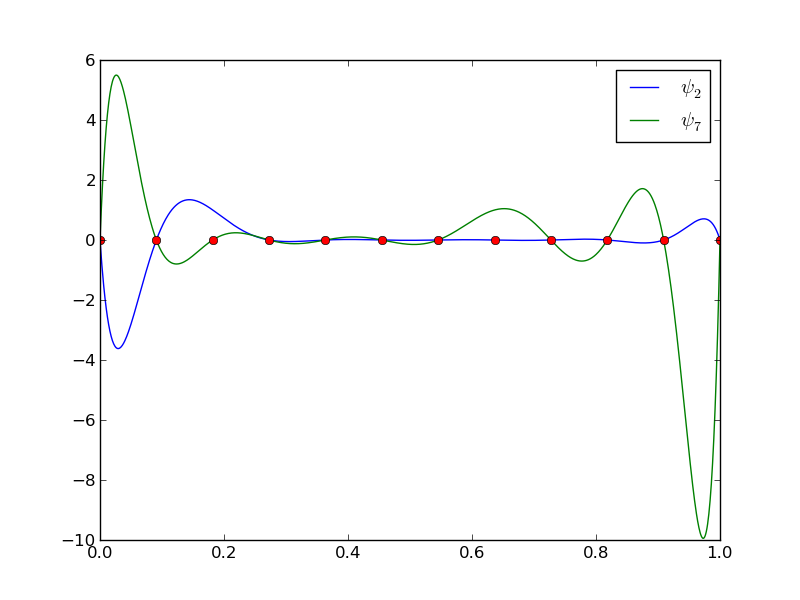
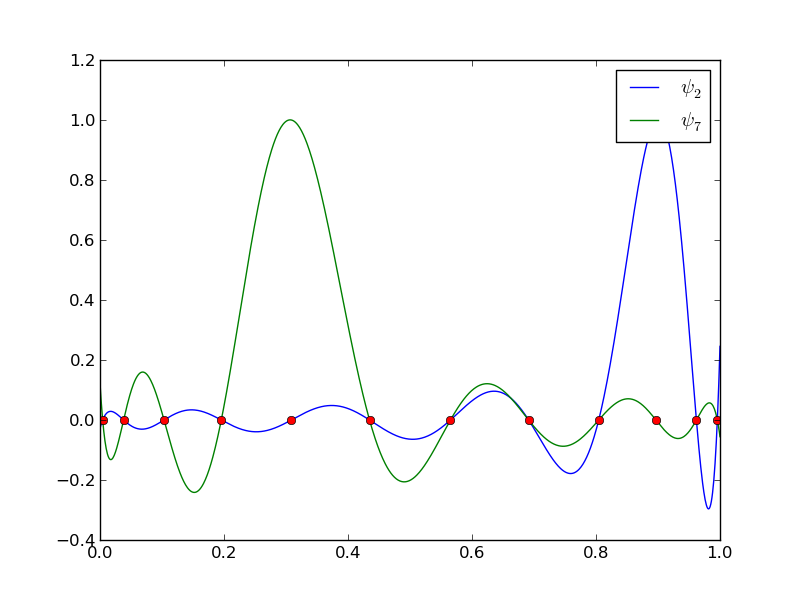
Lagrange polynomials; oscillatory behavior
12 points, degree 11, plot of two of the Lagrange polynomials - note that they are zero at all points except one.
Problem: strong oscillations near the boundaries for larger \( N \) values.
Lagrange polynomials; remedy for strong oscillations
The oscillations can be reduced by a more clever choice of interpolation points, called the Chebyshev nodes:
$$
\xno{i} = \half (a+b) + \half(b-a)\cos\left( \frac{2i+1}{2(N+1)}\pi\right),\quad i=0\ldots,N
$$
on an interval \( [a,b] \).
Lagrange polynomials; recalculation with Chebyshev nodes
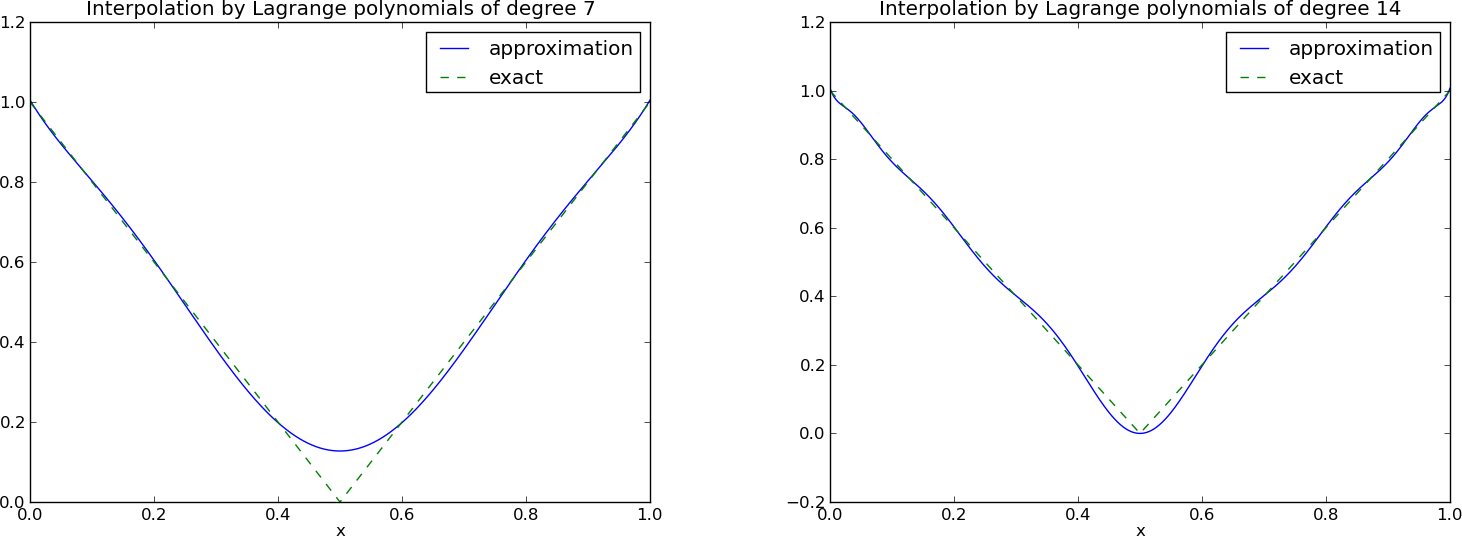
Lagrange polynomials; less oscillations with Chebyshev nodes
12 points, degree 11, plot of two of the Lagrange polynomials - note that they are zero at all points except one.
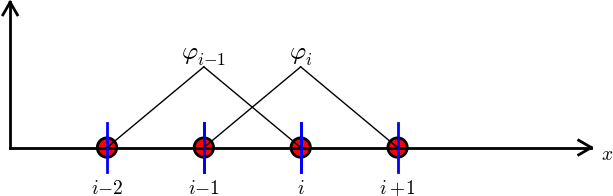
Finite element basis functions
The basis functions have so far been global: \( \baspsi_i(x) \neq 0 \) almost everywhere
In the finite element method we use basis functions with local support
- Local support: \( \baspsi_i(x) \neq 0 \) for \( x \) in a small subdomain of \( \Omega \)
- Typically hat-shaped
- \( u(x) \) based on these \( \baspsi_i \) is a piecewise polynomial defined over many (small) subdomains
- We introduce \( \basphi_i \) as the name of these finite element hat functions (and for now choose \( \baspsi_i=\basphi_i \))

The linear combination of hat functions is a piecewise linear function

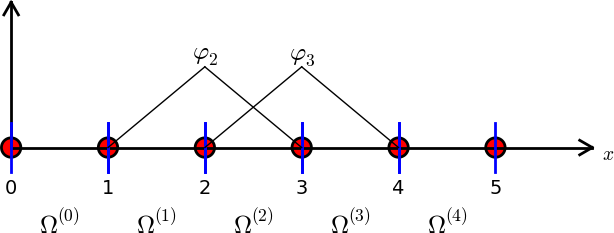
Elements and nodes
Split \( \Omega \) into \( N_e \) non-overlapping subdomains called elements:
$$
\Omega = \Omega^{(0)}\cup \cdots \cup \Omega^{(N_e)}
$$
On each element, introduce \( N_n \) points called nodes: \( \xno{0},\ldots,\xno{N_n-1} \)
- The finite element basis functions are named \( \basphi_i(x) \)
- \( \basphi_i=1 \) at node \( i \) and 0 at all other nodes
- \( \basphi_i \) is a Lagrange polynomial on each element
- For nodes at the boundary between two elements, \( \basphi_i \) is made up of a Lagrange polynomial over each element
Example on elements with two nodes (P1 elements)
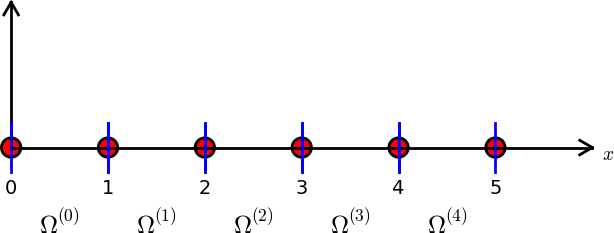
Data structure: nodes holds coordinates or nodes, elements holds the
node numbers in each element
nodes = [0, 1.2, 2.4, 3.6, 4.8, 5]
elements = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]]
Illustration of two basis functions on the mesh

Example on elements with three nodes (P2 elements)
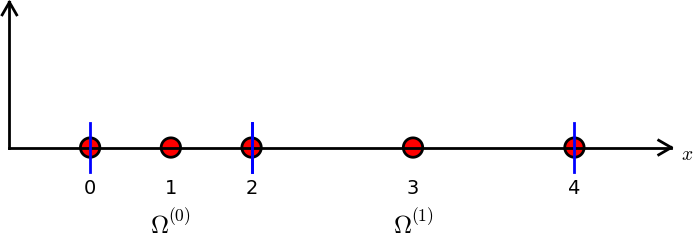
nodes = [0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1.0]
elements = [[0, 1, 2], [2, 3, 4], [4, 5, 6], [6, 7, 8]]
Some corresponding basis functions (P2 elements)
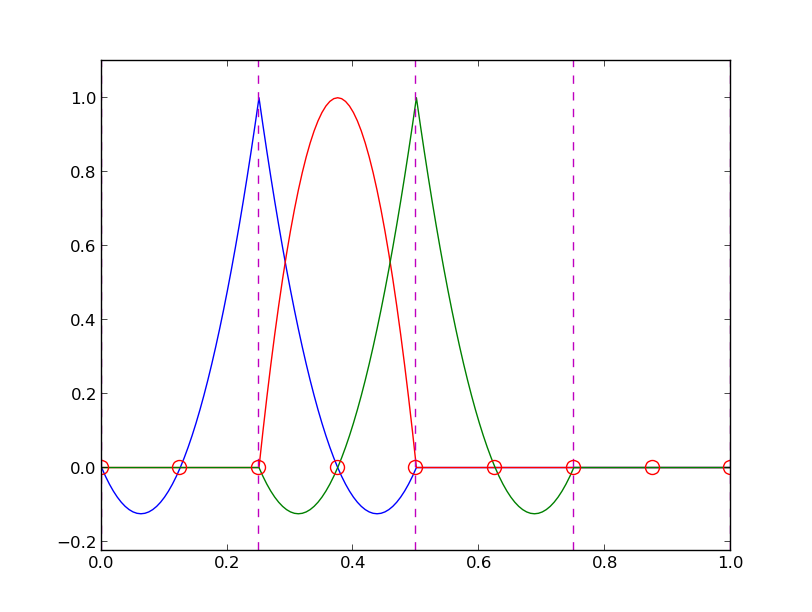
Examples on elements with four nodes (P3 elements)
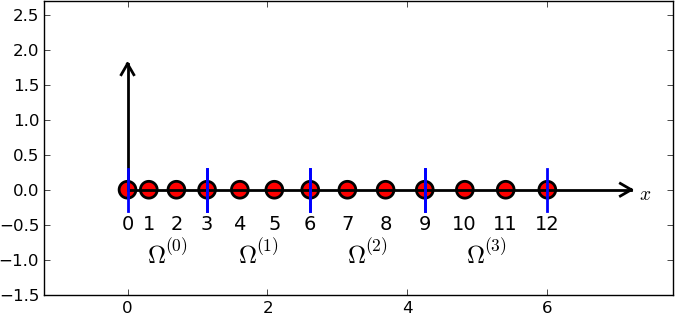
d = 3 # d+1 nodes per element
num_elements = 4
num_nodes = num_elements*d + 1
nodes = [i*0.5 for i in range(num_nodes)]
elements = [[i*d+j for j in range(d+1)] for i in range(num_elements)]
Some corresponding basis functions (P3 elements)
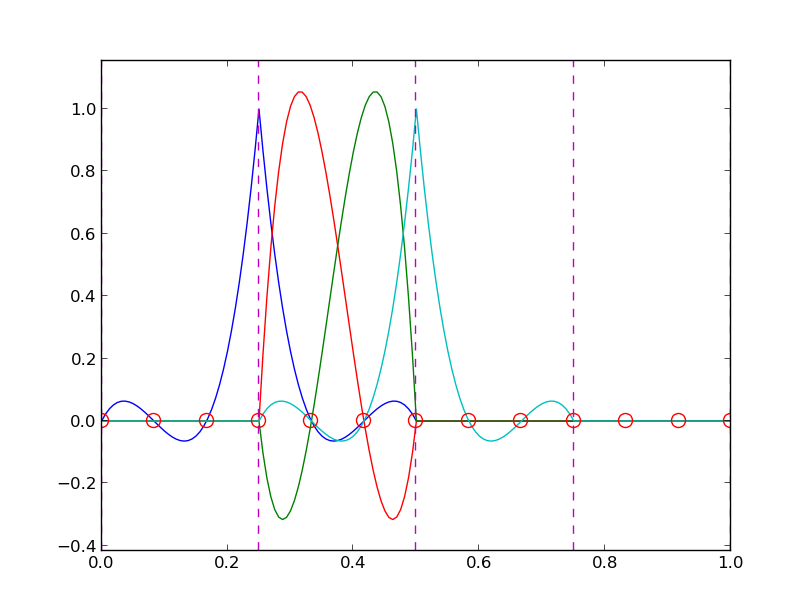
The numbering does not need to be regular from left to right
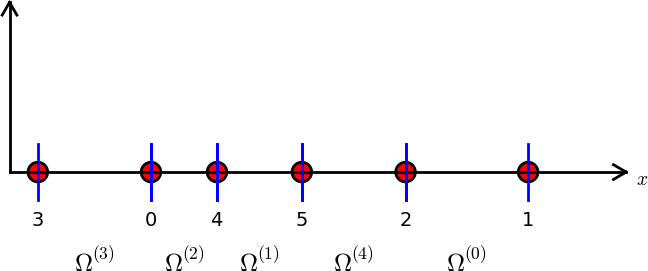
nodes = [1.5, 5.5, 4.2, 0.3, 2.2, 3.1]
elements = [[2, 1], [4, 5], [0, 4], [3, 0], [5, 2]]
Interpretation of the coefficients \( c_i \)
Important property: \( c_i \) is the value of \( u \) at node \( i \), \( \xno{i} \):
$$
u(\xno{i}) = \sum_{j\in\If} c_j\basphi_j(\xno{i}) =
c_i\basphi_i(\xno{i}) = c_i
$$
because \( \basphi_j(\xno{i}) =0 \) if \( i\neq j \) and \( \basphi_i(\xno{i}) =1 \)
Properties of the basis functions
- \( \basphi_i(x) \neq 0 \) only on those elements that contain global node \( i \)
- \( \basphi_i(x)\basphi_j(x) \neq 0 \) if and only if \( i \) and \( j \) are global node numbers in the same element
Since \( A_{i,j}=\int\basphi_i\basphi_j\dx \), most of the elements in the coefficient matrix will be zero
How to construct quadratic \( \basphi_i \) (P2 elements)

- Associate Lagrange polynomials with the nodes in an element
- When the polynomial is 1 on the element boundary, combine it with the polynomial in the neighboring element that is also 1 at the same point
Example on linear \( \basphi_i \) (P1 elements)
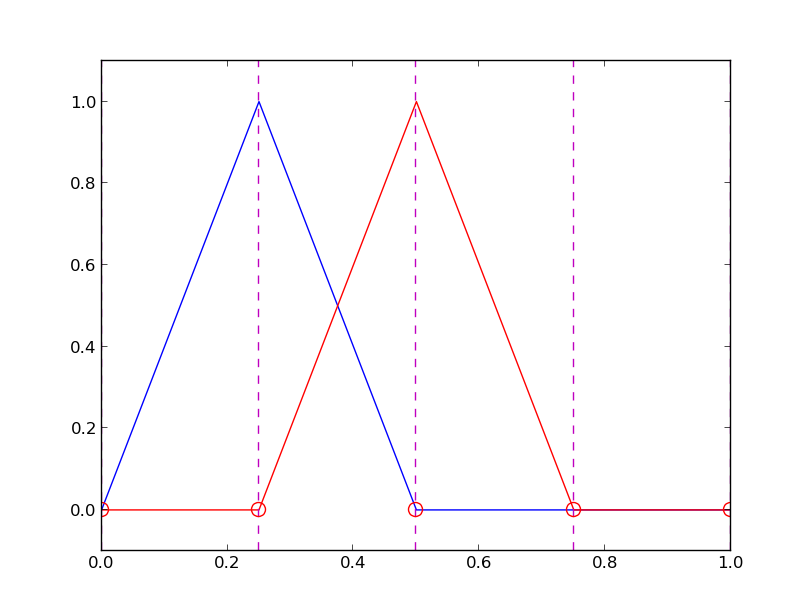
$$
\basphi_i(x) = \left\lbrace\begin{array}{ll}
0, & x < \xno{i-1}\\
(x - \xno{i-1})/h
& \xno{i-1} \leq x < \xno{i}\\
1 -
(x - x_{i})/h,
& \xno{i} \leq x < \xno{i+1}\\
0, & x\geq \xno{i+1}
\end{array}
\right.
$$
Example on cubic \( \basphi_i \) (P3 elements)

Calculating the linear system for \( c_i \)

Computing a specific matrix entry (1)

\( A_{2,3}=\int_\Omega\basphi_2\basphi_3 dx \): \( \basphi_2\basphi_3\neq 0 \) only over element 2. There,
$$ \basphi_3(x) = (x-x_2)/h,\quad \basphi_2(x) = 1- (x-x_2)/h$$
$$
A_{2,3} = \int_\Omega \basphi_2\basphi_{3}\dx =
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right) \frac{x - x_{2}}{h}
\dx = \frac{h}{6}
$$
Computing a specific matrix entry (2)

$$ A_{2,2} =
\int_{\xno{1}}^{\xno{2}}
\left(\frac{x - \xno{1}}{h}\right)^2\dx +
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right)^2\dx
= \frac{2h}{3}
$$
Calculating a general row in the matrix; figure

$$ A_{i,i-1} = \int_\Omega \basphi_i\basphi_{i-1}\dx = \hbox{?}$$
Calculating a general row in the matrix; details
$$
\begin{align*}
A_{i,i-1} &= \int_\Omega \basphi_i\basphi_{i-1}\dx\\
&=
\underbrace{\int_{\xno{i-2}}^{\xno{i-1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_i=0} +
\int_{\xno{i-1}}^{\xno{i}} \basphi_i\basphi_{i-1}\dx +
\underbrace{\int_{\xno{i}}^{\xno{i+1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_{i-1}=0}\\
&= \int_{\xno{i-1}}^{\xno{i}}
\underbrace{\left(\frac{x - x_{i}}{h}\right)}_{\basphi_i(x)}
\underbrace{\left(1 - \frac{x - \xno{i-1}}{h}\right)}_{\basphi_{i-1}(x)} \dx =
\frac{h}{6}
\end{align*}
$$
- \( A_{i,i+1}=A_{i,i-1} \) due to symmetry
- \( A_{i,i}=2h/3 \) (same calculation as for \( A_{2,2} \))
- \( A_{0,0}=A_{N,N}=h/3 \) (only one element)
Calculation of the right-hand side
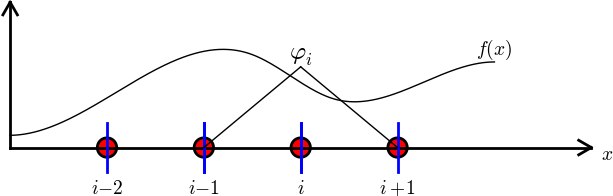
$$
b_i = \int_\Omega\basphi_i(x)f(x)\dx
= \int_{\xno{i-1}}^{\xno{i}} \frac{x - \xno{i-1}}{h} f(x)\dx
+ \int_{x_{i}}^{\xno{i+1}} \left(1 - \frac{x - x_{i}}{h}\right) f(x)
\dx
$$
Need a specific \( f(x) \) to do more...
Specific example with two elements; linear system and solution
- \( f(x)=x(1-x) \) on \( \Omega=[0,1] \)
- Two equal-sized elements \( [0,0.5] \) and \( [0.5,1] \)
$$
\begin{equation*}
A = \frac{h}{6}\left(\begin{array}{ccc}
2 & 1 & 0\\
1 & 4 & 1\\
0 & 1 & 2
\end{array}\right),\quad
b = \frac{h^2}{12}\left(\begin{array}{c}
2 - 3h\\
12 - 14h\\
10 -17h
\end{array}\right)
\end{equation*}
$$
$$
\begin{equation*} c_0 = \frac{h^2}{6},\quad c_1 = h - \frac{5}{6}h^2,\quad
c_2 = 2h - \frac{23}{6}h^2
\end{equation*}
$$
Specific example with two elements; plot
$$
\begin{equation*} u(x)=c_0\basphi_0(x) + c_1\basphi_1(x) + c_2\basphi_2(x)\end{equation*}
$$
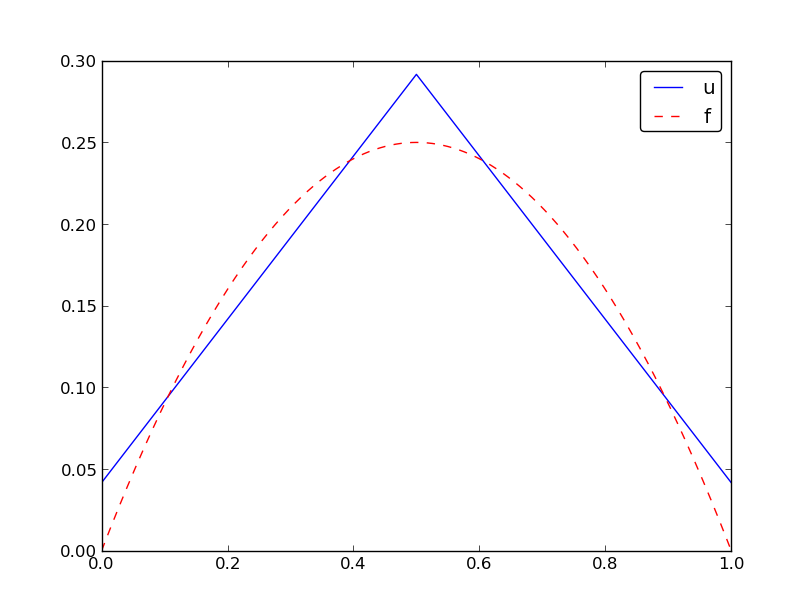
Specific example with four elements; plot

Specific example: what about P2 elements?
Assembly of elementwise computations
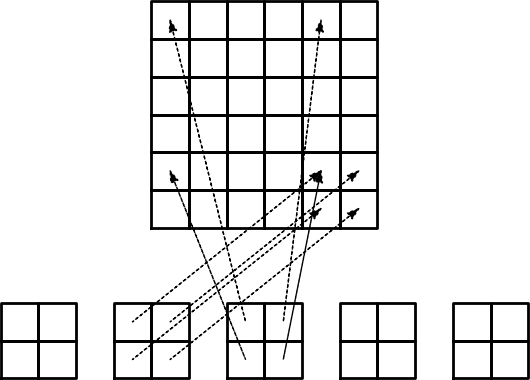
Split the integrals into elementwise integrals
$$
A_{i,j} = \int_\Omega\basphi_i\basphi_jdx =
\sum_{e} \int_{\Omega^{(e)}} \basphi_i\basphi_jdx,\quad
A^{(e)}_{i,j}=\int_{\Omega^{(e)}} \basphi_i\basphi_jdx
$$
Important observations:
- \( A^{(e)}_{i,j}\neq 0 \) if and only if \( i \) and \( j \) are nodes in element \( e \) (otherwise no overlap between the basis functions)
- All the nonzero elements in \( A^{(e)}_{i,j} \) are collected in an element matrix
- The element matrix has contributions from the \( \basphi_i \) functions associated with the nodes in element
- It is convenient to introduce a local numbering of the nodes in an element: \( 0,1,\ldots,d \)

The element matrix and local vs global node numbers
$$
\tilde A^{(e)} = \{ \tilde A^{(e)}_{r,s}\},\quad
\tilde A^{(e)}_{r,s} =
\int_{\Omega^{(e)}}\basphi_{q(e,r)}\basphi_{q(e,s)}dx,
\quad r,s\in\Ifd=\{0,\ldots,d\}
$$
Now,
- \( r,s \) run over local node numbers in an element: \( 0, 1,\ldots, d \)
- \( i,j \) run over global node numbers \( i,j\in\If = \{0,1,\ldots,N\} \)
- \( i=q(e,r) \): mapping of local node number \( r \) in element
\( e \) to the global node number \( i \) (math equivalent to
i=elements[e][r]) - Add \( \tilde A^{(e)}_{r,s} \) into the global \( A_{i,j} \) (assembly)
$$
A_{q(e,r),q(e,s)} := A_{q(e,r),q(e,s)} + \tilde A^{(e)}_{r,s},\quad
r,s\in\Ifd
$$
Illustration of the matrix assembly: regularly numbered P1 elements
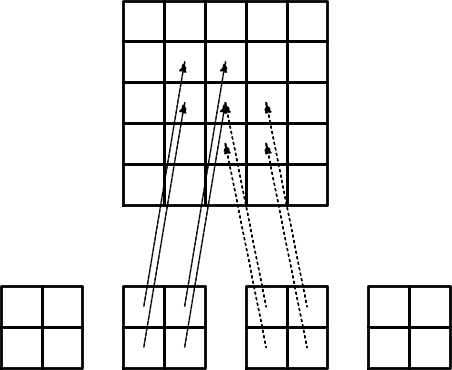
Illustration of the matrix assembly: regularly numbered P3 elements
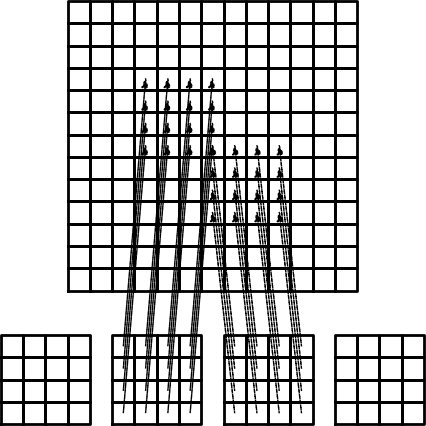
Illustration of the matrix assembly: irregularly numbered P1 elements

Assembly of the right-hand side
$$
b_i = \int_\Omega f(x)\basphi_i(x)dx =
\sum_{e} \int_{\Omega^{(e)}} f(x)\basphi_i(x)dx,\quad
b^{(e)}_{i}=\int_{\Omega^{(e)}} f(x)\basphi_i(x)dx
$$

Important observations:
- \( b_i^{(e)}\neq 0 \) if and only if global node \( i \) is a node in element \( e \) (otherwise \( \basphi_i=0 \))
- The \( d+1 \) nonzero \( b_i^{(e)} \) can be collected in an element vector \( \tilde b_r^{(e)}=\{ \tilde b_r^{(e)}\} \), \( r\in\Ifd \)
Assembly:
$$
b_{q(e,r)} := b_{q(e,r)} + \tilde b^{(e)}_{r},\quad
r\in\Ifd
$$
Mapping to a reference element
Instead of computing
$$
\begin{equation*} \tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
= \int_{x_L}^{x_R}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
\end{equation*}
$$
we now map \( [x_L, x_R] \) to
a standardized reference element domain \( [-1,1] \) with local coordinate \( X \)
We use affine mapping: linear stretch of \( X\in [-1,1] \) to \( x\in [x_L,x_R] \)
$$
x = \half (x_L + x_R) + \half (x_R - x_L)X
$$
or rewritten as
$$
x = x_m + {\half}hX, \qquad x_m=(x_L+x_R)/2,\quad h=x_R-x_L
$$
Integral transformation
Reference element integration: just change integration variable from \( x \) to \( X \). Introduce local basis function
$$
\refphi_r(X) = \basphi_{q(e,r)}(x(X))
$$
$$
\tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
= \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\underbrace{\frac{dx}{dX}}_{\det J = h/2}dX
= \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\det J\,dX
$$
$$
\tilde b^{(e)}_{r} = \int_{\Omega^{(e)}}f(x)\basphi_{q(e,r)}(x)dx
= \int\limits_{-1}^1 f(x(X))\refphi_r(X)\det J\,dX
$$
Advantages of the reference element
- Always the same domain for integration: \( [-1,1] \)
- We only need formulas for \( \refphi_r(X) \) over one element (no piecewise polynomial definition)
- \( \refphi_r(X) \) is the same for all elements: no dependence on element length and location, which is "factored out" in the mapping and \( \det J \)
Standardized basis functions for P1 elements
$$
\begin{align}
\refphi_0(X) &= \half (1 - X)
\tag{10}\\
\refphi_1(X) &= \half (1 + X)
\tag{11}
\end{align}
$$
Note: simple polynomial expressions (no need to consider piecewisely defined functions)
Standardized basis functions for P2 elements
$$
\begin{align}
\refphi_0(X) &= \half (X-1)X
\tag{12}\\
\refphi_1(X) &= 1 - X^2
\tag{13}\\
\refphi_2(X) &= \half (X+1)X
\tag{14}
\end{align}
$$
Easy to generalize to arbitrary order!
How to find the polynomial expressions?
Three alternatives:
- Map the global basis function \( \basphi_i(x) \) over an element to \( X \) coordinates
- Compute \( \refphi_r(X) \) from scratch using
- a given polynomial order \( d \)
- \( \refphi_r(X)=1 \) at local node 1
- \( \refphi_r(X)=1 \) at all other local nodes
Integration over a reference element; element matrix
P1 elements and \( f(x)=x(1-x) \).
$$
\begin{align}
\tilde A^{(e)}_{0,0}
&= \int_{-1}^1 \refphi_0(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1-X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X)^2 dX = \frac{h}{3}
\tag{15}\\
\tilde A^{(e)}_{1,0}
&= \int_{-1}^1 \refphi_1(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X^2) dX = \frac{h}{6}
\tag{16}\\
\tilde A^{(e)}_{0,1} &= \tilde A^{(e)}_{1,0}
\tag{17}\\
\tilde A^{(e)}_{1,1}
&= \int_{-1}^1 \refphi_1(X)\refphi_1(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1+X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1+X)^2 dX = \frac{h}{3}
\tag{18}
\end{align}
$$
Integration over a reference element; element vector
$$
\begin{align}
\tilde b^{(e)}_{0}
&= \int_{-1}^1 f(x(X))\refphi_0(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1-X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} + \frac{1}{6} h^{2} x_{m} - \frac{1}{12} h^{2} - \half h x_{m}^{2} + \half h x_{m}
\tag{19}\\
\tilde b^{(e)}_{1}
&= \int_{-1}^1 f(x(X))\refphi_1(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1+X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} - \frac{1}{6} h^{2} x_{m} + \frac{1}{12} h^{2} -
\half h x_{m}^{2} + \half h x_{m}
\tag{20}
\end{align}
$$
\( x_m \): element midpoint.
Tedious calculations! Let's use symbolic software
>>> import sympy as sym
>>> x, x_m, h, X = sym.symbols('x x_m h X')
>>> sym.integrate(h/8*(1-X)**2, (X, -1, 1))
h/3
>>> sym.integrate(h/8*(1+X)*(1-X), (X, -1, 1))
h/6
>>> x = x_m + h/2*X
>>> b_0 = sym.integrate(h/4*x*(1-x)*(1-X), (X, -1, 1))
>>> print b_0
-h**3/24 + h**2*x_m/6 - h**2/12 - h*x_m**2/2 + h*x_m/2
Can print out in LaTeX too (convenient for copying into reports):
>>> print sym.latex(b_0, mode='plain')
- \frac{1}{24} h^{3} + \frac{1}{6} h^{2} x_{m}
- \frac{1}{12} h^{2} - \half h x_{m}^{2}
+ \half h x_{m}
Implementation
- Coming functions appear in fe_approx1D.py
- Functions can operate in symbolic or numeric mode
- The code documents all steps in finite element calculations!
Compute finite element basis functions in the reference element
Let \( \refphi_r(X) \) be a Lagrange polynomial of degree d:
import sympy as sym
import numpy as np
def phi_r(r, X, d):
if isinstance(X, sym.Symbol):
h = sym.Rational(1, d) # node spacing
nodes = [2*i*h - 1 for i in range(d+1)]
else:
# assume X is numeric: use floats for nodes
nodes = np.linspace(-1, 1, d+1)
return Lagrange_polynomial(X, r, nodes)
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
def basis(d=1):
"""Return the complete basis."""
X = sym.Symbol('X')
phi = [phi_r(r, X, d) for r in range(d+1)]
return phi
Compute the element matrix
def element_matrix(phi, Omega_e, symbolic=True):
n = len(phi)
A_e = sym.zeros((n, n))
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
detJ = h/2 # dx/dX
for r in range(n):
for s in range(r, n):
A_e[r,s] = sym.integrate(phi[r]*phi[s]*detJ, (X, -1, 1))
A_e[s,r] = A_e[r,s]
return A_e
Example on symbolic vs numeric element matrix
>>> from fe_approx1D import *
>>> phi = basis(d=1)
>>> phi
[1/2 - X/2, 1/2 + X/2]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=True)
[h/3, h/6]
[h/6, h/3]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=False)
[0.0333333333333333, 0.0166666666666667]
[0.0166666666666667, 0.0333333333333333]
Compute the element vector
def element_vector(f, phi, Omega_e, symbolic=True):
n = len(phi)
b_e = sym.zeros((n, 1))
# Make f a function of X
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
x = (Omega_e[0] + Omega_e[1])/2 + h/2*X # mapping
f = f.subs('x', x) # substitute mapping formula for x
detJ = h/2 # dx/dX
for r in range(n):
b_e[r] = sym.integrate(f*phi[r]*detJ, (X, -1, 1))
return b_e
Note f.subs('x', x): replace x by \( x(X) \) such that f contains X
Fallback on numerical integration if symbolic integration of \( \int f\refphi_r dx \) fails
- Element matrix: only polynomials and
sympyalways succeeds - Element vector: \( \int f\refphi \dx \) can fail
(
sympythen returns anIntegralobject instead of a number)
def element_vector(f, phi, Omega_e, symbolic=True):
...
I = sym.integrate(f*phi[r]*detJ, (X, -1, 1)) # try...
if isinstance(I, sym.Integral):
h = Omega_e[1] - Omega_e[0] # Ensure h is numerical
detJ = h/2
integrand = sym.lambdify([X], f*phi[r]*detJ)
I = sym.mpmath.quad(integrand, [-1, 1])
b_e[r] = I
...
Linear system assembly and solution
def assemble(nodes, elements, phi, f, symbolic=True):
N_n, N_e = len(nodes), len(elements)
zeros = sym.zeros if symbolic else np.zeros
A = zeros((N_n, N_n))
b = zeros((N_n, 1))
for e in range(N_e):
Omega_e = [nodes[elements[e][0]], nodes[elements[e][-1]]]
A_e = element_matrix(phi, Omega_e, symbolic)
b_e = element_vector(f, phi, Omega_e, symbolic)
for r in range(len(elements[e])):
for s in range(len(elements[e])):
A[elements[e][r],elements[e][s]] += A_e[r,s]
b[elements[e][r]] += b_e[r]
return A, b
Linear system solution
if symbolic:
c = A.LUsolve(b) # sympy arrays, symbolic Gaussian elim.
else:
c = np.linalg.solve(A, b) # numpy arrays, numerical solve
Note: the symbolic computation of A, b and A.LUsolve(b)
can be very tedious.
Example on computing symbolic approximations
>>> h, x = sym.symbols('h x')
>>> nodes = [0, h, 2*h]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0]
[h/6, 2*h/3, h/6]
[ 0, h/6, h/3]
>>> b
[ h**2/6 - h**3/12]
[ h**2 - 7*h**3/6]
[5*h**2/6 - 17*h**3/12]
>>> c = A.LUsolve(b)
>>> c
[ h**2/6]
[12*(7*h**2/12 - 35*h**3/72)/(7*h)]
[ 7*(4*h**2/7 - 23*h**3/21)/(2*h)]
Example on computing numerical approximations
>>> nodes = [0, 0.5, 1]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> x = sym.Symbol('x')
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=False)
>>> A
[ 0.166666666666667, 0.0833333333333333, 0]
[0.0833333333333333, 0.333333333333333, 0.0833333333333333]
[ 0, 0.0833333333333333, 0.166666666666667]
>>> b
[ 0.03125]
[0.104166666666667]
[ 0.03125]
>>> c = A.LUsolve(b)
>>> c
[0.0416666666666666]
[ 0.291666666666667]
[0.0416666666666666]
The structure of the coefficient matrix
>>> d=1; N_e=8; Omega=[0,1] # 8 linear elements on [0,1]
>>> phi = basis(d)
>>> f = x*(1-x)
>>> nodes, elements = mesh_symbolic(N_e, d, Omega)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0, 0, 0, 0, 0, 0, 0]
[h/6, 2*h/3, h/6, 0, 0, 0, 0, 0, 0]
[ 0, h/6, 2*h/3, h/6, 0, 0, 0, 0, 0]
[ 0, 0, h/6, 2*h/3, h/6, 0, 0, 0, 0]
[ 0, 0, 0, h/6, 2*h/3, h/6, 0, 0, 0]
[ 0, 0, 0, 0, h/6, 2*h/3, h/6, 0, 0]
[ 0, 0, 0, 0, 0, h/6, 2*h/3, h/6, 0]
[ 0, 0, 0, 0, 0, 0, h/6, 2*h/3, h/6]
[ 0, 0, 0, 0, 0, 0, 0, h/6, h/3]
Note: do this by hand to understand what is going on!
General result: the coefficient matrix is sparse
- Sparse = most of the entries are zeros
- Below: P1 elements
$$
A = \frac{h}{6}
\left(
\begin{array}{cccccccccc}
2 & 1 & 0
&\cdots & \cdots & \cdots & \cdots & \cdots & 0 \\
1 & 4 & 1 & \ddots & & & & & \vdots \\
0 & 1 & 4 & 1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & 1 & 4 & 1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & 1 & 4 & 1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & 1 & 2
\end{array}
\right)
$$
Exemplifying the sparsity for P2 elements
$$
A = \frac{h}{30}
\left(
\begin{array}{ccccccccc}
4 & 2 & - 1 & 0
& 0 & 0 & 0 & 0 & 0\\
2 & 16 & 2
& 0 & 0 & 0 & 0 & 0 & 0\\- 1 & 2 &
8 & 2 & - 1 & 0 & 0 & 0 & 0\\
0 & 0 & 2 & 16 & 2 & 0 & 0 & 0 & 0\\
0 & 0 & - 1 & 2 & 8 & 2 & - 1 & 0 & 0\\
0 & 0 & 0 & 0 & 2 & 16 & 2 & 0 & 0\\
0 & 0 & 0 & 0 & - 1 & 2 & 8 & 2 & - 1
\\0 & 0 & 0 & 0 & 0 & 0 &
2 & 16 & 2\\0 & 0 & 0 & 0 & 0
& 0 & - 1 & 2 & 4
\end{array}
\right)
$$
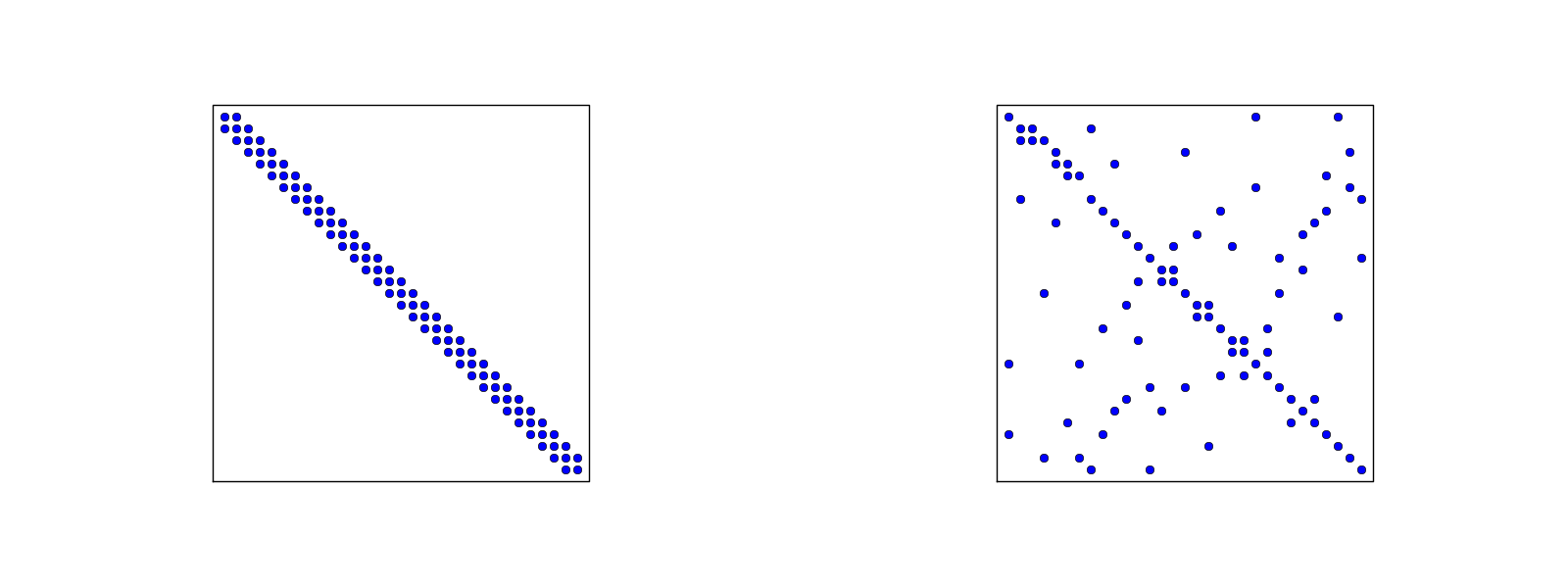
Matrix sparsity pattern for regular/random numbering of P1 elements
- Left: number nodes and elements from left to right
- Right: number nodes and elements arbitrarily
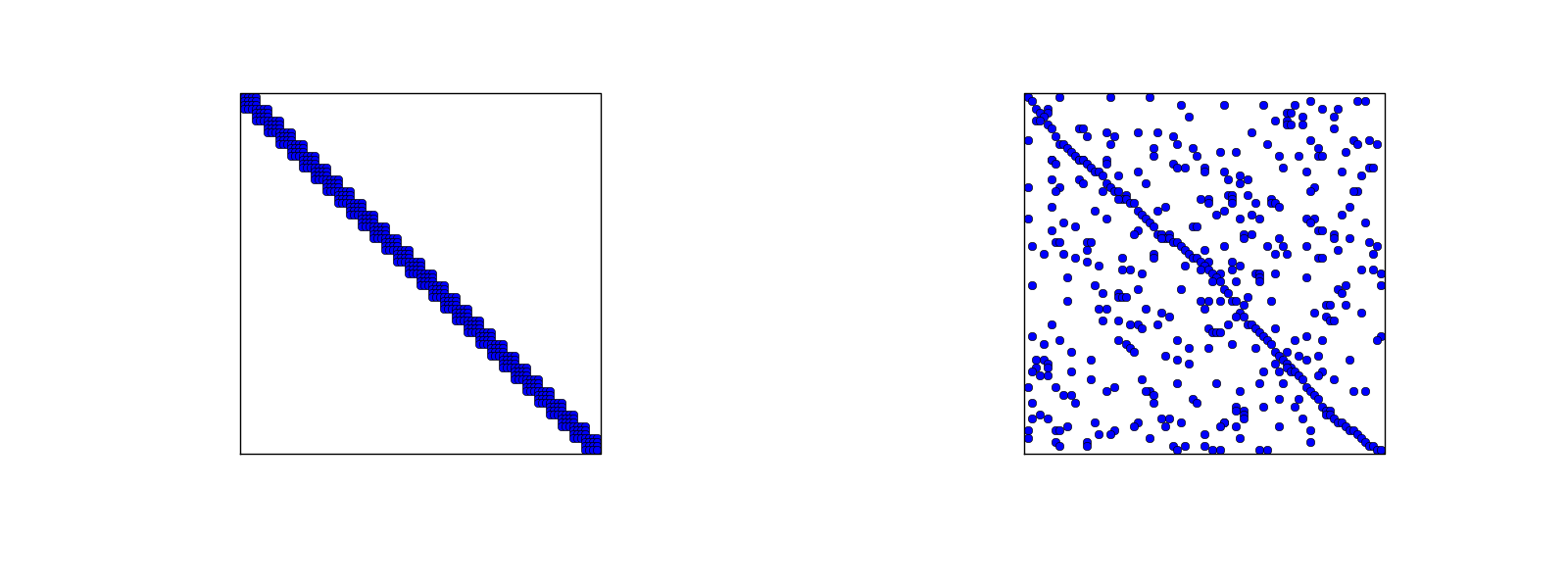
Matrix sparsity pattern for regular/random numbering of P3 elements
- Left: number nodes and elements from left to right
- Right: number nodes and elements arbitrarily
Sparse matrix storage and solution
The minimum storage requirements for the coefficient matrix \( A_{i,j} \):
- P1 elements: only 3 nonzero entries per row
- P2 elements: only 5 nonzero entries per row
- P3 elements: only 7 nonzero entries per row
- It is important to utilize sparse storage and sparse solvers
- In Python:
scipy.sparsepackage
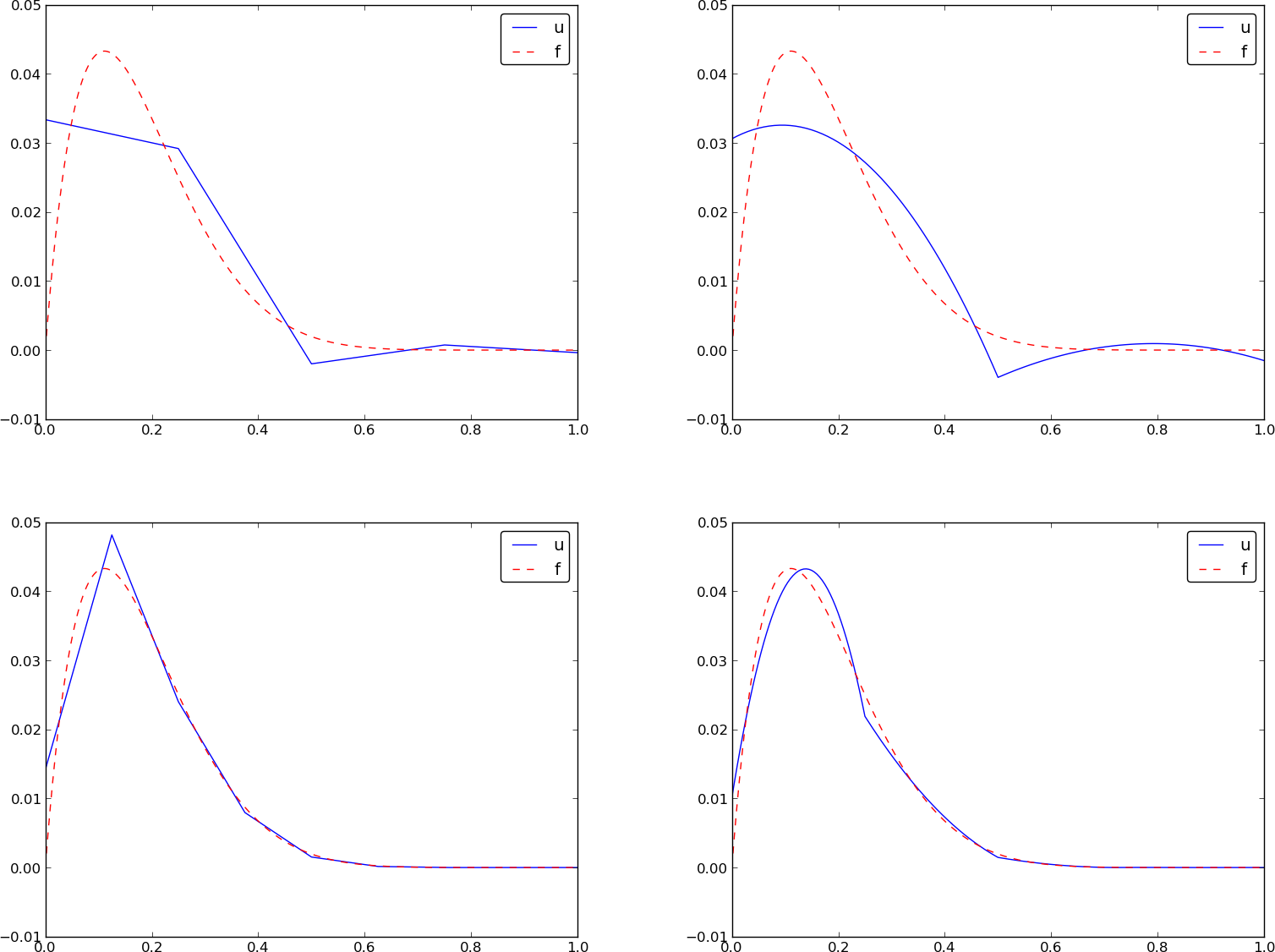
Approximate \( f\sim x^9 \) by various elements; code
Compute a mesh with \( N_e \) elements, basis functions of degree \( d \), and approximate a given symbolic expression \( f(x) \) by a finite element expansion \( u(x) = \sum_jc_j\basphi_j(x) \):
import sympy as sym
from fe_approx1D import approximate
x = sym.Symbol('x')
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=4)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=2)
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=8)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=4)
Approximate \( f\sim x^9 \) by various elements; plot
Comparison of finite element and finite difference approximation
- Finite difference approximation \( u_i \) of a function \( f(x) \): simply choose \( u_i = f(x_i) \)
- This is the same as \( u\approx\sum_i c_i\basphi_i \) + interpolation
(see next slide) - \( u\approx\sum_i c_i\basphi_i \) + Galerkin/projection or least squares method: must derive and solve a linear system
- What is really the difference in the approximation \( u \)?
Interpolation/collocation with finite elements
Let \( \{\xno{i}\}_{i\in\If} \) be the nodes in the mesh. Collocation/interpolation means
$$
u(\xno{i})=f(\xno{i}),\quad i\in\If,
$$
which translates to
$$ \sum_{j\in\If} c_j \basphi_j(\xno{i}) = f(\xno{i}),$$
but \( \basphi_j(\xno{i})=0 \) if \( i\neq j \) so the sum collapses to one
term \( c_i\basphi_i(\xno{i}) = c_i \), and we have the result
$$
c_i = f(\xno{i})
$$
Same result as the standard finite difference approach, but finite elements define \( u \) also between the \( \xno{i} \) points
Galerkin/project and least squares vs collocation/interpolation or finite differences
- Scope: work with P1 elements
- Use projection/Galerkin or least squares (equivalent)
- Interpret the resulting linear system as finite difference equations
The P1 finite element machinery results in a linear system where equation no \( i \) is
$$
\frac{h}{6}(u_{i-1} + 4u_i + u_{i+1}) = (f,\basphi_i)
$$
Note:
- We have used \( u_i \) for \( c_i \) to make notation similar to finite differences
- The finite difference counterpart is just \( u_i=f_i \)
Expressing the left-hand side in finite difference operator notation
Rewrite the left-hand side of finite element equation no \( i \):
$$
h(u_i + \frac{1}{6}(u_{i-1} - 2u_i + u_{i+1})) = [h(u + \frac{h^2}{6}D_x D_x u)]_i
$$
This is the standard finite difference approximation of
$$ h(u + \frac{h^2}{6}u'')$$
Treating the right-hand side; Trapezoidal rule
$$ (f,\basphi_i) = \int_{\xno{i-1}}^{\xno{i}} f(x)\frac{1}{h} (x - \xno{i-1}) dx
+ \int_{\xno{i}}^{\xno{i+1}} f(x)\frac{1}{h}(1 - (x - x_{i})) dx
$$
Cannot do much unless we specialize \( f \) or use numerical integration.
Trapezoidal rule using the nodes:
$$ (f,\basphi_i) = \int_\Omega f\basphi_i dx\approx h\half(
f(\xno{0})\basphi_i(\xno{0}) + f(\xno{N})\basphi_i(\xno{N}))
+ h\sum_{j=1}^{N-1} f(\xno{j})\basphi_i(\xno{j})
$$
\( \basphi_i(\xno{j})=\delta_{ij} \), so this formula collapses to one term:
$$
(f,\basphi_i) \approx hf(\xno{i}),\quad i=1,\ldots,N-1\thinspace.
$$
Same result as in collocation (interpolation) and the finite difference method!
Treating the right-hand side; Simpson's rule
$$ \int_\Omega g(x)dx \approx \frac{h}{6}\left( g(\xno{0}) +
2\sum_{j=1}^{N-1} g(\xno{j})
+ 4\sum_{j=0}^{N-1} g(\xno{j+\half}) + f(\xno{2N})\right),
$$
Our case: \( g=f\basphi_i \). The sums collapse because \( \basphi_i=0 \) at most of
the points.
$$
(f,\basphi_i) \approx \frac{h}{3}(f_{i-\half} + f_i + f_{i+\half})
$$
Conclusions:
- While the finite difference method just samples \( f \) at \( x_i \), the finite element method applies an average (smoothing) of \( f \) around \( x_i \)
- On the left-hand side we have a term \( \sim hu'' \), and \( u'' \) also contribute to smoothing
- There is some inherent smoothing in the finite element method
Finite element approximation vs finite differences
With Trapezoidal integration of \( (f,\basphi_i) \), the finite element method essentially solve
$$
u + \frac{h^2}{6} u'' = f,\quad u'(0)=u'(L)=0,
$$
by the finite difference method
$$
[u + \frac{h^2}{6} D_x D_x u = f]_i
$$
With Simpson integration of \( (f,\basphi_i) \) we essentially solve
$$
[u + \frac{h^2}{6} D_x D_x u = \bar f]_i,
$$
where
$$ \bar f_i = \frac{1}{3}(f_{i-1/2} + f_i + f_{i+1/2}) $$
Note: as \( h\rightarrow 0 \), \( hu''\rightarrow 0 \) and \( \bar f_i\rightarrow f_i \).
Making finite elements behave as finite differences
- Can we adjust the finite element method so that we do not get the extra \( hu'' \) smoothing term and averaging of \( f \)?
- This allows finite elements to inherit (desired) properties of finite differences
Result:
- Compute all integrals by the Trapezoidal method and P1 elements
- Specifically, the coefficient matrix becomes diagonal ("lumped") - no linear system (!)
- Loss of accuracy? The Trapezoidal rule has error \( \Oof{h^2} \), the same as the approximation error in P1 elements
Limitations of the nodes and element concepts
So far,
- Nodes: points for defining \( \basphi_i \) and computing \( u \) values
- Elements: subdomain (containing a few nodes)
- This is a common notion of nodes and elements
One problem:
- Our algorithms need nodes at the element boundaries
- This is often not desirable, so we need to throw the
nodesandelementsarrays away and find a more generalized element concept
The generalized element concept has cells, vertices, nodes, and degrees of freedom
- We introduce cell for the subdomain that we up to now called element
- A cell has vertices (interval end points)
- Nodes are, almost as before, points where we want to compute unknown functions
- Degrees of freedom is what the \( c_j \) represent (usually function values at nodes)
The concept of a finite element
- a reference cell in a local reference coordinate system
- a set of basis functions \( \refphi_r \) defined on the cell
- a set of degrees of freedom (e.g., function values) that uniquely determine the basis functions such that \( \refphi_r=1 \) for degree of freedom number \( r \) and \( \refphi_r=0 \) for all other degrees of freedom
- a mapping between local and global degree of freedom numbers (dof map)
- a geometric mapping of the reference cell onto to cell in the physical domain: \( [-1,1]\ \Rightarrow\ [x_L,x_R] \)
Basic data structures: vertices, cells, dof_map
- Cell vertex coordinates:
vertices(equalsnodesfor P1 elements) - Element vertices:
cells[e][r]holds global vertex number of local vertex norin elemente(same aselementsfor P1 elements) -
dof_map[e,r]maps local dofrin elementeto global dof number (same aselementsfor Pd elements)
The assembly process now applies dof_map:
A[dof_map[e][r], dof_map[e][s]] += A_e[r,s]
b[dof_map[e][r]] += b_e[r]
Example: data structures for P2 elements

vertices = [0, 0.4, 1]
cells = [[0, 1], [1, 2]]
dof_map = [[0, 1, 2], [2, 3, 4]]
Example: P0 elements
Example: Same mesh, but \( u \) is piecewise constant in each cell (P0 element).
Same vertices and cells, but
dof_map = [[0], [1]]
May think of one node in the middle of each element.
We will hereafter work with cells, vertices, and dof_map.
A program with the fundamental algorithmic steps
# Use modified fe_approx1D module
from fe_approx1D_numint import *
x = sym.Symbol('x')
f = x*(1 - x)
N_e = 10
# Create mesh with P3 (cubic) elements
vertices, cells, dof_map = mesh_uniform(N_e, d=3, Omega=[0,1])
# Create basis functions on the mesh
phi = [basis(len(dof_map[e])-1) for e in range(N_e)]
# Create linear system and solve it
A, b = assemble(vertices, cells, dof_map, phi, f)
c = np.linalg.solve(A, b)
# Make very fine mesh and sample u(x) on this mesh for plotting
x_u, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=51)
plot(x_u, u)
Approximating a parabola by P0 elements
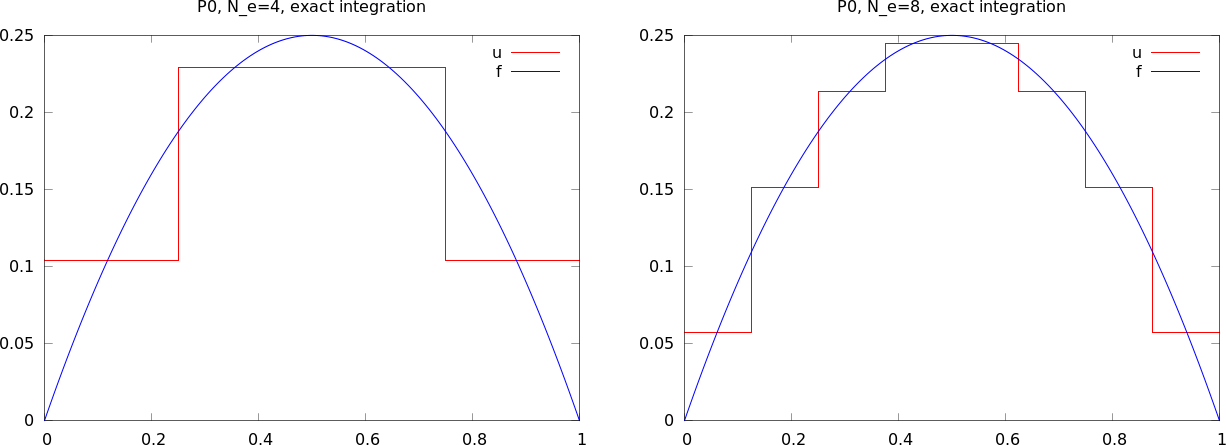
The approximate function automates the steps in the previous slide:
from fe_approx1D_numint import *
x=sym.Symbol("x")
for N_e in 4, 8:
approximate(x*(1-x), d=0, N_e=N_e, Omega=[0,1])
Computing the error of the approximation; principles
$$ L^2 \hbox{ error: }\quad ||e||_{L^2} =
\left(\int_{\Omega} e^2 dx\right)^{1/2}$$
Accurate approximation of the integral:
- Sample \( u(x) \) at many points in each element (call
u_glob, returnsxandu) - Use the Trapezoidal rule based on the samples
- It is important to integrate \( u \) accurately over the elements
- (In a finite difference method we would just sample the mesh point values)
Computing the error of the approximation; details
We need a version of the Trapezoidal rule valid for non-uniformly spaced points:
$$ \int_\Omega g(x) dx \approx \sum_{j=0}^{n-1} \half(g(x_j) +
g(x_{j+1}))(x_{j+1}-x_j)$$
# Given c, compute x and u values on a very fine mesh
x, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=101)
# Compute the error on the very fine mesh
e = f(x) - u
e2 = e**2
# Vectorized Trapezoidal rule
E = np.sqrt(0.5*np.sum((e2[:-1] + e2[1:])*(x[1:] - x[:-1]))
How does the error depend on \( h \) and \( d \)?
Theory and experiments show that the least squares or projection/Galerkin method in combination with Pd elements of equal length \( h \) has an error
$$
||e||_{L^2} = Ch^{d+1}
$$
where \( C \) depends on \( f \), but not on \( h \) or \( d \).
Cubic Hermite polynomials; definition
- Can we construct \( \basphi_i(x) \) with continuous derivatives? Yes!
Consider a reference cell \( [-1,1] \). We introduce two nodes, \( X=-1 \) and \( X=1 \). The degrees of freedom are
- 0: value of function at \( X=-1 \)
- 1: value of first derivative at \( X=-1 \)
- 2: value of function at \( X=1 \)
- 3: value of first derivative at \( X=1 \)
Derivatives as unknowns ensure the same \( \basphi_i'(x) \) value at nodes and thereby continuous derivatives.
Cubic Hermite polynomials; derivation
4 constraints on \( \refphi_r \) (1 for dof \( r \), 0 for all others):
- \( \refphi_0(\Xno{0}) = 1 \), \( \refphi_0(\Xno{1}) = 0 \), \( \refphi_0'(\Xno{0}) = 0 \), \( \refphi_0'(\Xno{1}) = 0 \)
- \( \refphi_1'(\Xno{0}) = 1 \), \( \refphi_1'(\Xno{1}) = 0 \), \( \refphi_1(\Xno{0}) = 0 \), \( \refphi_1(\Xno{1}) = 0 \)
- \( \refphi_2(\Xno{1}) = 1 \), \( \refphi_2(\Xno{0}) = 0 \), \( \refphi_2'(\Xno{0}) = 0 \), \( \refphi_2'(\Xno{1}) = 0 \)
- \( \refphi_3'(\Xno{1}) = 1 \), \( \refphi_3'(\Xno{0}) = 0 \), \( \refphi_3(\Xno{0}) = 0 \), \( \refphi_3(\Xno{1}) = 0 \)
This gives 4 linear, coupled equations for each \( \refphi_r \) to determine the 4 coefficients in the cubic polynomial
Cubic Hermite polynomials; result
$$
\begin{align}
\refphi_0(X) &= 1 - \frac{3}{4}(X+1)^2 + \frac{1}{4}(X+1)^3
\tag{21}\\
\refphi_1(X) &= -(X+1)(1 - \half(X+1))^2
\tag{22}\\
\refphi_2(X) &= \frac{3}{4}(X+1)^2 - \half(X+1)^3
\tag{23}\\
\refphi_3(X) &= -\half(X+1)(\half(X+1)^2 - (X+1))
\tag{24}\\
\tag{25}
\end{align}
$$
Numerical integration
- \( \int_\Omega f\basphi_idx \) must in general be computed by numerical integration
- Numerical integration is often used for the matrix too
Common form of a numerical integration rule
$$
\int_{-1}^{1} g(X)dX \approx \sum_{j=0}^M w_jg(\bar X_j),
$$
where
- \( \bar X_j \) are integration points
- \( w_j \) are integration weights
Different rules correspond to different choices of points and weights
The Midpoint rule
Simplest possibility: the Midpoint rule,
$$
\int_{-1}^{1} g(X)dX \approx 2g(0),\quad \bar X_0=0,\ w_0=2,
$$
Exact for linear integrands
Newton-Cotes rules apply the nodes
- Idea: use a fixed, uniformly distributed set of points in \( [-1,1] \)
- The points often coincides with nodes
- Very useful for making \( \basphi_i\basphi_j=0 \) and get diagonal ("mass") matrices ("lumping")
The Trapezoidal rule:
$$
\int_{-1}^{1} g(X)dX \approx g(-1) + g(1),\quad \bar X_0=-1,\ \bar X_1=1,\ w_0=w_1=1,
$$
Simpson's rule:
$$
\int_{-1}^{1} g(X)dX \approx \frac{1}{3}\left(g(-1) + 4g(0)
+ g(1)\right),
$$
where
$$
\bar X_0=-1,\ \bar X_1=0,\ \bar X_2=1,\ w_0=w_2=\frac{1}{3},\ w_1=\frac{4}{3}
$$
Gauss-Legendre rules apply optimized points
- Optimize the location of points to get higher accuracy
- Gauss-Legendre rules (quadrature) adjust points and weights to integrate polynomials exactly
$$
\begin{align}
M=1&:\quad \bar X_0=-\frac{1}{\sqrt{3}},\
\bar X_1=\frac{1}{\sqrt{3}},\ w_0=w_1=1
\tag{26}\\
M=2&:\quad \bar X_0=-\sqrt{\frac{3}{{5}}},\ \bar X_0=0,\
\bar X_2= \sqrt{\frac{3}{{5}}},\ w_0=w_2=\frac{5}{9},\ w_1=\frac{8}{9}
\tag{27}
\end{align}
$$
- \( M=1 \): integrates 3rd degree polynomials exactly
- \( M=2 \): integrates 5th degree polynomials exactly
- In general, \( M \)-point rule integrates a polynomial of degree \( 2M+1 \) exactly.
See numint.py for a large collection of Gauss-Legendre rules.
Approximation of functions in 2D
All the concepts and algorithms developed for approximation of 1D functions \( f(x) \) can readily be extended to 2D functions \( f(x,y) \) and 3D functions \( f(x,y,z) \). Key formulas stay the same.
Quick overview of the 2D case
Inner product in 2D:
$$
(f,g) = \int_\Omega f(x,y)g(x,y) dx dy
$$
Least squares and project/Galerkin lead to a linear system
$$
\begin{align*}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If\\
A_{i,j} &= (\baspsi_i,\baspsi_j)\\
b_i &= (f,\baspsi_i)
\end{align*}
$$
Challenge: How to construct 2D basis functions \( \baspsi_i(x,y) \)?
2D basis functions as tensor products of 1D functions
Use a 1D basis for \( x \) variation and a similar for \( y \) variation:
$$
\begin{align}
V_x &= \mbox{span}\{ \hat\baspsi_0(x),\ldots,\hat\baspsi_{N_x}(x)\}
\tag{28}\\
V_y &= \mbox{span}\{ \hat\baspsi_0(y),\ldots,\hat\baspsi_{N_y}(y)\}
\tag{29}
\end{align}
$$
The 2D vector space can be defined as a tensor product \( V = V_x\otimes V_y \) with basis functions
$$
\baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y)
\quad p\in\Ix,q\in\Iy\tp
$$
Tensor products
Given two vectors \( a=(a_0,\ldots,a_M) \) and \( b=(b_0,\ldots,b_N) \) their outer tensor product, also called the dyadic product, is \( p=a\otimes b \), defined through
$$ p_{i,j}=a_ib_j,\quad i=0,\ldots,M,\ j=0,\ldots,N\tp$$
Note: \( p \) has two indices (as a matrix or two-dimensional array)
Example: 2D basis as tensor product of 1D spaces,
$$ \baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad p\in\Ix,q\in\Iy$$
Double or single index?
The 2D basis can employ a double index and double sum:
$$ u = \sum_{p\in\Ix}\sum_{q\in\Iy} c_{p,q}\baspsi_{p,q}(x,y)
$$
Or just a single index:
$$ u = \sum_{j\in\If} c_j\baspsi_j(x,y)$$
with an index mapping \( (p,q)\rightarrow i \):
$$
\baspsi_i(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad i=p (N_y+1) + q\hbox{ or } i=q (N_x+1) + p
$$
Example on 2D (bilinear) basis functions; formulas
In 1D we use the basis
$$ \{ 1, x \} $$
2D tensor product (all combinations):
$$ \baspsi_{0,0}=1,\quad \baspsi_{1,0}=x, \quad \baspsi_{0,1}=y,
\quad \baspsi_{1,1}=xy
$$
or with a single index:
$$ \baspsi_0=1,\quad \baspsi_1=x, \quad \baspsi_2=y,\quad\baspsi_3 =xy
$$
See notes for details of a hand-calculation.
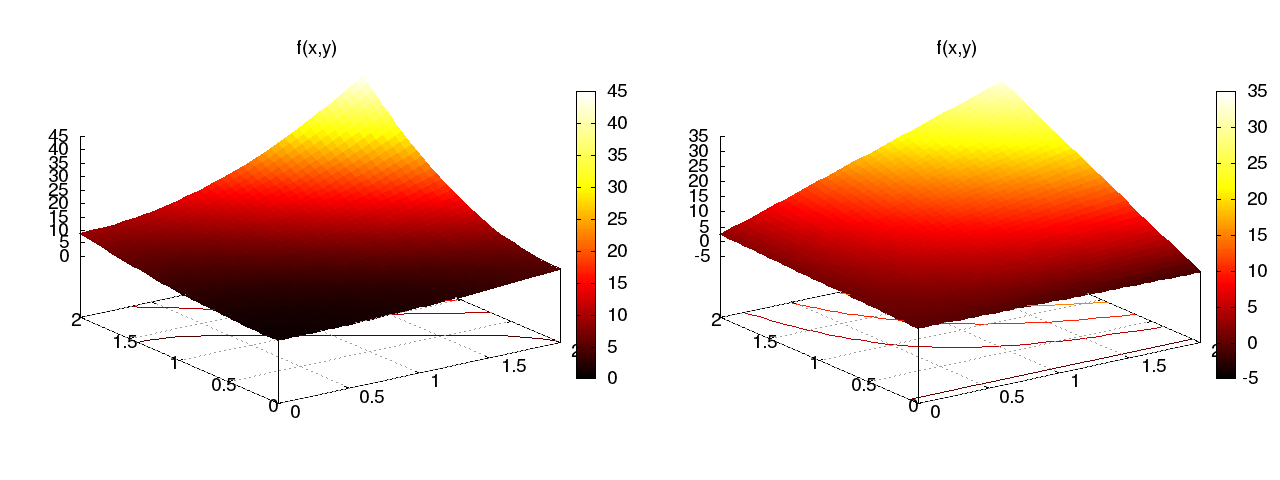
Example on 2D (bilinear) basis functions; plot
Quadratic \( f(x,y) = (1+x^2)(1+2y^2) \) (left), bilinear \( u \) (right):
Implementation; principal changes to the 1D code
Very small modification of approx1D.py:
-
Omega = [[0, L_x], [0, L_y]] - Symbolic integration in 2D
- Construction of 2D (tensor product) basis functions
Implementation; 2D integration
import sympy as sym
integrand = psi[i]*psi[j]
I = sym.integrate(integrand,
(x, Omega[0][0], Omega[0][1]),
(y, Omega[1][0], Omega[1][1]))
# Fall back on numerical integration if symbolic integration
# was unsuccessful
if isinstance(I, sym.Integral):
integrand = sym.lambdify([x,y], integrand)
I = sym.mpmath.quad(integrand,
[Omega[0][0], Omega[0][1]],
[Omega[1][0], Omega[1][1]])
Implementation; 2D basis functions
Tensor product of 1D "Taylor-style" polynomials \( x^i \):
def taylor(x, y, Nx, Ny):
return [x**i*y**j for i in range(Nx+1) for j in range(Ny+1)]
Tensor product of 1D sine functions \( \sin((i+1)\pi x) \):
def sines(x, y, Nx, Ny):
return [sym.sin(sym.pi*(i+1)*x)*sym.sin(sym.pi*(j+1)*y)
for i in range(Nx+1) for j in range(Ny+1)]
Complete code in approx2D.py
Implementation; application
\( f(x,y) = (1+x^2)(1+2y^2) \)
>>> from approx2D import *
>>> f = (1+x**2)*(1+2*y**2)
>>> psi = taylor(x, y, 1, 1)
>>> Omega = [[0, 2], [0, 2]]
>>> u, c = least_squares(f, psi, Omega)
>>> print u
8*x*y - 2*x/3 + 4*y/3 - 1/9
>>> print sym.expand(f)
2*x**2*y**2 + x**2 + 2*y**2 + 1
Implementation; trying a perfect expansion
Add higher powers to the basis such that \( f\in V \):
>>> psi = taylor(x, y, 2, 2)
>>> u, c = least_squares(f, psi, Omega)
>>> print u
2*x**2*y**2 + x**2 + 2*y**2 + 1
>>> print u-f
0
Expected: \( u=f \) when \( f\in V \)
Generalization to 3D
Key idea:
$$ V = V_x\otimes V_y\otimes V_z$$
$$
\begin{align*}
a^{(q)} &= (a^{(q)}_0,\ldots,a^{(q)}_{N_q}),\quad q=0,\ldots,m\\
p &= a^{(0)}\otimes\cdots\otimes a^{(m)}\\
p_{i_0,i_1,\ldots,i_m} &= a^{(0)}_{i_1}a^{(1)}_{i_1}\cdots a^{(m)}_{i_m}
\end{align*}
$$
$$
\begin{align*}
\baspsi_{p,q,r}(x,y,z) &= \hat\baspsi_p(x)\hat\baspsi_q(y)\hat\baspsi_r(z)\\
u(x,y,z) &= \sum_{p\in\Ix}\sum_{q\in\Iy}\sum_{r\in\Iz} c_{p,q,r}
\baspsi_{p,q,r}(x,y,z)
\end{align*}
$$
Finite elements in 2D and 3D
The two great advantages of the finite element method:
- Can handle complex-shaped domains in 2D and 3D
- Can easily provide higher-order polynomials in the approximation
Finite elements in 1D: mostly for learning, insight, debugging
Examples on cell types
2D:
- triangles
- quadrilaterals
3D:
- tetrahedra
- hexahedra
Rectangular domain with 2D P1 elements
Deformed geometry with 2D P1 elements
Rectangular domain with 2D Q1 elements
Basis functions over triangles in the physical domain
The P1 triangular 2D element: \( u \) is linear \( ax + by + c \) over each triangular cell

Basic features of 2D elements
- Cells = triangles
- Vertices = corners of the cells
- Nodes = vertices
- Degrees of freedom = function values at the nodes
Linear mapping of reference element onto general triangular cell

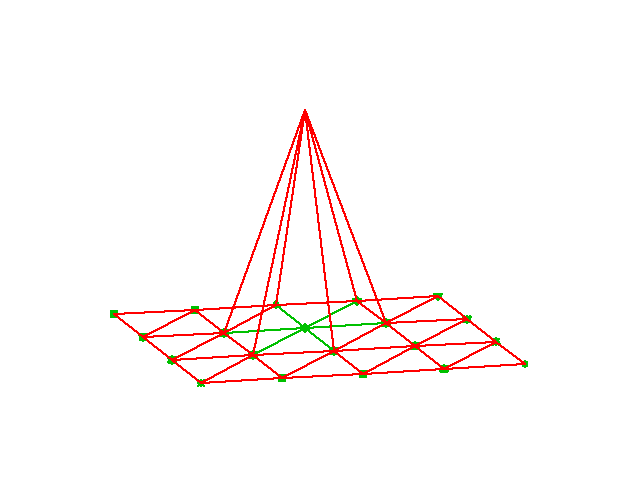
\( \basphi_i \): pyramid shape, composed of planes
- \( \basphi_i(x,y) \) varies linearly over each cell
- \( \basphi_i=1 \) at vertex (node) \( i \), 0 at all other vertices (nodes)
Element matrices and vectors
- As in 1D, the contribution from one cell to the matrix involves just a few entries, collected in the element matrix and vector
- \( \basphi_i\basphi_j\neq 0 \) only if \( i \) and \( j \) are degrees of freedom (vertices/nodes) in the same element
- The 2D P1 element has a \( 3\times 3 \) element matrix
Basis functions over triangles in the reference cell

$$
\begin{align}
\refphi_0(X,Y) &= 1 - X - Y
\tag{30}\\
\refphi_1(X,Y) &= X
\tag{31}\\
\refphi_2(X,Y) &= Y
\tag{32}
\end{align}
$$
Higher-degree \( \refphi_r \) introduce more nodes (dof = node values)
2D P1, P2, P3, P4, P5, and P6 elements

P1 elements in 1D, 2D, and 3D

P2 elements in 1D, 2D, and 3D

- Interval, triangle, tetrahedron: simplex element (plural quick-form: simplices)
- Side of the cell is called face
- Thetrahedron has also edges
Affine mapping of the reference cell; formula
Mapping of local \( \X = (X,Y) \) coordinates in the reference cell to global, physical \( \x = (x,y) \) coordinates:
$$
\begin{equation}
\x = \sum_{r} \refphi_r^{(1)}(\X)\xdno{q(e,r)}
\tag{33}
\end{equation}
$$
where
- \( r \) runs over the local vertex numbers in the cell
- \( \xdno{i} \) are the \( (x,y) \) coordinates of vertex \( i \)
- \( \refphi_r^{(1)} \) are P1 basis functions
This mapping preserves the straight/planar faces and edges.
Affine mapping of the reference cell; figure

Isoparametric mapping of the reference cell
Idea: Use the basis functions of the element (not only the P1 functions) to map the element
$$
\x = \sum_{r} \refphi_r(\X)\xdno{q(e,r)}
$$
Advantage: higher-order polynomial basis functions now map the reference cell to a curved triangle or tetrahedron.

Computing integrals
Integrals must be transformed from \( \Omega^{(e)} \) (physical cell) to \( \tilde\Omega^r \) (reference cell):
$$
\begin{align}
\int_{\Omega^{(e)}}\basphi_i (\x) \basphi_j (\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) \refphi_j (\X)
\det J\, \dX
\tag{34}\\
\int_{\Omega^{(e)}}\basphi_i (\x) f(\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) f(\x(\X)) \det J\, \dX
\tag{35}
\end{align}
$$
where \( \dx = dx dy \) or \( \dx = dxdydz \) and \( \det J \) is the determinant of the
Jacobian of the mapping \( \x(\X) \).
$$
J = \left[\begin{array}{cc}
\frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y}\\
\frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y}
\end{array}\right], \quad
\det J = \frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}
- \frac{\partial x}{\partial Y}\frac{\partial y}{\partial X}
$$
Affine mapping (33): \( \det J=2\Delta \), \( \Delta = \hbox{cell volume} \)
Remark on going from 1D to 2D/3D
Finite elements in 2D and 3D builds on the same ideas and concepts as in 1D, but there is simply much more to compute because the specific mathematical formulas in 2D and 3D are more complicated and the book keeping with dof maps also gets more complicated. The manual work is tedious, lengthy, and error-prone so automation by the computer is a must.