Finite elements can handle complex geometry, adaptive meshes, higher-order approximations and has a firm theory


The finite element method has many concepts and a jungle of details. This learning strategy minimizes the mixing of ideas, concepts, and technical details.
General idea of finding an approximation \( u(x) \) to some given \( f(x) \):
$$ u(x) = \sum_{i=0}^N c_i\baspsi_i(x) $$
where
We shall address three approaches:
Our mathematical framework for doing this is phrased in a way such that it becomes easy to understand and use the FEniCS software package for finite element computing.
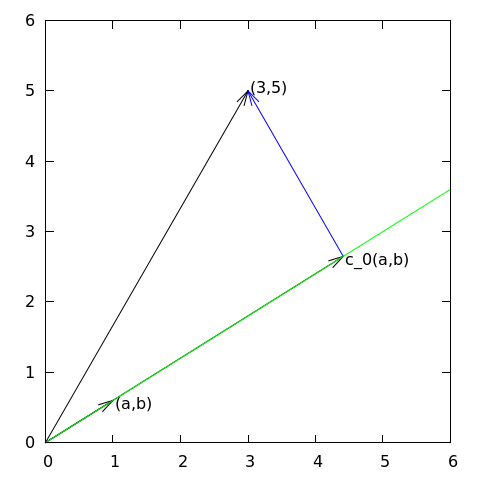
Given a vector \( \f = (3,5) \), find an approximation to \( \f \) directed along a given line.

$$ V = \mbox{span}\,\{ \psib_0\} $$
Define
$$
\begin{equation*}
\frac{\partial E}{\partial c_0} = 0
\end{equation*}
$$
$$
\begin{align*}
E(c_0) &= (\e,\e) = (\f - \u, \f - \u) = (\f - c_0\psib_0, \f - c_0\psib_0)\\
&= (\f,\f) - 2c_0(\f,\psib_0) + c_0^2(\psib_0,\psib_0)
\end{align*}
$$
$$
\begin{equation}
\frac{\partial E}{\partial c_0} = -2(\f,\psib_0) + 2c_0 (\psib_0,\psib_0) = 0
\tag{1}
\end{equation}
$$
$$
c_0 = \frac{(\f,\psib_0)}{(\psib_0,\psib_0)} = \frac{3a + 5b}{a^2 + b^2}
$$
Observation to be used later: the vanishing derivative (1) can be alternatively written as
$$ (\e, \psib_0) = 0 $$
Given a vector \( \f \), find an approximation \( \u\in V \):
$$
\begin{equation*}
V = \hbox{span}\,\{\psib_0,\ldots,\psib_N\}
\end{equation*}
$$
We have a set of linearly independent basis vectors \( \psib_0,\ldots,\psib_N \). Any \( \u\in V \) can then be written as
$$ \u = \sum_{j=0}^Nc_j\psib_j$$
Idea: find \( c_0,\ldots,c_N \) such that \( E= ||\e||^2 \) is minimized, \( \e=\f-\u \).
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (\e,\e) = (\f -\sum_jc_j\psib_j,\f -\sum_jc_j\psib_j)
\nonumber\\
&= (\f,\f) - 2\sum_{j=0}^Nc_j(\f,\psib_j) +
\sum_{p=0}^N\sum_{q=0}^N c_pc_q(\psib_p,\psib_q)
\end{align*}
$$
$$
\begin{equation*}
\frac{\partial E}{\partial c_i} = 0,\quad i=0,\ldots,N
\end{equation*}
$$
After some work we end up with a linear system
$$
\begin{align}
\sum_{j=0}^N A_{i,j}c_j &= b_i,\quad i=0,\ldots,N
\tag{2}\\
A_{i,j} &= (\psib_i,\psib_j)
\tag{3}\\
b_i &= (\psib_i, \f)
\tag{4}
\end{align}
$$
Can be shown that minimizing \( ||\e|| \) implies that \( \e \) is orthogonal to all \( \v\in V \):
$$
(\e,\v)=0,\quad \forall\v\in V
$$
which implies that \( \e \) most be orthogonal to each basis vector:
$$ (\e,\psib_i)=0,\quad i=0,\ldots,N $$
This orthogonality condition is the principle of the projection (or Galerkin) method. Leads to the same linear system as in the least squares method.
Let \( V \) be a function space spanned by a set of basis functions \( \baspsi_0,\ldots,\baspsi_N \),
$$
\begin{equation*}
V = \hbox{span}\,\{\baspsi_0,\ldots,\baspsi_N\}
\end{equation*}
$$
Find \( u\in V \) as a linear combination of the basis functions:
$$ u = \sum_{j\in\If} c_j\baspsi_j,\quad\If = \{0,1,\ldots,N\} $$
As in the vector case, minimize the (square) norm of the error, \( E \), with respect to the coefficients \( c_j \), \( j\in\If \):
$$
E = (e,e) = (f-u,f-u) = \left(f(x)-\sum_{j\in\If} c_j\baspsi_j(x), f(x)-\sum_{j\in\If} c_j\baspsi_j(x)\right)
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
But what is the scalar product when \( \baspsi_i \) is a function?
$$(f,g) = \int_\Omega f(x)g(x)\, dx$$
(natural extension from Eucledian product \( (\u, \v) = \sum_j u_jv_j \))
$$
\begin{align*}
E(c_0,\ldots,c_N) &= (e,e) = (f-u,f-u) \\
&= (f,f) -2\sum_{j\in\If} c_j(f,\baspsi_i)
+ \sum_{p\in\If}\sum_{q\in\If} c_pc_q(\baspsi_p,\baspsi_q)
\end{align*}
$$
$$ \frac{\partial E}{\partial c_i} = 0,\quad i=\in\If $$
The computations are identical to the vector case, and consequently we get a linear system
$$
\sum_{j\in\If} A_{i,j}c_j = b_i,\ i\in\If,\quad
A_{i,j} = (\baspsi_i,\baspsi_j),\
b_i = (f,\baspsi_i)
$$
As before, minimizing \( (e,e) \) is equivalent to
$$
(e,\baspsi_i)=0,\quad i\in\If
\tag{5}
$$
which is equivalent to
$$
(e,v)=0,\quad\forall v\in V
\tag{6}
$$
which is the projection (or Galerkin) method.
The algebra is the same as in the multi-dimensional vector case, and we get the same linear system as arose from the least squares method.
Approximate a parabola \( f(x) = 10(x-1)^2 - 1 \) by a straight line.
$$
\begin{equation*} V = \hbox{span}\,\{1, x\} \end{equation*}
$$
That is, \( \baspsi_0(x)=1 \), \( \baspsi_1(x)=x \), and \( N=1 \).
We seek
$$
\begin{equation*}
u=c_0\baspsi_0(x) + c_1\baspsi_1(x) = c_0 + c_1x
\end{equation*}
$$
$$
\begin{align*}
A_{0,0} &= (\baspsi_0,\baspsi_0) = \int_1^21\cdot 1\, dx = 1\\
A_{0,1} &= (\baspsi_0,\baspsi_1) = \int_1^2 1\cdot x\, dx = 3/2\\
A_{1,0} &= A_{0,1} = 3/2\\
A_{1,1} &= (\baspsi_1,\baspsi_1) = \int_1^2 x\cdot x\,dx = 7/3\\
b_1 &= (f,\baspsi_0) = \int_1^2 (10(x-1)^2 - 1)\cdot 1 \, dx = 7/3\\
b_2 &= (f,\baspsi_1) = \int_1^2 (10(x-1)^2 - 1)\cdot x\, dx = 13/3
\end{align*}
$$
Solution of 2x2 linear system:
$$ c_0 = -38/3,\quad c_1 = 10,\quad u(x) = 10x - \frac{38}{3} $$
Consider symbolic computation of the linear system, where
sympy expression f (involving
the symbol x),psi is a list of \( \sequencei{\baspsi} \),Omega is a 2-tuple/list holding the domain \( \Omega \)Carry out the integrations, solve the linear system, and return \( u(x)=\sum_jc_j\baspsi_j(x) \)
import sympy as sym
def least_squares(f, psi, Omega):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
for i in range(N+1):
for j in range(i, N+1):
A[i,j] = sym.integrate(psi[i]*psi[j],
(x, Omega[0], Omega[1]))
A[j,i] = A[i,j]
b[i,0] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i]
return u, c
Observe: symmetric coefficient matrix so we can halve the integrations.
sym.integrate fails, it returns an sym.Integral object.
We can test on this object and fall back on numerical integration.symbolic to explicitly choose
between symbolic and numerical computing.
def least_squares(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
for j in range(i, N+1):
integrand = psi[i]*psi[j]
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
# Could not integrate symbolically,
# fall back on numerical integration
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
A[i,j] = A[j,i] = I
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i,0] = I
...
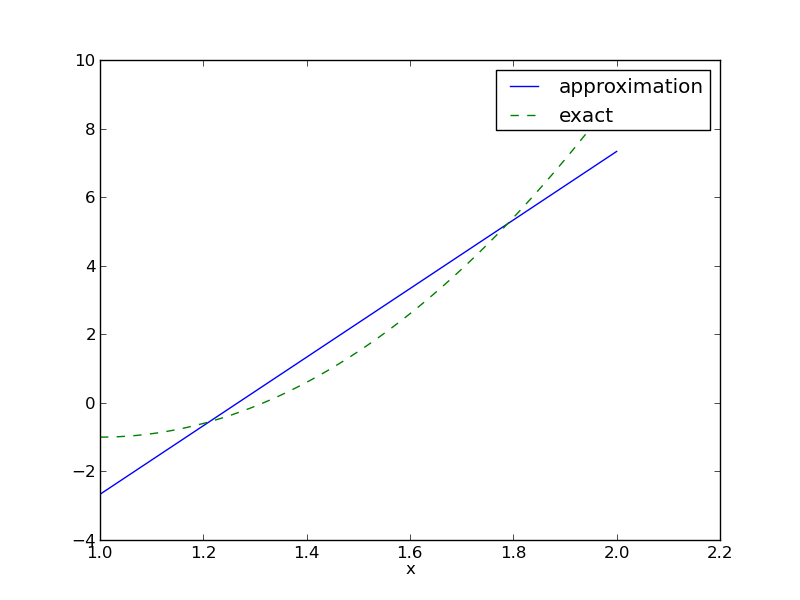
Compare \( f \) and \( u \) visually:
def comparison_plot(f, u, Omega, filename='tmp.pdf'):
x = sym.Symbol('x')
# Turn f and u to ordinary Python functions
f = sym.lambdify([x], f, modules="numpy")
u = sym.lambdify([x], u, modules="numpy")
resolution = 401 # no of points in plot
xcoor = linspace(Omega[0], Omega[1], resolution)
exact = f(xcoor)
approx = u(xcoor)
plot(xcoor, approx)
hold('on')
plot(xcoor, exact)
legend(['approximation', 'exact'])
savefig(filename)
All code in module approx1D.py
>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x], Omega=[1, 2])
>>> comparison_plot(f, u, Omega=[1, 2])

>>> from approx1D import *
>>> x = sym.Symbol('x')
>>> f = 10*(x-1)**2-1
>>> u, c = least_squares(f=f, psi=[1, x, x**2], Omega=[1, 2])
>>> print u
10*x**2 - 20*x + 9
>>> print sym.expand(f)
10*x**2 - 20*x + 9
least_squares is \( c_i=0 \) for \( i>2 \)
If \( f\in V \), least squares and projection/Galerkin give \( u=f \).
If \( f\in V \), \( f=\sum_{j\in\If}d_j\baspsi_j \), for some \( \sequencei{d} \). Then
$$
\begin{equation*}
b_i = (f,\baspsi_i) = \sum_{j\in\If}d_j(\baspsi_j, \baspsi_i)
= \sum_{j\in\If} d_jA_{i,j}
\end{equation*}
$$
The linear system \( \sum_j A_{i,j}c_j = b_i \), \( i\in\If \), is then
$$
\begin{equation*}
\sum_{j\in\If}c_jA_{i,j} = \sum_{j\in\If}d_jA_{i,j},\quad i\in\If
\end{equation*}
$$
which implies that \( c_i=d_i \) for \( i\in\If \) and \( u \) is identical to \( f \).
The previous computations were symbolic. What if we solve the linear system numerically with standard arrays?
That is, \( f \) is parabola, but we approximate with
$$ u(x) = c_0 + c_1x + c_2x^2 + c_3x^3 +\cdots + c_Nx^N $$
We expect \( c_2=c_3=\cdots=c_N=0 \) since \( f\in V \) implies \( u=f \).
Will we get this result with finite precision computer arithmetic?
| exact | sympy | numpy32 | numpy64 |
|---|---|---|---|
| 9 | 9.62 | 5.57 | 8.98 |
| -20 | -23.39 | -7.65 | -19.93 |
| 10 | 17.74 | -4.50 | 9.96 |
| 0 | -9.19 | 4.13 | -0.26 |
| 0 | 5.25 | 2.99 | 0.72 |
| 0 | 0.18 | -1.21 | -0.93 |
| 0 | -2.48 | -0.41 | 0.73 |
| 0 | 1.81 | -0.013 | -0.36 |
| 0 | -0.66 | 0.08 | 0.11 |
| 0 | 0.12 | 0.04 | -0.02 |
| 0 | -0.001 | -0.02 | 0.002 |
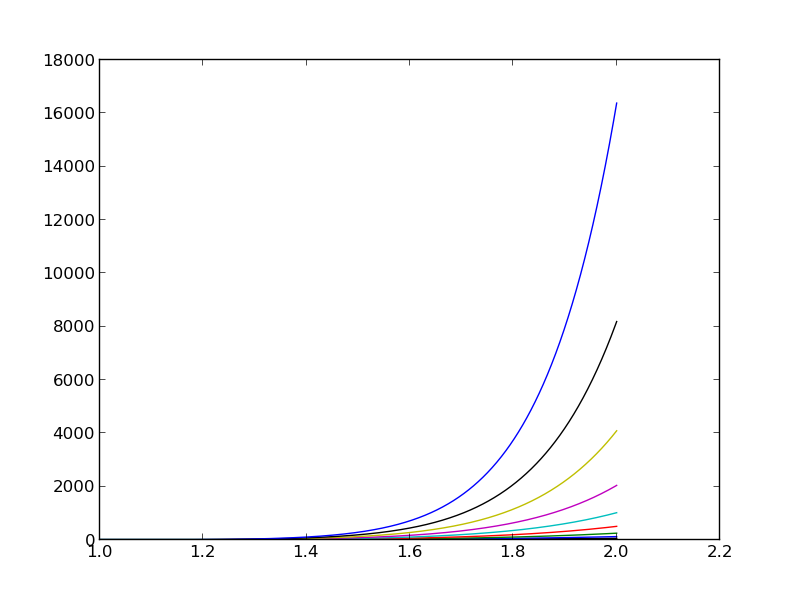
matrix and lu_solve from sympy.mpmath.fpnumpy matrix with 4-byte floatsnumpy matrix with 8-byte floatsSource or problem: the \( x^i \) functions become almost linearly dependent as \( i \) grows:
Let's approximate \( f \) by a typical Fourier series expansion
$$ u(x) = \sum_i a_i\sin i\pi x = \sum_{j=0}^Nc_j\sin((j+1)\pi x) $$
which means that
$$
\begin{equation*}
V = \hbox{span}\,\{ \sin \pi x, \sin 2\pi x,\ldots,\sin (N+1)\pi x\}
\end{equation*}
$$
Computations using the least_squares function:
N = 3
from sympy import sin, pi
psi = [sin(pi*(i+1)*x) for i in range(N+1)]
f = 10*(x-1)**2 - 1
Omega = [0, 1]
u, c = least_squares(f, psi, Omega)
comparison_plot(f, u, Omega)
Left: \( N=3 \), right: \( N=11 \):
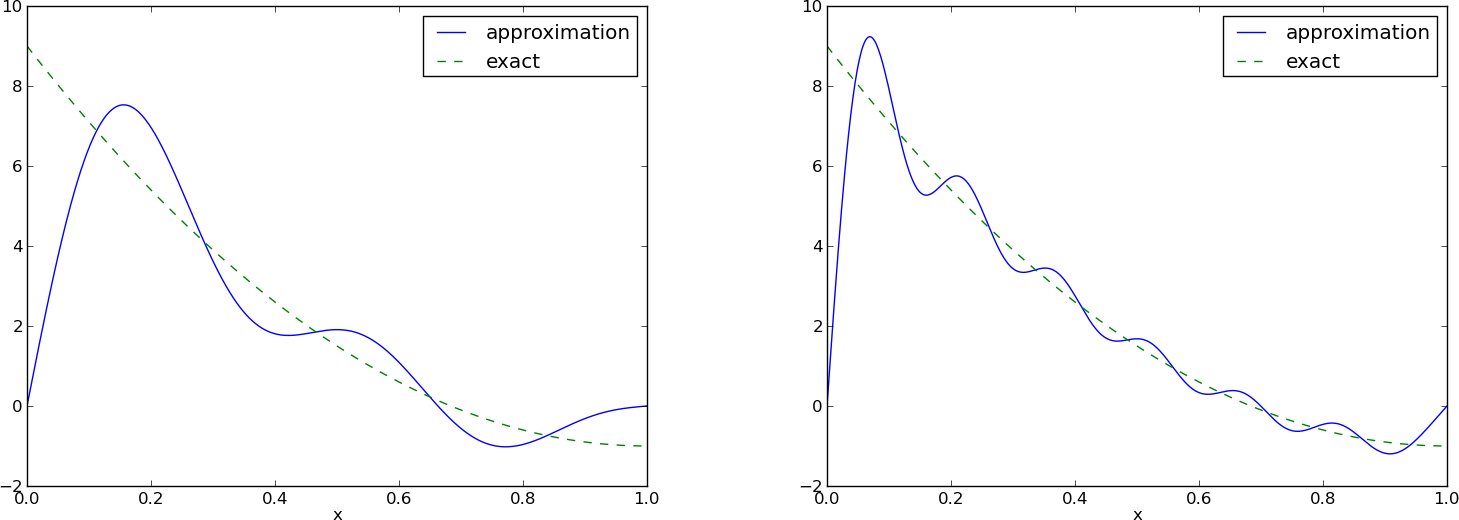
All \( \baspsi_i(0)=0 \) and hence \( u(0)=0 \neq f(0)=9 \). Similar problem at \( x=1 \). The boundary values of \( u \) are always wrong!
$$ u(x) = {\color{red}f(0)(1-x) + xf(1)} + \sum_{j\in\If} c_j\baspsi_j(x) $$
The extra terms ensure \( u(0)=f(0) \) and \( u(1)=f(1) \) and
is a strikingly good help to get a good
approximation!
\( N=3 \) vs \( N=11 \):
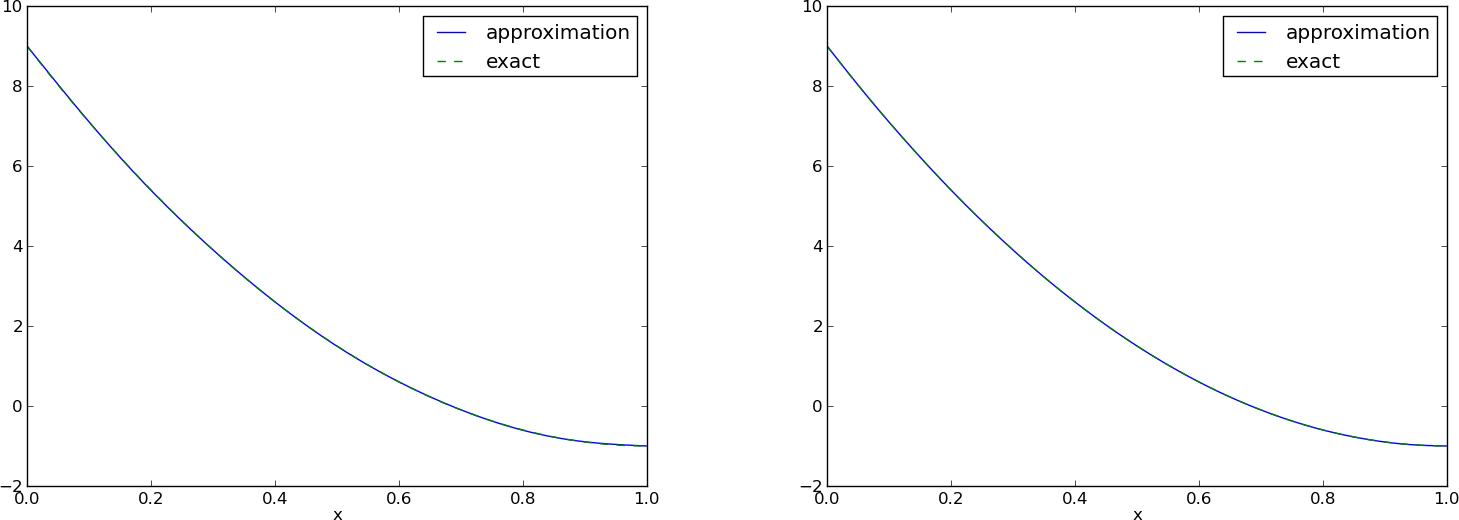
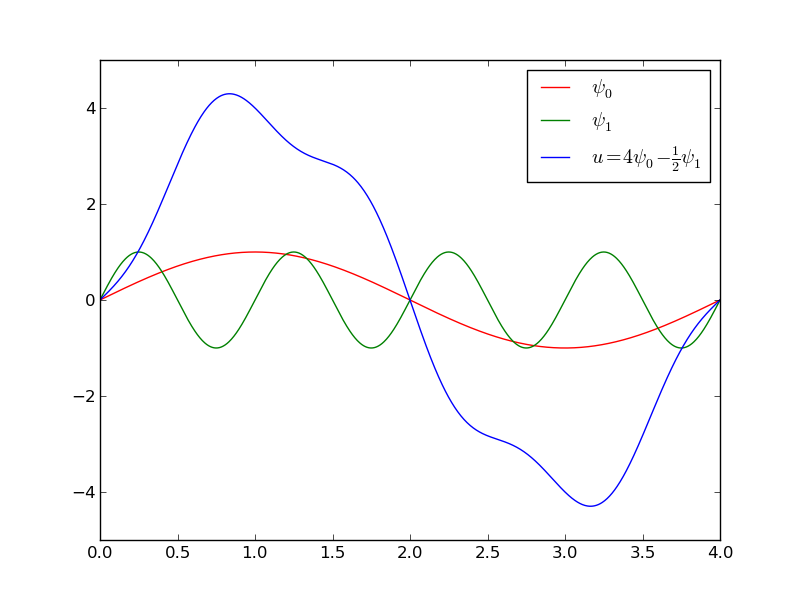
This choice of sine functions as basis functions is popular because
In general, for an orthogonal basis, \( A_{i,j} \) is diagonal and we can easily solve for \( c_i \):
$$
c_i = \frac{b_i}{A_{i,i}} = \frac{(f,\baspsi_i)}{(\baspsi_i,\baspsi_i)}
$$
def least_squares_orth(f, psi, Omega):
N = len(psi) - 1
A = [0]*(N+1)
b = [0]*(N+1)
x = sym.Symbol('x')
for i in range(N+1):
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
b[i] = sym.integrate(psi[i]*f, (x, Omega[0], Omega[1]))
c = [b[i]/A[i] for i in range(len(b))]
u = 0
for i in range(len(psi)):
u += c[i]*psi[i]
return u, c
Extensions:
symbolic argument).sym.Integral is returned from sym.integrate).
def least_squares_orth(f, psi, Omega, symbolic=True):
...
for i in range(N+1):
# Diagonal matrix term
A[i] = sym.integrate(psi[i]**2, (x, Omega[0], Omega[1]))
# Right-hand side term
integrand = psi[i]*f
if symbolic:
I = sym.integrate(integrand, (x, Omega[0], Omega[1]))
if not symbolic or isinstance(I, sym.Integral):
print 'numerical integration of', integrand
integrand = sym.lambdify([x], integrand)
I = sym.mpmath.quad(integrand, [Omega[0], Omega[1]])
b[i] = I
...
Assumption above: \( \int_\Omega\basphi_i^2dx \) works symbolically (but there is no guarantee!)
Here is another idea for approximating \( f(x) \) by \( u(x)=\sum_jc_j\baspsi_j \):
$$ u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i})
\quad i\in\If,N
$$
This is a linear system with no need for integration:
$$
\begin{align}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If
\tag{7}\\
A_{i,j} &= \baspsi_j(\xno{i})
\tag{8}\\
b_i &= f(\xno{i})
\tag{9}
\end{align}
$$
No symmetric matrix: \( \baspsi_j(\xno{i})\neq \baspsi_i(\xno{j}) \) in general
points holds the interpolation/collocation points
def interpolation(f, psi, points):
N = len(psi) - 1
A = sym.zeros((N+1, N+1))
b = sym.zeros((N+1, 1))
x = sym.Symbol('x')
# Turn psi and f into Python functions
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
A[i,j] = psi[j](points[i])
b[i,0] = f(points[i])
c = A.LUsolve(b)
u = 0
for i in range(len(psi)):
u += c[i,0]*psi[i](x)
return u
\( (4/3,5/3) \) vs \( (1,2) \):
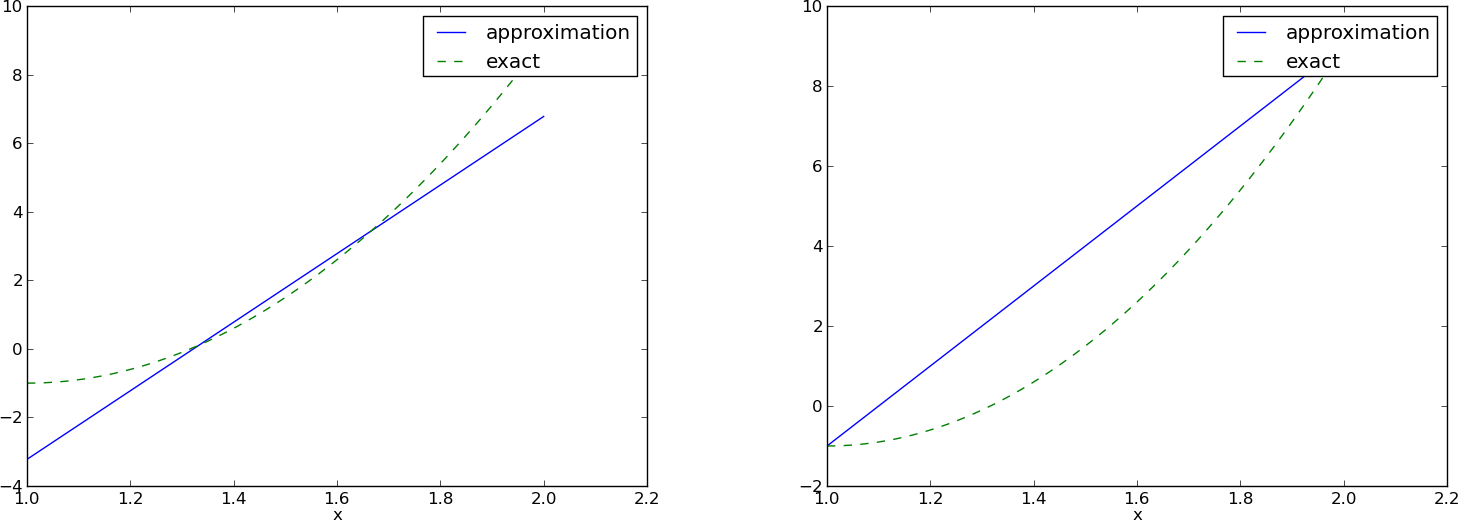
Overdetermined linear system:
$$
u(\xno{i}) = \sum_{j\in\If} c_j \baspsi_j(\xno{i}) = f(\xno{i}),
\quad i=0,1,\ldots,m
$$
$$ \sum_{j\in\If} A_{i,j}c_j = b_i,\quad i=0,1,\ldots,m $$
$$ A_{i,j} = \baspsi_j(\xno{i}),\quad
b_i = f(\xno{i})$$
$$
\begin{align*}
B_{i,j} &= \sum_k A^T_{i,k}A_{k,j} = \sum_k A_{k,i}A_{k,j}
=\sum_{k=0}^m\baspsi_i(\xno{k})\baspsi_j(\xno{k})
\\
d_i &=\sum_k A^T_{i,k}b_k = \sum_k A_{k,i}b_k =\sum_{k=0}^m
\baspsi_i(\xno{k})f(\xno{k})
\end{align*}
$$
def regression(f, psi, points):
N = len(psi) - 1
m = len(points)
# Use numpy arrays and numerical computing
B = np.zeros((N+1, N+1))
d = np.zeros(N+1)
# Wrap psi and f in Python functions rather than expressions
# so that we can evaluate psi at points[i]
x = sym.Symbol('x')
psi_sym = psi # save symbolic expression
psi = [sym.lambdify([x], psi[i]) for i in range(N+1)]
f = sym.lambdify([x], f)
for i in range(N+1):
for j in range(N+1):
B[i,j] = 0
for k in range(m+1):
B[i,j] += psi[i](points[k])*psi[j](points[k])
d[i] = 0
for k in range(m+1):
d[i] += psi[i](points[k])*f(points[k])
c = np.linalg.solve(B, d)
u = sum(c[i]*psi_sym[i] for i in range(N+1))
return u, c
import sympy as sym
x = sym.Symbol('x')
f = 10*(x-1)**2 - 1
psi = [1, x]
Omega = [1, 2]
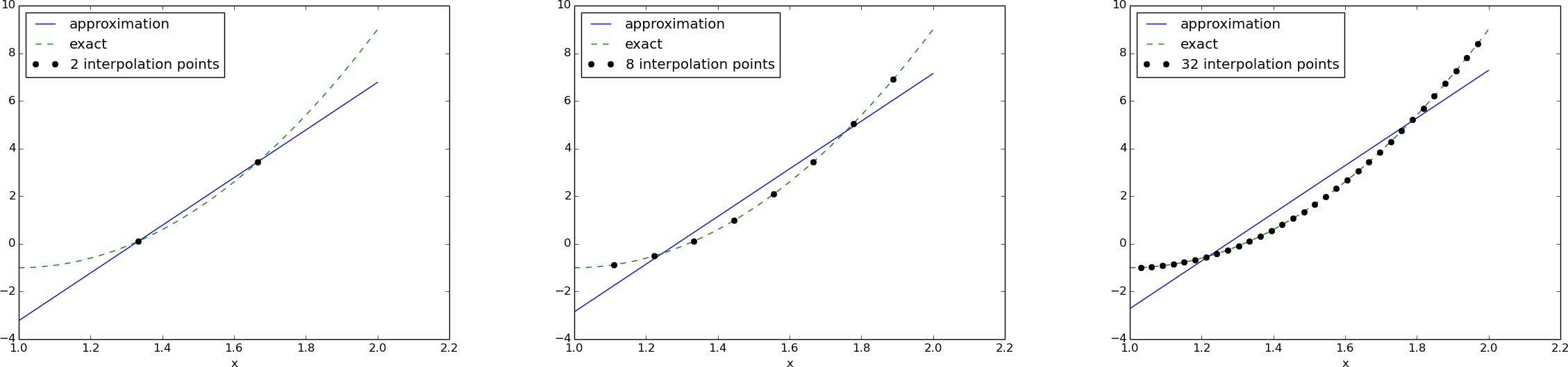
m_values = [2-1, 8-1, 64-1]
# Create m+3 points and use the inner m+1 points
for m in m_values:
points = np.linspace(Omega[0], Omega[1], m+3)[1:-1]
u, c = regression(f, psi, points)
comparison_plot(f, u, Omega, points=points,
points_legend='%d interpolation points' % (m+1))
$$
\begin{align*}
u(x) &= 10x - 13.2,\quad 2\hbox{ points}\\
u(x) &= 10x - 12.7,\quad 8\hbox{ points}\\
u(x) &= 10x - 12.7,\quad 64\hbox{ points}
\end{align*}
$$

Motivation:
The Lagrange interpolating polynomials \( \baspsi_j \) have the property that
$$ \baspsi_i(\xno{j}) =\delta_{ij},\quad \delta_{ij} =
\left\lbrace\begin{array}{ll}
1, & i=j\\
0, & i\neq j
\end{array}\right.
$$
Hence, \( c_i = f(x_i) \) and
$$
u(x) = \sum_{j\in\If} f(\xno{i})\baspsi_i(x)
$$
$$
\baspsi_i(x) =
\prod_{j=0,j\neq i}^N
\frac{x-\xno{j}}{\xno{i}-\xno{j}}
= \frac{x-x_0}{\xno{i}-x_0}\cdots\frac{x-\xno{i-1}}{\xno{i}-\xno{i-1}}\frac{x-\xno{i+1}}{\xno{i}-\xno{i+1}}
\cdots\frac{x-x_N}{\xno{i}-x_N}
$$
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
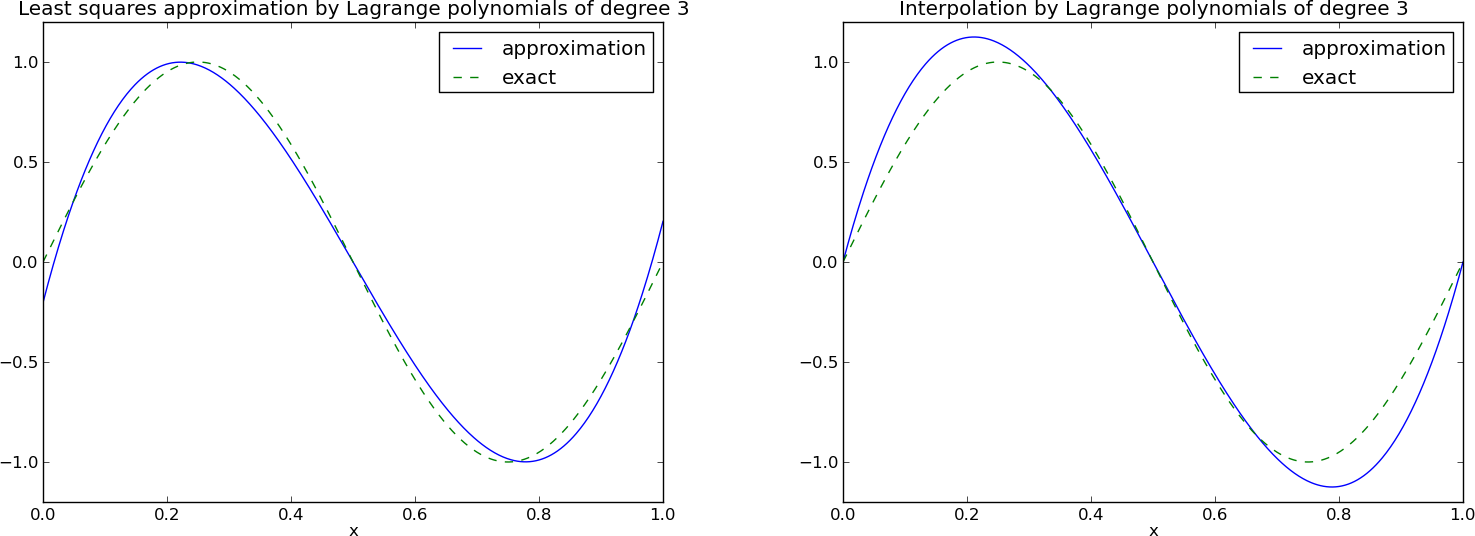
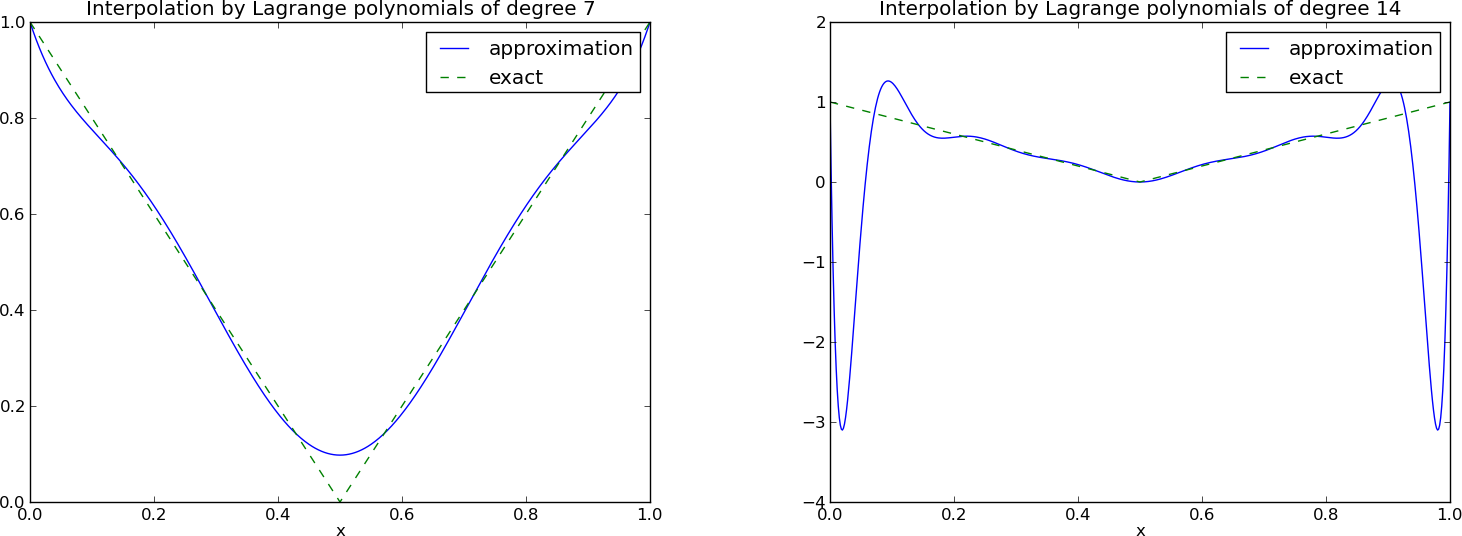
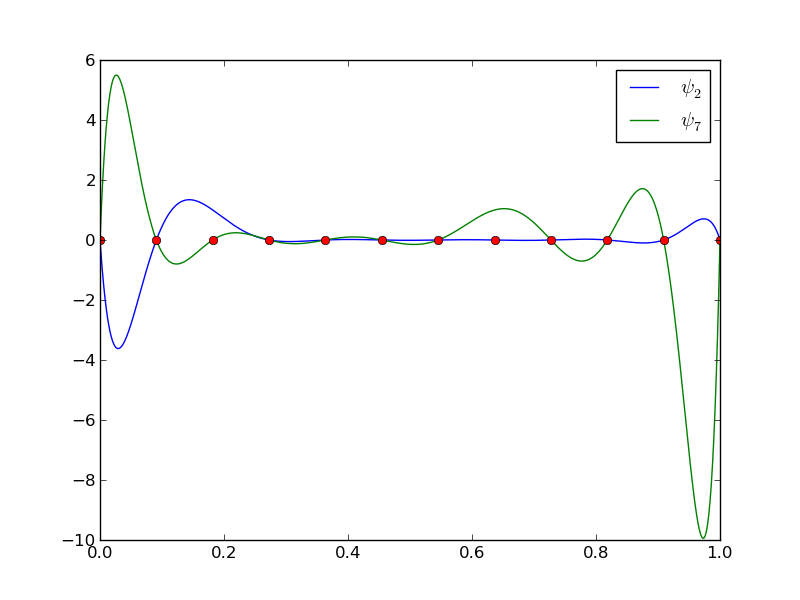
12 points, degree 11, plot of two of the Lagrange polynomials - note that they are zero at all points except one.
Problem: strong oscillations near the boundaries for larger \( N \) values.
The oscillations can be reduced by a more clever choice of interpolation points, called the Chebyshev nodes:
$$
\xno{i} = \half (a+b) + \half(b-a)\cos\left( \frac{2i+1}{2(N+1)}\pi\right),\quad i=0\ldots,N
$$
on an interval \( [a,b] \).
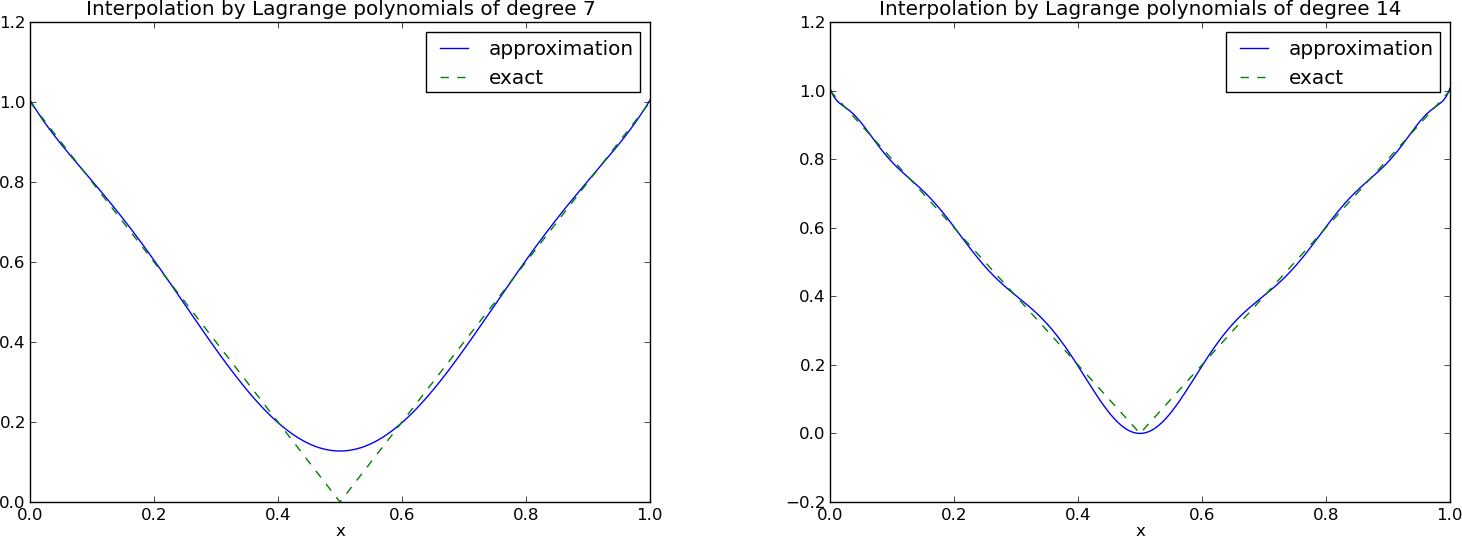
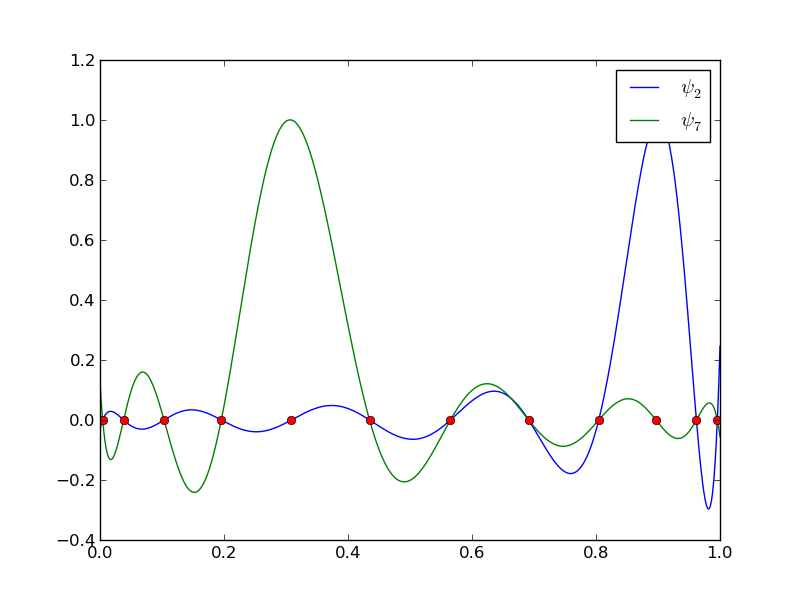
12 points, degree 11, plot of two of the Lagrange polynomials - note that they are zero at all points except one.
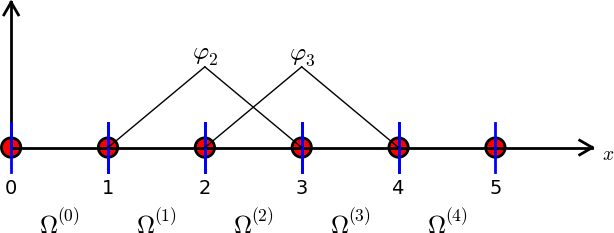

Split \( \Omega \) into \( N_e \) non-overlapping subdomains called elements:
$$
\Omega = \Omega^{(0)}\cup \cdots \cup \Omega^{(N_e)}
$$
On each element, introduce \( N_n \) points called nodes: \( \xno{0},\ldots,\xno{N_n-1} \)
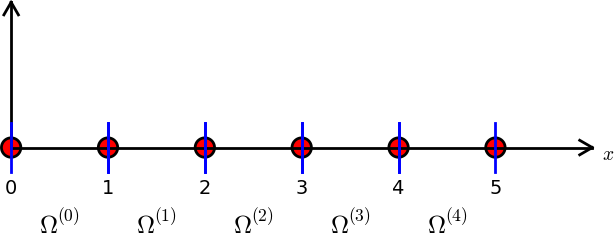
Data structure: nodes holds coordinates or nodes, elements holds the
node numbers in each element
nodes = [0, 1.2, 2.4, 3.6, 4.8, 5]
elements = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5]]

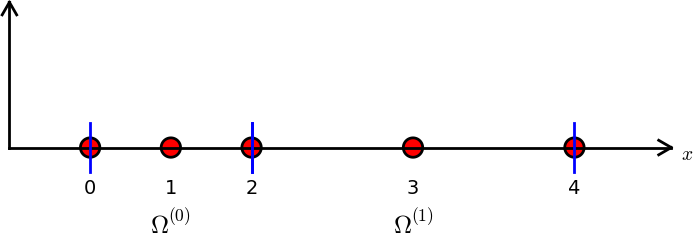
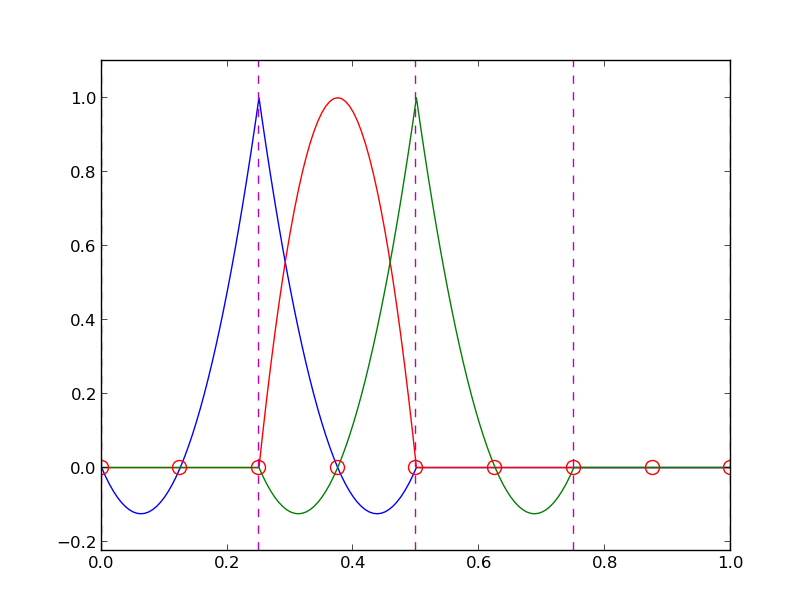
nodes = [0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1.0]
elements = [[0, 1, 2], [2, 3, 4], [4, 5, 6], [6, 7, 8]]
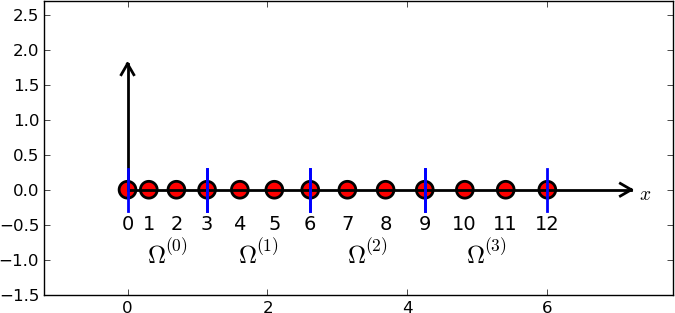
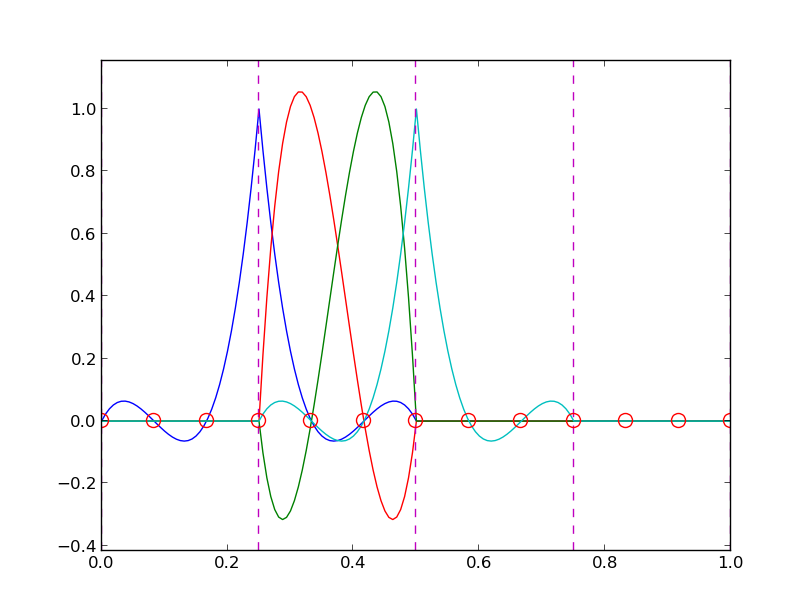
d = 3 # d+1 nodes per element
num_elements = 4
num_nodes = num_elements*d + 1
nodes = [i*0.5 for i in range(num_nodes)]
elements = [[i*d+j for j in range(d+1)] for i in range(num_elements)]
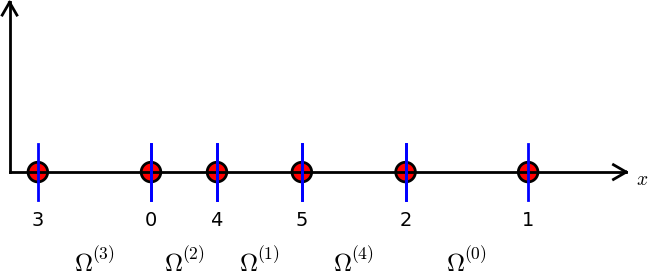
nodes = [1.5, 5.5, 4.2, 0.3, 2.2, 3.1]
elements = [[2, 1], [4, 5], [0, 4], [3, 0], [5, 2]]
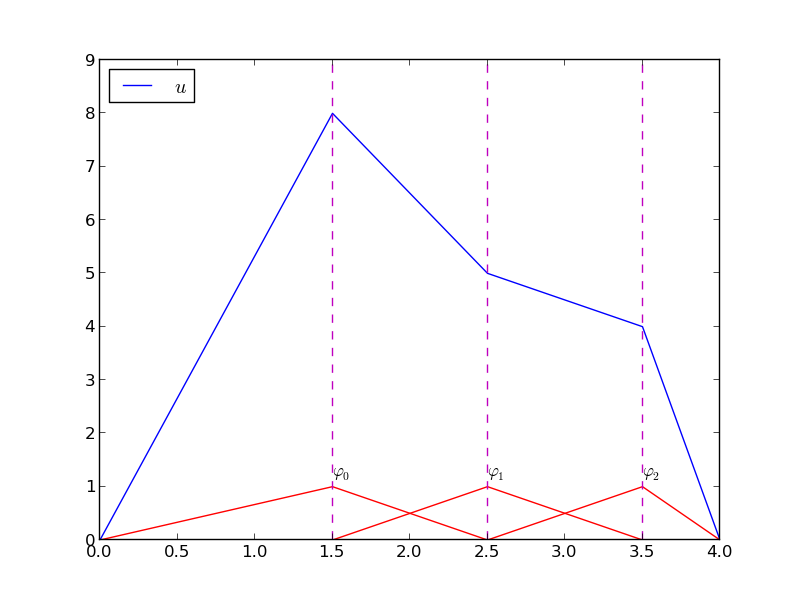
Important property: \( c_i \) is the value of \( u \) at node \( i \), \( \xno{i} \):
$$
u(\xno{i}) = \sum_{j\in\If} c_j\basphi_j(\xno{i}) =
c_i\basphi_i(\xno{i}) = c_i
$$
because \( \basphi_j(\xno{i}) =0 \) if \( i\neq j \) and \( \basphi_i(\xno{i}) =1 \)
Since \( A_{i,j}=\int\basphi_i\basphi_j\dx \), most of the elements in the coefficient matrix will be zero
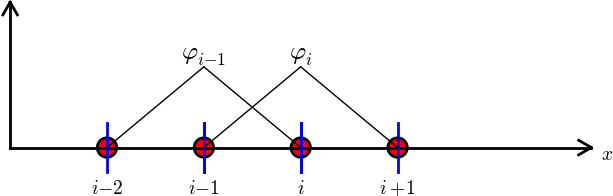

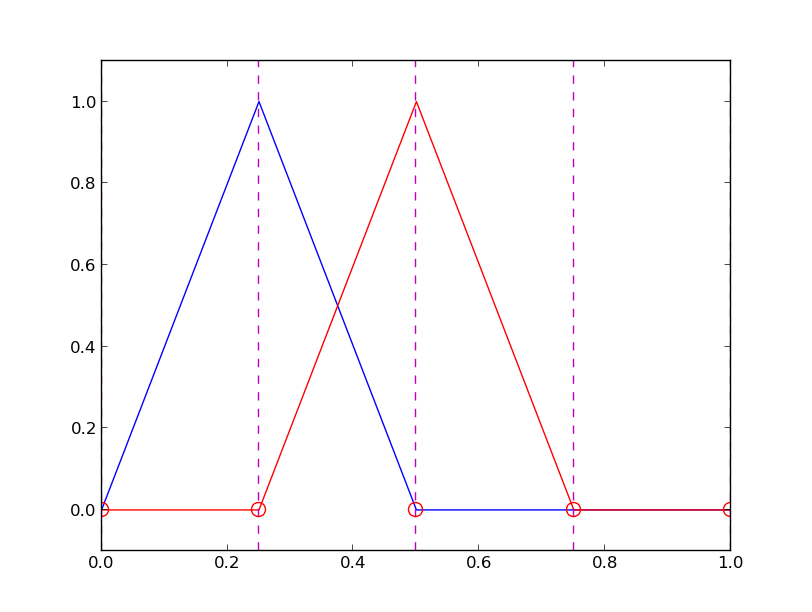
$$
\basphi_i(x) = \left\lbrace\begin{array}{ll}
0, & x < \xno{i-1}\\
(x - \xno{i-1})/h
& \xno{i-1} \leq x < \xno{i}\\
1 -
(x - x_{i})/h,
& \xno{i} \leq x < \xno{i+1}\\
0, & x\geq \xno{i+1}
\end{array}
\right.
$$



\( A_{2,3}=\int_\Omega\basphi_2\basphi_3 dx \): \( \basphi_2\basphi_3\neq 0 \) only over element 2. There,
$$ \basphi_3(x) = (x-x_2)/h,\quad \basphi_2(x) = 1- (x-x_2)/h$$
$$
A_{2,3} = \int_\Omega \basphi_2\basphi_{3}\dx =
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right) \frac{x - x_{2}}{h}
\dx = \frac{h}{6}
$$

$$ A_{2,2} =
\int_{\xno{1}}^{\xno{2}}
\left(\frac{x - \xno{1}}{h}\right)^2\dx +
\int_{\xno{2}}^{\xno{3}}
\left(1 - \frac{x - \xno{2}}{h}\right)^2\dx
= \frac{2h}{3}
$$

$$ A_{i,i-1} = \int_\Omega \basphi_i\basphi_{i-1}\dx = \hbox{?}$$
$$
\begin{align*}
A_{i,i-1} &= \int_\Omega \basphi_i\basphi_{i-1}\dx\\
&=
\underbrace{\int_{\xno{i-2}}^{\xno{i-1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_i=0} +
\int_{\xno{i-1}}^{\xno{i}} \basphi_i\basphi_{i-1}\dx +
\underbrace{\int_{\xno{i}}^{\xno{i+1}} \basphi_i\basphi_{i-1}\dx}_{\basphi_{i-1}=0}\\
&= \int_{\xno{i-1}}^{\xno{i}}
\underbrace{\left(\frac{x - x_{i}}{h}\right)}_{\basphi_i(x)}
\underbrace{\left(1 - \frac{x - \xno{i-1}}{h}\right)}_{\basphi_{i-1}(x)} \dx =
\frac{h}{6}
\end{align*}
$$
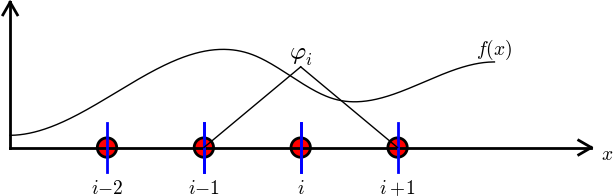
$$
b_i = \int_\Omega\basphi_i(x)f(x)\dx
= \int_{\xno{i-1}}^{\xno{i}} \frac{x - \xno{i-1}}{h} f(x)\dx
+ \int_{x_{i}}^{\xno{i+1}} \left(1 - \frac{x - x_{i}}{h}\right) f(x)
\dx
$$
Need a specific \( f(x) \) to do more...
$$
\begin{equation*}
A = \frac{h}{6}\left(\begin{array}{ccc}
2 & 1 & 0\\
1 & 4 & 1\\
0 & 1 & 2
\end{array}\right),\quad
b = \frac{h^2}{12}\left(\begin{array}{c}
2 - 3h\\
12 - 14h\\
10 -17h
\end{array}\right)
\end{equation*}
$$
$$
\begin{equation*} c_0 = \frac{h^2}{6},\quad c_1 = h - \frac{5}{6}h^2,\quad
c_2 = 2h - \frac{23}{6}h^2
\end{equation*}
$$
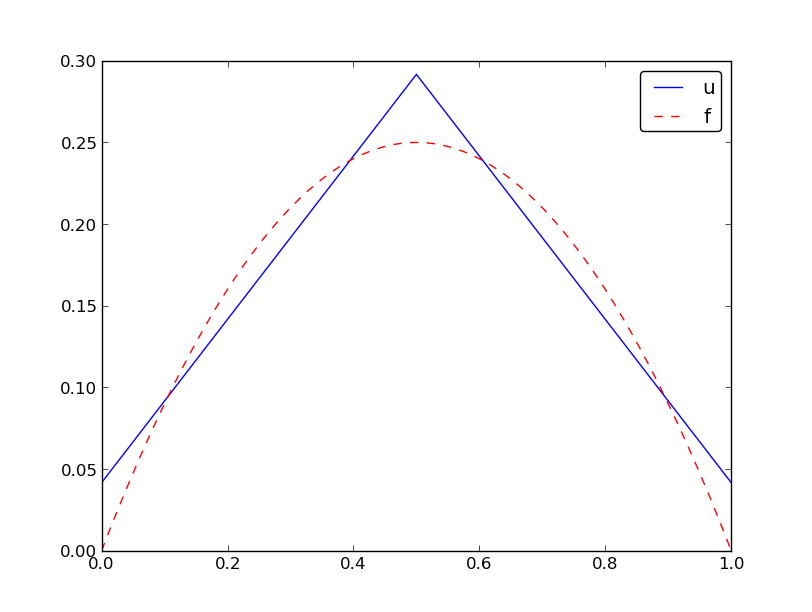
$$
\begin{equation*} u(x)=c_0\basphi_0(x) + c_1\basphi_1(x) + c_2\basphi_2(x)\end{equation*}
$$
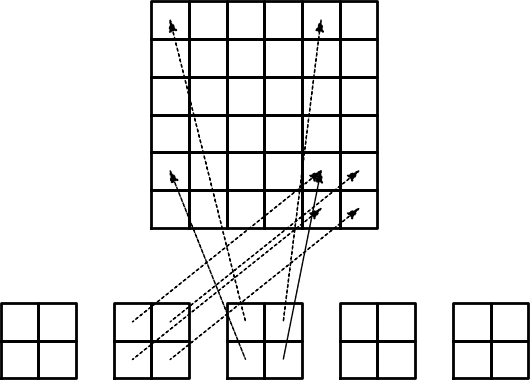
$$
A_{i,j} = \int_\Omega\basphi_i\basphi_jdx =
\sum_{e} \int_{\Omega^{(e)}} \basphi_i\basphi_jdx,\quad
A^{(e)}_{i,j}=\int_{\Omega^{(e)}} \basphi_i\basphi_jdx
$$
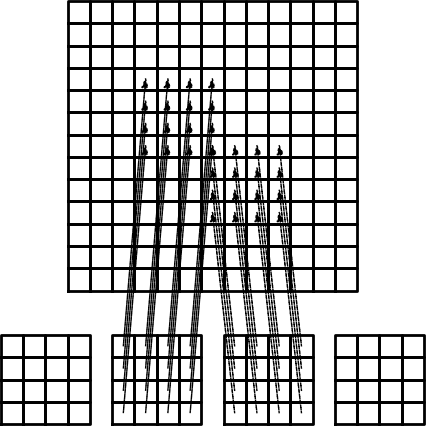
Important observations:

$$
\tilde A^{(e)} = \{ \tilde A^{(e)}_{r,s}\},\quad
\tilde A^{(e)}_{r,s} =
\int_{\Omega^{(e)}}\basphi_{q(e,r)}\basphi_{q(e,s)}dx,
\quad r,s\in\Ifd=\{0,\ldots,d\}
$$
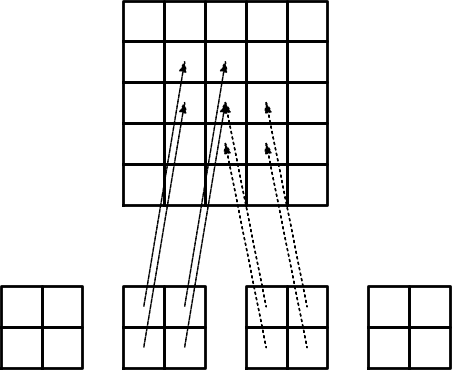
Now,
i=elements[e][r])
$$
A_{q(e,r),q(e,s)} := A_{q(e,r),q(e,s)} + \tilde A^{(e)}_{r,s},\quad
r,s\in\Ifd
$$

$$
b_i = \int_\Omega f(x)\basphi_i(x)dx =
\sum_{e} \int_{\Omega^{(e)}} f(x)\basphi_i(x)dx,\quad
b^{(e)}_{i}=\int_{\Omega^{(e)}} f(x)\basphi_i(x)dx
$$

Important observations:
Assembly:
$$
b_{q(e,r)} := b_{q(e,r)} + \tilde b^{(e)}_{r},\quad
r\in\Ifd
$$
Instead of computing
$$
\begin{equation*} \tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
= \int_{x_L}^{x_R}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
\end{equation*}
$$
we now map \( [x_L, x_R] \) to
a standardized reference element domain \( [-1,1] \) with local coordinate \( X \)
$$
x = \half (x_L + x_R) + \half (x_R - x_L)X
$$
or rewritten as
$$
x = x_m + {\half}hX, \qquad x_m=(x_L+x_R)/2,\quad h=x_R-x_L
$$
Reference element integration: just change integration variable from \( x \) to \( X \). Introduce local basis function
$$
\refphi_r(X) = \basphi_{q(e,r)}(x(X))
$$
$$
\tilde A^{(e)}_{r,s} = \int_{\Omega^{(e)}}\basphi_{q(e,r)}(x)\basphi_{q(e,s)}(x)dx
= \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\underbrace{\frac{dx}{dX}}_{\det J = h/2}dX
= \int\limits_{-1}^1 \refphi_r(X)\refphi_s(X)\det J\,dX
$$
$$
\tilde b^{(e)}_{r} = \int_{\Omega^{(e)}}f(x)\basphi_{q(e,r)}(x)dx
= \int\limits_{-1}^1 f(x(X))\refphi_r(X)\det J\,dX
$$
$$
\begin{align}
\refphi_0(X) &= \half (1 - X)
\tag{10}\\
\refphi_1(X) &= \half (1 + X)
\tag{11}
\end{align}
$$
Note: simple polynomial expressions (no need to consider piecewisely defined functions)
$$
\begin{align}
\refphi_0(X) &= \half (X-1)X
\tag{12}\\
\refphi_1(X) &= 1 - X^2
\tag{13}\\
\refphi_2(X) &= \half (X+1)X
\tag{14}
\end{align}
$$
Easy to generalize to arbitrary order!
Three alternatives:
P1 elements and \( f(x)=x(1-x) \).
$$
\begin{align}
\tilde A^{(e)}_{0,0}
&= \int_{-1}^1 \refphi_0(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1-X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X)^2 dX = \frac{h}{3}
\tag{15}\\
\tilde A^{(e)}_{1,0}
&= \int_{-1}^1 \refphi_1(X)\refphi_0(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1-X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1-X^2) dX = \frac{h}{6}
\tag{16}\\
\tilde A^{(e)}_{0,1} &= \tilde A^{(e)}_{1,0}
\tag{17}\\
\tilde A^{(e)}_{1,1}
&= \int_{-1}^1 \refphi_1(X)\refphi_1(X)\frac{h}{2} dX\nonumber\\
&=\int_{-1}^1 \half(1+X)\half(1+X) \frac{h}{2} dX =
\frac{h}{8}\int_{-1}^1 (1+X)^2 dX = \frac{h}{3}
\tag{18}
\end{align}
$$
$$
\begin{align}
\tilde b^{(e)}_{0}
&= \int_{-1}^1 f(x(X))\refphi_0(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1-X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} + \frac{1}{6} h^{2} x_{m} - \frac{1}{12} h^{2} - \half h x_{m}^{2} + \half h x_{m}
\tag{19}\\
\tilde b^{(e)}_{1}
&= \int_{-1}^1 f(x(X))\refphi_1(X)\frac{h}{2} dX\nonumber\\
&= \int_{-1}^1 (x_m + \half hX)(1-(x_m + \half hX))
\half(1+X)\frac{h}{2} dX \nonumber\\
&= - \frac{1}{24} h^{3} - \frac{1}{6} h^{2} x_{m} + \frac{1}{12} h^{2} -
\half h x_{m}^{2} + \half h x_{m}
\tag{20}
\end{align}
$$
\( x_m \): element midpoint.
>>> import sympy as sym
>>> x, x_m, h, X = sym.symbols('x x_m h X')
>>> sym.integrate(h/8*(1-X)**2, (X, -1, 1))
h/3
>>> sym.integrate(h/8*(1+X)*(1-X), (X, -1, 1))
h/6
>>> x = x_m + h/2*X
>>> b_0 = sym.integrate(h/4*x*(1-x)*(1-X), (X, -1, 1))
>>> print b_0
-h**3/24 + h**2*x_m/6 - h**2/12 - h*x_m**2/2 + h*x_m/2
Can print out in LaTeX too (convenient for copying into reports):
>>> print sym.latex(b_0, mode='plain')
- \frac{1}{24} h^{3} + \frac{1}{6} h^{2} x_{m}
- \frac{1}{12} h^{2} - \half h x_{m}^{2}
+ \half h x_{m}
Let \( \refphi_r(X) \) be a Lagrange polynomial of degree d:
import sympy as sym
import numpy as np
def phi_r(r, X, d):
if isinstance(X, sym.Symbol):
h = sym.Rational(1, d) # node spacing
nodes = [2*i*h - 1 for i in range(d+1)]
else:
# assume X is numeric: use floats for nodes
nodes = np.linspace(-1, 1, d+1)
return Lagrange_polynomial(X, r, nodes)
def Lagrange_polynomial(x, i, points):
p = 1
for k in range(len(points)):
if k != i:
p *= (x - points[k])/(points[i] - points[k])
return p
def basis(d=1):
"""Return the complete basis."""
X = sym.Symbol('X')
phi = [phi_r(r, X, d) for r in range(d+1)]
return phi
def element_matrix(phi, Omega_e, symbolic=True):
n = len(phi)
A_e = sym.zeros((n, n))
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
detJ = h/2 # dx/dX
for r in range(n):
for s in range(r, n):
A_e[r,s] = sym.integrate(phi[r]*phi[s]*detJ, (X, -1, 1))
A_e[s,r] = A_e[r,s]
return A_e
>>> from fe_approx1D import *
>>> phi = basis(d=1)
>>> phi
[1/2 - X/2, 1/2 + X/2]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=True)
[h/3, h/6]
[h/6, h/3]
>>> element_matrix(phi, Omega_e=[0.1, 0.2], symbolic=False)
[0.0333333333333333, 0.0166666666666667]
[0.0166666666666667, 0.0333333333333333]
def element_vector(f, phi, Omega_e, symbolic=True):
n = len(phi)
b_e = sym.zeros((n, 1))
# Make f a function of X
X = sym.Symbol('X')
if symbolic:
h = sym.Symbol('h')
else:
h = Omega_e[1] - Omega_e[0]
x = (Omega_e[0] + Omega_e[1])/2 + h/2*X # mapping
f = f.subs('x', x) # substitute mapping formula for x
detJ = h/2 # dx/dX
for r in range(n):
b_e[r] = sym.integrate(f*phi[r]*detJ, (X, -1, 1))
return b_e
Note f.subs('x', x): replace x by \( x(X) \) such that f contains X
sympy always succeedssympy then returns an Integral object instead of a number)
def element_vector(f, phi, Omega_e, symbolic=True):
...
I = sym.integrate(f*phi[r]*detJ, (X, -1, 1)) # try...
if isinstance(I, sym.Integral):
h = Omega_e[1] - Omega_e[0] # Ensure h is numerical
detJ = h/2
integrand = sym.lambdify([X], f*phi[r]*detJ)
I = sym.mpmath.quad(integrand, [-1, 1])
b_e[r] = I
...
def assemble(nodes, elements, phi, f, symbolic=True):
N_n, N_e = len(nodes), len(elements)
zeros = sym.zeros if symbolic else np.zeros
A = zeros((N_n, N_n))
b = zeros((N_n, 1))
for e in range(N_e):
Omega_e = [nodes[elements[e][0]], nodes[elements[e][-1]]]
A_e = element_matrix(phi, Omega_e, symbolic)
b_e = element_vector(f, phi, Omega_e, symbolic)
for r in range(len(elements[e])):
for s in range(len(elements[e])):
A[elements[e][r],elements[e][s]] += A_e[r,s]
b[elements[e][r]] += b_e[r]
return A, b
if symbolic:
c = A.LUsolve(b) # sympy arrays, symbolic Gaussian elim.
else:
c = np.linalg.solve(A, b) # numpy arrays, numerical solve
Note: the symbolic computation of A, b and A.LUsolve(b)
can be very tedious.
>>> h, x = sym.symbols('h x')
>>> nodes = [0, h, 2*h]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0]
[h/6, 2*h/3, h/6]
[ 0, h/6, h/3]
>>> b
[ h**2/6 - h**3/12]
[ h**2 - 7*h**3/6]
[5*h**2/6 - 17*h**3/12]
>>> c = A.LUsolve(b)
>>> c
[ h**2/6]
[12*(7*h**2/12 - 35*h**3/72)/(7*h)]
[ 7*(4*h**2/7 - 23*h**3/21)/(2*h)]
>>> nodes = [0, 0.5, 1]
>>> elements = [[0, 1], [1, 2]]
>>> phi = basis(d=1)
>>> x = sym.Symbol('x')
>>> f = x*(1-x)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=False)
>>> A
[ 0.166666666666667, 0.0833333333333333, 0]
[0.0833333333333333, 0.333333333333333, 0.0833333333333333]
[ 0, 0.0833333333333333, 0.166666666666667]
>>> b
[ 0.03125]
[0.104166666666667]
[ 0.03125]
>>> c = A.LUsolve(b)
>>> c
[0.0416666666666666]
[ 0.291666666666667]
[0.0416666666666666]
>>> d=1; N_e=8; Omega=[0,1] # 8 linear elements on [0,1]
>>> phi = basis(d)
>>> f = x*(1-x)
>>> nodes, elements = mesh_symbolic(N_e, d, Omega)
>>> A, b = assemble(nodes, elements, phi, f, symbolic=True)
>>> A
[h/3, h/6, 0, 0, 0, 0, 0, 0, 0]
[h/6, 2*h/3, h/6, 0, 0, 0, 0, 0, 0]
[ 0, h/6, 2*h/3, h/6, 0, 0, 0, 0, 0]
[ 0, 0, h/6, 2*h/3, h/6, 0, 0, 0, 0]
[ 0, 0, 0, h/6, 2*h/3, h/6, 0, 0, 0]
[ 0, 0, 0, 0, h/6, 2*h/3, h/6, 0, 0]
[ 0, 0, 0, 0, 0, h/6, 2*h/3, h/6, 0]
[ 0, 0, 0, 0, 0, 0, h/6, 2*h/3, h/6]
[ 0, 0, 0, 0, 0, 0, 0, h/6, h/3]
Note: do this by hand to understand what is going on!
$$
A = \frac{h}{6}
\left(
\begin{array}{cccccccccc}
2 & 1 & 0
&\cdots & \cdots & \cdots & \cdots & \cdots & 0 \\
1 & 4 & 1 & \ddots & & & & & \vdots \\
0 & 1 & 4 & 1 &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & 1 & 4 & 1 & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & 1 & 4 & 1 \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & 1 & 2
\end{array}
\right)
$$
$$
A = \frac{h}{30}
\left(
\begin{array}{ccccccccc}
4 & 2 & - 1 & 0
& 0 & 0 & 0 & 0 & 0\\
2 & 16 & 2
& 0 & 0 & 0 & 0 & 0 & 0\\- 1 & 2 &
8 & 2 & - 1 & 0 & 0 & 0 & 0\\
0 & 0 & 2 & 16 & 2 & 0 & 0 & 0 & 0\\
0 & 0 & - 1 & 2 & 8 & 2 & - 1 & 0 & 0\\
0 & 0 & 0 & 0 & 2 & 16 & 2 & 0 & 0\\
0 & 0 & 0 & 0 & - 1 & 2 & 8 & 2 & - 1
\\0 & 0 & 0 & 0 & 0 & 0 &
2 & 16 & 2\\0 & 0 & 0 & 0 & 0
& 0 & - 1 & 2 & 4
\end{array}
\right)
$$
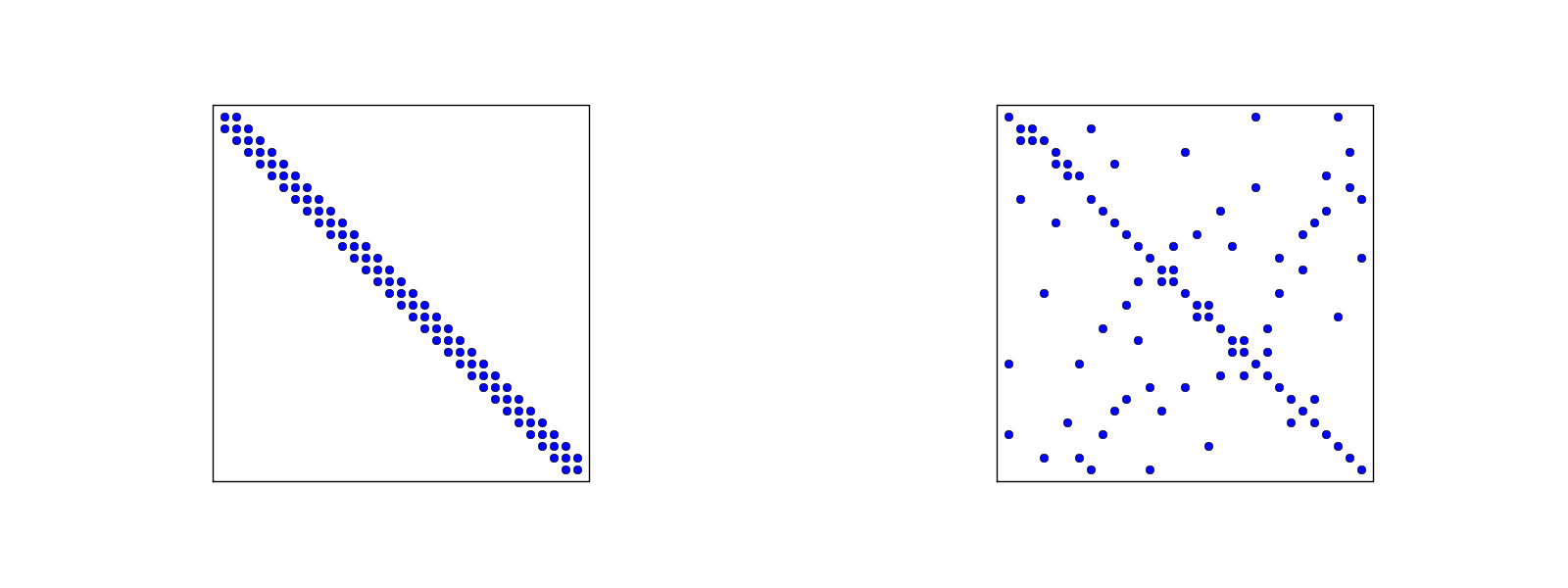
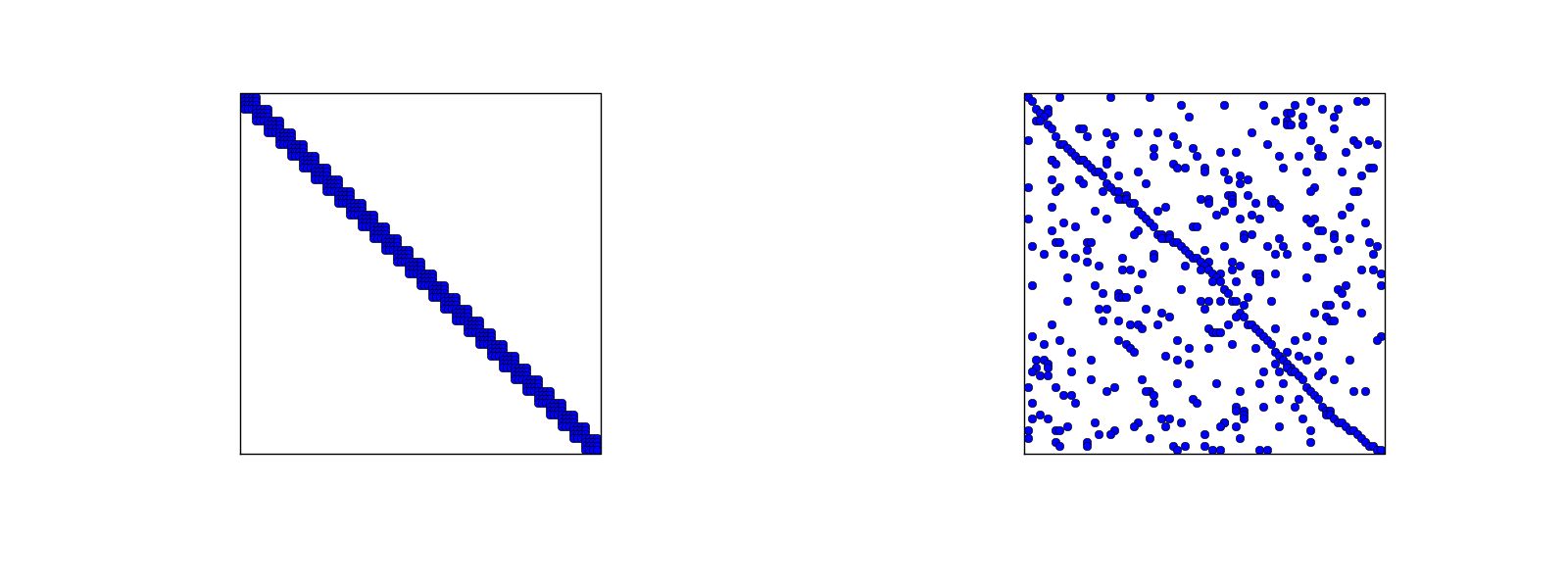
The minimum storage requirements for the coefficient matrix \( A_{i,j} \):
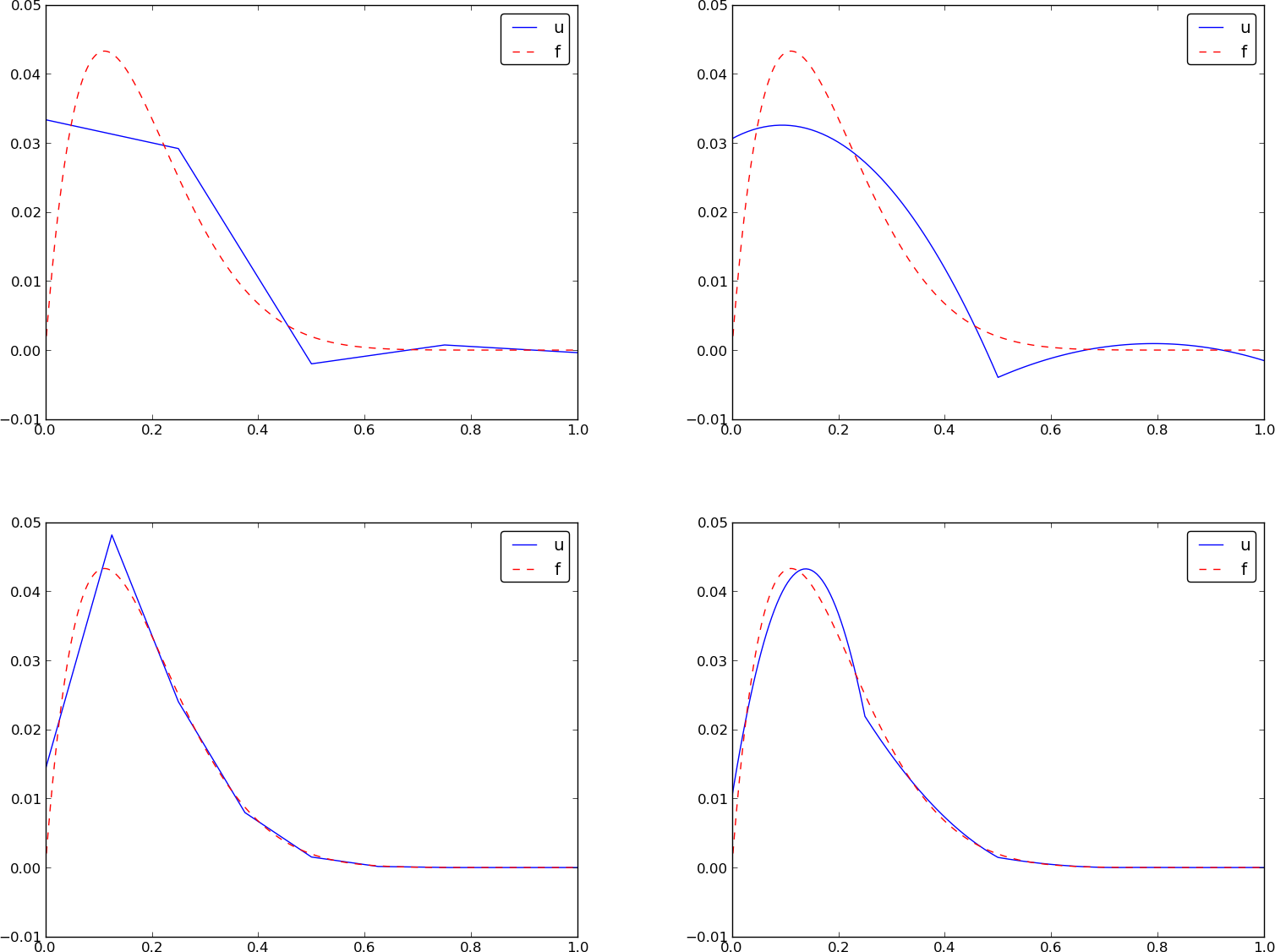
scipy.sparse packageCompute a mesh with \( N_e \) elements, basis functions of degree \( d \), and approximate a given symbolic expression \( f(x) \) by a finite element expansion \( u(x) = \sum_jc_j\basphi_j(x) \):
import sympy as sym
from fe_approx1D import approximate
x = sym.Symbol('x')
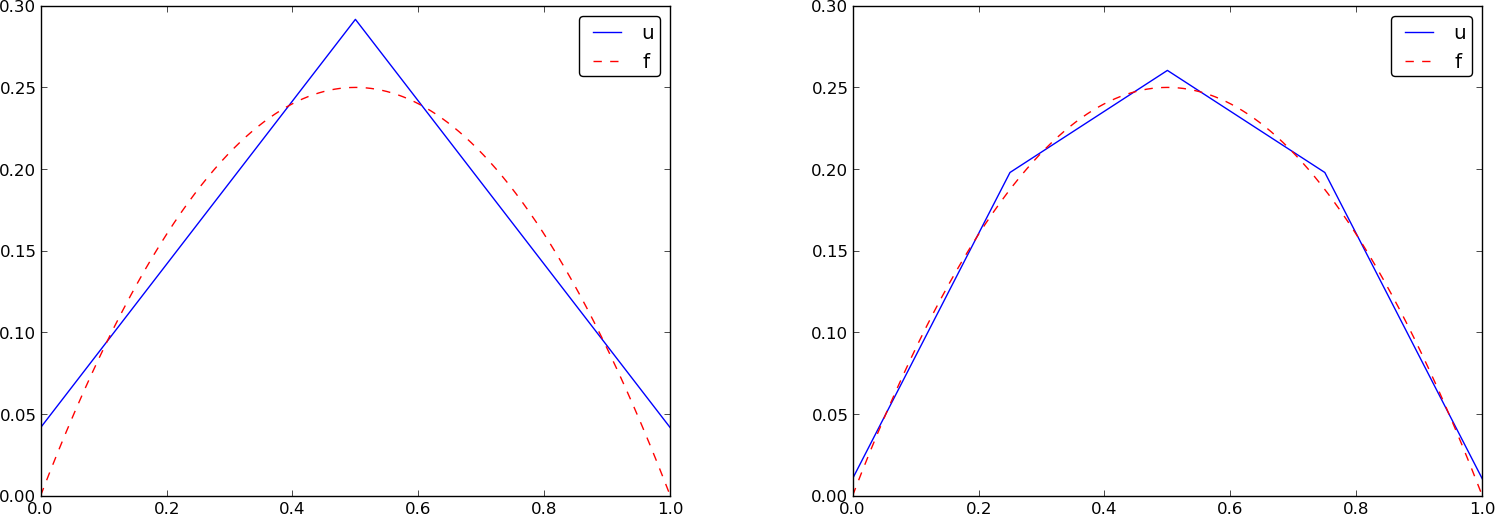
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=4)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=2)
approximate(f=x*(1-x)**8, symbolic=False, d=1, N_e=8)
approximate(f=x*(1-x)**8, symbolic=False, d=2, N_e=4)
Let \( \{\xno{i}\}_{i\in\If} \) be the nodes in the mesh. Collocation/interpolation means
$$
u(\xno{i})=f(\xno{i}),\quad i\in\If,
$$
which translates to
$$ \sum_{j\in\If} c_j \basphi_j(\xno{i}) = f(\xno{i}),$$
but \( \basphi_j(\xno{i})=0 \) if \( i\neq j \) so the sum collapses to one
term \( c_i\basphi_i(\xno{i}) = c_i \), and we have the result
$$
c_i = f(\xno{i})
$$
Same result as the standard finite difference approach, but finite elements define \( u \) also between the \( \xno{i} \) points
The P1 finite element machinery results in a linear system where equation no \( i \) is
$$
\frac{h}{6}(u_{i-1} + 4u_i + u_{i+1}) = (f,\basphi_i)
$$
Note:
Rewrite the left-hand side of finite element equation no \( i \):
$$
h(u_i + \frac{1}{6}(u_{i-1} - 2u_i + u_{i+1})) = [h(u + \frac{h^2}{6}D_x D_x u)]_i
$$
This is the standard finite difference approximation of
$$ h(u + \frac{h^2}{6}u'')$$
$$ (f,\basphi_i) = \int_{\xno{i-1}}^{\xno{i}} f(x)\frac{1}{h} (x - \xno{i-1}) dx
+ \int_{\xno{i}}^{\xno{i+1}} f(x)\frac{1}{h}(1 - (x - x_{i})) dx
$$
Cannot do much unless we specialize \( f \) or use numerical integration.
Trapezoidal rule using the nodes:
$$ (f,\basphi_i) = \int_\Omega f\basphi_i dx\approx h\half(
f(\xno{0})\basphi_i(\xno{0}) + f(\xno{N})\basphi_i(\xno{N}))
+ h\sum_{j=1}^{N-1} f(\xno{j})\basphi_i(\xno{j})
$$
\( \basphi_i(\xno{j})=\delta_{ij} \), so this formula collapses to one term:
$$
(f,\basphi_i) \approx hf(\xno{i}),\quad i=1,\ldots,N-1\thinspace.
$$
Same result as in collocation (interpolation) and the finite difference method!
$$ \int_\Omega g(x)dx \approx \frac{h}{6}\left( g(\xno{0}) +
2\sum_{j=1}^{N-1} g(\xno{j})
+ 4\sum_{j=0}^{N-1} g(\xno{j+\half}) + f(\xno{2N})\right),
$$
Our case: \( g=f\basphi_i \). The sums collapse because \( \basphi_i=0 \) at most of
the points.
$$
(f,\basphi_i) \approx \frac{h}{3}(f_{i-\half} + f_i + f_{i+\half})
$$
Conclusions:
With Trapezoidal integration of \( (f,\basphi_i) \), the finite element method essentially solve
$$
u + \frac{h^2}{6} u'' = f,\quad u'(0)=u'(L)=0,
$$
by the finite difference method
$$
[u + \frac{h^2}{6} D_x D_x u = f]_i
$$
With Simpson integration of \( (f,\basphi_i) \) we essentially solve
$$
[u + \frac{h^2}{6} D_x D_x u = \bar f]_i,
$$
where
$$ \bar f_i = \frac{1}{3}(f_{i-1/2} + f_i + f_{i+1/2}) $$
Note: as \( h\rightarrow 0 \), \( hu''\rightarrow 0 \) and \( \bar f_i\rightarrow f_i \).
Result:
So far,
One problem:
nodes and
elements arrays away and find a more generalized element conceptvertices, cells, dof_mapvertices (equals nodes for P1 elements)cells[e][r] holds global vertex number of
local vertex no r in element e (same as elements for P1 elements)dof_map[e,r] maps local dof r in element e to global dof
number (same as elements for Pd elements)
The assembly process now applies dof_map:
A[dof_map[e][r], dof_map[e][s]] += A_e[r,s]
b[dof_map[e][r]] += b_e[r]

vertices = [0, 0.4, 1]
cells = [[0, 1], [1, 2]]
dof_map = [[0, 1, 2], [2, 3, 4]]
Example: Same mesh, but \( u \) is piecewise constant in each cell (P0 element).
Same vertices and cells, but
dof_map = [[0], [1]]
May think of one node in the middle of each element.
We will hereafter work with cells, vertices, and dof_map.
# Use modified fe_approx1D module
from fe_approx1D_numint import *
x = sym.Symbol('x')
f = x*(1 - x)
N_e = 10
# Create mesh with P3 (cubic) elements
vertices, cells, dof_map = mesh_uniform(N_e, d=3, Omega=[0,1])
# Create basis functions on the mesh
phi = [basis(len(dof_map[e])-1) for e in range(N_e)]
# Create linear system and solve it
A, b = assemble(vertices, cells, dof_map, phi, f)
c = np.linalg.solve(A, b)
# Make very fine mesh and sample u(x) on this mesh for plotting
x_u, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=51)
plot(x_u, u)
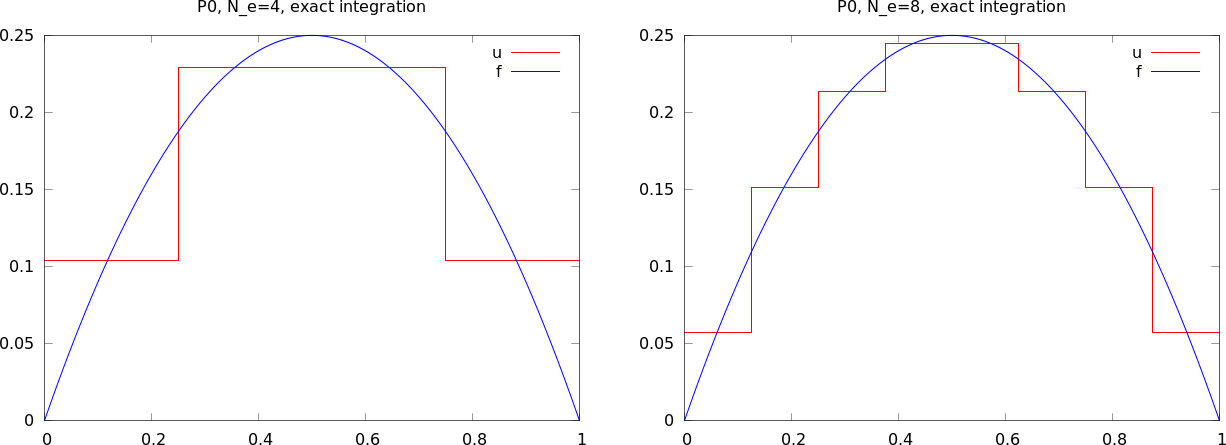
The approximate function automates the steps in the previous slide:
from fe_approx1D_numint import *
x=sym.Symbol("x")
for N_e in 4, 8:
approximate(x*(1-x), d=0, N_e=N_e, Omega=[0,1])
$$ L^2 \hbox{ error: }\quad ||e||_{L^2} =
\left(\int_{\Omega} e^2 dx\right)^{1/2}$$
Accurate approximation of the integral:
u_glob, returns x and u)
We need a version of the Trapezoidal rule valid for non-uniformly spaced points:
$$ \int_\Omega g(x) dx \approx \sum_{j=0}^{n-1} \half(g(x_j) +
g(x_{j+1}))(x_{j+1}-x_j)$$
# Given c, compute x and u values on a very fine mesh
x, u = u_glob(c, vertices, cells, dof_map,
resolution_per_element=101)
# Compute the error on the very fine mesh
e = f(x) - u
e2 = e**2
# Vectorized Trapezoidal rule
E = np.sqrt(0.5*np.sum((e2[:-1] + e2[1:])*(x[1:] - x[:-1]))
Theory and experiments show that the least squares or projection/Galerkin method in combination with Pd elements of equal length \( h \) has an error
$$
||e||_{L^2} = Ch^{d+1}
$$
where \( C \) depends on \( f \), but not on \( h \) or \( d \).
Consider a reference cell \( [-1,1] \). We introduce two nodes, \( X=-1 \) and \( X=1 \). The degrees of freedom are
Derivatives as unknowns ensure the same \( \basphi_i'(x) \) value at nodes and thereby continuous derivatives.
4 constraints on \( \refphi_r \) (1 for dof \( r \), 0 for all others):
This gives 4 linear, coupled equations for each \( \refphi_r \) to determine the 4 coefficients in the cubic polynomial
$$
\begin{align}
\refphi_0(X) &= 1 - \frac{3}{4}(X+1)^2 + \frac{1}{4}(X+1)^3
\tag{21}\\
\refphi_1(X) &= -(X+1)(1 - \half(X+1))^2
\tag{22}\\
\refphi_2(X) &= \frac{3}{4}(X+1)^2 - \half(X+1)^3
\tag{23}\\
\refphi_3(X) &= -\half(X+1)(\half(X+1)^2 - (X+1))
\tag{24}\\
\tag{25}
\end{align}
$$
$$
\int_{-1}^{1} g(X)dX \approx \sum_{j=0}^M w_jg(\bar X_j),
$$
where
Different rules correspond to different choices of points and weights
Simplest possibility: the Midpoint rule,
$$
\int_{-1}^{1} g(X)dX \approx 2g(0),\quad \bar X_0=0,\ w_0=2,
$$
Exact for linear integrands
The Trapezoidal rule:
$$
\int_{-1}^{1} g(X)dX \approx g(-1) + g(1),\quad \bar X_0=-1,\ \bar X_1=1,\ w_0=w_1=1,
$$
Simpson's rule:
$$
\int_{-1}^{1} g(X)dX \approx \frac{1}{3}\left(g(-1) + 4g(0)
+ g(1)\right),
$$
where
$$
\bar X_0=-1,\ \bar X_1=0,\ \bar X_2=1,\ w_0=w_2=\frac{1}{3},\ w_1=\frac{4}{3}
$$
$$
\begin{align}
M=1&:\quad \bar X_0=-\frac{1}{\sqrt{3}},\
\bar X_1=\frac{1}{\sqrt{3}},\ w_0=w_1=1
\tag{26}\\
M=2&:\quad \bar X_0=-\sqrt{\frac{3}{{5}}},\ \bar X_0=0,\
\bar X_2= \sqrt{\frac{3}{{5}}},\ w_0=w_2=\frac{5}{9},\ w_1=\frac{8}{9}
\tag{27}
\end{align}
$$
See numint.py for a large collection of Gauss-Legendre rules.
All the concepts and algorithms developed for approximation of 1D functions \( f(x) \) can readily be extended to 2D functions \( f(x,y) \) and 3D functions \( f(x,y,z) \). Key formulas stay the same.
Inner product in 2D:
$$
(f,g) = \int_\Omega f(x,y)g(x,y) dx dy
$$
Least squares and project/Galerkin lead to a linear system
$$
\begin{align*}
\sum_{j\in\If} A_{i,j}c_j &= b_i,\quad i\in\If\\
A_{i,j} &= (\baspsi_i,\baspsi_j)\\
b_i &= (f,\baspsi_i)
\end{align*}
$$
Challenge: How to construct 2D basis functions \( \baspsi_i(x,y) \)?
Use a 1D basis for \( x \) variation and a similar for \( y \) variation:
$$
\begin{align}
V_x &= \mbox{span}\{ \hat\baspsi_0(x),\ldots,\hat\baspsi_{N_x}(x)\}
\tag{28}\\
V_y &= \mbox{span}\{ \hat\baspsi_0(y),\ldots,\hat\baspsi_{N_y}(y)\}
\tag{29}
\end{align}
$$
The 2D vector space can be defined as a tensor product \( V = V_x\otimes V_y \) with basis functions
$$
\baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y)
\quad p\in\Ix,q\in\Iy\tp
$$
Given two vectors \( a=(a_0,\ldots,a_M) \) and \( b=(b_0,\ldots,b_N) \) their outer tensor product, also called the dyadic product, is \( p=a\otimes b \), defined through
$$ p_{i,j}=a_ib_j,\quad i=0,\ldots,M,\ j=0,\ldots,N\tp$$
Note: \( p \) has two indices (as a matrix or two-dimensional array)
Example: 2D basis as tensor product of 1D spaces,
$$ \baspsi_{p,q}(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad p\in\Ix,q\in\Iy$$
The 2D basis can employ a double index and double sum:
$$ u = \sum_{p\in\Ix}\sum_{q\in\Iy} c_{p,q}\baspsi_{p,q}(x,y)
$$
Or just a single index:
$$ u = \sum_{j\in\If} c_j\baspsi_j(x,y)$$
with an index mapping \( (p,q)\rightarrow i \):
$$
\baspsi_i(x,y) = \hat\baspsi_p(x)\hat\baspsi_q(y),
\quad i=p (N_y+1) + q\hbox{ or } i=q (N_x+1) + p
$$
In 1D we use the basis
$$ \{ 1, x \} $$
2D tensor product (all combinations):
$$ \baspsi_{0,0}=1,\quad \baspsi_{1,0}=x, \quad \baspsi_{0,1}=y,
\quad \baspsi_{1,1}=xy
$$
or with a single index:
$$ \baspsi_0=1,\quad \baspsi_1=x, \quad \baspsi_2=y,\quad\baspsi_3 =xy
$$
See notes for details of a hand-calculation.
Quadratic \( f(x,y) = (1+x^2)(1+2y^2) \) (left), bilinear \( u \) (right):
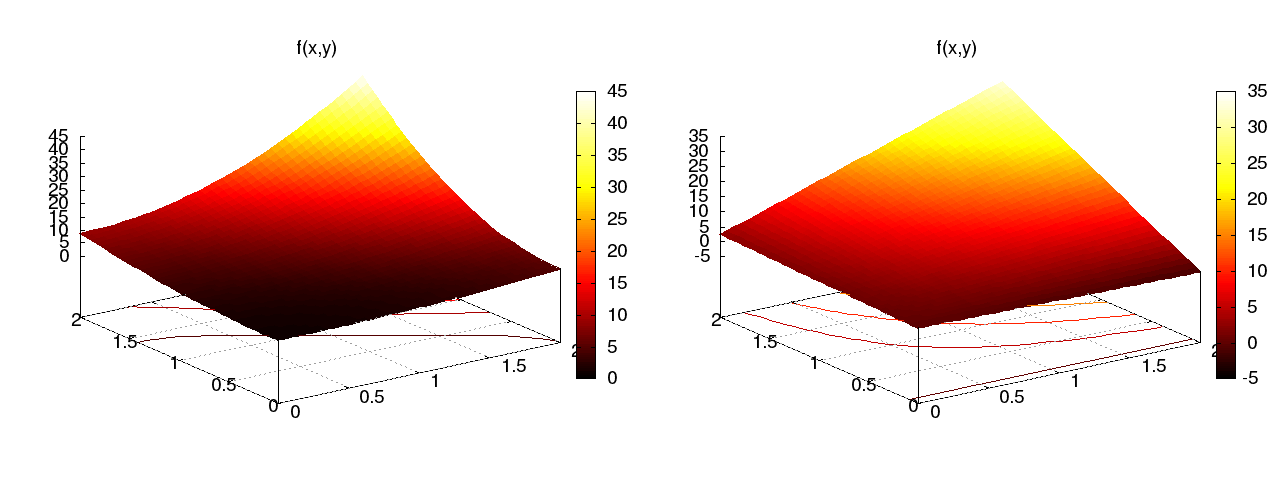
Very small modification of approx1D.py:
Omega = [[0, L_x], [0, L_y]]
import sympy as sym
integrand = psi[i]*psi[j]
I = sym.integrate(integrand,
(x, Omega[0][0], Omega[0][1]),
(y, Omega[1][0], Omega[1][1]))
# Fall back on numerical integration if symbolic integration
# was unsuccessful
if isinstance(I, sym.Integral):
integrand = sym.lambdify([x,y], integrand)
I = sym.mpmath.quad(integrand,
[Omega[0][0], Omega[0][1]],
[Omega[1][0], Omega[1][1]])
Tensor product of 1D "Taylor-style" polynomials \( x^i \):
def taylor(x, y, Nx, Ny):
return [x**i*y**j for i in range(Nx+1) for j in range(Ny+1)]
Tensor product of 1D sine functions \( \sin((i+1)\pi x) \):
def sines(x, y, Nx, Ny):
return [sym.sin(sym.pi*(i+1)*x)*sym.sin(sym.pi*(j+1)*y)
for i in range(Nx+1) for j in range(Ny+1)]
Complete code in approx2D.py
\( f(x,y) = (1+x^2)(1+2y^2) \)
>>> from approx2D import *
>>> f = (1+x**2)*(1+2*y**2)
>>> psi = taylor(x, y, 1, 1)
>>> Omega = [[0, 2], [0, 2]]
>>> u, c = least_squares(f, psi, Omega)
>>> print u
8*x*y - 2*x/3 + 4*y/3 - 1/9
>>> print sym.expand(f)
2*x**2*y**2 + x**2 + 2*y**2 + 1
Add higher powers to the basis such that \( f\in V \):
>>> psi = taylor(x, y, 2, 2)
>>> u, c = least_squares(f, psi, Omega)
>>> print u
2*x**2*y**2 + x**2 + 2*y**2 + 1
>>> print u-f
0
Expected: \( u=f \) when \( f\in V \)
Key idea:
$$ V = V_x\otimes V_y\otimes V_z$$
$$
\begin{align*}
a^{(q)} &= (a^{(q)}_0,\ldots,a^{(q)}_{N_q}),\quad q=0,\ldots,m\\
p &= a^{(0)}\otimes\cdots\otimes a^{(m)}\\
p_{i_0,i_1,\ldots,i_m} &= a^{(0)}_{i_1}a^{(1)}_{i_1}\cdots a^{(m)}_{i_m}
\end{align*}
$$
$$
\begin{align*}
\baspsi_{p,q,r}(x,y,z) &= \hat\baspsi_p(x)\hat\baspsi_q(y)\hat\baspsi_r(z)\\
u(x,y,z) &= \sum_{p\in\Ix}\sum_{q\in\Iy}\sum_{r\in\Iz} c_{p,q,r}
\baspsi_{p,q,r}(x,y,z)
\end{align*}
$$
The two great advantages of the finite element method:
Finite elements in 1D: mostly for learning, insight, debugging
2D:
3D:
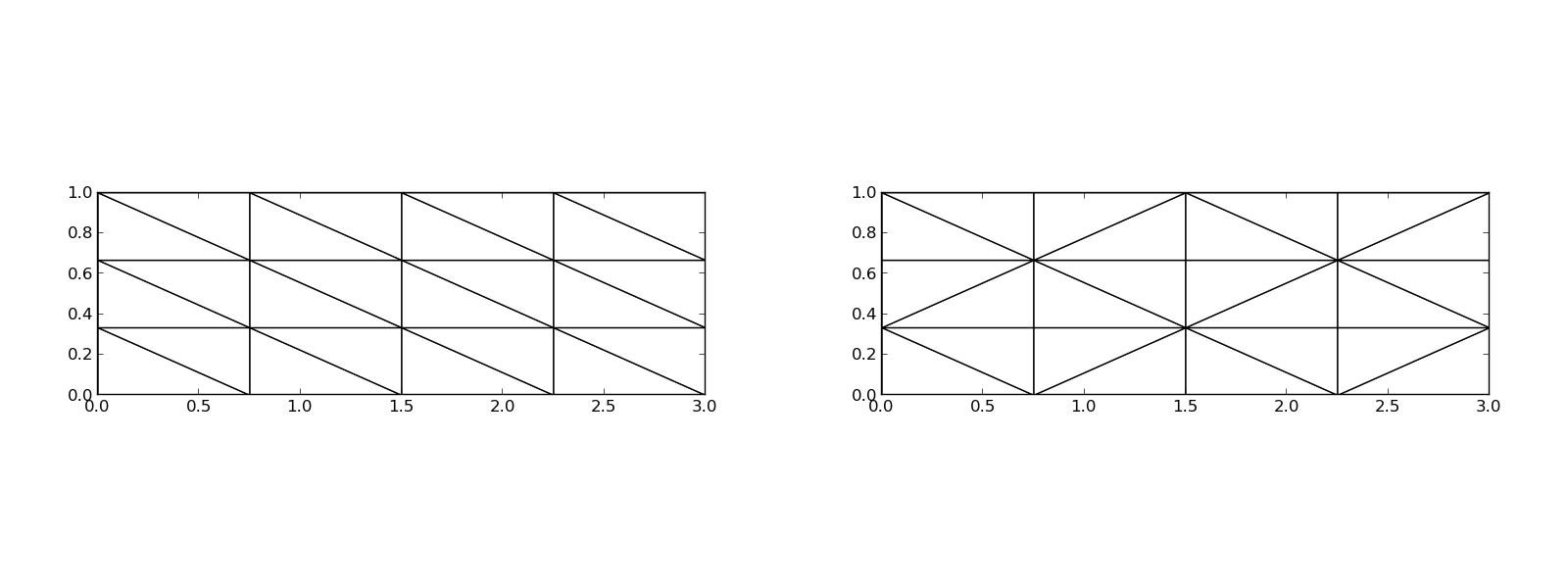
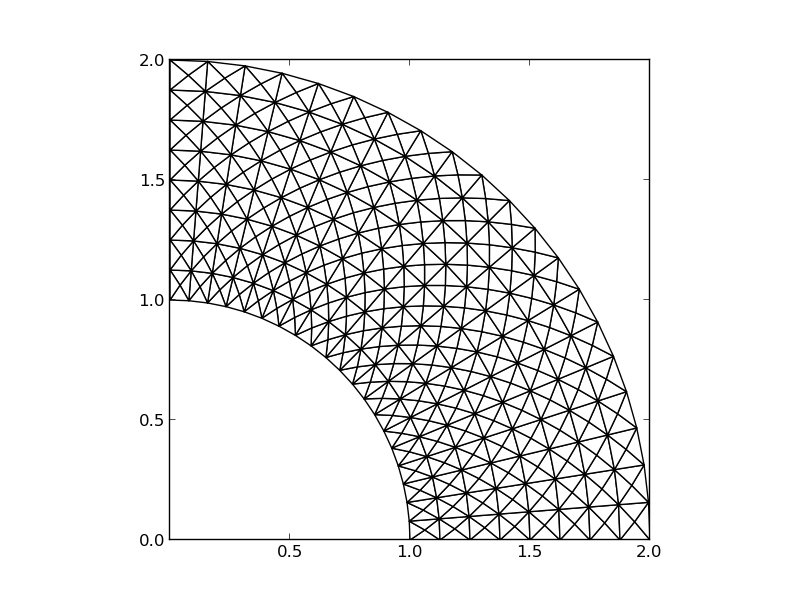
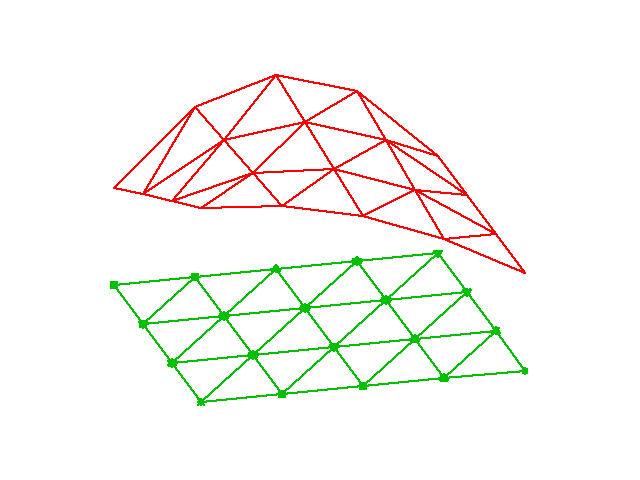
The P1 triangular 2D element: \( u \) is linear \( ax + by + c \) over each triangular cell

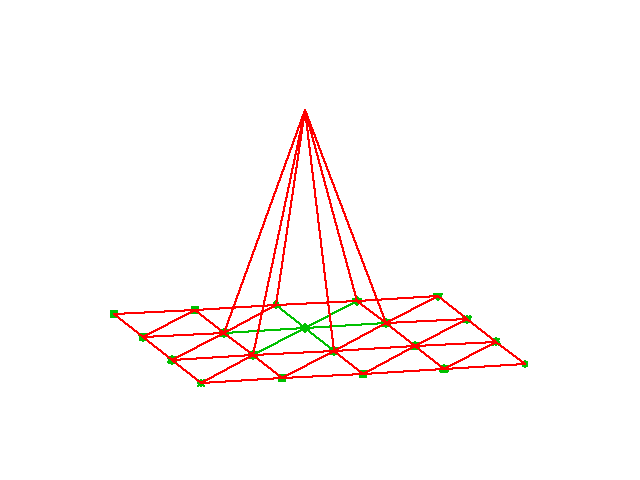

$$
\begin{align}
\refphi_0(X,Y) &= 1 - X - Y
\tag{30}\\
\refphi_1(X,Y) &= X
\tag{31}\\
\refphi_2(X,Y) &= Y
\tag{32}
\end{align}
$$
Higher-degree \( \refphi_r \) introduce more nodes (dof = node values)



Mapping of local \( \X = (X,Y) \) coordinates in the reference cell to global, physical \( \x = (x,y) \) coordinates:
$$
\begin{equation}
\x = \sum_{r} \refphi_r^{(1)}(\X)\xdno{q(e,r)}
\tag{33}
\end{equation}
$$
where
This mapping preserves the straight/planar faces and edges.

Idea: Use the basis functions of the element (not only the P1 functions) to map the element
$$
\x = \sum_{r} \refphi_r(\X)\xdno{q(e,r)}
$$
Advantage: higher-order polynomial basis functions now map the reference cell to a curved triangle or tetrahedron.

Integrals must be transformed from \( \Omega^{(e)} \) (physical cell) to \( \tilde\Omega^r \) (reference cell):
$$
\begin{align}
\int_{\Omega^{(e)}}\basphi_i (\x) \basphi_j (\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) \refphi_j (\X)
\det J\, \dX
\tag{34}\\
\int_{\Omega^{(e)}}\basphi_i (\x) f(\x) \dx &=
\int_{\tilde\Omega^r} \refphi_i (\X) f(\x(\X)) \det J\, \dX
\tag{35}
\end{align}
$$
where \( \dx = dx dy \) or \( \dx = dxdydz \) and \( \det J \) is the determinant of the
Jacobian of the mapping \( \x(\X) \).
$$
J = \left[\begin{array}{cc}
\frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y}\\
\frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y}
\end{array}\right], \quad
\det J = \frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}
- \frac{\partial x}{\partial Y}\frac{\partial y}{\partial X}
$$
Affine mapping (33): \( \det J=2\Delta \), \( \Delta = \hbox{cell volume} \)
Finite elements in 2D and 3D builds on the same ideas and concepts as in 1D, but there is simply much more to compute because the specific mathematical formulas in 2D and 3D are more complicated and the book keeping with dof maps also gets more complicated. The manual work is tedious, lengthy, and error-prone so automation by the computer is a must.