Study guide: Finite difference schemes for diffusion processes
Jul 14, 2016
The 1D diffusion equation
The famous diffusion equation, also known as the heat equation, reads
$$ \frac{\partial u}{\partial t} =
\dfc \frac{\partial^2 u}{\partial x^2}
$$
Here,
- \( u(x,t) \): unknown
- \( \dfc \): diffusion coefficient
Alternative, compact notation:
$$ u_t = \dfc u_{xx} $$
The initial-boundary value problem for 1D diffusion
$$
\begin{align}
\frac{\partial u}{\partial t} &=
\dfc \frac{\partial^2 u}{\partial x^2}, \quad x\in (0,L),\ t\in (0,T]
\tag{1}\\
u(x,0) &= I(x), \quad x\in [0,L]
\tag{2}\\
u(0,t) & = 0, \quad t>0,
\tag{3}\\
u(L,t) & = 0, \quad t>0\tp
\tag{4}
\end{align}
$$
Note:
- First-order derivative in time: one initial condition
- Second-order derivative in space: a boundary condition at each point of the boundary (2 points in 1D)
- Numerous applications throughout physics and biology
Step 1: Discretizing the domain
Mesh in time:
$$
\begin{equation}
0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T \tag{5}
\end{equation}
$$
Mesh in space:
$$
\begin{equation}
0 = x_0 < x_1 < x_2 < \cdots < x_{N_x-1} < x_{N_x} = L \tag{6}
\end{equation}
$$
Uniform mesh with constant mesh spacings \( \Delta t \) and \( \Delta x \):
$$
\begin{equation}
x_i = i\Delta x,\ i=0,\ldots,N_x,\quad
t_i = n\Delta t,\ n=0,\ldots,N_t
\tag{7}
\end{equation}
$$
The discrete solution
- The numerical solution is a mesh function: \( u_i^n \approx \uex(x_i,t_n) \)
- Finite difference stencil (or scheme): equation for \( u^n_i \) involving neighboring space-time points

Step 2: Fulfilling the equation at the mesh points
Require the PDE (1) to be fulfilled at an arbitrary interior mesh point \( (x_i,t_n) \) leads to
$$
\begin{equation}
\frac{\partial}{\partial t} u(x_i, t_n) =
\dfc\frac{\partial^2}{\partial x^2} u(x_i, t_n)
\tag{8}
\end{equation}
$$
Applies to all interior mesh points: \( i=1,\ldots,N_x-1 \) and \( n=1,\ldots,N_t-1 \)
For \( n=0 \) we have the initial conditions \( u=I(x) \) and \( u_t=0 \)
At the boundaries \( i=0,N_x \) we have the boundary condition \( u=0 \).
Step 3: Replacing derivatives by finite differences
Use a forward difference in time and a centered difference in space (Forward Euler scheme):
$$
\begin{equation}
[D_t^+ u = \dfc D_xD_x u]^n_i
\tag{9}
\end{equation}
$$
Written out,
$$
\begin{equation}
\frac{u^{n+1}_i-u^n_i}{\Delta t} = \dfc \frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2}
\tag{10}
\end{equation}
$$
Initial condition: \( u^0_i = I(x_i) \), \( i=0,1,\ldots,N_x \).
Step 4: Formulating a recursive algorithm
- Nature of the algorithm: compute \( u \) in space at \( t=\Delta t, 2\Delta t, 3\Delta t,... \)
- Two time levels are involved in the general discrete equation: \( n+1 \) and \( n \)
- \( u^n_i \) is already computed for \( i=0,\ldots,N_x \), and \( u^{n+1}_i \) is the unknown quantity
Solve the discretized PDE for the unknown \( u^{n+1}_i \):
$$
\begin{equation}
u^{n+1}_i = u^n_i + F\left(
u^{n}_{i+1} - 2u^n_i + u^n_{i-1}\right)
\tag{11}
\end{equation}
$$
where
$$ F = \dfc\frac{\Delta t}{\Delta x^2} $$
The mesh Fourier number
$$ F = \dfc\frac{\Delta t}{\Delta x^2} $$
There is only one parameter, \( F \), in the discrete model: \( F \) lumps mesh parameters \( \Delta t \) and \( \Delta x \) with the only physical parameter, the diffusion coefficient \( \dfc \). The value \( F \) and the smoothness of \( I(x) \) govern the quality of the numerical solution.
The finite difference stencil

The computational algorithm for the Forward Euler scheme
- compute \( u^0_i=I(x_i) \), \( i=0,\ldots,N_x \)
- for \( n=0,1,\ldots,N_t \):
- compute \( u^{n+1}_i \) from (11) for all the internal spatial points \( i=1,\ldots,N_x-1 \)
- set the boundary values \( u^{n+1}_i=0 \) for \( i=0 \) and \( i=N_x \)
We visit one mesh point \( (x_i,t_{n+1}) \) at a time, and we have an explicit formula for computing the associated \( u^{n+1}_i \) value. The spatial points can be updated in any sequence, but the time levels \( t_n \) must be updated in cronological order: \( t_n \) before \( t_{n+1} \).
The Python implementation of the computational algorithm
x = linspace(0, L, Nx+1) # mesh points in space
dx = x[1] - x[0]
t = linspace(0, T, Nt+1) # mesh points in time
dt = t[1] - t[0]
F = a*dt/dx**2
u = zeros(Nx+1)
u_1 = zeros(Nx+1)
# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
u_1[i] = I(x[i])
for n in range(0, Nt):
# Compute u at inner mesh points
for i in range(1, Nx):
u[i] = u_1[i] + F*(u_1[i-1] - 2*u_1[i] + u_1[i+1])
# Insert boundary conditions
u[0] = 0; u[Nx] = 0
# Update u_1 before next step
u_1[:]= u
# or more efficient switch of references
#u_1, u = u, u_1
Moving finite difference stencil
web page or a movie file.
Demo program
- Program: diffu1D_u0.py
- Produces animation on the screen
- Each frame stored in
tmp_frame%04d.pngfiles
tmp_frame0000.png,tmp_frame0001.png, ...
How to make movie file in modern formats:
Terminal> name=tmp_frame%04d.png
Terminal> fps=8 # frames per second in movie
Terminal> avconv -r $fps -i $name -vcodec flv movie.flv
Terminal> avconv -r $fps -i $name -vcodec libx64 movie.mp4
Terminal> avconv -r $fps -i $name -vcodec libvpx movie.webm
Terminal> avconv -r $fps -i $name -vcodec libtheora movie.ogg
Forward Euler applied to an initial plug profile
\( N_x=50 \). The method results in a growing, unstable solution if \( F>0.5 \).
|
Choosing \( F=0.5 \) gives a strange saw tooth-like curve.
|
Lowering \( F \) to 0.25 gives a smooth (expected) solution.
|
Forward Euler applied to a Gaussian profile
\( N_x=50 \). \( F=0.5 \).
|
|
|
Backward Euler scheme
Backward difference in time, centered difference in space:
$$
\begin{equation}
[D_t^- u = D_xD_x u]^n_i
\tag{12}
\end{equation}
$$
Written out:
$$
\begin{equation}
\frac{u^{n}_i-u^{n-1}_i}{\Delta t} = \dfc\frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2}
\tag{13}
\end{equation}
$$
Assumption: \( u^{n-1}_i \) is computed, but all quantities at the new time level \( t_n \) are unknown.
We cannot solve wrt \( u^n_i \) because that unknown value is coupled to two other unknown values: \( u^n_{i-1} \) and \( u^n_{i+1} \). That is, all the new unknown values are coupled to each other in a linear system of algebraic equations.
Let's write out the equations for \( N_x=3 \)
Equation (13) written for \( i=1,\ldots,Nx-1= 1,2 \) becomes
$$
\begin{align}
\frac{u^{n}_1-u^{n-1}_1}{\Delta t} &= \dfc\frac{u^{n}_{2} - 2u^n_1 + u^n_{0}}{\Delta x^2}
\tag{14}\\
\frac{u^{n}_2-u^{n-1}_2}{\Delta t} &= \dfc\frac{u^{n}_{3} - 2u^n_2 + u^n_{1}}{\Delta x^2}
\tag{15}
\end{align}
$$
(The boundary values \( u^n_0 \) and \( u^n_3 \) are known as zero.)
Collecting the unknown new values on the left-hand side and writing as \( 2\times 2 \) matrix system:
$$ \left(\begin{array}{cc}
1+ 2F & - F\\
- F & 1+ 2F
\end{array}\right)
\left(\begin{array}{c}
u^{n}_1\\
u^{n}_{2}\\
\end{array}\right)
=
\left(\begin{array}{c}
u^{n-1}_1\\
u^{n-1}_2
\end{array}\right)
$$
Two classes of discretization methods: explicit and implicit
Discretization methods that lead linear systems are known as implicit methods.
Discretization methods that avoid linear systems and have an explicit formula for each new value of the unknown are called explicit methods.
The linear system for a general \( N_x \)
$$
\begin{equation}
- F_o u^n_{i-1} + \left(1+ 2F_o \right) u^{n}_i - F_o u^n_{i+1} =
u_{i-1}^{n-1}
\tag{16}
\end{equation}
$$
for \( i=1,\ldots,Nx-1 \).
What are the unknowns in the linear system?
- either \( u^n_i \) for \( i=1,\ldots,N_x-1 \) (all internal spatial mesh points)
- or \( u^n_i \), \( i=0,\ldots,N_x \) (all spatial points)
The linear system in matrix notation:
$$
\begin{equation*} AU = b,\quad U=(u^n_0,\ldots,u^n_{N_x})
\end{equation*}
$$
\( A \) is very sparse: a tridiagonal matrix
$$
\begin{equation}
A =
\left(
\begin{array}{cccccccccc}
A_{0,0} & A_{0,1} & 0
&\cdots &
\cdots & \cdots & \cdots &
\cdots & 0 \\
A_{1,0} & A_{1,1} & 0 & \ddots & & & & & \vdots \\
0 & A_{2,1} & A_{2,2} & A_{2,3} &
\ddots & & & & \vdots \\
\vdots & \ddots & & \ddots & \ddots & 0 & & & \vdots \\
\vdots & & \ddots & \ddots & \ddots & \ddots & \ddots & & \vdots \\
\vdots & & & 0 & A_{i,i-1} & A_{i,i} & A_{i,i+1} & \ddots & \vdots \\
\vdots & & & & \ddots & \ddots & \ddots &\ddots & 0 \\
\vdots & & & & &\ddots & \ddots &\ddots & A_{N_x-1,N_x} \\
0 &\cdots & \cdots &\cdots & \cdots & \cdots & 0 & A_{N_x,N_x-1} & A_{N_x,N_x}
\end{array}
\right)
\tag{17}
\end{equation}
$$
Detailed expressions for the matrix entries
The nonzero elements are given by
$$
\begin{align}
A_{i,i-1} &= -F_o
\tag{18}\\
A_{i,i} &= 1+ 2F_o
\tag{19}\\
A_{i,i+1} &= -F_o
\tag{20}
\end{align}
$$
for \( i=1,\ldots,N_x-1 \).
The equations for the boundary points correspond to
$$
A_{0,0} = 1,\quad A_{0,1} = 0,\quad A_{N_x,N_x-1} = 0,\quad
A_{N_x,N_x} = 1
$$
The right-hand side
$$
\begin{equation}
b = \left(\begin{array}{c}
b_0\\
b_1\\
\vdots\\
b_i\\
\vdots\\
b_{N_x}
\end{array}\right)
\tag{21}
\end{equation}
$$
with
$$
\begin{align}
b_0 &= 0
\tag{22}\\
b_i &= u^{n-1}_i,\quad i=1,\ldots,N_x-1
\tag{23}\\
b_{N_x} &= 0
\tag{24}
\end{align}
$$
Naive Python implementation with a dense \( (N_x+1)\times(N_x+1) \) matrix
x = linspace(0, L, Nx+1) # mesh points in space
dx = x[1] - x[0]
t = linspace(0, T, N+1) # mesh points in time
u = zeros(Nx+1)
u_1 = zeros(Nx+1)
# Data structures for the linear system
A = zeros((Nx+1, Nx+1))
b = zeros(Nx+1)
for i in range(1, Nx):
A[i,i-1] = -F
A[i,i+1] = -F
A[i,i] = 1 + 2*F
A[0,0] = A[Nx,Nx] = 1
# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
u_1[i] = I(x[i])
import scipy.linalg
for n in range(0, Nt):
# Compute b and solve linear system
for i in range(1, Nx):
b[i] = -u_1[i]
b[0] = b[Nx] = 0
u[:] = scipy.linalg.solve(A, b)
# Update u_1 before next step
u_1, u = u, u_1
A sparse matrix representation will dramatically reduce the computational complexity
- With a dense matrix, the algorithm leads to \( \Oof{N_x^3} \) operations
- Utilizing the sparsity, the algorithm has complexity \( \Oof{N_x} \)!
-
scipy.sparseenables storage and calculations with the three nonzero diagonals only
# Representation of sparse matrix and right-hand side
diagonal = zeros(Nx+1)
lower = zeros(Nx)
upper = zeros(Nx)
b = zeros(Nx+1)
Computing the sparse matrix
# Precompute sparse matrix
diagonal[:] = 1 + 2*F
lower[:] = -F #1
upper[:] = -F #1
# Insert boundary conditions
diagonal[0] = 1
upper[0] = 0
diagonal[Nx] = 1
lower[-1] = 0
import scipy.sparse
A = scipy.sparse.diags(
diagonals=[main, lower, upper],
offsets=[0, -1, 1], shape=(Nx+1, Nx+1),
format='csr')
# Set initial condition
for i in range(0,Nx+1):
u_1[i] = I(x[i])
for n in range(0, Nt):
b = u_1
b[0] = b[-1] = 0.0 # boundary conditions
u[:] = scipy.sparse.linalg.spsolve(A, b)
# Switch variables before next step
u_1, u = u, u_1
Backward Euler applied to a plug profile
\( N_x=50 \). \( F=0.5 \).
Backward Euler applied to a Gaussian profile
\( N_x=50 \).
|
\( F=0.5 \).
|
\( F=5 \).
|
Crank-Nicolson scheme
The PDE is sampled at points \( (x_i,t_{n+\half}) \) (at the spatial mesh points, but in between two temporal mesh points).
$$
\frac{\partial}{\partial t} u(x_i, t_{n+\half}) =
\dfc\frac{\partial^2}{\partial x^2}u(x_i, t_{n+\half})
$$
for \( i=1,\ldots,N_x-1 \) and \( n=0,\ldots, N_t-1 \).
Centered differences in space and time:
$$ [D_t u = \dfc D_xD_x u]^{n+\half}_i$$
Averaging in time is necessary in the Crank-Nicolson scheme
Right-hand side term:
$$ \frac{1}{\Delta x^2}\left(u^{n+\half}_{i-1} - 2u^{n+\half}_i + u^{n+\half}_{i+1}\right)$$
Problem: \( u^{n+\half}_i \) is not one of the unknowns we compute.
Solution: replace \( u^{n+\half}_i \) by an arithmetic average:
$$ u^{n+\half}_i\approx
\half\left(u^{n}_i +u^{n+1}_{i}\right)
$$
In compact notation (arithmetic average in time \( \overline{u}^t \)):
$$ [D_t u = \dfc D_xD_x \overline{u}^t]^{n+\half}_i$$
Crank-Nicolsoon scheme written out
$$
\begin{equation}
u^{n+1}_i - \half F(u^{n+1}_{i-1} - 2u^{n+1}_i + u^{n+1}_{i+1})
= u^{n}_i + \half F(u^{n}_{i-1} - 2u^{n}_i + u^{n}_{i+1})
\tag{25}
\end{equation}
$$
Observe:
- The unknowns are \( u^{n+1}_{i-1}, u^{n+1}_{i}, u^{n+1}_{i+1} \)
- These unknowns are coupled to each other (in a linear system)
- Must solve \( AU=b \) at each time level
Now,
$$
\begin{align}
A_{i,i-1} &= -\half F_o
\tag{26}\\
A_{i,i} &= \half + F_o
\tag{27}\\
A_{i,i+1} &= -\half F_o
\tag{28}
\end{align}
$$
for internal points. For boundary points,
$$
\begin{align}
A_{0,0} &= 1
\tag{29}\\
A_{0,1} &= 0
\tag{30}\\
A_{N_x,N_x-1} &= 0
\tag{31}\\
A_{N_x,N_x} &= 1
\tag{32}
\end{align}
$$
Right-hand side:
$$
\begin{align}
b_0 &= 0
\tag{33}\\
b_i &= u^{n-1}_i,\quad i=1,\ldots,N_x-1
\tag{34}\\
b_{N_x} &= 0 \tag{35}
\end{align}
$$
Crank-Nicolson applied to a plug profile
Crank-Nicolson never blows up, so any \( F \) can be used (modulo loss of accuracy).
|
\( N_x=50 \).
\( F=5 \) gives instabilities.
|
\( N_x=50 \).
\( F=0.5 \) gives a smooth solution.
|
Crank-Nicolson applied to a Gaussian profile
\( N_x=50 \).
|
\( F=0.5 \).
|
\( F=5 \).
|
The \( \theta \) rule
The \( \theta \) rule condenses a family of finite difference approximations in time to one formula
- \( \theta=0 \) gives the Forward Euler scheme in time
- \( \theta=1 \) gives the Backward Euler scheme in time
- \( \theta=\half \) gives the Crank-Nicolson scheme in time
Applied to \( u_t=\dfc u_{xx} \):
$$ \frac{u^{n+1}_i-u^n_i}{\Delta t} =
\dfc\left( \theta \frac{u^{n+1}_{i+1} - 2u^{n+1}_i + u^{n+1}_{i-1}}{\Delta x^2}
+ (1-\theta) \frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2}\right)
$$
Matrix entries:
$$ A_{i,i-1} = -F_o\theta,\quad A_{i,i} = 1+2F_o\theta\quad,
A_{i,i+1} = -F_o\theta$$
Right-hand side:
$$ b_i = u^n_{i} + F_o(1-\theta)
\frac{u^{n}_{i+1} - 2u^n_i + u^n_{i-1}}{\Delta x^2}
$$
The Laplace and Poisson equation
Laplace equation:
$$ \nabla^2 u = 0,\quad \mbox{1D: } u''(x)=0$$
Poisson equation:
$$ -\nabla^2 u = f,\quad \mbox{1D: } -u''(x)=f(x)$$
These are limiting behavior of time-dependent diffusion equations if
$$ \lim_{t\rightarrow\infty}\frac{\partial u}{\partial t} = 0$$
Then \( u_t = \dfc u_{xx} + 0 \) in the limit \( t\rightarrow\infty \) reduces to
$$ u_{xx} + f = 0$$
We can solve 1D Poisson/Laplace equation by going to infinity in time-dependent diffusion equations
Looking at the numerical schemes, \( F\rightarrow\infty \) leads to the Laplace or Poisson equations (without \( f \) or with \( f \), resp.).
Good news: choose \( F \) large in the BE or CN schemes and one time step is enough to produce the stationary solution for \( t\rightarrow\infty \).
Extensions
These extensions are performed exactly as for a wave equation as they only affect the spatial derivatives (which are the same as in the wave equation).
- Variable coefficients
- Neumann and Robin conditions
- 2D and 3D
Future versions of this document will for completeness and independence of the wave equation document feature info on the three points. The Robin condition is new, but straightforward to handle:
$$ -\dfc\frac{\partial u}{\partial n} = h_T(u-U_s),\quad
[-\dfc D_x u = h_T(u-U_s)]^n_i
$$
Analysis of schemes for the diffusion equation
Properties of the solution
The PDE
$$
u_t = \dfc u_{xx}
$$
admits solutions
$$
u(x,t) = Qe^{-\dfc k^2 t}\sin\left( kx\right)
$$
Observations from this solution:
- The initial shape \( I(x)=Q\sin kx \) undergoes a damping \( \exp{(-\dfc k^2t)} \)
- The damping is very strong for short waves (large \( k \))
- The damping is weak for long waves (small \( k \))
- Consequence: \( u \) is smoothened with time
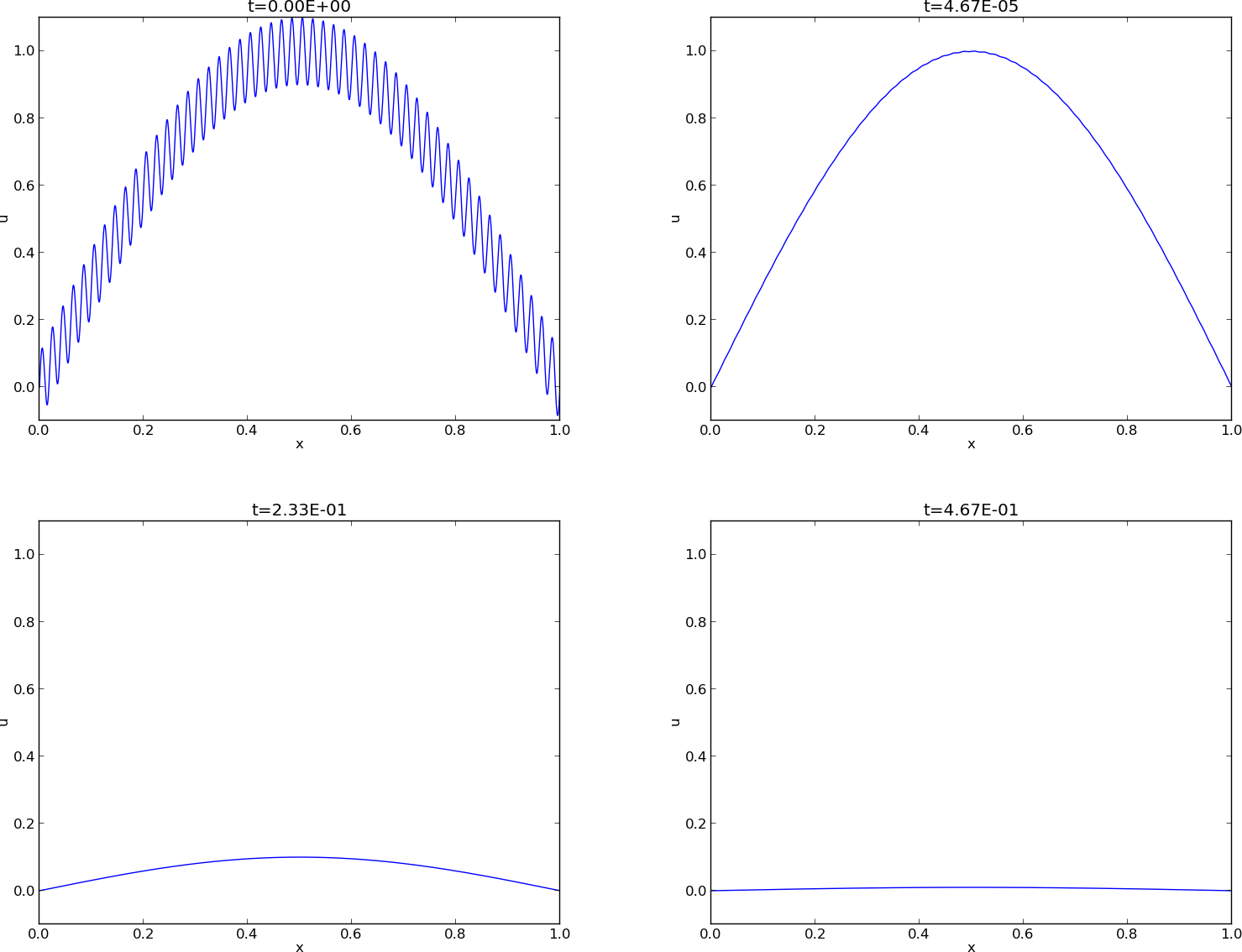
Example
Test problem:
$$
\begin{align*}
u_t &= u_{xx},\quad &x\in (0,1),\ t\in (0,T]\\
u(0,t) &= u(1,t) = 0,\quad &t\in (0,T]\\
u(x,0) & = \sin (\pi x) + 0.1\sin(100\pi x)
\end{align*}
$$
Exact solution:
$$
u(x,t) = e^{-\pi^2 t}\sin (\pi x) + 0.1e^{-\pi^2 10^4 t}\sin (100\pi x)
$$
High frequency components of the solution are very quickly damped
Damping of a discontinuity; problem
Two pieces of a material, at different temperatures, are brought in contact at \( t=0 \). Assume the end points of the pieces are kept at the initial temperature. How does the heat flow from the hot to the cold piece?
Or: A huge ion concentration on one side of a synapse in the brain (concentration discontinuity) is released and ions move by diffusion.
Damping of a discontinuity; model
Assume a 1D model is sufficient (e.g., insulated rod):
$$
u(x,0)=\left\lbrace
\begin{array}{ll}
U_L, & x < L/2\\
U_R,& x\geq L/2
\end{array}\right.
$$
$$ \frac{\partial u}{\partial t} = \dfc
\frac{\partial^2 u}{\partial x^2},\quad u(0,t)=U_L,\ u(L,t)=U_R$$
Damping of a discontinuity; Backward Euler scheme
Discrete model:
$$ [D_t^- u = \dfc D_xD_x]^n_i $$
results in a (tridiagonal) linear system
$$
- F u^n_{i-1} + \left(1+ 2F \right) u^{n}_i - F u^n_{i+1} =
u_{i-1}^{n-1}
$$
where
$$ F = \dfc\frac{\Delta t}{\Delta x^2} $$
is the mesh Fourier number
Damping of a discontinuity; Backward Euler simulation \( F=\half \)
Damping of a discontinuity; Forward Euler scheme
Discrete model:
$$ [D_t^+ u = \dfc D_xD_x]^n_i $$
results in the explicit updating formula
$$ u^{n+1}_i = u^n_i + F\left(
u^{n}_{i+1} - 2u^n_i + u^n_{i-1}\right)
$$
Damping of a discontinuity; Forward Euler simulation \( F=\half \)
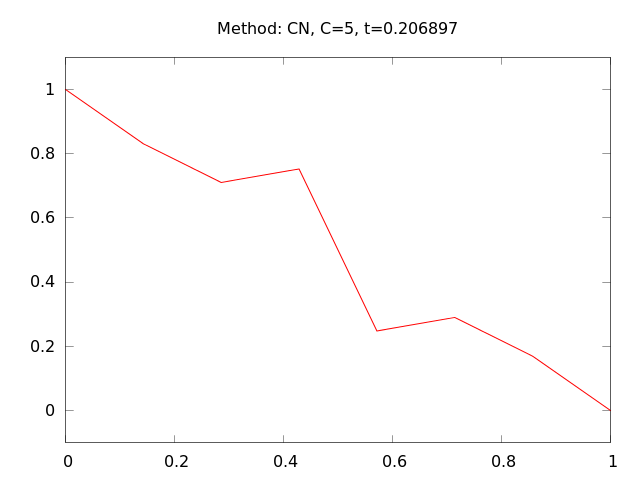
Damping of a discontinuity; Crank-Nicolson scheme
Discrete model:
$$ [D_t u = \dfc D_xD_x\overline{u}^t]^n_i $$
results in a tridiagonal linear system
Damping of a discontinuity; Crank-Nicolson simulation \( F=5 \)
Fourier representation
Represent \( I(x) \) as a Fourier series
$$
I(x) \approx \sum_{k\in K} b_k e^{ikx}
$$
The corresponding sum for \( u \) is
$$
u(x,t) \approx \sum_{k\in K} b_k e^{-\dfc k^2t}e^{ikx}
$$
Such solutions are also accepted by the numerical schemes, but with an amplification factor \( A \) different from \( \exp{({-\dfc k^2t})} \):
$$
u^n_q = A^n e^{ikq\Delta x} = A^ne^{ikx}
$$
Analysis of the finite difference schemes
Stability:
- \( |A| < 1 \): decaying numerical solutions (as we want)
- \( A < 0 \): oscillating numerical solutions (as we do not want)
Accuracy:
- Compare numerical and exact amplification factor: \( A \) vs \( \Aex = \exp{(-\dfc k^2 \Delta t)} \)
Analysis of the Forward Euler scheme
$$
\begin{equation*} [D_t^+ u = \dfc D_xD_x u]^n_q \end{equation*}
$$
Inserting
$$ u^n_q = A^n e^{ikq\Delta x}$$
leads to
$$
A = 1 -4F\sin^2\left(
\frac{k\Delta x}{2}\right),\quad
F = \frac{\dfc\Delta t}{\Delta x^2}\mbox{ (mesh Fourier number)}
$$
The complete numerical solution is
$$
u^n_q = (1 -4F\sin^2 p)^ne^{ikq\Delta x},\quad
p = k\Delta x/2
$$
Key spatial discretization quantity: the dimensionless \( p=\half k\Delta x \)
Results for stability
We always have \( A\leq 1 \). The condition \( A\geq -1 \) implies
$$ 4F\sin^2p\leq 2 $$
The worst case is when \( \sin^2 p=1 \), so a sufficient criterion for
stability is
$$ F\leq {\half} $$
or:
$$ \Delta t\leq \frac{\Delta x^2}{2\dfc} $$
Less favorable criterion than for \( u_{tt}=c^2u_{xx} \): halving \( \Delta x \) implies time step \( \frac{1}{4}\Delta t \) (not just \( \half\Delta t \) as in a wave equation). Need very small time steps for fine spatial meshes!
Analysis of the Backward Euler scheme
$$
\begin{equation*} [D_t^- u = \dfc D_xD_x u]^n_q\end{equation*}
$$
$$ u^n_q = A^n e^{ikq\Delta x}$$
$$ A = (1 + 4F\sin^2p)^{-1} $$
$$ u^n_q = (1 + 4F\sin^2p)^{-n}e^{ikq\Delta x} $$
Stability: We see that \( |A| < 1 \) for all \( \Delta t>0 \) and that \( A>0 \) (no oscillations)
Analysis of the Crank-Nicolson scheme
The scheme
$$ [D_t u = \dfc D_xD_x \overline{u}^x]^{n+\half}_q$$
leads to
$$ A = \frac{ 1 - 2F\sin^2p}{1 + 2F\sin^2p} $$
$$ u^n_q = \left(\frac{ 1 - 2F\sin^2p}{1 + 2F\sin^2p}\right)^ne^{ikp\Delta x}$$
Stability: The criteria \( A>-1 \) and \( A < 1 \) are fulfilled for any \( \Delta t >0 \)
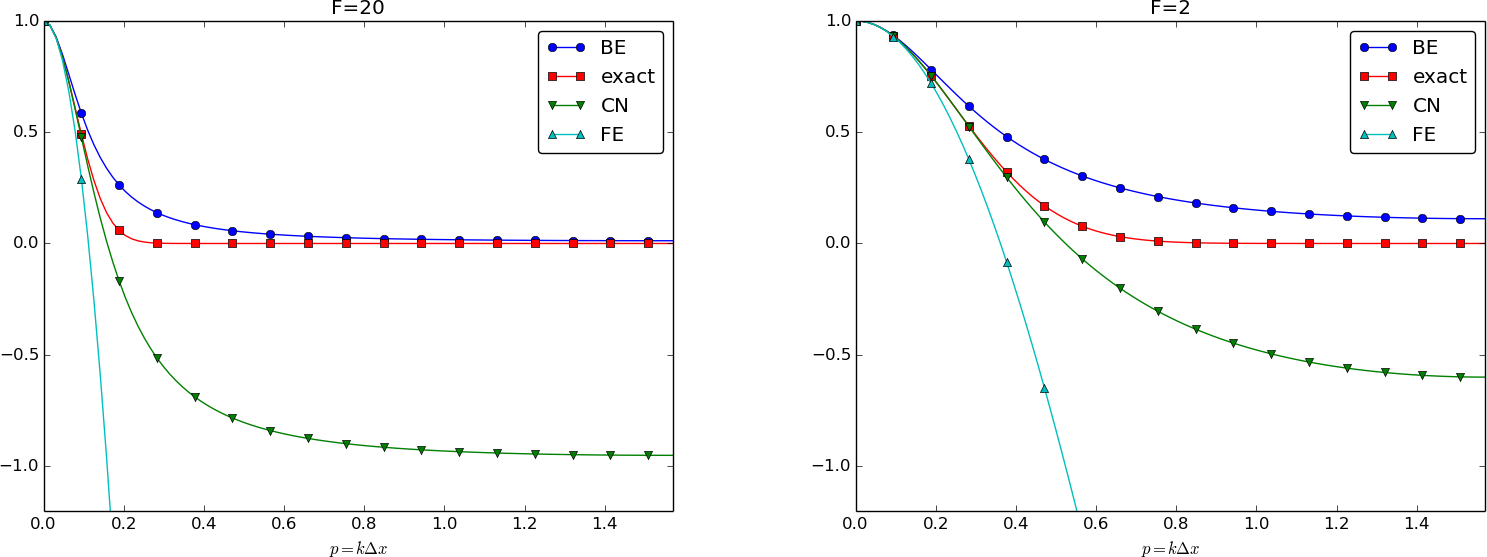
Summary of amplification factors
$$
\begin{align*}
\Aex &= \exp{(-\alpha k^2\Delta t)} = \exp{(-4Fp^2)}\\
A &= 1 -4F\sin^2\left(\frac{k\Delta x}{2}\right)\quad\mbox{Forward Euler}\\
A &= (1 + 4F\sin^2p)^{-1}\quad\mbox{Backward Euler}\\
A &= \frac{ 1 - 2F\sin^2p}{1 + 2F\sin^2p}\quad\mbox{Crank-Nicolson}
\end{align*}
$$
Note: \( \Aex = \exp{(-\dfc k^2\Delta t)}=\exp{(-F k^2\Delta x^2)}= \exp{(-F4p^2)} \).
Summary of accuracy of amplification factors; large time steps
Summary of accuracy of amplification factors; time steps around the Forward Euler stability limit

Summary of accuracy of amplification factors; small time steps
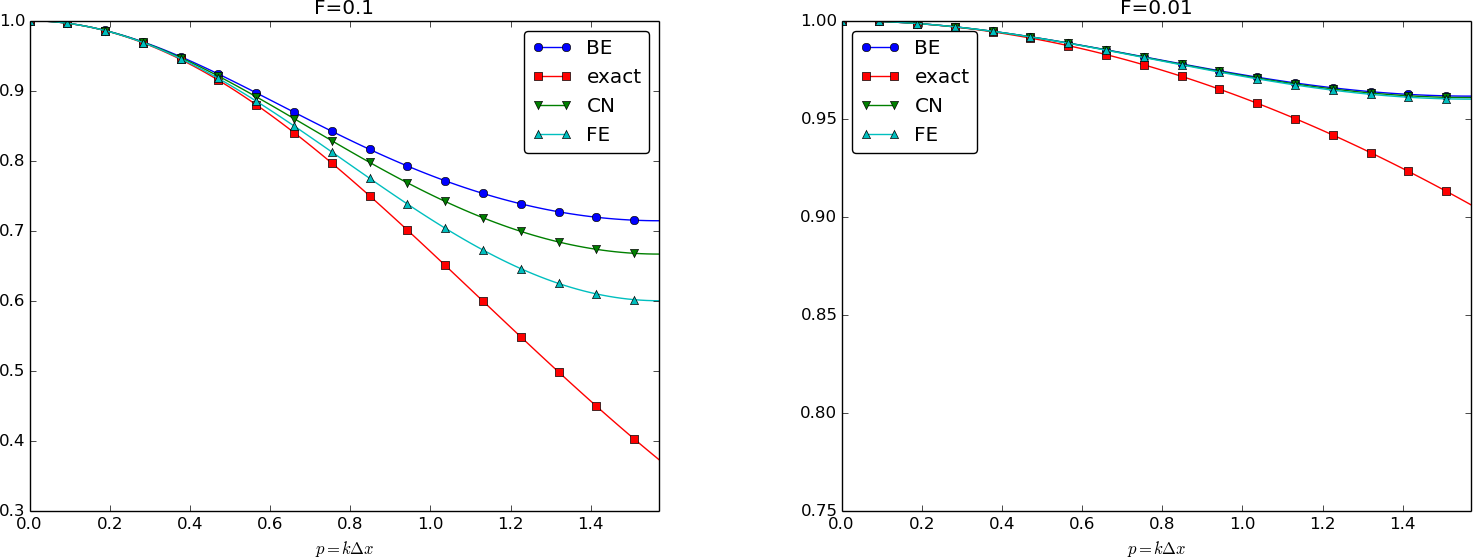
Observations
- The key spatial discretization parameter is the dimensionless \( p=\half k\Delta x \)
- The key temporal discretization parameter is the dimensionless \( F = \dfc\Delta t/\Delta x^2 \)
- Important: \( \Delta t \) and \( \Delta x \) in combination with \( \dfc \) and \( k \) determine accuracy
- Crank-Nicolson gives oscillations and not much damping of short waves for increasing \( F \)
- These waves will manifest themselves as high frequency oscillatory noise in the solution
- Steep solutions will have short waves with significant (visible) amplitudes
- All schemes fail to dampen short waves enough
The problems of correct damping for \( u_t = u_{xx} \) is partially manifested in the similar time discretization schemes for \( u'(t)=-\dfc u(t) \).