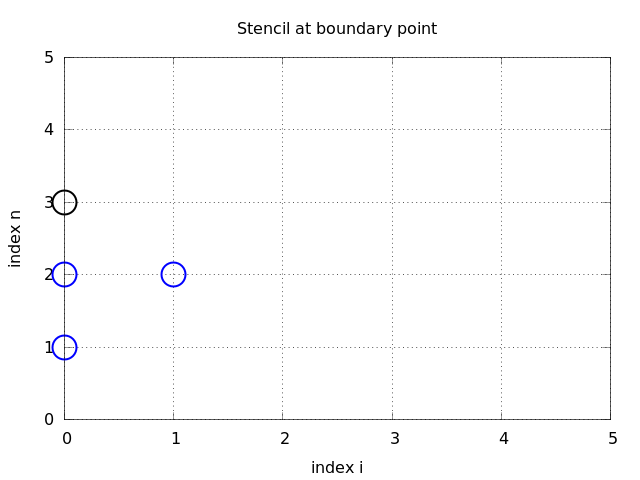
Figure 27: Modified stencil at a boundary with a Neumann condition.
The boundary condition \( u=0 \) in a wave equation reflects the wave, but \( u \) changes sign at the boundary, while the condition \( u_x=0 \) reflects the wave as a mirror and preserves the sign, see a web page or a movie file for demonstration.
Our next task is to explain how to implement the boundary condition \( u_x=0 \), which is more complicated to express numerically and also to implement than a given value of \( u \). We shall present two methods for implementing \( u_x=0 \) in a finite difference scheme, one based on deriving a modified stencil at the boundary, and another one based on extending the mesh with ghost cells and ghost points.
When a wave hits a boundary and is to be reflected back, one applies the condition $$ \begin{equation} \frac{\partial u}{\partial n} \equiv \normalvec\cdot\nabla u = 0 \tag{194} \tp \end{equation} $$ The derivative \( \partial /\partial n \) is in the outward normal direction from a general boundary. For a 1D domain \( [0,L] \), we have that $$ \left.\frac{\partial}{\partial n}\right\vert_{x=L} = \left.\frac{\partial}{\partial x}\right\vert_{x=L},\quad \left.\frac{\partial}{\partial n}\right\vert_{x=0} = - \left.\frac{\partial}{\partial x}\right\vert_{x=0}\tp $$
Boundary conditions that specify the value of \( \partial u/\partial n \) (or shorter \( u_n \)) are known as Neumann conditions, while Dirichlet conditions refer to specifications of \( u \). When the values are zero (\( \partial u/\partial n=0 \) or \( u=0 \)) we speak about homogeneous Neumann or Dirichlet conditions.
How can we incorporate the condition (194) in the finite difference scheme? Since we have used central differences in all the other approximations to derivatives in the scheme, it is tempting to implement (194) at \( x=0 \) and \( t=t_n \) by the difference $$ \begin{equation} [D_{2x} u]^n_0 = \frac{u_{-1}^n - u_n^n}{2\Delta x} = 0 \tp \tag{195} \end{equation} $$ The problem is that \( u_{-1}^n \) is not a \( u \) value that is being computed since the point is outside the mesh. However, if we combine (195) with the scheme for \( i=0 \), $$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right), \tag{196} \end{equation} $$ we can eliminate the fictitious value \( u_{-1}^n \). We see that \( u_{-1}^n=u_n^n \) from (195), which can be used in (196) to arrive at a modified scheme for the boundary point \( u_0^{n+1} \): $$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + 2C^2 \left(u^{n}_{i+1}-u^{n}_{i}\right),\quad i=0 \tp \tag{197} \end{equation} $$ Figure 27 visualizes this equation for computing \( u^3_0 \) in terms of \( u^2_0 \), \( u^1_0 \), and \( u^2_1 \).
Figure 27: Modified stencil at a boundary with a Neumann condition.

Similarly, (194) applied at \( x=L \) is discretized by a central difference $$ \begin{equation} \frac{u_{N_x+1}^n - u_{N_x-1}^n}{2\Delta x} = 0 \tp \tag{198} \end{equation} $$ Combined with the scheme for \( i=N_x \) we get a modified scheme for the boundary value \( u_{N_x}^{n+1} \): $$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + 2C^2 \left(u^{n}_{i-1}-u^{n}_{i}\right),\quad i=N_x \tp \tag{199} \end{equation} $$
The modification of the scheme at the boundary is also required for the special formula for the first time step. How the stencil moves through the mesh and is modified at the boundary can be illustrated by an animation in a web page or a movie file.
We have seen in the preceding section
that the special formulas for the boundary points
arise from replacing \( u_{i-1}^n \) by \( u_{i+1}^n \) when computing
\( u_i^{n+1} \) from the stencil formula for \( i=0 \). Similarly, we
replace \( u_{i+1}^n \) by \( u_{i-1}^n \) in the stencil formula
for \( i=N_x \). This observation can conveniently
be used in the coding: we just work with the general stencil formula,
but write the code such that it is easy to replace u[i-1] by
u[i+1] and vice versa. This is achieved by
having the indices i+1 and i-1 as variables ip1 (i plus 1)
and im1 (i minus 1), respectively.
At the boundary we can easily define im1=i+1 while we use
im1=i-1 in the internal parts of the mesh. Here are the details
of the implementation (note that the updating formula for u[i]
is the general stencil formula):
i = 0
ip1 = i+1
im1 = ip1 # i-1 -> i+1
u[i] = u_n[i] + C2*(u_n[im1] - 2*u_n[i] + u_n[ip1])
i = Nx
im1 = i-1
ip1 = im1 # i+1 -> i-1
u[i] = u_n[i] + C2*(u_n[im1] - 2*u_n[i] + u_n[ip1])
We can in fact create one loop over both the internal and boundary points and use only one updating formula:
for i in range(0, Nx+1):
ip1 = i+1 if i < Nx else i-1
im1 = i-1 if i > 0 else i+1
u[i] = u_n[i] + C2*(u_n[im1] - 2*u_n[i] + u_n[ip1])
The program wave1D_n0.py contains a complete implementation of the 1D wave equation with boundary conditions \( u_x = 0 \) at \( x=0 \) and \( x=L \).
It would be nice to modify the test_quadratic test case from the
wave1D_u0.py with Dirichlet conditions, described in the section Verification. However, the Neumann
conditions require the polynomial variation in the \( x \) direction to
be of third degree, which causes challenging problems when
designing a test where the numerical solution is known exactly.
Exercise 2.15: Verification by a cubic polynomial in space outlines ideas and code
for this purpose. The only test in wave1D_n0.py is to start
with a plug wave at rest and see that the initial condition is
reached again perfectly after one period of motion, but such
a test requires \( C=1 \) (so the numerical solution coincides with
the exact solution of the PDE, see the section Numerical dispersion relation).
To improve our mathematical writing and our implementations, it is wise to introduce a special notation for index sets. This means that we write \( x_i \), followed by \( i\in\Ix \), instead of \( i=0,\ldots,N_x \). Obviously, \( \Ix \) must be the index set \( \Ix =\{0,\ldots,N_x\} \), but it is often advantageous to have a symbol for this set rather than specifying all its elements (all the time, as we have done up to now). This new notation saves writing and makes specifications of algorithms and their implementation as computer code simpler.
The first index in the set will be denoted \( \setb{\Ix} \) and the last \( \sete{\Ix} \). When we need to skip the first element of the set, we use \( \setr{\Ix} \) for the remaining subset \( \setr{\Ix}=\{1,\ldots,N_x\} \). Similarly, if the last element is to be dropped, we write \( \setl{\Ix}=\{0,\ldots,N_x-1\} \) for the remaining indices. All the indices corresponding to inner grid points are specified by \( \seti{\Ix}=\{1,\ldots,N_x-1\} \). For the time domain we find it natural to explicitly use 0 as the first index, so we will usually write \( n=0 \) and \( t_0 \) rather than \( n=\It^0 \). We also avoid notation like \( x_{\sete{\Ix}} \) and will instead use \( x_i \), \( i=\sete{\Ix} \).
The Python code associated with index sets applies the following conventions:
| Notation | Python |
|---|---|
| \( \Ix \) | Ix |
| \( \setb{\Ix} \) | Ix[0] |
| \( \sete{\Ix} \) | Ix[-1] |
| \( \setl{\Ix} \) | Ix[:-1] |
| \( \setr{\Ix} \) | Ix[1:] |
| \( \seti{\Ix} \) | Ix[1:-1] |
An important feature of the index set notation is that it
keeps our formulas and code independent of how
we count mesh points. For example, the notation \( i\in\Ix \) or \( i=\setb{\Ix} \)
remains the same whether \( \Ix \) is defined as above or as starting at 1,
i.e., \( \Ix=\{1,\ldots,Q\} \). Similarly, we can in the code define
Ix=range(Nx+1) or Ix=range(1,Q), and expressions
like Ix[0] and Ix[1:-1] remain correct. One application where
the index set notation is convenient is
conversion of code from a language where arrays has base index 0 (e.g.,
Python and C) to languages where the base index is 1 (e.g., MATLAB and
Fortran). Another important application is implementation of
Neumann conditions via ghost points (see next section).
For the current problem setting in the \( x,t \) plane, we work with the index sets $$ \begin{equation} \Ix = \{0,\ldots,N_x\},\quad \It = \{0,\ldots,N_t\}, \tag{200} \end{equation} $$ defined in Python as
Ix = range(0, Nx+1)
It = range(0, Nt+1)
A finite difference scheme can with the index set notation be specified as $$ \begin{align*} u_i^{n+1} &= u^n_i - \half C^2\left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right),\quad, i\in\seti{\Ix},\ n=0,\\ u^{n+1}_i &= -u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i}+u^{n}_{i-1}\right), \quad i\in\seti{\Ix},\ n\in\seti{\It},\\ u_i^{n+1} &= 0, \quad i=\setb{\Ix},\ n\in\setl{\It},\\ u_i^{n+1} &= 0, \quad i=\sete{\Ix},\ n\in\setl{\It}\tp \end{align*} $$ The corresponding implementation becomes
# Initial condition
for i in Ix[1:-1]:
u[i] = u_n[i] - 0.5*C2*(u_n[i-1] - 2*u_n[i] + u_n[i+1])
# Time loop
for n in It[1:-1]:
# Compute internal points
for i in Ix[1:-1]:
u[i] = - u_nm1[i] + 2*u_n[i] + \
C2*(u_n[i-1] - 2*u_n[i] + u_n[i+1])
# Compute boundary conditions
i = Ix[0]; u[i] = 0
i = Ix[-1]; u[i] = 0
The program wave1D_dn.py applies the index set notation and solves the 1D wave equation \( u_{tt}=c^2u_{xx}+f(x,t) \) with quite general boundary and initial conditions:
How can we test that the Neumann conditions are correctly implemented?
The solver function in the wave1D_dn.py program described in the
box above accepts Dirichlet or Neumann conditions at \( x=0 \) and \( x=L \).
It is tempting to apply a quadratic solution as described in
the sections A slightly generalized model problem and Verification: exact quadratic solution,
but it turns out that this solution is no longer an exact solution
of the discrete equations if a Neumann condition is implemented on
the boundary. A linear solution does not help since we only have
homogeneous Neumann conditions in wave1D_dn.py, and we are
consequently left with testing just a constant solution: \( u=\hbox{const} \).
def test_constant():
"""
Check the scalar and vectorized versions for
a constant u(x,t). We simulate in [0, L] and apply
Neumann and Dirichlet conditions at both ends.
"""
u_const = 0.45
u_exact = lambda x, t: u_const
I = lambda x: u_exact(x, 0)
V = lambda x: 0
f = lambda x, t: 0
def assert_no_error(u, x, t, n):
u_e = u_exact(x, t[n])
diff = np.abs(u - u_e).max()
msg = 'diff=%E, t_%d=%g' % (diff, n, t[n])
tol = 1E-13
assert diff < tol, msg
for U_0 in (None, lambda t: u_const):
for U_L in (None, lambda t: u_const):
L = 2.5
c = 1.5
C = 0.75
Nx = 3 # Very coarse mesh for this exact test
dt = C*(L/Nx)/c
T = 18 # long time integration
solver(I, V, f, c, U_0, U_L, L, dt, C, T,
user_action=assert_no_error,
version='scalar')
solver(I, V, f, c, U_0, U_L, L, dt, C, T,
user_action=assert_no_error,
version='vectorized')
print U_0, U_L
Another test may utilize the fact that the approximation error vanishes when the Courant number is unity. We can, for example, start with a plug profile as initial condition, let this wave split into two plug waves, one in each direction, and check that the two plug waves come back and form the initial condition again after "one period" of the solution process. Neumann conditions can be applied at both ends. A proper test function reads
def test_plug():
"""Check that an initial plug is correct back after one period."""
L = 1.0
c = 0.5
dt = (L/10)/c # Nx=10
I = lambda x: 0 if abs(x-L/2.0) > 0.1 else 1
u_s, x, t, cpu = solver(
I=I,
V=None, f=None, c=0.5, U_0=None, U_L=None, L=L,
dt=dt, C=1, T=4, user_action=None, version='scalar')
u_v, x, t, cpu = solver(
I=I,
V=None, f=None, c=0.5, U_0=None, U_L=None, L=L,
dt=dt, C=1, T=4, user_action=None, version='vectorized')
tol = 1E-13
diff = abs(u_s - u_v).max()
assert diff < tol
u_0 = np.array([I(x_) for x_ in x])
diff = np.abs(u_s - u_0).max()
assert diff < tol
Other tests must rely on an unknown approximation error, so effectively we are left with tests on the convergence rate.
Instead of modifying the scheme at the boundary, we can introduce extra points outside the domain such that the fictitious values \( u_{-1}^n \) and \( u_{N_x+1}^n \) are defined in the mesh. Adding the intervals \( [-\Delta x,0] \) and \( [L, L+\Delta x] \), known as ghost cells, to the mesh gives us all the needed mesh points, corresponding to \( i=-1,0,\ldots,N_x,N_x+1 \). The extra points with \( i=-1 \) and \( i=N_x+1 \) are known as ghost points, and values at these points, \( u_{-1}^n \) and \( u_{N_x+1}^n \), are called ghost values.
The important idea is to ensure that we always have $$ u_{-1}^n = u_{1}^n\hbox{ and } u_{N_x+1}^n = u_{N_x-1}^n,$$ because then the application of the standard scheme at a boundary point \( i=0 \) or \( i=N_x \) will be correct and guarantee that the solution is compatible with the boundary condition \( u_x=0 \).
Some readers may find it strange to just extend the domain with ghost cells as a general technique, because in some problems there is a completely different medium with different physics and equations right outside of a boundary. Nevertheless, one should view the ghost cell technique as a purely mathematical technique, which is valid in the limit \( \Delta xrightarrow 0 \) and helps us to implement derivatives.
The u array now needs extra elements corresponding to the ghost
points. Two new point values are needed:
u = zeros(Nx+3)
u_n and u_nm1 must be defined accordingly.
Unfortunately, a major indexing problem arises with ghost cells.
The reason is that Python indices must start
at 0 and u[-1] will always mean the last element in u.
This fact gives, apparently, a mismatch between the mathematical
indices \( i=-1,0,\ldots,N_x+1 \) and the Python indices running over
u: 0,..,Nx+2. One remedy is to change the mathematical indexing
of \( i \) in the scheme and write
$$ u^{n+1}_i = \cdots,\quad i=1,\ldots,N_x+1,$$
instead of \( i=0,\ldots,N_x \) as we have previously used. The ghost
points now correspond to \( i=0 \) and \( i=N_x+1 \).
A better solution is to use the ideas of the section Index set notation:
we hide the specific index value in an index set and operate with
inner and boundary points using the index set notation.
To this end, we define u with proper length and Ix to be the corresponding
indices for the real physical mesh points (\( 1,2,\ldots,N_x+1 \)):
u = zeros(Nx+3)
Ix = range(1, u.shape[0]-1)
Ix[0] and Ix[-1] (as before).
We first update the solution at all physical mesh points (i.e., interior
points in the mesh):
for i in Ix:
u[i] = - u_nm1[i] + 2*u_n[i] + \
C2*(u_n[i-1] - 2*u_n[i] + u_n[i+1])
V(x) and f(x, t), as we must remember that the appropriate
\( x \) coordinate is given as x[i-Ix[0]]:
for i in Ix:
u[i] = u_n[i] + dt*V(x[i-Ix[0]]) + \
0.5*C2*(u_n[i-1] - 2*u_n[i] + u_n[i+1]) + \
0.5*dt2*f(x[i-Ix[0]], t[0])
It remains to update the solution at ghost points, i.e, u[0]
and u[-1] (or u[Nx+2]). For a boundary condition \( u_x=0 \),
the ghost value must equal the value at the associated inner mesh
point. Computer code makes this statement precise:
i = Ix[0] # x=0 boundary
u[i-1] = u[i+1]
i = Ix[-1] # x=L boundary
u[i+1] = u[i-1]
The physical solution to be plotted is now in u[1:-1], or
equivalently u[Ix[0]:Ix[-1]+1], so this slice is
the quantity to be returned from a solver function.
A complete implementation appears in the program
wave1D_n0_ghost.py.
We have to be careful with how the spatial and temporal mesh
points are stored. Say we let x be the physical mesh points,
x = linspace(0, L, Nx+1)
for i in Ix:
u_n[i] = I(x[i])
u_n and x have different lengths and the index i
corresponds to two different mesh points. In fact, x[i] corresponds
to u[1+i]. A correct implementation is
for i in Ix:
u_n[i] = I(x[i-Ix[0]])
f(x[i], t[n]) is incorrect
if x is defined to be the physical points, so x[i] must be
replaced by x[i-Ix[0]].
An alternative remedy is to let x also cover the ghost points such that
u[i] is the value at x[i].
The ghost cell is only added to the boundary where we have a Neumann condition. Suppose we have a Dirichlet condition at \( x=L \) and a homogeneous Neumann condition at \( x=0 \). One ghost cell \( [-\Delta x,0] \) is added to the mesh, so the index set for the physical points becomes \( \{1,\ldots,N_x+1\} \). A relevant implementation is
u = zeros(Nx+2)
Ix = range(1, u.shape[0])
...
for i in Ix[:-1]:
u[i] = - u_nm1[i] + 2*u_n[i] + \
C2*(u_n[i-1] - 2*u_n[i] + u_n[i+1]) + \
dt2*f(x[i-Ix[0]], t[n])
i = Ix[-1]
u[i] = U_0 # set Dirichlet value
i = Ix[0]
u[i-1] = u[i+1] # update ghost value
u[1:]
or (as always) u[Ix[0]:Ix[-1]+1].
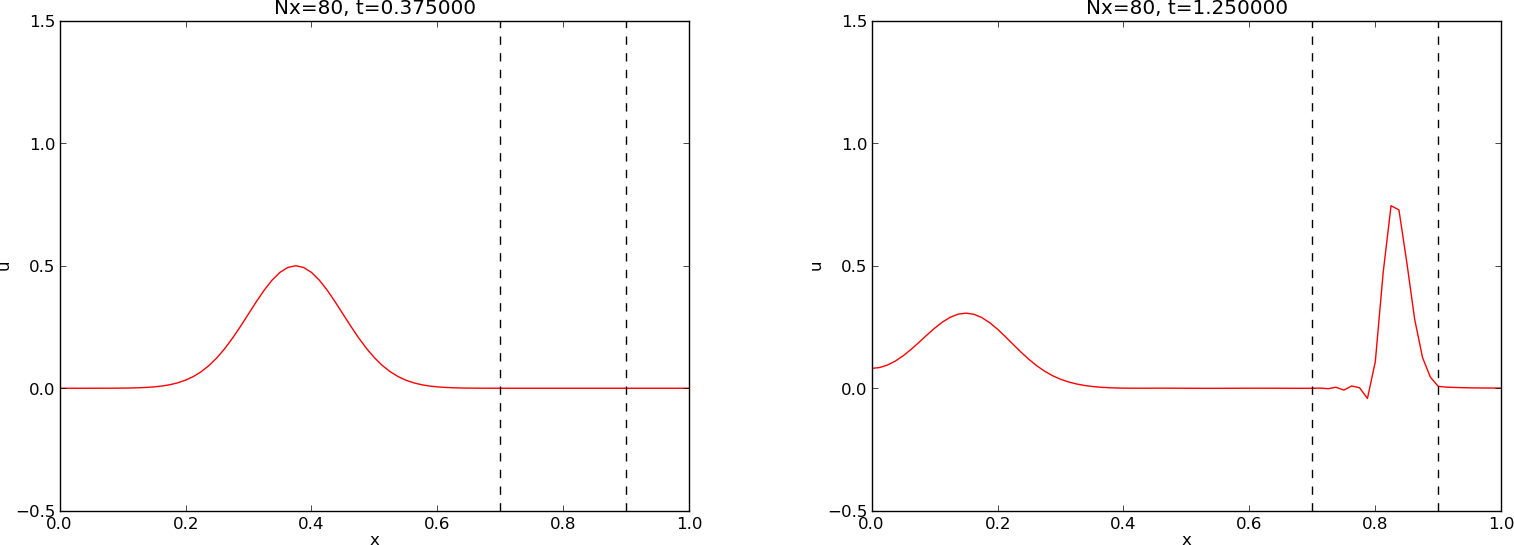
Our next generalization of the 1D wave equation (160) or (176) is to allow for a variable wave velocity \( c \): \( c=c(x) \), usually motivated by wave motion in a domain composed of different physical media. When the media differ in physical properties like density or porosity, the wave velocity \( c \) is affected and will depend on the position in space. Figure 28 shows a wave propagating in one medium \( [0, 0.7]\cup [0.9,1] \) with wave velocity \( c_1 \) (left) before it enters a second medium \( (0.7,0.9) \) with wave velocity \( c_2 \) (right). When the wave passes the boundary where \( c \) jumps from \( c_1 \) to \( c_2 \), a part of the wave is reflected back into the first medium (the reflected wave), while one part is transmitted through the second medium (the transmitted wave).
Figure 28: Left: wave entering another medium; right: transmitted and reflected wave.
Instead of working with the squared quantity \( c^2(x) \), we shall for notational convenience introduce \( q(x) = c^2(x) \). A 1D wave equation with variable wave velocity often takes the form $$ \begin{equation} \frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) + f(x,t) \tag{201} \tp \end{equation} $$ This is the most frequent form of a wave equation with variable wave velocity, but other forms also appear, see the section Waves on a string and equation (280).
As usual, we sample (201) at a mesh point, $$ \frac{\partial^2 }{\partial t^2} u(x_i,t_n) = \frac{\partial}{\partial x}\left( q(x_i) \frac{\partial}{\partial x} u(x_i,t_n)\right) + f(x_i,t_n), $$ where the only new term to discretize is $$ \frac{\partial}{\partial x}\left( q(x_i) \frac{\partial}{\partial x} u(x_i,t_n)\right) = \left[ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right)\right]^n_i \tp $$
The principal idea is to first discretize the outer derivative. Define $$ \phi = q(x) \frac{\partial u}{\partial x}, $$ and use a centered derivative around \( x=x_i \) for the derivative of \( \phi \): $$ \left[\frac{\partial\phi}{\partial x}\right]^n_i \approx \frac{\phi_{i+\half} - \phi_{i-\half}}{\Delta x} = [D_x\phi]^n_i \tp $$ Then discretize $$ \phi_{i+\half} = q_{i+\half} \left[\frac{\partial u}{\partial x}\right]^n_{i+\half} \approx q_{i+\half} \frac{u^n_{i+1} - u^n_{i}}{\Delta x} = [q D_x u]_{i+\half}^n \tp $$ Similarly, $$ \phi_{i-\half} = q_{i-\half} \left[\frac{\partial u}{\partial x}\right]^n_{i-\half} \approx q_{i-\half} \frac{u^n_{i} - u^n_{i-1}}{\Delta x} = [q D_x u]_{i-\half}^n \tp $$ These intermediate results are now combined to $$ \begin{equation} \left[ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right)\right]^n_i \approx \frac{1}{\Delta x^2} \left( q_{i+\half} \left({u^n_{i+1} - u^n_{i}}\right) - q_{i-\half} \left({u^n_{i} - u^n_{i-1}}\right)\right) \tag{202} \tp \end{equation} $$ With operator notation we can write the discretization as $$ \begin{equation} \left[ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right)\right]^n_i \approx [D_x (\overline{q}^{x} D_x u)]^n_i \tag{203} \tp \end{equation} $$
Many are tempted to use the chain rule on the term \( \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) \), but this is not a good idea when discretizing such a term.
The term with a variable coefficient expresses the net flux \( qu_x \) into a small volume (i.e., interval in 1D): $$ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) \approx \frac{1}{\Delta x}(q(x+\Delta x)u_x(x+\Delta x) - q(x)u_x(x))\tp$$ Our discretization reflects this principle directly: \( qu_x \) at the right end of the cell minus \( qu_x \) at the left end, because this follows from the formula (202) or \( [D_x(q D_x u)]^n_i \).
When using the chain rule, we get two terms \( qu_{xx} + q_xu_x \). The typical discretization is $$ \begin{equation} D_x q D_x u + D_{2x}q D_{2x} u]_i^n, \tag{204} \end{equation} $$ Writing this out shows that it is different from \( [D_x(q D_x u)]^n_i \) and lacks the physical interpretation of net flux into a cell. With a smooth and slowly varying \( q(x) \) the differences between the two discretizations are not substantial. However, when \( q \) exhibits (potentially large) jumps, \( [D_x(q D_x u)]^n_i \) with harmonic averaging of \( q \) yields a better solution than arithmetic averaging or (204). In the literature, the discretization \( [D_x(q D_x u)]^n_i \) totally dominates and very few mention the possibility of (204).
If \( q \) is a known function of \( x \), we can easily evaluate \( q_{i+\half} \) simply as \( q(x_{i+\half}) \) with \( x_{i+\half} = x_i + \half\Delta x \). However, in many cases \( c \), and hence \( q \), is only known as a discrete function, often at the mesh points \( x_i \). Evaluating \( q \) between two mesh points \( x_i \) and \( x_{i+1} \) must then be done by interpolation techniques, of which three are of particular interest in this context: $$ \begin{alignat}{2} q_{i+\half} &\approx \half\left( q_{i} + q_{i+1}\right) = [\overline{q}^{x}]_i \quad &\hbox{(arithmetic mean)} \tag{205}\\ q_{i+\half} &\approx 2\left( \frac{1}{q_{i}} + \frac{1}{q_{i+1}}\right)^{-1} \quad &\hbox{(harmonic mean)} \tag{206}\\ q_{i+\half} &\approx \left(q_{i}q_{i+1}\right)^{1/2} \quad &\hbox{(geometric mean)} \tag{207} \end{alignat} $$ The arithmetic mean in (205) is by far the most commonly used averaging technique and is well suited for smooth \( q(x) \) functions. The harmonic mean is often preferred when \( q(x) \) exhibits large jumps (which is typical for geological media). The geometric mean is less used, but popular in discretizations to linearize quadratic nonlinearities (see the section A centered scheme for quadratic damping for an example).
With the operator notation from (205) we can specify the discretization of the complete variable-coefficient wave equation in a compact way: $$ \begin{equation} \lbrack D_tD_t u = D_x\overline{q}^{x}D_x u + f\rbrack^{n}_i \tp \tag{208} \end{equation} $$ Strictly speaking, \( \lbrack D_x\overline{q}^{x}D_x u\rbrack^{n}_i = \lbrack D_x (\overline{q}^{x}D_x u)\rbrack^{n}_i \).
From the compact difference notation we immediately see what kind of differences that each term is approximated with. The notation \( \overline{q}^{x} \) also specifies that the variable coefficient is approximated by an arithmetic mean, the definition being \( [\overline{q}^{x}]_{i+\half}=(q_i+q_{i+1})/2 \).
Before implementing, it remains to solve (208) with respect to \( u_i^{n+1} \): $$ \begin{align} u^{n+1}_i &= - u_i^{n-1} + 2u_i^n + \nonumber\\ &\quad \left(\frac{\Delta t}{\Delta x}\right)^2 \left( \half(q_{i} + q_{i+1})(u_{i+1}^n - u_{i}^n) - \half(q_{i} + q_{i-1})(u_{i}^n - u_{i-1}^n)\right) + \nonumber\\ & \quad \Delta t^2 f^n_i \tp \tag{209} \end{align} $$
The stability criterion derived in the section Stability reads \( \Delta t\leq \Delta x/c \). If \( c=c(x) \), the criterion will depend on the spatial location. We must therefore choose a \( \Delta t \) that is small enough such that no mesh cell has \( \Delta x/c(x) >\Delta t \). That is, we must use the largest \( c \) value in the criterion: $$ \begin{equation} \Delta t \leq \beta \frac{\Delta x}{\max_{x\in [0,L]}c(x)} \tp \tag{210} \end{equation} $$ The parameter \( \beta \) is included as a safety factor: in some problems with a significantly varying \( c \) it turns out that one must choose \( \beta < 1 \) to have stable solutions (\( \beta =0.9 \) may act as an all-round value).
A different strategy to handle the stability criterion with variable wave velocity is to use a spatially varying \( \Delta t \). While the idea is mathematically attractive at first sight, the implementation quickly becomes very complicated, so we stick to a constant \( \Delta t \) and a worst case value of \( c(x) \) (with a safety factor \( \beta \)).
Consider a Neumann condition \( \partial u/\partial x=0 \) at \( x=L=N_x\Delta x \), discretized as $$ [D_{2x} u]^n_i = \frac{u_{i+1}^{n} - u_{i-1}^n}{2\Delta x} = 0\quad\Rightarrow\quad u_{i+1}^n = u_{i-1}^n, $$ for \( i=N_x \). Using the scheme (209) at the end point \( i=N_x \) with \( u_{i+1}^n=u_{i-1}^n \) results in $$ \begin{align} u^{n+1}_i &= - u_i^{n-1} + 2u_i^n + \nonumber\\ &\quad \left(\frac{\Delta t}{\Delta x}\right)^2 \left( q_{i+\half}(u_{i-1}^n - u_{i}^n) - q_{i-\half}(u_{i}^n - u_{i-1}^n)\right) + \Delta t^2 f^n_i \tag{211}\\ &= - u_i^{n-1} + 2u_i^n + \left(\frac{\Delta t}{\Delta x}\right)^2 (q_{i+\half} + q_{i-\half})(u_{i-1}^n - u_{i}^n) + \Delta t^2 f^n_i \tag{212}\\ &\approx - u_i^{n-1} + 2u_i^n + \left(\frac{\Delta t}{\Delta x}\right)^2 2q_{i}(u_{i-1}^n - u_{i}^n) + \Delta t^2 f^n_i \tp \tag{213} \end{align} $$ Here we used the approximation $$ \begin{align} q_{i+\half} + q_{i-\half} &= q_i + \left(\frac{dq}{dx}\right)_i \Delta x + \left(\frac{d^2q}{dx^2}\right)_i \Delta x^2 + \cdots +\nonumber\\ &\quad q_i - \left(\frac{dq}{dx}\right)_i \Delta x + \left(\frac{d^2q}{dx^2}\right)_i \Delta x^2 + \cdots\nonumber\\ &= 2q_i + 2\left(\frac{d^2q}{dx^2}\right)_i \Delta x^2 + {\cal O}(\Delta x^4) \nonumber\\ &\approx 2q_i \tp \tag{214} \end{align} $$
An alternative derivation may apply the arithmetic mean of \( q_{n-\half} \) and \( q_{n+\half} \) in (212), leading to the term $$ (q_i + \half(q_{i+1}+q_{i-1}))(u_{i-1}^n-u_i^n)\tp$$ Since \( \half(q_{i+1}+q_{i-1}) = q_i + {\cal O}(\Delta x^2) \), we can approximate with \( 2q_i(u_{i-1}^n-u_i^n) \) for \( i=N_x \) and get the same term as we did above.
A common technique when implementing \( \partial u/\partial x=0 \) boundary conditions, is to assume \( dq/dx=0 \) as well. This implies \( q_{i+1}=q_{i-1} \) and \( q_{i+1/2}=q_{i-1/2} \) for \( i=N_x \). The implications for the scheme are $$ \begin{align} u^{n+1}_i &= - u_i^{n-1} + 2u_i^n + \nonumber\\ &\quad \left(\frac{\Delta t}{\Delta x}\right)^2 \left( q_{i+\half}(u_{i-1}^n - u_{i}^n) - q_{i-\half}(u_{i}^n - u_{i-1}^n)\right) + \nonumber\\ & \quad \Delta t^2 f^n_i \tag{215}\\ &= - u_i^{n-1} + 2u_i^n + \left(\frac{\Delta t}{\Delta x}\right)^2 2q_{i-\half}(u_{i-1}^n - u_{i}^n) + \Delta t^2 f^n_i \tp \tag{216} \end{align} $$
The implementation of the scheme with a variable wave velocity \( q(x)=c^2(x) \)
may assume that \( q \) is available as an array q[i] at
the spatial mesh points. The following loop is a straightforward
implementation of the scheme (209):
for i in range(1, Nx):
u[i] = - u_nm1[i] + 2*u_n[i] + \
C2*(0.5*(q[i] + q[i+1])*(u_n[i+1] - u_n[i]) - \
0.5*(q[i] + q[i-1])*(u_n[i] - u_n[i-1])) + \
dt2*f(x[i], t[n])
C2 is now defined as (dt/dx)**2, i.e., not as the
squared Courant number, since the wave velocity is variable and appears
inside the parenthesis.
With Neumann conditions \( u_x=0 \) at the
boundary, we need to combine this scheme with the discrete
version of the boundary condition, as shown in the section Neumann condition and a variable coefficient.
Nevertheless, it would be convenient to reuse the formula for the
interior points and just modify the indices ip1=i+1 and im1=i-1
as we did in the section Implementation of Neumann conditions. Assuming
\( dq/dx=0 \) at the boundaries, we can implement the scheme at
the boundary with the following code.
i = 0
ip1 = i+1
im1 = ip1
u[i] = - u_nm1[i] + 2*u_n[i] + \
C2*(0.5*(q[i] + q[ip1])*(u_n[ip1] - u_n[i]) - \
0.5*(q[i] + q[im1])*(u_n[i] - u_n[im1])) + \
dt2*f(x[i], t[n])
With ghost cells we can just reuse the formula for the interior points also at the boundary, provided that the ghost values of both \( u \) and \( q \) are correctly updated to ensure \( u_x=0 \) and \( q_x=0 \).
A vectorized version of the scheme with a variable coefficient at internal mesh points becomes
u[1:-1] = - u_nm1[1:-1] + 2*u_n[1:-1] + \
C2*(0.5*(q[1:-1] + q[2:])*(u_n[2:] - u_n[1:-1]) -
0.5*(q[1:-1] + q[:-2])*(u_n[1:-1] - u_n[:-2])) + \
dt2*f(x[1:-1], t[n])
Sometimes a wave PDE has a variable coefficient in front of the time-derivative term: $$ \begin{equation} \varrho(x)\frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) + f(x,t) \tag{217} \tp \end{equation} $$ One example appears when modeling elastic waves in a rod with varying density, cf. (Waves on a string) with \( \varrho (x) \).
A natural scheme for (217) is $$ \begin{equation} [\varrho D_tD_t u = D_x\overline{q}^xD_x u + f]^n_i \tp \tag{218} \end{equation} $$ We realize that the \( \varrho \) coefficient poses no particular difficulty, since \( \varrho \) enters the formula just as a simple factor in front of a derivative. There is hence no need for any averaging of \( \varrho \). Often, \( \varrho \) will be moved to the right-hand side, also without any difficulty: $$ \begin{equation} [D_tD_t u = \varrho^{-1}D_x\overline{q}^xD_x u + f]^n_i \tp \tag{219} \end{equation} $$
Waves die out by two mechanisms. In 2D and 3D the energy of the wave spreads out in space, and energy conservation then requires the amplitude to decrease. This effect is not present in 1D. Damping is another cause of amplitude reduction. For example, the vibrations of a string die out because of damping due to air resistance and non-elastic effects in the string.
The simplest way of including damping is to add a first-order derivative to the equation (in the same way as friction forces enter a vibrating mechanical system): $$ \begin{equation} \frac{\partial^2 u}{\partial t^2} + b\frac{\partial u}{\partial t} = c^2\frac{\partial^2 u}{\partial x^2} + f(x,t), \tag{220} \end{equation} $$ where \( b \geq 0 \) is a prescribed damping coefficient.
A typical discretization of (220) in terms of centered differences reads $$ \begin{equation} [D_tD_t u + bD_{2t}u = c^2D_xD_x u + f]^n_i \tp \tag{221} \end{equation} $$ Writing out the equation and solving for the unknown \( u^{n+1}_i \) gives the scheme $$ \begin{equation} u^{n+1}_i = (1 + {\half}b\Delta t)^{-1}(({\half}b\Delta t -1) u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right) + \Delta t^2 f^n_i), \tag{222} \end{equation} $$ for \( i\in\seti{\Ix} \) and \( n\geq 1 \). New equations must be derived for \( u^1_i \), and for boundary points in case of Neumann conditions.
The damping is very small in many wave phenomena and thus only evident for very long time simulations. This makes the standard wave equation without damping relevant for a lot of applications.
The program wave1D_dn_vc.py is a fairly general code for 1D wave propagation problems that targets the following initial-boundary value problem $$ \begin{align} u_{tt} &= (c^2(x)u_x)_x + f(x,t),\quad &x\in (0,L),\ t\in (0,T] \tag{223}\\ u(x,0) &= I(x),\quad &x\in [0,L] \tag{224}\\ u_t(x,0) &= V(t),\quad &x\in [0,L] \tag{225}\\ u(0,t) &= U_0(t)\hbox{ or } u_x(0,t)=0,\quad &t\in (0,T] \tag{226}\\ u(L,t) &= U_L(t)\hbox{ or } u_x(L,t)=0,\quad &t\in (0,T] \tag{227} \end{align} $$
The only new feature here is the time-dependent Dirichlet conditions. These are trivial to implement:
i = Ix[0] # x=0
u[i] = U_0(t[n+1])
i = Ix[-1] # x=L
u[i] = U_L(t[n+1])
The solver function is a natural extension of the simplest
solver function in the initial wave1D_u0.py program,
extended with Neumann boundary conditions (\( u_x=0 \)),
time-varying Dirichlet conditions, as well as
a variable wave velocity. The different code segments needed
to make these extensions have been shown and commented upon in the
preceding text. We refer to the solver function in the
wave1D_dn_vc.py file for all the details. Note in that
solver function, however, that the technique of "hashing" is
used to check whether a certain simulation has been run before, or not.
This technique is further explained in the section Using a hash to create a file or directory name.
The vectorization is only applied inside the time loop, not for the initial condition or the first time steps, since this initial work is negligible for long time simulations in 1D problems.
The following sections explain various more advanced programming techniques applied in the general 1D wave equation solver.
A useful feature in the wave1D_dn_vc.py program is the specification
of the user_action function as a class. This part of the program may
need some motivation and explanation. Although the plot_u_st
function (and the PlotMatplotlib class) in the wave1D_u0.viz
function remembers the local variables in the viz function, it is a
cleaner solution to store the needed variables together with the
function, which is exactly what a class offers.
A class for flexible plotting, cleaning up files, making movie
files, like the function wave1D_u0.viz did, can be coded as follows:
class PlotAndStoreSolution:
"""
Class for the user_action function in solver.
Visualizes the solution only.
"""
def __init__(
self,
casename='tmp', # Prefix in filenames
umin=-1, umax=1, # Fixed range of y axis
pause_between_frames=None, # Movie speed
backend='matplotlib', # or 'gnuplot' or None
screen_movie=True, # Show movie on screen?
title='', # Extra message in title
skip_frame=1, # Skip every skip_frame frame
filename=None): # Name of file with solutions
self.casename = casename
self.yaxis = [umin, umax]
self.pause = pause_between_frames
self.backend = backend
if backend is None:
# Use native matplotlib
import matplotlib.pyplot as plt
elif backend in ('matplotlib', 'gnuplot'):
module = 'scitools.easyviz.' + backend + '_'
exec('import %s as plt' % module)
self.plt = plt
self.screen_movie = screen_movie
self.title = title
self.skip_frame = skip_frame
self.filename = filename
if filename is not None:
# Store time points when u is written to file
self.t = []
filenames = glob.glob('.' + self.filename + '*.dat.npz')
for filename in filenames:
os.remove(filename)
# Clean up old movie frames
for filename in glob.glob('frame_*.png'):
os.remove(filename)
def __call__(self, u, x, t, n):
"""
Callback function user_action, call by solver:
Store solution, plot on screen and save to file.
"""
# Save solution u to a file using numpy.savez
if self.filename is not None:
name = 'u%04d' % n # array name
kwargs = {name: u}
fname = '.' + self.filename + '_' + name + '.dat'
np.savez(fname, **kwargs)
self.t.append(t[n]) # store corresponding time value
if n == 0: # save x once
np.savez('.' + self.filename + '_x.dat', x=x)
# Animate
if n % self.skip_frame != 0:
return
title = 't=%.3f' % t[n]
if self.title:
title = self.title + ' ' + title
if self.backend is None:
# native matplotlib animation
if n == 0:
self.plt.ion()
self.lines = self.plt.plot(x, u, 'r-')
self.plt.axis([x[0], x[-1],
self.yaxis[0], self.yaxis[1]])
self.plt.xlabel('x')
self.plt.ylabel('u')
self.plt.title(title)
self.plt.legend(['t=%.3f' % t[n]])
else:
# Update new solution
self.lines[0].set_ydata(u)
self.plt.legend(['t=%.3f' % t[n]])
self.plt.draw()
else:
# scitools.easyviz animation
self.plt.plot(x, u, 'r-',
xlabel='x', ylabel='u',
axis=[x[0], x[-1],
self.yaxis[0], self.yaxis[1]],
title=title,
show=self.screen_movie)
# pause
if t[n] == 0:
time.sleep(2) # let initial condition stay 2 s
else:
if self.pause is None:
pause = 0.2 if u.size < 100 else 0
time.sleep(pause)
self.plt.savefig('frame_%04d.png' % (n))
Understanding this class requires quite some familiarity with Python
in general and class programming in particular.
The class supports plotting with Matplotlib (backend=None) or
SciTools (backend=matplotlib or backend=gnuplot) for maximum
flexibility.
The constructor shows how we can flexibly import the plotting engine
as (typically) scitools.easyviz.gnuplot_ or
scitools.easyviz.matplotlib_ (note the trailing underscore - it is required).
With the screen_movie parameter
we can suppress displaying each movie frame on the screen.
Alternatively, for slow movies associated with
fine meshes, one can set
skip_frame=10, causing every 10 frames to be shown.
The __call__ method makes PlotAndStoreSolution instances behave like
functions, so we can just pass an instance, say p, as the
user_action argument in the solver function, and any call to
user_action will be a call to p.__call__. The __call__
method plots the solution on the screen,
saves the plot to file, and stores the solution in a file for
later retrieval.
More details on storing the solution in files appear in the section Saving large arrays in files.
The function pulse in wave1D_dn_vc.py demonstrates wave motion in
heterogeneous media where \( c \) varies. One can specify an interval
where the wave velocity is decreased by a factor slowness_factor
(or increased by making this factor less than one).
Figure 28 shows a typical simulation
scenario.
Four types of initial conditions are available:
plug),gaussian),cosinehat),half-cosinehat)loc='center') or at the left end (loc='left') of the domain.
With the pulse in the middle, it splits in two parts, each with half
the initial amplitude, traveling in opposite directions. With the
pulse at the left end, centered at \( x=0 \), and using the symmetry
condition \( \partial u/\partial x=0 \), only a right-going pulse is
generated. There is also a left-going pulse, but it travels from \( x=0 \)
in negative \( x \) direction and is not visible in the domain \( [0,L] \).
The pulse function is a flexible tool for playing around with
various wave shapes and jumps in the wave velocity (i.e.,
discontinuous media). The code is shown to demonstrate how easy it is
to reach this flexibility with the building blocks we have already
developed:
def pulse(
C=1, # Maximum Courant number
Nx=200, # spatial resolution
animate=True,
version='vectorized',
T=2, # end time
loc='left', # location of initial condition
pulse_tp='gaussian', # pulse/init.cond. type
slowness_factor=2, # inverse of wave vel. in right medium
medium=[0.7, 0.9], # interval for right medium
skip_frame=1, # skip frames in animations
sigma=0.05 # width measure of the pulse
):
"""
Various peaked-shaped initial conditions on [0,1].
Wave velocity is decreased by the slowness_factor inside
medium. The loc parameter can be 'center' or 'left',
depending on where the initial pulse is to be located.
The sigma parameter governs the width of the pulse.
"""
# Use scaled parameters: L=1 for domain length, c_0=1
# for wave velocity outside the domain.
L = 1.0
c_0 = 1.0
if loc == 'center':
xc = L/2
elif loc == 'left':
xc = 0
if pulse_tp in ('gaussian','Gaussian'):
def I(x):
return np.exp(-0.5*((x-xc)/sigma)**2)
elif pulse_tp == 'plug':
def I(x):
return 0 if abs(x-xc) > sigma else 1
elif pulse_tp == 'cosinehat':
def I(x):
# One period of a cosine
w = 2
a = w*sigma
return 0.5*(1 + np.cos(np.pi*(x-xc)/a)) \
if xc - a <= x <= xc + a else 0
elif pulse_tp == 'half-cosinehat':
def I(x):
# Half a period of a cosine
w = 4
a = w*sigma
return np.cos(np.pi*(x-xc)/a) \
if xc - 0.5*a <= x <= xc + 0.5*a else 0
else:
raise ValueError('Wrong pulse_tp="%s"' % pulse_tp)
def c(x):
return c_0/slowness_factor \
if medium[0] <= x <= medium[1] else c_0
umin=-0.5; umax=1.5*I(xc)
casename = '%s_Nx%s_sf%s' % \
(pulse_tp, Nx, slowness_factor)
action = PlotMediumAndSolution(
medium, casename=casename, umin=umin, umax=umax,
skip_frame=skip_frame, screen_movie=animate,
backend=None, filename='tmpdata')
# Choose the stability limit with given Nx, worst case c
# (lower C will then use this dt, but smaller Nx)
dt = (L/Nx)/c_0
cpu, hashed_input = solver(
I=I, V=None, f=None, c=c,
U_0=None, U_L=None,
L=L, dt=dt, C=C, T=T,
user_action=action,
version=version,
stability_safety_factor=1)
if cpu > 0: # did we generate new data?
action.close_file(hashed_input)
action.make_movie_file()
print 'cpu (-1 means no new data generated):', cpu
def convergence_rates(
u_exact,
I, V, f, c, U_0, U_L, L,
dt0, num_meshes,
C, T, version='scalar',
stability_safety_factor=1.0):
"""
Half the time step and estimate convergence rates for
for num_meshes simulations.
"""
class ComputeError:
def __init__(self, norm_type):
self.error = 0
def __call__(self, u, x, t, n):
"""Store norm of the error in self.E."""
error = np.abs(u - u_exact(x, t[n])).max()
self.error = max(self.error, error)
E = []
h = [] # dt, solver adjusts dx such that C=dt*c/dx
dt = dt0
for i in range(num_meshes):
error_calculator = ComputeError('Linf')
solver(I, V, f, c, U_0, U_L, L, dt, C, T,
user_action=error_calculator,
version='scalar',
stability_safety_factor=1.0)
E.append(error_calculator.error)
h.append(dt)
dt /= 2 # halve the time step for next simulation
print 'E:', E
print 'h:', h
r = [np.log(E[i]/E[i-1])/np.log(h[i]/h[i-1])
for i in range(1,num_meshes)]
return r
def test_convrate_sincos():
n = m = 2
L = 1.0
u_exact = lambda x, t: np.cos(m*np.pi/L*t)*np.sin(m*np.pi/L*x)
r = convergence_rates(
u_exact=u_exact,
I=lambda x: u_exact(x, 0),
V=lambda x: 0,
f=0,
c=1,
U_0=0,
U_L=0,
L=L,
dt0=0.1,
num_meshes=6,
C=0.9,
T=1,
version='scalar',
stability_safety_factor=1.0)
print 'rates sin(x)*cos(t) solution:', \
[round(r_,2) for r_ in r]
assert abs(r[-1] - 2) < 0.002
PlotMediumAndSolution class used here is a subclass of
PlotAndStoreSolution where the medium with reduced \( c \) value,
as specified by the medium interval,
is visualized in the plots.
The argument \( N_x \) in the pulse function does not correspond to
the actual spatial resolution of \( C < 1 \), since the solver
function takes a fixed \( \Delta t \) and \( C \), and adjusts \( \Delta x \)
accordingly. As seen in the pulse function,
the specified \( \Delta t \) is chosen according to the
limit \( C=1 \), so if \( C < 1 \), \( \Delta t \) remains the same, but the
solver function operates with a larger \( \Delta x \) and smaller
\( N_x \) than was specified in the call to pulse. The practical reason
is that we always want to keep \( \Delta t \) fixed such that
plot frames and movies are synchronized in time regardless of the
value of \( C \) (i.e., \( \Delta x \) is varied when the
Courant number varies).
The reader is encouraged to play around with the pulse function:
>>> import wave1D_dn_vc as w
>>> w.pulse(Nx=50, loc='left', pulse_tp='cosinehat', slowness_factor=2)
Terminal> python -c 'import wave1D_dn_vc as w; w.pulse(...)'
Consider the wave equation with damping (220). The goal is to find an exact solution to a wave problem with damping and zero source term. A starting point is the standing wave solution from Exercise 2.1: Simulate a standing wave. It becomes necessary to include a damping term \( e^{-\beta t} \) and also have both a sine and cosine component in time: $$ \uex(x,t) = e^{-\beta t} \sin kx \left( A\cos\omega t + B\sin\omega t\right) \tp $$ Find \( k \) from the boundary conditions \( u(0,t)=u(L,t)=0 \). Then use the PDE to find constraints on \( \beta \), \( \omega \), \( A \), and \( B \). Set up a complete initial-boundary value problem and its solution.
Filename: damped_waves.
Consider the simple "plug" wave where \( \Omega = [-L,L] \) and $$ \begin{equation*} I(x) = \left\lbrace\begin{array}{ll} 1, & x\in [-\delta, \delta],\\ 0, & \hbox{otherwise} \end{array}\right. \end{equation*} $$ for some number \( 0 < \delta < L \). The other initial condition is \( u_t(x,0)=0 \) and there is no source term \( f \). The boundary conditions can be set to \( u=0 \). The solution to this problem is symmetric around \( x=0 \). This means that we can simulate the wave process in only the half of the domain \( [0,L] \).
a) Argue why the symmetry boundary condition is \( u_x=0 \) at \( x=0 \).
Hint. Symmetry of a function about \( x=x_0 \) means that \( f(x_0+h) = f(x_0-h) \).
b) Perform simulations of the complete wave problem on \( [-L,L] \). Thereafter, utilize the symmetry of the solution and run a simulation in half of the domain \( [0,L] \), using a boundary condition at \( x=0 \). Compare plots from the two solutions and confirm that they are the same.
c) Prove the symmetry property of the solution by setting up the complete initial-boundary value problem and showing that if \( u(x,t) \) is a solution, then also \( u(-x,t) \) is a solution.
d)
If the code works correctly, the solution \( u(x,t) = x(L-x)(1+\frac{t}{2}) \)
should be reproduced exactly. Write a test function test_quadratic that
checks whether this is the case. Simulate for \( x \) in \( [0, \frac{L}{2}] \) with
a symmetry condition at the end \( x = \frac{L}{2} \).
Filename: wave1D_symmetric.
Use the pulse function in wave1D_dn_vc.py to investigate
sending a pulse, located with its peak at \( x=0 \), through two
media with different wave velocities. The (scaled) velocity in
the left medium is 1 while it is \( \frac{1}{s_f} \) in the right medium.
Report what happens with a Gaussian pulse, a "cosine hat" pulse,
half a "cosine hat" pulse, and a plug pulse for resolutions
\( N_x=40,80,160 \), and \( s_f=2,4 \). Simulate until \( T=2 \).
Filename: pulse1D.
The experiments performed in Exercise 2.9: Send pulse waves through a layered medium shows
considerable numerical noise in the form of non-physical waves,
especially for \( s_f=4 \) and the plug pulse or the half a "cosinehat"
pulse. The noise is much less visible for a Gaussian pulse. Run the
case with the plug and half a "cosinehat" pulses for \( s_f=1 \), \( C=0.9,
0.25 \), and \( N_x=40,80,160 \). Use the numerical dispersion relation to
explain the observations.
Filename: pulse1D_analysis.
Harmonic means are often used if the wave velocity is non-smooth or
discontinuous. Will harmonic averaging of the wave velocity give less
numerical noise for the case \( s_f=4 \) in Exercise 2.9: Send pulse waves through a layered medium?
Filename: pulse1D_harmonic.
To enable a wave to leave the computational domain and travel undisturbed through the boundary \( x=L \), one can in a one-dimensional problem impose the following condition, called a radiation condition or open boundary condition: $$ \begin{equation} \frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} = 0\tp \tag{228} \end{equation} $$ The parameter \( c \) is the wave velocity.
Show that (228) accepts a solution \( u = g_R(x-ct) \) (right-going wave), but not \( u = g_L(x+ct) \) (left-going wave). This means that (228) will allow any right-going wave \( g_R(x-ct) \) to pass through the boundary undisturbed.
A corresponding open boundary condition for a left-going wave through \( x=0 \) is $$ \begin{equation} \frac{\partial u}{\partial t} - c\frac{\partial u}{\partial x} = 0\tp \tag{229} \end{equation} $$
a) A natural idea for discretizing the condition (228) at the spatial end point \( i=N_x \) is to apply centered differences in time and space: $$ \begin{equation} [D_{2t}u + cD_{2x}u =0]^n_{i},\quad i=N_x\tp \tag{230} \end{equation} $$ Eliminate the fictitious value \( u_{N_x+1}^n \) by using the discrete equation at the same point.
The equation for the first step, \( u_i^1 \), is in principle also affected, but we can then use the condition \( u_{N_x}=0 \) since the wave has not yet reached the right boundary.
b) A much more convenient implementation of the open boundary condition at \( x=L \) can be based on an explicit discretization $$ \begin{equation} [D^+_tu + cD_x^- u = 0]_i^n,\quad i=N_x\tp \tag{231} \end{equation} $$ From this equation, one can solve for \( u^{n+1}_{N_x} \) and apply the formula as a Dirichlet condition at the boundary point. However, the finite difference approximations involved are of first order.
Implement this scheme for a wave equation \( u_{tt}=c^2u_{xx} \) in a domain \( [0,L] \), where you have \( u_x=0 \) at \( x=0 \), the condition (228) at \( x=L \), and an initial disturbance in the middle of the domain, e.g., a plug profile like $$ u(x,0) = \left\lbrace\begin{array}{ll} 1,& L/2-\ell \leq x \leq L/2+\ell,\\ 0,\hbox{otherwise}\end{array}\right. $$ Observe that the initial wave is split in two, the left-going wave is reflected at \( x=0 \), and both waves travel out of \( x=L \), leaving the solution as \( u=0 \) in \( [0,L] \). Use a unit Courant number such that the numerical solution is exact. Make a movie to illustrate what happens.
Because this simplified implementation of the open boundary condition works, there is no need to pursue the more complicated discretization in a).
Hint. Modify the solver function in wave1D_dn.py.
c) Add the possibility to have either \( u_x=0 \) or an open boundary condition at the left boundary. The latter condition is discretized as $$ \begin{equation} [D^+_tu - cD_x^+ u = 0]_i^n,\quad i=0, \tag{232} \end{equation} $$ leading to an explicit update of the boundary value \( u^{n+1}_0 \).
The implementation can be tested with a Gaussian function as initial condition: $$ g(x;m,s) = \frac{1}{\sqrt{2\pi}s}e^{-\frac{(x-m)^2}{2s^2}}\tp$$ Run two tests:
d) In 2D and 3D it is difficult to compute the correct wave velocity normal to the boundary, which is needed in generalizations of the open boundary conditions in higher dimensions. Test the effect of having a slightly wrong wave velocity in (231). Make movies to illustrate what happens.
Filename: wave1D_open_BC.
The condition (228) works perfectly in 1D when \( c \) is known. In 2D and 3D, however, the condition reads \( u_t + c_x u_x + c_y u_y=0 \), where \( c_x \) and \( c_y \) are the wave speeds in the \( x \) and \( y \) directions. Estimating these components (i.e., the direction of the wave) is often challenging. Other methods are normally used in 2D and 3D to let waves move out of a computational domain.
It is frequently of interest to follow wave motion over large distances and long times. A straightforward approach is to work with a very large domain, but that might lead to a lot of computations in areas of the domain where the waves cannot be noticed. A more efficient approach is to let a right-going wave out of the domain and at the same time let it enter the domain on the left. This is called a periodic boundary condition.
The boundary condition at the right end \( x=L \) is an open boundary condition (see Problem 2.12: Implement open boundary conditions) to let a right-going wave out of the domain. At the left end, \( x=0 \), we apply, in the beginning of the simulation, either a symmetry boundary condition (see Problem 2.8: Explore symmetry boundary conditions) \( u_x=0 \), or an open boundary condition.
This initial wave will split in two and either be reflected or transported out of the domain at \( x=0 \). The purpose of the exercise is to follow the right-going wave. We can do that with a periodic boundary condition. This means that when the right-going wave hits the boundary \( x=L \), the open boundary condition lets the wave out of the domain, but at the same time we use a boundary condition on the left end \( x=0 \) that feeds the outgoing wave into the domain again. This periodic condition is simply \( u(0)=u(L) \). The switch from \( u_x=0 \) or an open boundary condition at the left end to a periodic condition can happen when \( u(L,t)>\epsilon \), where \( \epsilon =10^{-4} \) might be an appropriate value for determining when the right-going wave hits the boundary \( x=L \).
The open boundary conditions can conveniently be discretized as
explained in Problem 2.12: Implement open boundary conditions. Implement the
described type of boundary conditions and test them on two different
initial shapes: a plug \( u(x,0)=1 \) for \( x\leq 0.1 \), \( u(x,0)=0 \) for
\( x>0.1 \), and a Gaussian function in the middle of the domain:
\( u(x,0)=\exp{(-\frac{1}{2}(x-0.5)^2/0.05)} \). The domain is the unit
interval \( [0,1] \). Run these two shapes for Courant numbers 1 and
0.5. Assume constant wave velocity. Make movies of the four cases.
Reason why the solutions are correct.
Filename: periodic.
We have a 1D wave equation with variable wave velocity: \( u_{tt}=(qu_x)_x \). A Neumann condition \( u_x \) at \( x=0, L \) can be discretized as shown in (213) and (216).
The aim of this exercise is to examine the rate of the numerical error when using different ways of discretizing the Neumann condition.
a) As a test problem, \( q=1+(x-L/2)^4 \) can be used, with \( f(x,t) \) adapted such that the solution has a simple form, say \( u(x,t)=\cos (\pi x/L)\cos (\omega t) \) for, e.g., \( \omega = 1 \). Perform numerical experiments and find the convergence rate of the error using the approximation (213).
b) Switch to \( q(x)=1+\cos(\pi x/L) \), which is symmetric at \( x=0,L \), and check the convergence rate of the scheme (216). Now, \( q_{i-1/2} \) is a 2nd-order approximation to \( q_i \), \( q_{i-1/2}=q_i + 0.25q_i''\Delta x^2 + \cdots \), because \( q_i'=0 \) for \( i=N_x \) (a similar argument can be applied to the case \( i=0 \)).
c) A third discretization can be based on a simple and convenient, but less accurate, one-sided difference: \( u_{i}-u_{i-1}=0 \) at \( i=N_x \) and \( u_{i+1}-u_i=0 \) at \( i=0 \). Derive the resulting scheme in detail and implement it. Run experiments with \( q \) from a) or b) to establish the rate of convergence of the scheme.
d) A fourth technique is to view the scheme as $$ [D_tD_tu]^n_i = \frac{1}{\Delta x}\left( [qD_xu]_{i+\half}^n - [qD_xu]_{i-\half}^n\right) + [f]_i^n,$$ and place the boundary at \( x_{i+\half} \), \( i=N_x \), instead of exactly at the physical boundary. With this idea of approximating (moving) the boundary, we can just set \( [qD_xu]_{i+\half}^n=0 \). Derive the complete scheme using this technique. The implementation of the boundary condition at \( L-\Delta x/2 \) is \( \Oof{\Delta x^2} \) accurate, but the interesting question is what impact the movement of the boundary has on the convergence rate. Compute the errors as usual over the entire mesh and use \( q \) from a) or b).
Filename: Neumann_discr.
The purpose of this exercise is to verify the implementation of the
solver function in the program wave1D_n0.py by using an exact numerical solution
for the wave equation \( u_{tt}=c^2u_{xx} + f \) with Neumann boundary
conditions \( u_x(0,t)=u_x(L,t)=0 \).
A similar verification is used in the file wave1D_u0.py, which solves the same PDE, but with
Dirichlet boundary conditions \( u(0,t)=u(L,t)=0 \). The idea of the
verification test in function test_quadratic in wave1D_u0.py is to
produce a solution that is a lower-order polynomial such that both the
PDE problem, the boundary conditions, and all the discrete equations
are exactly fulfilled. Then the solver function should reproduce
this exact solution to machine precision. More precisely, we seek
\( u=X(x)T(t) \), with \( T(t) \) as a linear function and \( X(x) \) as a
parabola that fulfills the boundary conditions. Inserting this \( u \) in
the PDE determines \( f \). It turns out that \( u \) also fulfills the
discrete equations, because the truncation error of the discretized
PDE has derivatives in \( x \) and \( t \) of order four and higher. These
derivatives all vanish for a quadratic \( X(x) \) and linear \( T(t) \).
It would be attractive to use a similar approach in the case of Neumann conditions. We set \( u=X(x)T(t) \) and seek lower-order polynomials \( X \) and \( T \). To force \( u_x \) to vanish at the boundary, we let \( X_x \) be a parabola. Then \( X \) is a cubic polynomial. The fourth-order derivative of a cubic polynomial vanishes, so \( u=X(x)T(t) \) will fulfill the discretized PDE also in this case, if \( f \) is adjusted such that \( u \) fulfills the PDE.
However, the discrete boundary condition is not exactly fulfilled by this choice of \( u \). The reason is that $$ \begin{equation} [D_{2x}u]^n_i = u_{x}(x_i,t_n) + \frac{1}{6}u_{xxx}(x_i,t_n)\Delta x^2 + \Oof{\Delta x^4}\tp \tag{233} \end{equation} $$ At the boundary two boundary points, we must demand that the derivative \( X_x(x)=0 \) such that \( u_x=0 \). However, \( u_{xxx} \) is a constant and not zero when \( X(x) \) is a cubic polynomial. Therefore, our \( u=X(x)T(t) \) fulfills $$ [D_{2x}u]^n_i = \frac{1}{6}u_{xxx}(x_i,t_n)\Delta x^2, $$ and not $$ [D_{2x}u]^n_i =0, \quad i=0,N_x,$$ as it should. (Note that all the higher-order terms \( \Oof{\Delta x^4} \) also have higher-order derivatives that vanish for a cubic polynomial.) So to summarize, the fundamental problem is that \( u \) as a product of a cubic polynomial and a linear or quadratic polynomial in time is not an exact solution of the discrete boundary conditions.
To make progress,
we assume that \( u=X(x)T(t) \), where \( T \) for simplicity is taken as a
prescribed linear function \( 1+\frac{1}{2}t \), and \( X(x) \) is taken
as an unknown cubic polynomial \( \sum_{j=0}^3 a_jx^j \).
There are two different ways of determining the coefficients
\( a_0,\ldots,a_3 \) such that both the discretized PDE and the
discretized boundary conditions are fulfilled, under the
constraint that we can specify a function \( f(x,t) \) for the PDE to feed
to the solver function in wave1D_n0.py. Both approaches
are explained in the subexercises.
a) One can insert \( u \) in the discretized PDE and find the corresponding \( f \). Then one can insert \( u \) in the discretized boundary conditions. This yields two equations for the four coefficients \( a_0,\ldots,a_3 \). To find the coefficients, one can set \( a_0=0 \) and \( a_1=1 \) for simplicity and then determine \( a_2 \) and \( a_3 \). This approach will make \( a_2 \) and \( a_3 \) depend on \( \Delta x \) and \( f \) will depend on both \( \Delta x \) and \( \Delta t \).
Use sympy to perform analytical computations.
A starting point is to define \( u \) as follows:
def test_cubic1():
import sympy as sm
x, t, c, L, dx, dt = sm.symbols('x t c L dx dt')
i, n = sm.symbols('i n', integer=True)
# Assume discrete solution is a polynomial of degree 3 in x
T = lambda t: 1 + sm.Rational(1,2)*t # Temporal term
a = sm.symbols('a_0 a_1 a_2 a_3')
X = lambda x: sum(a[q]*x**q for q in range(4)) # Spatial term
u = lambda x, t: X(x)*T(t)
u(x,t)
with x and t as sympy symbols.
Define DxDx(u, i, n), DtDt(u, i, n), and D2x(u, i, n)
as Python functions for returning the difference
approximations \( [D_xD_x u]^n_i \), \( [D_tD_t u]^n_i \), and
\( [D_{2x}u]^n_i \). The next step is to set up the residuals
for the equations \( [D_{2x}u]^n_0=0 \) and \( [D_{2x}u]^n_{N_x}=0 \),
where \( N_x=L/\Delta x \). Call the residuals R_0 and R_L.
Substitute \( a_0 \) and \( a_1 \) by 0 and 1, respectively, in
R_0, R_L, and a:
R_0 = R_0.subs(a[0], 0).subs(a[1], 1)
R_L = R_L.subs(a[0], 0).subs(a[1], 1)
a = list(a) # enable in-place assignment
a[0:2] = 0, 1
a[2:]:
s = sm.solve([R_0, R_L], a[2:])
# s is dictionary with the unknowns a[2] and a[3] as keys
a[2:] = s[a[2]], s[a[3]]
a contains computed values and u will automatically use
these new values since X accesses a.
Compute the source term \( f \) from the discretized PDE:
\( f^n_i = [D_tD_t u - c^2D_xD_x u]^n_i \). Turn \( u \), the time
derivative \( u_t \) (needed for the initial condition \( V(x) \)),
and \( f \) into Python functions. Set numerical values for
\( L \), \( N_x \), \( C \), and \( c \). Prescribe the time interval as
\( \Delta t = CL/(N_xc) \), which imply \( \Delta x = c\Delta t/C = L/N_x \).
Define new functions I(x), V(x), and f(x,t) as wrappers of the ones
made above, where fixed values of \( L \), \( c \), \( \Delta x \), and \( \Delta t \)
are inserted, such that I, V, and f can be passed on to the
solver function. Finally, call solver with a user_action
function that compares the numerical solution to this exact
solution \( u \) of the discrete PDE problem.
Hint.
To turn a sympy expression e, depending on a series of
symbols, say x, t, dx, dt, L, and c, into a plain
Python function e_exact(x,t,L,dx,dt,c), one can write
e_exact = sm.lambdify([x,t,L,dx,dt,c], e, 'numpy')
'numpy' argument is a good habit as the e_exact function
will then work with array arguments if it contains mathematical
functions (but here we only do plain arithmetics, which automatically
work with arrays).
b)
An alternative way of determining \( a_0,\ldots,a_3 \) is to reason as
follows. We first construct \( X(x) \) such that the boundary conditions
are fulfilled: \( X=x(L-x) \). However, to compensate for the fact
that this choice of \( X \) does not fulfill the discrete boundary
condition, we seek \( u \) such that
$$ u_x = \frac{\partial}{\partial x}x(L-x)T(t) - \frac{1}{6}u_{xxx}\Delta x^2,$$
since this \( u \) will fit the discrete boundary condition.
Assuming \( u=T(t)\sum_{j=0}^3a_jx^j \), we can use the above equation to
determine the coefficients \( a_1,a_2,a_3 \). A value, e.g., 1 can be used for
\( a_0 \). The following sympy code computes this \( u \):
def test_cubic2():
import sympy as sm
x, t, c, L, dx = sm.symbols('x t c L dx')
T = lambda t: 1 + sm.Rational(1,2)*t # Temporal term
# Set u as a 3rd-degree polynomial in space
X = lambda x: sum(a[i]*x**i for i in range(4))
a = sm.symbols('a_0 a_1 a_2 a_3')
u = lambda x, t: X(x)*T(t)
# Force discrete boundary condition to be zero by adding
# a correction term the analytical suggestion x*(L-x)*T
# u_x = x*(L-x)*T(t) - 1/6*u_xxx*dx**2
R = sm.diff(u(x,t), x) - (
x*(L-x) - sm.Rational(1,6)*sm.diff(u(x,t), x, x, x)*dx**2)
# R is a polynomial: force all coefficients to vanish.
# Turn R to Poly to extract coefficients:
R = sm.poly(R, x)
coeff = R.all_coeffs()
s = sm.solve(coeff, a[1:]) # a[0] is not present in R
# s is dictionary with a[i] as keys
# Fix a[0] as 1
s[a[0]] = 1
X = lambda x: sm.simplify(sum(s[a[i]]*x**i for i in range(4)))
u = lambda x, t: X(x)*T(t)
print 'u:', u(x,t)
The next step is to find the source term f_e by inserting u_e
in the PDE. Thereafter, turn u, f, and the time derivative of u
into plain Python functions as in a), and then wrap these functions
in new functions I, V, and f, with the right signature as
required by the solver function. Set parameters as in a) and
check that the solution is exact to machine precision at each
time level using an appropriate user_action function.
Filename: wave1D_n0_test_cubic.