Analysis of finite difference equations

Model:

 
$$ \begin{equation} u'(t) = -au(t),\quad u(0)=I \tag{1} \end{equation} $$

Method:

 
$$ \begin{equation} u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n \tag{2} \end{equation} $$

Encouraging numerical solutions

\( I=1 \), \( a=2 \), \( \theta =1,0.5, 0 \), \( \Delta t=1.25, 0.75, 0.5, 0.1 \).

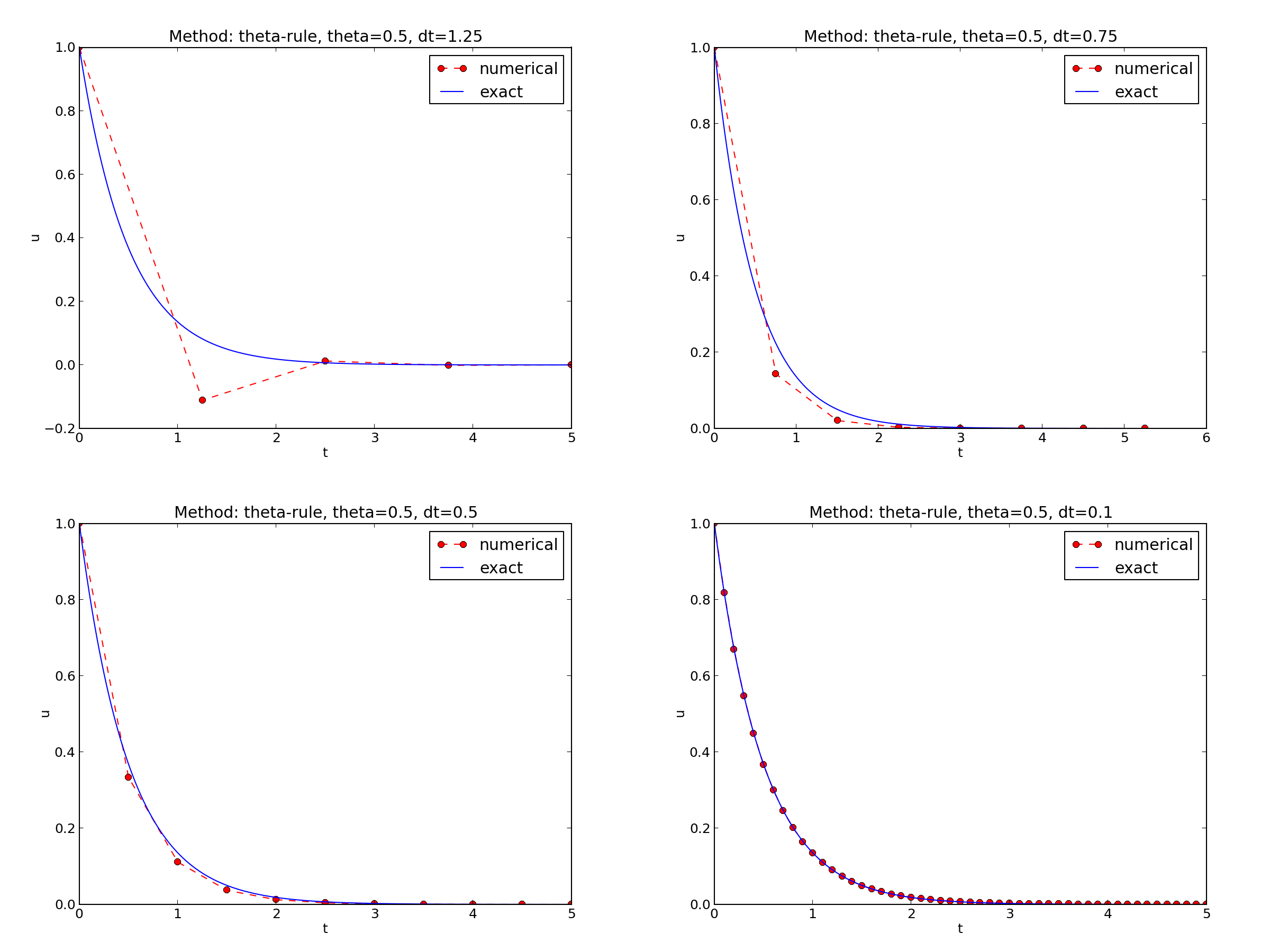
Discouraging numerical solutions; Crank-Nicolson

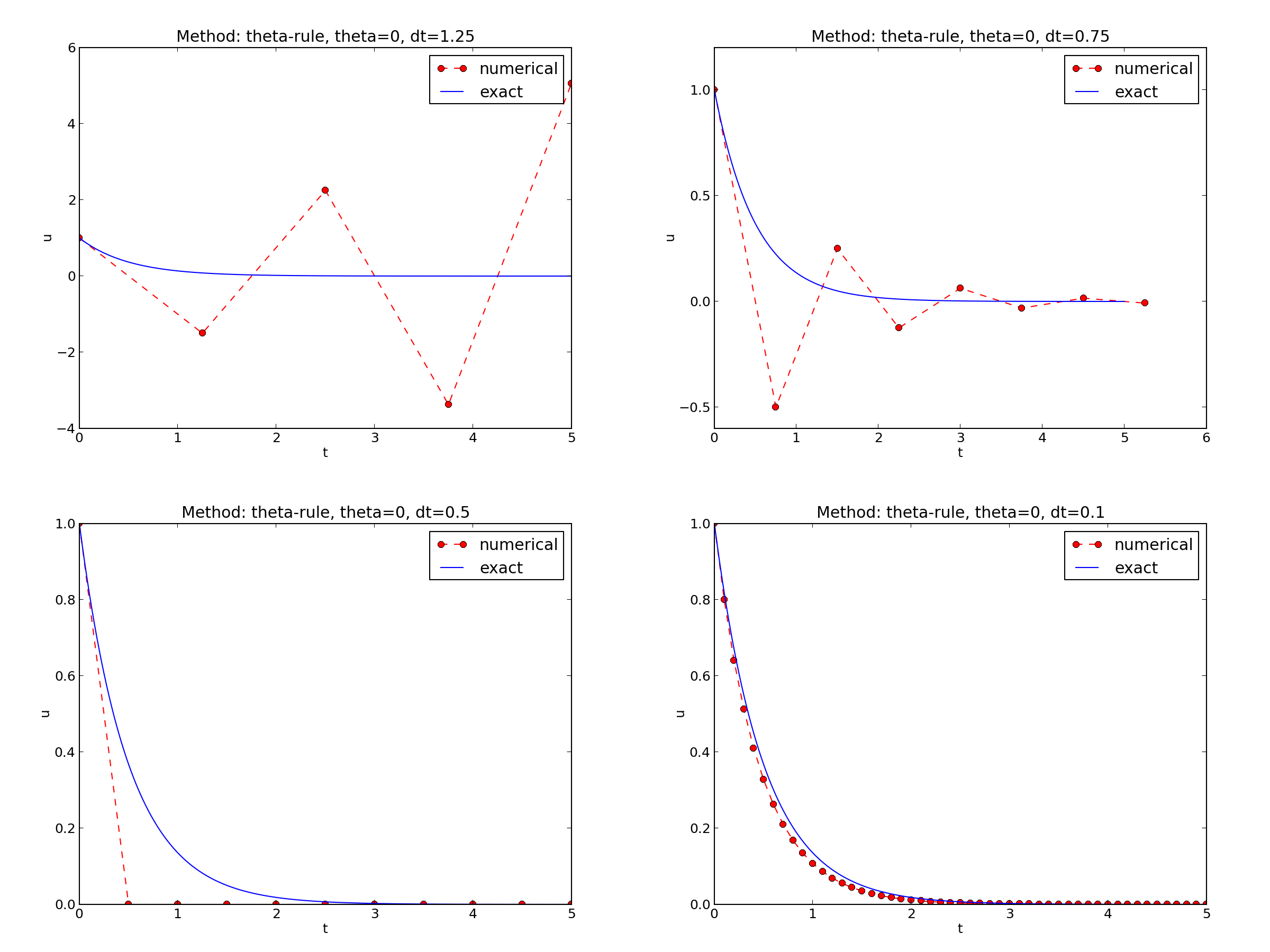
Discouraging numerical solutions; Forward Euler

Summary of observations

The characteristics of the displayed curves can be summarized as follows:

• The Backward Euler scheme always gives a monotone solution, lying above the exact solution.
• The Crank-Nicolson scheme gives the most accurate results, but for \( \Delta t=1.25 \) the solution oscillates.
• The Forward Euler scheme gives a growing, oscillating solution for \( \Delta t=1.25 \); a decaying, oscillating solution for \( \Delta t=0.75 \); a strange solution \( u^n=0 \) for \( n\geq 1 \) when \( \Delta t=0.5 \); and a solution seemingly as accurate as the one by the Backward Euler scheme for \( \Delta t = 0.1 \), but the curve lies below the exact solution.

Problem setting

Experimental investigation of oscillatory solutions

The solution is oscillatory if

 
$$ u^{n} > u^{n-1}$$

 
("Safe choices" of \( \Delta t \) lie under the following curve as a function of \( a \).)

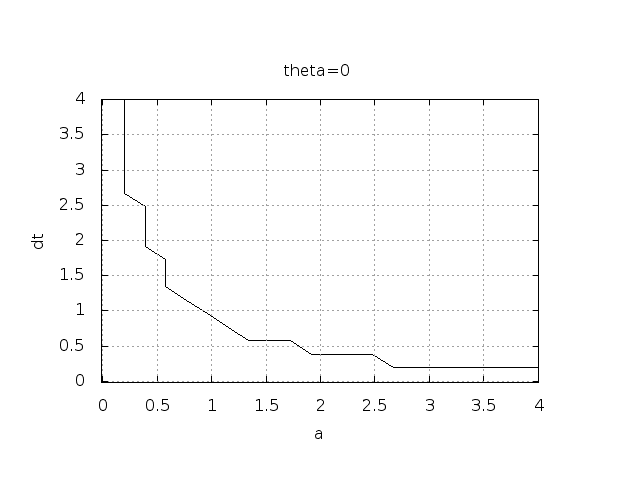
Seems that \( a\Delta t < 1 \) for FE and 2 for CN.

Exact numerical solution

Starting with \( u^0=I \), the simple recursion (2) can be applied repeatedly \( n \) times, with the result that

 
$$ \begin{equation} u^{n} = IA^n,\quad A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} \tag{3} \end{equation} $$

Such a formula for the exact discrete solution is unusual to obtain in practice, but very handy for our analysis here.

Note: An exact dicrete solution fulfills a discrete equation (without round-off errors), whereas an exact solution fulfills the original mathematical equation.

Stability

Since \( u^n=I A^n \),

• \( A < 0 \) gives a factor \( (-1)^n \) and oscillatory solutions
• \( |A|>1 \) gives growing solutions
• Recall: the exact solution is monotone and decaying
• If these qualitative properties are not met, we say that the numerical solution is unstable

Computation of stability in this problem

\( A < 0 \) if

 
$$ \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} < 0 $$

 
To avoid oscillatory solutions we must have \( A> 0 \) and

 
$$ \begin{equation} \Delta t < \frac{1}{(1-\theta)a}\ \tag{4} \end{equation} $$

• Always fulfilled for Backward Euler
• \( \Delta t \leq 1/a \) for Forward Euler
• \( \Delta t \leq 2/a \) for Crank-Nicolson

Computation of stability in this problem

\( |A|\leq 1 \) means \( -1\leq A\leq 1 \)

 
$$ \begin{equation} -1\leq\frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} \leq 1 \tag{5} \end{equation} $$

 
\( -1 \) is the critical limit (because \( A\le 1 \) is always satisfied):

 
$$ \begin{align*} \Delta t &\leq \frac{2}{(1-2\theta)a},\quad \mbox{when }\theta < \half \end{align*} $$

• Always fulfilled for Backward Euler and Crank-Nicolson
• \( \Delta t \leq 2/a \) for Forward Euler

Explanation of problems with Forward Euler

• \( a\Delta t= 2\cdot 1.25=2.5 \) and \( A=-1.5 \): oscillations and growth
• \( a\Delta t = 2\cdot 0.75=1.5 \) and \( A=-0.5 \): oscillations and decay
• \( \Delta t=0.5 \) and \( A=0 \): \( u^n=0 \) for \( n>0 \)
• Smaller \( \Delta t \): qualitatively correct solution

Explanation of problems with Crank-Nicolson

• \( \Delta t=1.25 \) and \( A=-0.25 \): oscillatory solution
• Never any growing solution

Summary of stability

1. Forward Euler is conditionally stable

• \( \Delta t < 2/a \) for avoiding growth
• \( \Delta t\leq 1/a \) for avoiding oscillations
2. The Crank-Nicolson is unconditionally stable wrt growth and conditionally stable wrt oscillations

• \( \Delta t < 2/a \) for avoiding oscillations
3. Backward Euler is unconditionally stable

Comparing amplification factors

\( u^{n+1} \) is an amplification \( A \) of \( u^n \):

 
$$ u^{n+1} = Au^n,\quad A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} $$

The exact solution is also an amplification:

 
$$ u(t_{n+1}) = \Aex u(t_n), \quad \Aex = e^{-a\Delta t}$$

A possible measure of accuracy: \( \Aex - A \)

Plot of amplification factors

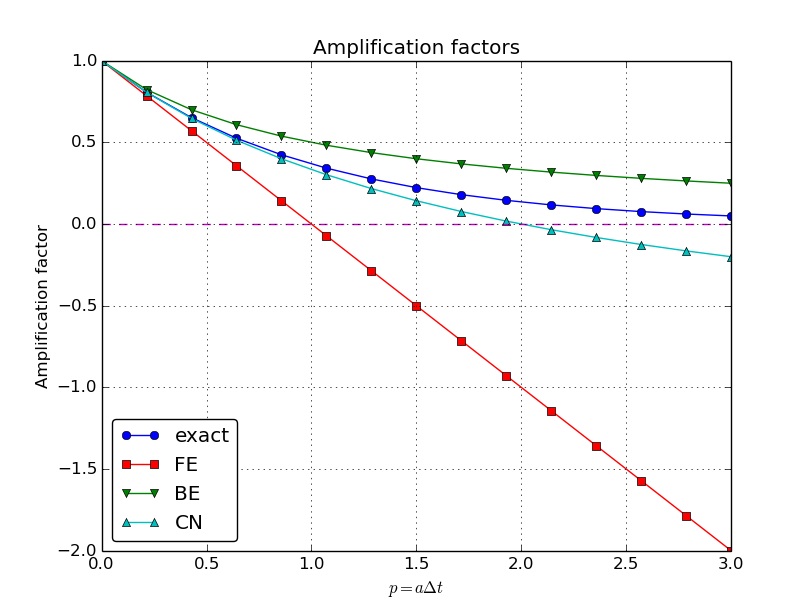
\( p=a\Delta t \) is the important parameter for numerical performance

• \( p=a\Delta t \) is a dimensionless parameter
• all expressions for stability and accuracy involve \( p \)
• Note that \( \Delta t \) alone is not so important, it is the combination with \( a \) through \( p=a\Delta t \) that matters

Series expansion of amplification factors

To investigate \( \Aex - A \) mathematically, we can Taylor expand the expression, using \( p=a\Delta t \) as variable.

>>> from sympy import *
>>> # Create p as a mathematical symbol with name 'p'
>>> p = Symbol('p')
>>> # Create a mathematical expression with p
>>> A_e = exp(-p)
>>>
>>> # Find the first 6 terms of the Taylor series of A_e
>>> A_e.series(p, 0, 6)
1 + (1/2)*p**2 - p - 1/6*p**3 - 1/120*p**5 + (1/24)*p**4 + O(p**6)

>>> theta = Symbol('theta')
>>> A = (1-(1-theta)*p)/(1+theta*p)
>>> FE = A_e.series(p, 0, 4) - A.subs(theta, 0).series(p, 0, 4)
>>> BE = A_e.series(p, 0, 4) - A.subs(theta, 1).series(p, 0, 4)
>>> half = Rational(1,2)  # exact fraction 1/2
>>> CN = A_e.series(p, 0, 4) - A.subs(theta, half).series(p, 0, 4)
>>> FE
(1/2)*p**2 - 1/6*p**3 + O(p**4)
>>> BE
-1/2*p**2 + (5/6)*p**3 + O(p**4)
>>> CN
(1/12)*p**3 + O(p**4)

Error in amplification factors

Focus: the error measure \( A-\Aex \) as function of \( \Delta t \) (recall that \( p=a\Delta t \)):

 
$$ \begin{equation} A-\Aex = \left\lbrace\begin{array}{ll} \Oof{\Delta t^2}, & \hbox{Forward and Backward Euler},\\ \Oof{\Delta t^3}, & \hbox{Crank-Nicolson} \end{array}\right. \tag{6} \end{equation} $$

The fraction of numerical and exact amplification factors

Focus: the error measure \( 1-A/\Aex \) as function of \( p=a\Delta t \):

>>> FE = 1 - (A.subs(theta, 0)/A_e).series(p, 0, 4)
>>> BE = 1 - (A.subs(theta, 1)/A_e).series(p, 0, 4)
>>> CN = 1 - (A.subs(theta, half)/A_e).series(p, 0, 4)
>>> FE
(1/2)*p**2 + (1/3)*p**3 + O(p**4)
>>> BE
-1/2*p**2 + (1/3)*p**3 + O(p**4)
>>> CN
(1/12)*p**3 + O(p**4)

Same leading-order terms as for the error measure \( A-\Aex \).

The true/global error at a point

• The error in \( A \) reflects the local (amplification) error when going from one time step to the next
• What is the global (true) error at \( t_n \)? \( e^n = \uex(t_n) - u^n = Ie^{-at_n} - IA^n \)
• Taylor series expansions of \( e^n \) simplify the expression

Computing the global error at a point

>>> n = Symbol('n')
>>> u_e = exp(-p*n)   # I=1
>>> u_n = A**n        # I=1
>>> FE = u_e.series(p, 0, 4) - u_n.subs(theta, 0).series(p, 0, 4)
>>> BE = u_e.series(p, 0, 4) - u_n.subs(theta, 1).series(p, 0, 4)
>>> CN = u_e.series(p, 0, 4) - u_n.subs(theta, half).series(p, 0, 4)
>>> FE
(1/2)*n*p**2 - 1/2*n**2*p**3 + (1/3)*n*p**3 + O(p**4)
>>> BE
(1/2)*n**2*p**3 - 1/2*n*p**2 + (1/3)*n*p**3 + O(p**4)
>>> CN
(1/12)*n*p**3 + O(p**4)

Substitute \( n \) by \( t/\Delta t \):

• Forward and Backward Euler: leading order term \( \half ta^2\Delta t \)
• Crank-Nicolson: leading order term \( \frac{1}{12}ta^3\Delta t^2 \)

Convergence

The numerical scheme is convergent if the global error \( e^n\rightarrow 0 \) as \( \Delta t\rightarrow 0 \). If the error has a leading order term \( \Delta t^r \), the convergence rate is of order \( r \).

Integrated errors

Focus: norm of the numerical error

 
$$ ||e^n||_{\ell^2} = \sqrt{\Delta t\sum_{n=0}^{N_t} ({\uex}(t_n) - u^n)^2}$$

Forward and Backward Euler:

 
$$ ||e^n||_{\ell^2} = \frac{1}{4}\sqrt{\frac{T^3}{3}} a^2\Delta t$$

Crank-Nicolson:

 
$$ ||e^n||_{\ell^2} = \frac{1}{12}\sqrt{\frac{T^3}{3}}a^3\Delta t^2$$

Truncation error

• How good is the discrete equation?
• Possible answer: see how well \( \uex \) fits the discrete equation

 
$$ \lbrack D^{+}_t u = -au\rbrack^n$$

 
i.e.,

 
$$ \frac{u^{n+1}-u^n}{\Delta t} = -au^n$$

 
Insert \( \uex \) (which does not in general fulfill this discrete equation):

 
$$ \begin{equation} \frac{\uex(t_{n+1})-\uex(t_n)}{\Delta t} + a\uex(t_n) = R^n \neq 0 \tag{7} \end{equation} $$

Computation of the truncation error

• The residual \( R^n \) is the truncation error.
• How does \( R^n \) vary with \( \Delta t \)?

Tool: Taylor expand \( \uex \) around the point where the ODE is sampled (here \( t_n \))

 
$$ \uex(t_{n+1}) = \uex(t_n) + \uex'(t_n)\Delta t + \half\uex''(t_n) \Delta t^2 + \cdots $$

 
Inserting this Taylor series in (7) gives

 
$$ R^n = \uex'(t_n) + \half\uex''(t_n)\Delta t + \ldots + a\uex(t_n)$$

 
Now, \( \uex \) solves the ODE \( \uex'=-a\uex \), and then

 
$$ R^n \approx \half\uex''(t_n)\Delta t$$

 
This is a mathematical expression for the truncation error.

The truncation error for other schemes

Backward Euler:

 
$$ R^n \approx -\half\uex''(t_n)\Delta t $$

Crank-Nicolson:

 
$$ R^{n+\half} \approx \frac{1}{24}\uex'''(t_{n+\half})\Delta t^2$$

Consistency, stability, and convergence

• Truncation error measures the residual in the difference equations. The scheme is consistent if the truncation error goes to 0 as \( \Delta t\rightarrow 0 \). Importance: the difference equations approaches the differential equation as \( \Delta t\rightarrow 0 \).
• Stability means that the numerical solution exhibits the same qualitative properties as the exact solution. Here: monotone, decaying function.
• Convergence implies that the true (global) error \( e^n =\uex(t_n)-u^n\rightarrow 0 \) as \( \Delta t\rightarrow 0 \). This is really what we want!

The Lax equivalence theorem for linear differential equations: consistency + stability is equivalent with convergence.

(Consistency and stability is in most problems much easier to establish than convergence.)