
This worked example
Contents
The following programming topics are illustrated
Scientific application
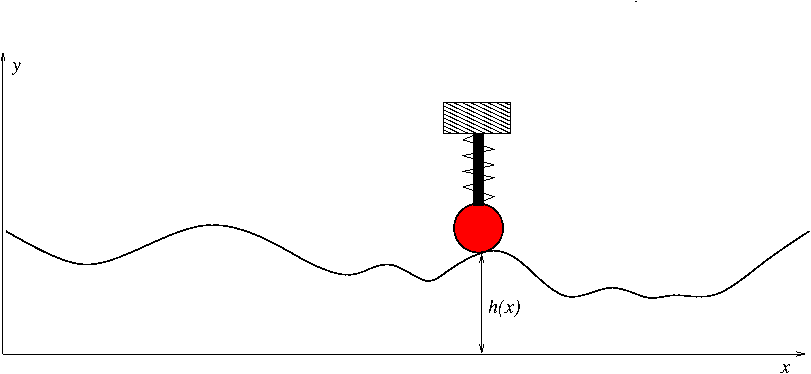
Physical problem and mathematical model
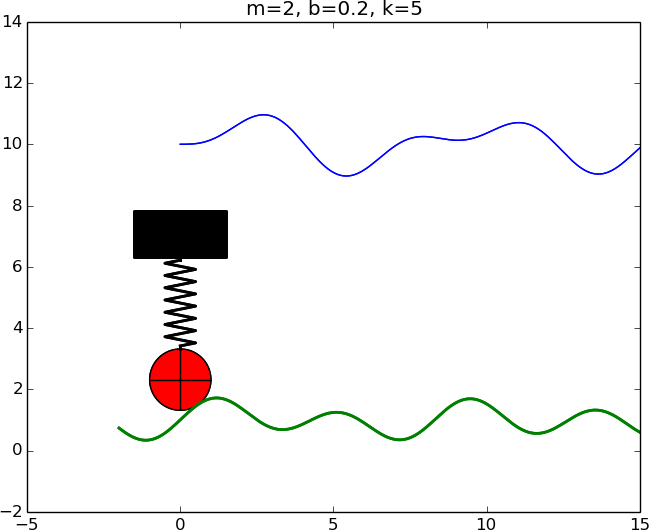
Relatively stiff spring \( k=5 \)
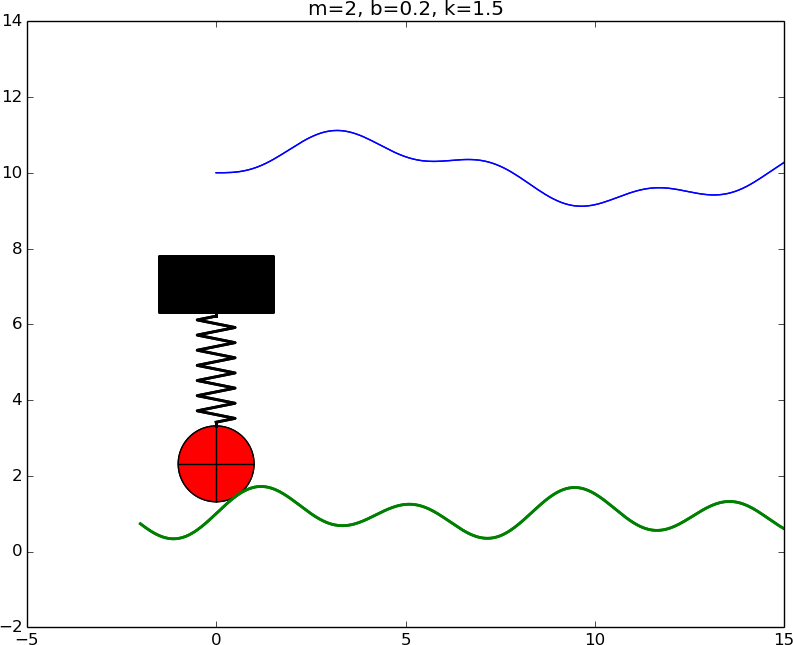
Softer spring \( k=1 \)
Numerical model
Extension to quadratic damping: \( f(u')=b|u'|u' \)
Simple implementation
Using the solver function to solve a problem
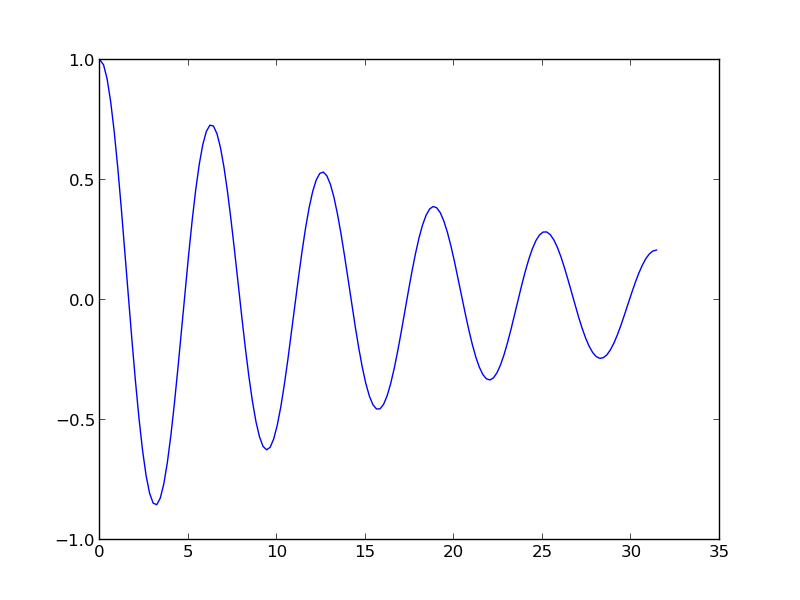
The resulting plot
More advanced implementation
The code (part I)
The code (part II)
Using the solver function to solve a problem
The resulting plot
Local vs global variables
Advanced programming of functions with parameters
The excitation force
The very basics of two-dimensional arrays
Computing the force from the road profile
Vectorized version of the previous function
Performing the simulation
A high-level solve function (part I)
A high-level solve function (part II)
Pickling: storing Python objects in files
Computing an expression for the noise level of the vibrations
User input
Positional command-line arguments
Option-value pairs on the command line
Example on using argparse
Running a simulation
Visual exploration
Code for loading data from file
Plotting the last part of \( u \)
Computing the derivative of \( u \)
Code for the derivative
How much faster is the vectorized version?
Computing the spectrum of signals
Plot of the spectra
Multiple plots in the same figure
Plot of the first realization
Advanced topics
Symbolic computing via SymPy
Go seamlessly from symbolic expression to Python function
Testing via test functions and test frameworks
Example on a test function
Test function for the numerical solver (part I)
Test function for the numerical solver (part II)
Test function for the numerical solver (part III)
Using a test framework
Modules
Example on a module file
What gets imported?

A special formula must be applied for \( n=0 \): $$ \begin{equation*} u^1 = u^0 + \Delta t\, V + \frac{\Delta t^2}{2m}(-bV - s(u^0) + F^0) \end{equation*} $$
Linearization via geometric mean: $$ f(u'(t_n)) = \left. |u'|u'\right\vert^n \approx |u'|^{n-\frac{1}{2}} (u')^{n+\frac{1}{2}} $$ $$ \begin{align*} u^{n+1} = & \left( m + b|u^n-u^{n-1}|\right)^{-1}\times \\ &\quad \left(2m u^n - mu^{n-1} + bu^n|u^n-u^{n-1}| + \Delta t^2 (F^n - s(u^n)) \right) \end{align*} $$
(and again a special formula for \( u^1 \))
from numpy import *
def solver_linear_damping(I, V, m, b, s, F, t):
N = t.size - 1 # No of time intervals
dt = t[1] - t[0] # Time step
u = zeros(N+1) # Result array
u[0] = I
u[1] = u[0] + dt*V + dt**2/(2*m)*(-b*V - s(u[0]) + F[0])
for n in range(1,N):
u[n+1] = 1./(m + b*dt/2)*(2*m*u[n] + \
(b*dt/2 - m)*u[n-1] + dt**2*(F[n] - s(u[n])))
return u
from solver import solver_linear_damping
from numpy import *
def s(u):
return 2*u
T = 10*pi # simulate for t in [0,T]
dt = 0.2
N = int(round(T/dt))
t = linspace(0, T, N+1)
F = zeros(t.size)
I = 1; V = 0
m = 2; b = 0.2
u = solver_linear_damping(I, V, m, b, s, F, t)
from matplotlib.pyplot import *
plot(t, u)
savefig('tmp.pdf') # save plot to PDF file
savefig('tmp.png') # save plot to PNG file
show()
Improvements:
>>> 2/3
0
>>> 2.0/3
0.6666666666666666
>>> 2/3.0
0.6666666666666666
At least one of the operands in division must be float
to get correct real division!
def solver(I, V, m, b, s, F, t, damping='linear'):
"""
Solve m*u'' + f(u') + s(u) = F for time points in t.
u(0)=I and u'(0)=V,
by a central finite difference method with time step dt.
If damping is 'linear', f(u')=b*u, while if damping is
'quadratic', we have f(u')=b*u'*abs(u').
s(u) is a Python function, while F may be a function
or an array (then F[i] corresponds to F at t[i]).
"""
N = t.size - 1 # No of time intervals
dt = t[1] - t[0] # Time step
u = np.zeros(N+1) # Result array
b = float(b); m = float(m) # Avoid integer division
# Convert F to array
if callable(F):
F = F(t)
elif isinstance(F, (list,tuple,np.ndarray)):
F = np.asarray(F)
else:
raise TypeError(
'F must be function or array, not %s' % type(F))
def solver(I, V, m, b, s, F, t, damping='linear'):
...
u[0] = I
if damping == 'linear':
u[1] = u[0] + dt*V + dt**2/(2*m)*(-b*V - s(u[0]) + F[0])
elif damping == 'quadratic':
u[1] = u[0] + dt*V + \
dt**2/(2*m)*(-b*V*abs(V) - s(u[0]) + F[0])
else:
raise ValueError('Wrong value: damping="%s"' % damping)
for n in range(1,N):
if damping == 'linear':
u[n+1] = (2*m*u[n] + (b*dt/2 - m)*u[n-1] +
dt**2*(F[n] - s(u[n])))/(m + b*dt/2)
elif damping == 'quadratic':
u[n+1] = (2*m*u[n] - m*u[n-1] + b*u[n]*abs(u[n] - u[n-1])
- dt**2*(s(u[n]) - F[n]))/\
(m + b*abs(u[n] - u[n-1]))
return u, t
import numpy as np
from numpy import sin, pi # for nice math
from solver import solver
def F(t):
# Sinusoidal bumpy road
return A*sin(pi*t)
def s(u):
return k*(0.2*u + 1.5*u**3)
A = 0.25
k = 2
t = np.linspace(0, 100, 10001)
u, t = solver(I=0, V=0, m=2, b=0.5, s=s, F=F, t=t,
damping='quadratic')
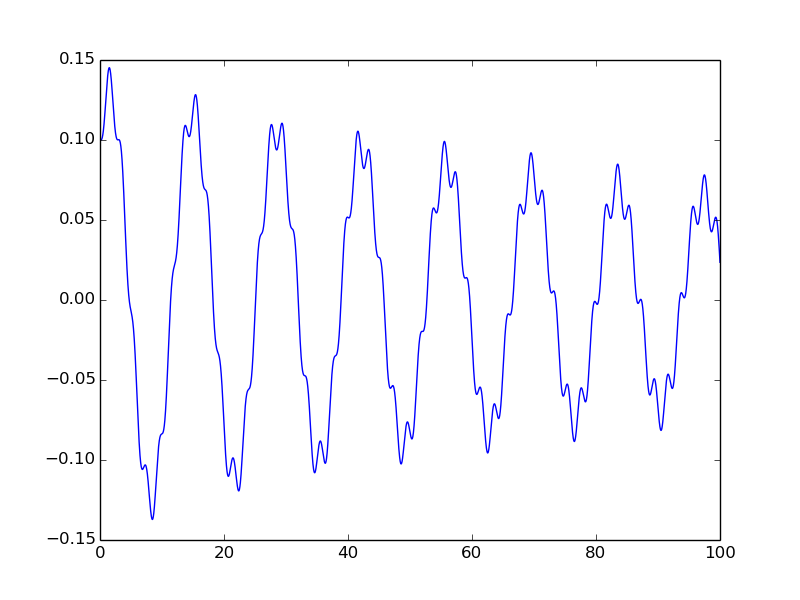
# Show u(t) as a curve plot
import matplotlib.pyplot as plt
plt.plot(t, u)
plt.show()
def f(u):
return k*u
Here,
u is a local variable,
which is accessible just inside in the functionk is a global variable, which must be initialized outside
the function prior to calling f__call__
for evaluating f(u)
class Spring:
def __init__(self, k):
self.k = k
def __call__(self, u):
return self.k*u
f = Spring(k)
# f looks like a function: can call f(0.2)
bumpy.dat.gz contains various road profiles \( h(x) \)
filename = 'bumpy.dat.gz'
url = 'http://hplbit.bitbucket.org/data/bumpy/bumpy.dat.gz'
import urllib
urllib.urlretrieve(url, filename)
h_data = np.loadtxt(filename) # read numpy array from file
x = h_data[0,:] # 1st column: x coordinates
h_data = h_data[1:,:] # other columns: h shapes
0 0.2 0.25 0.15
-0.1 0.15 0.2 0.15
>>> import numpy as np
>>> h_data = np.array([[0, 0.2, 0.25, 0.15],
[-0.1, 0.15, 0.2, 0.15]])
>>> h_data.shape # size of each dimension
(2, 4)
>>> h_data[0,:]
array([ 0. , 0.2 , 0.25, 0.15])
>>> h_data[:,0]
array([ 0. , -0.1])
>>> profile1 = h_data[1,:]
>>> profile1
array([-0.1 , 0.15, 0.2 , 0.15])
>>> h_data[1,1:3] # elements [1,1] [1,2]
array([ 0.15, 0.2 ])
def acceleration(h, x, v):
"""Compute 2nd-order derivative of h."""
# Method: standard finite difference aproximation
d2h = np.zeros(h.size)
dx = x[1] - x[0]
for i in range(1, h.size-1, 1):
d2h[i] = (h[i-1] - 2*h[i] + h[i+1])/dx**2
# Extraplolate end values from first interior value
d2h[0] = d2h[1]
d2h[-1] = d2h[-2]
a = d2h*v**2
return a
def acceleration_vectorized(h, x, v):
"""Compute 2nd-order derivative of h. Vectorized version."""
d2h = np.zeros(h.size)
dx = x[1] - x[0]
d2h[1:-1] = (h[:-2] - 2*h[1:-1] + h[2:])/dx**2
# Extraplolate end values from first interior value
d2h[0] = d2h[1]
d2h[-1] = d2h[-2]
a = d2h*v**2
return a
Use a list data to hold all input and output data
data = [x, t]
for i in range(h_data.shape[0]):
h = h_data[i,:] # extract a column
a = acceleration(h, x, v)
F = -m*a
u = solver(t=t, I=0, m=m, b=b, f=f, F=F)
data.append([h, F, u])
Parameters for bicycle conditions: \( m=60 \) kg, \( v=5 \) m/s, \( k=60 \) N/m, \( b=80 \) Ns/m
def bumpy_road(url=None, m=60, b=80, k=60, v=5):
"""
Simulate verticle vehicle vibrations.
========= ==============================================
variable description
========= ==============================================
url either URL of file with excitation force data,
or name of a local file
m mass of system
b friction parameter
k spring parameter
v (constant) velocity of vehicle
Return data (list) holding input and output data
[x, t, [h,F,u], [h,F,u], ...]
========= ==============================================
"""
# Download file (if url is not the name of a local file)
if url.startswith('http://') or url.startswith('file://'):
import urllib
filename = os.path.basename(url) # strip off path
urllib.urlretrieve(url, filename)
else:
# Check if url is the name of a local file
if not os.path.isfile(url):
print url, 'must be a URL or a filename'; sys.exit(1)
def bumpy_road(url=None, m=60, b=80, k=60, v=5):
...
h_data = np.loadtxt(filename) # read numpy array from file
x = h_data[0,:] # 1st column: x coordinates
h_data = h_data[1:,:] # other columns: h shapes
t = x/v # time corresponding to x
dt = t[1] - t[0]
def f(u):
return k*u
data = [x, t] # key input and output data (arrays)
for i in range(h_data.shape[0]):
h = h_data[i,:] # extract a column
a = acceleration(h, x, v)
F = -m*a
u = solver(t=t, I=0.2, m=m, b=b, f=f, F=F)
data.append([h, F, u])
return data
After calling
road_url = 'http://hplbit.bitbucket.org/data/bumpy/bumpy.dat.gz'
data = solve(url=road_url,
m=60, b=200, k=60, v=6)
data = rms(data)
the data array contains single arrays and triplets of arrays,
[x, t, [h,F,u], [h,F,u], ..., [h,F,u]]
This list, or any Python object, can be stored on file for later retrieval of the results, using pickling:
import cPickle
outfile = open('bumpy.res', 'w')
cPickle.dump(data, outfile)
outfile.close()
u_rms = []
for h, F, u in data[2:]:
u_rms.append(np.sqrt((1./len(u))*np.sum(u**2))
Or by the more compact list comprehension:
u_rms = [np.sqrt((1./len(u))*np.sum(u**2))
for h, F, u in data[2:]]
Suppose \( b \) is given on the command line:
Terminal> python bumpy.py 10
Code:
try:
b = float(sys.argv[1])
except IndexError:
b = 80 # default
Note:
sys.argv[1:]sys.argv[i] is a string, so float conversion is necessary
before calculationsWe can alternatively use option-value pairs on the command line:
Terminal> python bumpy.py --m 40 --b 280
Note:
--option valueargparse module for defining, reading, and accessing
option-value pairsargparse
def command_line_options():
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--m', '--mass', type=float,
default=60, help='mass of vehicle')
parser.add_argument('--k', '--spring', type=float,
default=60, help='spring parameter')
parser.add_argument('--b', '--damping', type=float,
default=80, help='damping parameter')
parser.add_argument('--v', '--velocity', type=float,
default=5, help='velocity of vehicle')
url = 'http://hplbit.bitbucket.org/data/bumpy/bumpy.dat.gz'
parser.add_argument('--roadfile', type=str,
default=url, help='filename/URL with road data')
args = parser.parse_args()
# Extract input parameters
m = args.m; k = args.k; b = args.b; v = args.v
url = args.roadfile
return url, m, b, k, v
Terminal> python bumpy.py --velocity 10
The rest of the parameters have their default values
Plot
Loading pickled results in file:
import cPickle
outfile = open('bumpy.res', 'r')
data = cPickle.load(outfile)
outfile.close()
x, t = data[0:2]
Recall list data:
[x, t, [h,F,u], [h,F,u], ..., [h,F,u]]
Further, for convenience (and Matlab-like code):
from numpy import *
from matplotlib.pyplot import *
Display only the last portion of time series:
indices = t >= t_s # True/False boolean array
t = t[indices] # fetch the part of t for which t > t_s
x = x[indices] # fetch the part of x for which t > t_s
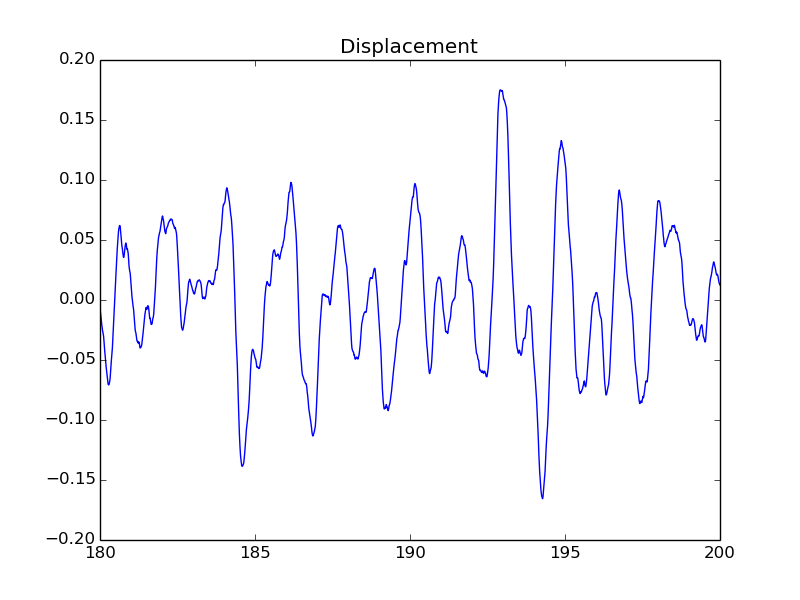
Plotting \( u \):
figure()
realization = 1
u = data[2+realization][2][indices]
plot(t, u)
title('Displacement')
Note: data[2+realization] is a triplet [h,F,u]

v = zeros_like(u) # same length and data type as u
dt = t[1] - t[0] # time step
for i in range(1,u.size-1):
v[i] = (u[i+1] - u[i-1])/(2*dt)
v[0] = (u[1] - u[0])/dt
v[N] = (u[N] - u[N-1])/dt
Vectorized version:
v = zeros_like(u)
v[1:-1] = (u[2:] - u[:-2])/(2*dt)
v[0] = (u[1] - u[0])/dt
v[-1] = (u[-1] - u[-2])/dt
IPython has the convenient %timeit feature for measuring CPU time:
In [1]: from numpy import zeros
In [2]: N = 1000000
In [3]: u = zeros(N)
In [4]: %timeit v = u[2:] - u[:-2]
1 loops, best of 3: 5.76 ms per loop
In [5]: v = zeros(N)
In [6]: %timeit for i in range(1,N-1): v[i] = u[i+1] - u[i-1]
1 loops, best of 3: 836 ms per loop
In [7]: 836/5.76
Out[20]: 145.13888888888889
145 times faster!
The spectrum of a discrete function \( u(t) \):
def frequency_analysis(u, t):
A = fft(u)
A = 2*A
dt = t[1] - t[0]
N = t.size
freq = arange(N/2, dtype=float)/N/dt
A = abs(A[0:freq.size])/N
# Remove small high frequency part
tol = 0.05*A.max()
for i in xrange(len(A)-1, 0, -1):
if A[i] > tol:
break
return freq[:i+1], A[:i+1]
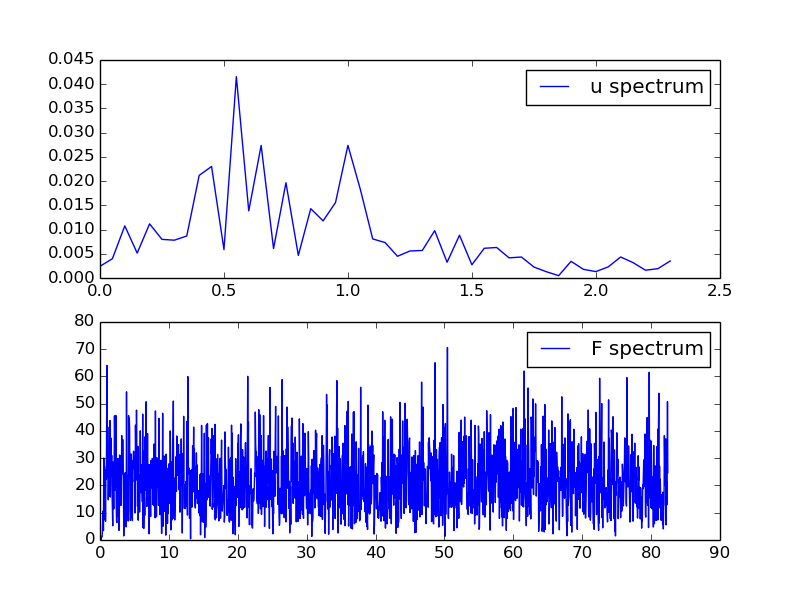
figure()
u = data[3][2][indices] # 2nd realization of u
f, A = frequency_analysis(u, t)
plot(f, A)
title('Spectrum of u')
Run through all the 3-lists [h, F, u] and plot
these arrays:
for realization in range(len(data[2:])):
h, F, u = data[2+realization]
h = h[indices]; F = F[indices]; u = u[indices]
figure()
subplot(3, 1, 1)
plot(x, h, 'g-')
legend(['h %d' % realization])
hmax = (abs(h.max()) + abs(h.min()))/2
axis([x[0], x[-1], -hmax*5, hmax*5])
xlabel('distance'); ylabel('height')
subplot(3, 1, 2)
plot(t, F)
legend(['F %d' % realization])
xlabel('t'); ylabel('acceleration')
subplot(3, 1, 3)
plot(t, u, 'r-')
legend(['u %d' % realization])
xlabel('t'); ylabel('displacement')
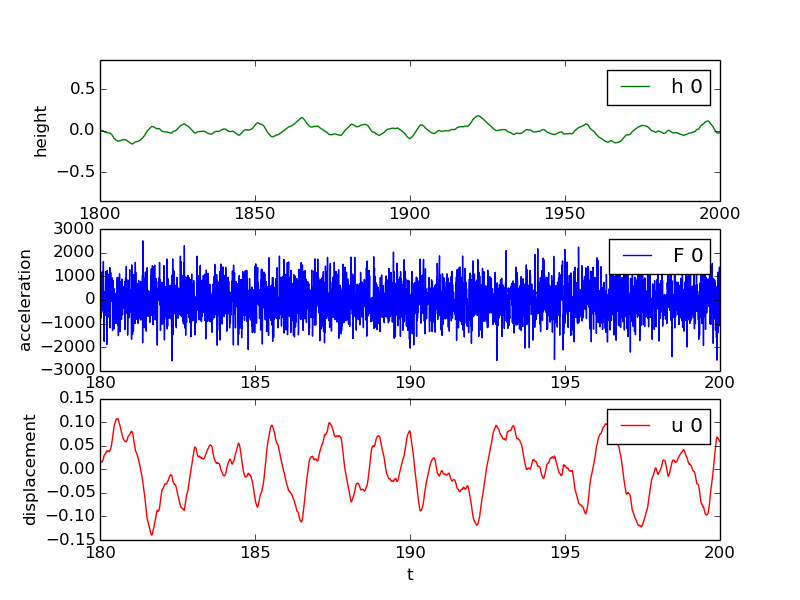
See explore.py

SymPy can do exact differentiation, integration, equation solving, ...
>>> import sympy as sp
>>> x, a = sp.symbols('x a') # Define mathematical symbols
>>> Q = a*x**2 - 1 # Quadratic function
>>> dQdx = sp.diff(Q, x) # Differentiate wrt x
>>> dQdx
2*a*x
>>> Q2 = sp.integrate(dQdx, x) # Integrate (no constant)
>>> Q2
a*x**2
>>> Q2 = sp.integrate(Q, (x, 0, a)) # Definite integral
>>> Q2
a**4/3 - a
>>> roots = sp.solve(Q, x) # Solve Q = 0 wrt x
>>> roots
[-sqrt(1/a), sqrt(1/a)]
Convert a SymPy expression Q into
a Python function Q(x, a):
>>> Q = sp.lambdify([x, a], Q) # Turn Q into Py func.
>>> Q(x=2, a=3) # 3*2**2 - 1 = 11
11
This Q(x, a) function can be used for numerical computing
Modern test frameworks:
Use pytest, stay away from classical unittest
def halve(x):
"""Return half of x."""
return x/2.0
def test_halve():
x = 4
expected = 2
computed = halve(x)
# Compare real numbers using tolerance
tol = 1E-14
diff = abs(computed - expected)
assert diff < tol
Note:
test_*assert on a boolean expression for passed test
Show that \( u=I + Vt + qt^2 \) solves the discrete equations exactly for linear damping and with \( q=0 \) for quadratic damping
def lhs_eq(t, m, b, s, u, damping='linear'):
"""Return lhs of differential equation as sympy expression."""
v = sm.diff(u, t)
d = b*v if damping == 'linear' else b*v*sm.Abs(v)
return m*sm.diff(u, t, t) + d + s(u)
Fit source term in differential equation to any chosen \( u(t) \):
t = sm.Symbol('t')
q = 2 # arbitrary constant
u_chosen = I + V*t + q*t**2 # sympy expression
F_term = lhs_eq(t, m, b, s, u_chosen, 'linear')
import sympy as sm
def test_solver():
"""Verify linear/quadratic solution."""
# Set input data for the test
I = 1.2; V = 3; m = 2; b = 0.9; k = 4
s = lambda u: k*u
T = 2
dt = 0.2
N = int(round(T/dt))
time_points = np.linspace(0, T, N+1)
# Test linear damping
t = sm.Symbol('t')
q = 2 # arbitrary constant
u_exact = I + V*t + q*t**2 # sympy expression
F_term = lhs_eq(t, m, b, s, u_exact, 'linear')
print 'Fitted source term, linear case:', F_term
F = sm.lambdify([t], F_term)
u, t_ = solver(I, V, m, b, s, F, time_points, 'linear')
u_e = sm.lambdify([t], u_exact, modules='numpy')
error = abs(u_e(t_) - u).max()
tol = 1E-13
assert error < tol
def test_solver():
...
# Test quadratic damping: u_exact must be linear
u_exact = I + V*t
F_term = lhs_eq(t, m, b, s, u_exact, 'quadratic')
print 'Fitted source term, quadratic case:', F_term
F = sm.lambdify([t], F_term)
u, t_ = solver(I, V, m, b, s, F, time_points, 'quadratic')
u_e = sm.lambdify([t], u_exact, modules='numpy')
error = abs(u_e(t_) - u).max()
assert error < tol
Examine all subdirectories test* for test_*.py files:
Terminal> py.test -s
====================== test session starts =======================
...
collected 3 items
tests/test_bumpy.py .
Fitted source term, linear case: 8*t**2 + 15.6*t + 15.5
Fitted source term, quadratic case: 12*t + 12.9
testing solver
testing solver_linear_damping_wrapper
==================== 3 passed in 0.40 seconds ====================
Test a single file:
Terminal> py.test -s tests/test_bumpy.py
...
if __name__ == '__main__':
<statements in the main program>
import module1
from module2 import somefunc1, somefunc2
def myfunc1(...):
...
def myfunc2(...):
...
if __name__ == '__main__':
<statements in the main program>
Import everything from the previous module:
from mymod import *
This imports
module1, somefunc1, somefunc2 (global names in mymod)myfunc1, myfunc2 (global functions in mymod)