The section Understanding the Forward Euler method describes a geometric interpretation of the Forward Euler method. This exercise will demonstrate the geometric construction of the solution in detail. Consider the differential equation \( u'=u \) with \( u(0)=1 \). We use time steps \( \Delta t = 1 \).
a) Start at \( t=0 \) and draw a straight line with slope \( u'(0)=u(0)=1 \). Go one time step forward to \( t=\Delta t \) and mark the solution point on the line.
b) Draw a straight line through the solution point \( (\Delta t, u^1) \) with slope \( u'(\Delta t)=u^1 \). Go one time step forward to \( t=2\Delta t \) and mark the solution point on the line.
c) Draw a straight line through the solution point \( (2\Delta t, u^2) \) with slope \( u'(2\Delta t)=u^2 \). Go one time step forward to \( t=3\Delta t \) and mark the solution point on the line.
d) Set up the Forward Euler scheme for the problem \( u'=u \). Calculate \( u^1 \), \( u^2 \), and \( u^3 \). Check that the numbers are the same as obtained in a)-c).
Filename: ForwardEuler_geometric_solution.py.
The purpose of this exercise is to
make a file test_ode_FE.py that makes use of the ode_FE
function in the file ode_FE.py and automatically verifies the
implementation of ode_FE.
a)
The solution computed by hand in Exercise 4.1: Geometric construction of the Forward Euler method can be
used as a reference solution. Make a function test_ode_FE_1()
that calls ode_FE to compute
three time steps in the problem \( u'=u \), \( u(0)=1 \), and compare the
three values \( u^1 \), \( u^2 \), and \( u^3 \) with the values obtained in
Exercise 4.1: Geometric construction of the Forward Euler method.
b)
The test in a) can be made more general using the fact
that if \( f \) is linear in \( u \) and does not depend on \( t \), i.e., we
have \( u'=ru \), for
some constant \( r \), the Forward Euler method has a closed form solution
as outlined in the section Derivation of the model: \( u^n=U_0(1+r\Delta t)^n \).
Use this result to construct a test function test_ode_FE_2() that
runs a number of steps in ode_FE and compares the computed
solution with the listed formula for \( u^n \).
Filename: test_ode_FE.py.
a)
A 2nd-order Runge-Kutta method, also known has Heun's method,
is derived in the section The 2nd-order Runge-Kutta method (or Heun's method). Make a function
ode_Heun(f, U_0, dt, T) (as a counterpart to ode_FE(f, U_0, dt, T)
in ode_FE.py) for solving a scalar ODE problem \( u'=f(u,t) \),
\( u(0)=U_0 \), \( t\in (0,T] \), with
this method using a time step size \( \Delta t \).
b)
Solve the simple ODE problem \( u'=u \), \( u(0)=1 \), by the ode_Heun and
the ode_FE function. Make
a plot that compares Heun's method and the Forward Euler method
with the exact solution \( u(t)=e^t \) for \( t\in [0,6] \). Use a
time step \( \Delta t = 0.5 \).
c) For the case in b), find through experimentation the largest value of \( \Delta t \) where the exact solution and the numerical solution by Heun's method cannot be distinguished visually. It is of interest to see how far off the curve the Forward Euler method is when Heun's method can be regarded as "exact" (for visual purposes).
Filename: ode_Heun.py.
Compute the numerical solution of the logistic equation for a set of repeatedly halved time steps: \( \Delta t_k = 2^{-k}\Delta t \), \( k=0,1,\ldots \). Plot the solutions corresponding to the last two time steps \( \Delta t_{k} \) and \( \Delta t_{k-1} \) in the same plot. Continue doing this until you cannot visually distinguish the two curves in the plot. Then one has found a sufficiently small time step.
Hint.
Extend the logistic.py file. Introduce a loop over \( k \), write out
\( \Delta t_k \), and ask the
user if the loop is to be continued.
Filename: logistic_dt.py.
Repeat Exercise 4.4: Find an appropriate time step; logistic model for the SIR model.
Hint.
Import the ode_FE function from the ode_system_FE module
and make a modified demo_SIR function that has a loop
over repeatedly halved time steps. Plot \( S \), \( I \), and \( R \)
versus time for the two last time step sizes in the same plot.
Filename: SIR_dt.py.
In the SIRV model with time-dependent vaccination from the section Discontinuous coefficients: a vaccination campaign, we want to test the effect of an adaptive vaccination campaign where vaccination is offered as long as half of the population is not vaccinated. The campaign starts after \( \Delta \) days. That is, \( p=p_0 \) if \( V < \frac{1}{2}(S^0+I^0) \) and \( t>\Delta \) days, otherwise \( p=0 \).
Demonstrate the effect of this vaccination policy: choose \( \beta \), \( \gamma \), and \( \nu \) as in the section Discontinuous coefficients: a vaccination campaign, set \( p=0.001 \), \( \Delta =10 \) days, and simulate for 200 days.
Hint.
This discontinuous \( p(t) \) function is easiest implemented as a
Python function containing the indicated if test.
You may use the file SIRV1.py
as starting point, but note that it implements a time-dependent
\( p(t) \) via an array.
Filename: SIRV_p_adapt.py.
We consider the SIRV model from the section Incorporating vaccination, but now the effect of vaccination is time-limited. After a characteristic period of time, \( \pi \), the vaccination is no more effective and individuals are consequently moved from the V to the S category and can be infected again. Mathematically, this can be modeled as an average leakage \( -\pi^{-1}V \) from the V category to the S category (i.e., a gain \( \pi^{-1}V \) in the latter). Write up the complete model, implement it, and rerun the case from the section Incorporating vaccination with various choices of parameters to illustrate various effects.
Filename: SIRV1_V2S.py.
Consider the file osc_FE.py implementing the Forward Euler
method for the oscillating system model
(71)-(72).
The osc_FE.py is what we often refer to as a flat program,
meaning that it is just one main program with no functions.
To easily reuse the numerical computations in other contexts,
place the part that produces the numerical solution (allocation of arrays,
initializing the arrays at time zero, and the time loop) in
a function osc_FE(X_0, omega, dt, T), which returns u, v, t.
Place the particular
computational example in osc_FE.py in a function
demo().
Construct the file osc_FE_func.py such that the
osc_FE function can easily be reused
in other programs.
In Python, this means that osc_FE_func.py is a module that can
be imported in other programs.
The requirement of a module is that there should be no main program,
except in the test block.
You must therefore
call demo from a test block (i.e., the block
after if __name__ == '__main__').
Filename: osc_FE_func.py.
Solve the system (71)-(72)
using the general solver ode_FE in the file ode_system_FE.py
described in the section Programming the numerical method; the general case. Program the ODE system
and the call to the ode_FE function in a separate file
osc_ode_FE.py.
Equip this file with a test function that reads a file with correct
\( u \) values and compares these with those computed by the ode_FE
function. To find correct \( u \) values, modify the program
osc_FE.py to dump the u array to file, run osc_FE.py, and
let the test function read the reference results from that file.
Filename: osc_ode_FE.py.
a)
Make a function osc_energy(u, v, omega) for returning the potential and
kinetic energy of an oscillating system described by
(71)-(72).
The potential energy is taken as \( \frac{1}{2}\omega^2u^2 \) while
the kinetic energy is \( \frac{1}{2}v^2 \). (Note that these expressions
are not exactly the physical potential and kinetic energy, since
these would be \( \frac{1}{2}mv^2 \) and \( \frac{1}{2}ku^2 \) for a model
\( mx'' + kx=0 \).)
Place the osc_energy in a separate file osc_energy.py
such that the function can be called from other functions.
b)
Add a call to osc_energy in the programs osc_FE.py and
osc_EC.py and plot the sum of the kinetic and potential energy.
How does the total energy develop for the Forward Euler and the
Euler-Cromer schemes?
Filenames: osc_energy.py, osc_FE_energy.py, osc_EC_energy.py.
We consider the ODE problem \( N'(t)=rN(t) \), \( N(0)=N_0 \). At some time, \( t_n=n\Delta t \), we can approximate the derivative \( N'(t_n) \) by a backward difference, see Figure 38: $$ N'(t_n)\approx \frac{N(t_n) - N(t_n-\Delta t)}{\Delta t} = \frac{N^n - N^{n-1}}{\Delta t},$$ which leads to $$ \frac{N^n - N^{n-1}}{\Delta t} = rN^n\thinspace,$$ called the Backward Euler scheme.
a) Find an expression for the \( N^n \) in terms of \( N^{n-1} \) and formulate an algorithm for computing \( N^n \), \( n=1,2,\ldots,N_t \).
b)
Implement the algorithm in a) in a function growth_BE(N_0, dt, T)
for solving \( N'=rN \), \( N(0)=N_0 \), \( t\in (0,T] \), with time step \( \Delta t \) (dt).
c)
Implement the Forward Euler scheme in a function growth_FE(N_0, dt, T)
as described in b).
d) Compare visually the solution produced by the Forward and Backward Euler schemes with the exact solution when \( r=1 \) and \( T=6 \). Make two plots, one with \( \Delta t = 0.5 \) and one with \( \Delta t=0.05 \).
Filename: growth_BE.py.
It is recommended to do Exercise 4.11: Use a Backward Euler scheme for population growth prior to the present one. Here we look at the same population growth model \( N'(t)=rN(t) \), \( N(0)=N_0 \). The time derivative \( N'(t) \) can be approximated by various types of finite differences. Exercise 4.11: Use a Backward Euler scheme for population growth considers a backward difference (Figure 38), while the section Numerical solution explained the forward difference (Figure 21). A centered difference is more accurate than a backward or forward difference: $$ N'(t_n+\frac{1}{2}\Delta t)\approx\frac{N(t_n+\Delta t)-N(t_n)}{\Delta t}= \frac{N^{n+1}-N^n}{\Delta t}\thinspace .$$ This type of difference, applied at the point \( t_{n+\frac{1}{2}}=t_n + \frac{1}{2}\Delta t \), is illustrated geometrically in Figure 39.
a) Insert the finite difference approximation in the ODE \( N'=rN \) and solve for the unknown \( N^{n+1} \), assuming \( N^n \) is already computed and hence known. The resulting computational scheme is often referred to as a Crank-Nicolson scheme.
b)
Implement the algorithm in a) in a function growth_CN(N_0, dt, T)
for solving \( N'=rN \), \( N(0)=N_0 \), \( t\in (0,T] \), with time step \( \Delta t \) (dt).
c) Make plots for comparing the Crank-Nicolson scheme with the Forward and Backward Euler schemes in the same test problem as in Exercise 4.11: Use a Backward Euler scheme for population growth.
Filename: growth_CN.py.
The Taylor series around a point \( x=a \) can for a function \( f(x) \) be written $$ \begin{align*} f(x) &= f(a) + \frac{d}{dx}f(a)(x-a) + \frac{1}{2!}\frac{d^2}{dx^2}f(a)(x-a)^2 \\ &\quad + \frac{1}{3!}\frac{d^3}{dx^3}f(a)(x-a)^3 + \ldots\\ & = \sum_{i=0}^\infty \frac{1}{i!}\frac{d^i}{dx^i}f(a)(x-a)^i\thinspace . \end{align*} $$ For a function of time, as addressed in our ODE problems, we would use \( u \) instead of \( f \), \( t \) instead of \( x \), and a time point \( t_n \) instead of \( a \): $$ \begin{align*} u(t) &= u(t_n) + \frac{d}{dt}u(t_n)(t-t_n) + \frac{1}{2!}\frac{d^2}{dt^2}u(t_n)(t-t_n)^2\\ &\quad + \frac{1}{3!}\frac{d^3}{dt^3}u(t_n)(t-t_n)^3 + \ldots\\ & = \sum_{i=0}^\infty \frac{1}{i!}\frac{d^i}{dt^i}u(t_n)(t-t_n)^i\thinspace . \end{align*} $$
a) A forward finite difference approximation to the derivative \( f'(a) \) reads $$ u'(t_n) \approx \frac{u(t_n+\Delta t)- u(t_n)}{\Delta t}\thinspace .$$ We can justify this formula mathematically through Taylor series. Write up the Taylor series for \( u(t_n+\Delta t) \) (around \( t=t_n \), as given above), and then solve the expression with respect to \( u'(t_n) \). Identify, on the right-hand side, the finite difference approximation and an infinite series. This series is then the error in the finite difference approximation. If \( \Delta t \) is assumed small (i.e. \( \Delta t < < 1 \)), \( \Delta t \) will be much larger than \( \Delta t^2 \), which will be much larger than \( \Delta t^3 \), and so on. The leading order term in the series for the error, i.e., the error with the least power of \( \Delta t \) is a good approximation of the error. Identify this term.
b) Repeat a) for a backward difference: $$ u'(t_n) \approx \frac{u(t_n)- u(t_n-\Delta t)}{\Delta t}\thinspace .$$ This time, write up the Taylor series for \( u(t_n-\Delta t) \) around \( t_n \). Solve with respect to \( u'(t_n) \), and identify the leading order term in the error. How is the error compared to the forward difference?
c) A centered difference approximation to the derivative, as explored in Exercise 4.12: Use a Crank-Nicolson scheme for population growth, can be written $$ u'(t_n+\frac{1}{2}\Delta t) \approx \frac{u(t_n+\Delta t)- u(t_n)}{\Delta t}\thinspace .$$ Write up the Taylor series for \( u(t_n) \) around \( t_n+\frac{1}{2}\Delta t \) and the Taylor series for \( u(t_n+\Delta t) \) around \( t_n+\frac{1}{2}\Delta t \). Subtract the two series, solve with respect to \( u'(t_n+\frac{1}{2}\Delta t) \), identify the finite difference approximation and the error terms on the right-hand side, and write up the leading order error term. How is this term compared to the ones for the forward and backward differences?
d) Can you use the leading order error terms in a)-c) to explain the visual observations in the numerical experiment in Exercise 4.12: Use a Crank-Nicolson scheme for population growth?
e) Find the leading order error term in the following standard finite difference approximation to the second-order derivative: $$ u''(t_n) \approx \frac{u(t_n+\Delta t)- 2u(t_n) + u(t_n-\Delta t)}{\Delta t}\thinspace .$$
Hint. Express \( u(t_n\pm \Delta t) \) via Taylor series and insert them in the difference formula.
Filename: Taylor_differences.pdf.
Consider (71)-(72) modeling an oscillating engineering system. This \( 2\times 2 \) ODE system can be solved by the Backward Euler scheme, which is based on discretizing derivatives by collecting information backward in time. More specifically, \( u'(t) \) is approximated as $$ u'(t) \approx \frac{u(t) - u(t-\Delta t)}{\Delta t}\thinspace .$$ A general vector ODE \( u'=f(u,t) \), where \( u \) and \( f \) are vectors, can use this approximation as follows: $$ \frac{u^{n} - u^{n-1}}{\Delta t} = f(u^n,t_n),$$ which leads to an equation for the new value \( u^n \): $$ u^n -\Delta tf(u^n,t_n) = u^{n-1}\thinspace .$$ For a general \( f \), this is a system of nonlinear algebraic equations.
However, the ODE (71)-(72) is linear, so a Backward Euler scheme leads to a system of two algebraic equations for two unknowns: $$ \begin{align} u^{n} - \Delta t v^{n} &= u^{n-1}, \tag{112}\\ v^{n} + \Delta t \omega^2 u^{n} &= v^{n-1} \tag{113} \thinspace . \end{align} $$
a) Solve the system for \( u^n \) and \( v^n \).
b) Implement the found formulas for \( u^n \) and \( v^n \) in a program for computing the entire numerical solution of (71)-(72).
c) Run the program with a \( \Delta t \) corresponding to 20 time steps per period of the oscillations (see the section Programming the numerical method; the special case for how to find such a \( \Delta t \)). What do you observe? Increase to 2000 time steps per period. How much does this improve the solution?
Filename: osc_BE.py.
While the Forward Euler method applied to oscillation problems \( u''+\omega^2u=0 \) gives growing amplitudes, the Backward Euler method leads to significantly damped amplitudes.
Make a program that computes the solution of the SIR model from the section Spreading of a flu both by the Forward Euler method and by Heun's method (or equivalently: the 2nd-order Runge-Kutta method) from the section The 2nd-order Runge-Kutta method (or Heun's method). Compare the two methods in the simulation case from the section Programming the numerical method; the special case. Make two comparison plots, one for a large and one for a small time step. Experiment to find what "large" and "small" should be: the large one gives significant differences, while the small one lead to very similar curves.
Filename: SIR_Heun.py.
Solve $$ u' = -au + b,\quad u(0)=U_0,\quad t\in (0,T]$$ by the Odespy software. Let the problem parameters \( a \) and \( b \) be arguments to the right-hand side function that specifies the ODE to be solved. Plot the solution for the case when \( a=2 \), \( b=1 \), \( T=6/a \), and we use 100 time intervals in \( [0,T] \).
Filename: odespy_demo.py.
Write the ODE \( u'' + \omega^2u=0 \) as a system of two first-order
ODEs and discretize these with backward differences as illustrated
in Figure 38. The resulting method is referred to as
a Backward Euler scheme. Identify the matrix and right-hand side
of the linear system that has to be solved at each time level.
Implement the method, either from scratch yourself or using
Odespy (the name is odespy.BackwardEuler).
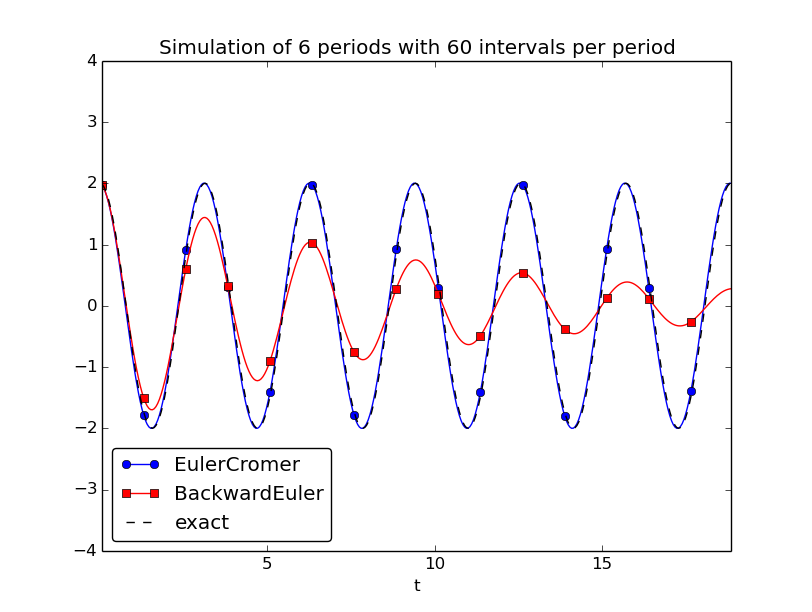
Demonstrate that contrary to a Forward Euler scheme, the Backward
Euler scheme leads to significant non-physical damping. The figure
below shows that even with 60 time steps per period, the results
after a few periods are useless:

Filename: osc_BE.py.
Derive a Forward Euler method for the ODE system (96)-(97). Compare the method with the Euler-Cromer scheme for the sliding friction problem from the section Spring-mass system with sliding friction:
osc_FE_general.py.
Assume that the initial condition on \( u' \) is nonzero in the finite difference method from the section A finite difference method; undamped, linear case: \( u'(0)=V_0 \). Derive the special formula for \( u^1 \) in this case.
Filename: ic_with_V_0.pdf.