Study Guide: Finite difference methods for wave motion

Table of contents

Finite difference methods for waves on a string
      The complete initial-boundary value problem
      Input data in the problem
      Demo of a vibrating string (\( C=0.8 \))
      Demo of a vibrating string (\( C=1.0012 \))
      Step 1: Discretizing the domain
      The discrete solution
      Step 2: Fulfilling the equation at the mesh points
      Step 3: Replacing derivatives by finite differences
      Step 3: Algebraic version of the PDE
      Step 3: Algebraic version of the initial conditions
      Step 4: Formulating a recursive algorithm
      The Courant number
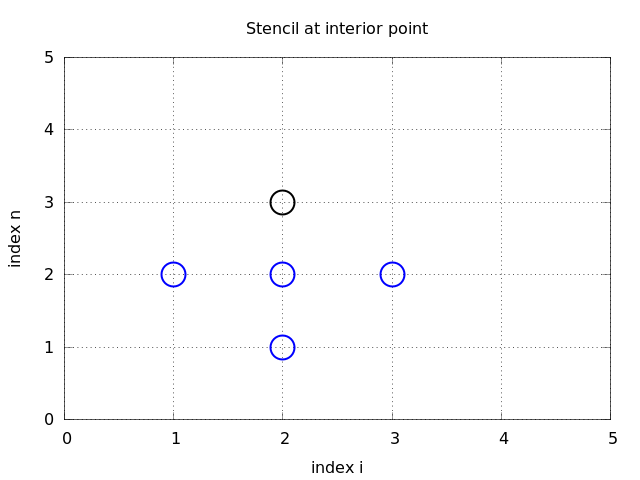
      The finite difference stencil
      The stencil for the first time level
      The algorithm
      Moving finite difference stencil
      Sketch of an implementation (1)
      PDE solvers should save memory
      Sketch of an implementation (2)
Verification
      A slightly generalized model problem
      Discrete model for the generalized model problem
      Modified equation for the first time level
      Using an analytical solution of physical significance
      Manufactured solution: principles
      Manufactured solution: example
      Testing a manufactured solution
      Constructing an exact solution of the discrete equations
      Analytical work with the PDE problem
      Analytical work with the discrete equations (1)
      Analytical work with the discrete equations (1)
      Testing with the exact discrete solution
Implementation
      The algorithm
      What do to with the solution?
      Making a solver function
      Verification: exact quadratic solution
      Visualization: animating \( u(x,t) \)
      Making movie files
      Running a case
      Implementation of the case
      Resulting movie for \( C=0.8 \)
      The benefits of scaling
Vectorization
      Operations on slices of arrays
      Test the understanding
      Vectorization of finite difference schemes (1)
      Vectorization of finite difference schemes (2)
      Vectorized implementation in the solver function
      Verification of the vectorized version
      Efficiency measurements
Generalization: reflecting boundaries
      Neumann boundary condition
      Discretization of derivatives at the boundary (1)
      Discretization of derivatives at the boundary (2)
      Visualization of modified boundary stencil
      Implementation of Neumann conditions
      Moving finite difference stencil
      Index set notation
      Index set notation in code
      Index sets in action (1)
      Index sets in action (2)
      Alternative implementation via ghost cells
      Implementation of ghost cells (1)
      Implementation of ghost cells (2)
Generalization: variable wave velocity
      The model PDE with a variable coefficient
      Discretizing the variable coefficient (1)
      Discretizing the variable coefficient (2)
      Discretizing the variable coefficient (3)
      Computing the coefficient between mesh points
      Discretization of variable-coefficient wave equation in operator notation
      Neumann condition and a variable coefficient
      Implementation of variable coefficients
      A more general model PDE with variable coefficients
      Generalization: damping
Building a general 1D wave equation solver
      Collection of initial conditions
Finite difference methods for 2D and 3D wave equations
      Examples on wave equations written out in 2D/3D
      Boundary and initial conditions
      Example: 2D propagation of Gaussian function
      Mesh
      Discretization
      Special stencil for the first time step
      Variable coefficients (1)
      Variable coefficients (2)
      Neumann boundary condition in 2D
Implementation of 2D/3D problems
      Algorithm
      Scalar computations: mesh
      Scalar computations: arrays
      Scalar computations: initial condition
      Scalar computations: primary stencil
      Vectorized computations: mesh coordinates
      Vectorized computations: stencil
      Verification: quadratic solution (1)
      Verification: quadratic solution (2)
Migrating loops to Cython
      Declaring variables and annotating the code
      Cython version of the functions
      Visual inspection of the C translation
      Building the extension module
      Calling the Cython function from Python
Migrating loops to Fortran
      The Fortran subroutine
      Building the Fortran module with f2py
      How to avoid array copying
      Efficiency of translating to Fortran
Migrating loops to C via Cython
      The C code
      The Cython interface file
      Building the extension module
Migrating loops to C via f2py
      The C code and the Fortran interface file
      Building the extension module
      Migrating loops to C++ via f2py
Analysis of the difference equations
      Properties of the solution of the wave equation
      Demo of the splitting of \( I(x) \) into two waves
      Effect of variable wave velocity
      What happens here?
      Representation of waves as sum of sine/cosine waves
      Analysis of the finite difference scheme
      Preliminary results
      Numerical wave propagation (1)
      Numerical wave propagation (2)
      Numerical wave propagation (3)
      Why \( C\leq 1 \) is a stability criterion
      Numerical dispersion relation
      The special case \( C=1 \)
      Computing the error in wave velocity
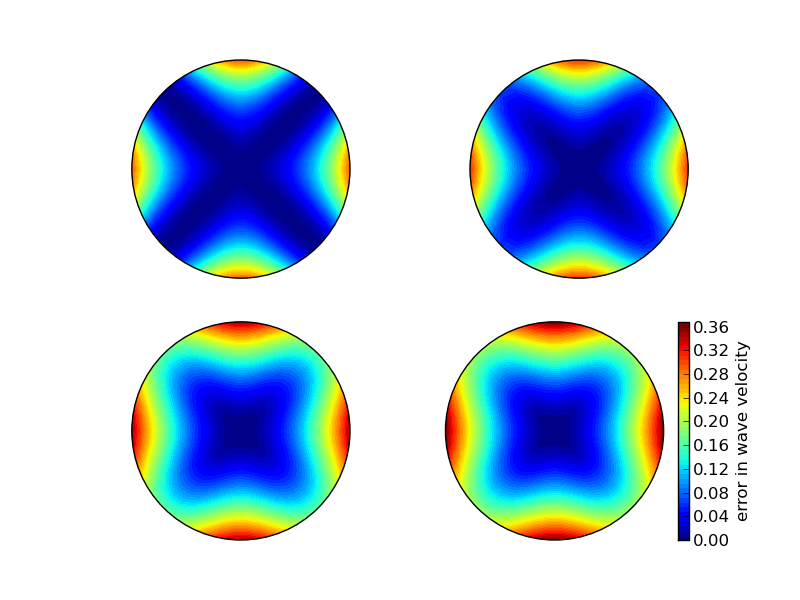
      Visualizing the error in wave velocity
      Taylor expanding the error in wave velocity
      Example on effect of wrong wave velocity (1)
      Example on effect of wrong wave velocity (1)
      Extending the analysis to 2D (and 3D)
      Discrete wave components in 2D
      Stability criterion in 2D
      Stability criterion in 3D
      Numerical dispersion relation in 2D (1)
      Numerical dispersion relation in 2D (2)
      Numerical dispersion relation in 2D (3)

Finite difference methods for waves on a string

Waves on a string can be modeled by the wave equation

$$ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} $$

\( u(x,t) \) is the displacement of the string

Demo of waves on a string.

The complete initial-boundary value problem

$$ \begin{align} \frac{\partial^2 u}{\partial t^2} &= c^2 \frac{\partial^2 u}{\partial x^2}, \quad &x\in (0,L),\ t\in (0,T] \label{wave:pde1}\\ u(x,0) &= I(x), \quad &x\in [0,L] \label{wave:pde1:ic:u}\\ \frac{\partial}{\partial t}u(x,0) &= 0, \quad &x\in [0,L] \label{wave:pde1:ic:ut}\\ u(0,t) & = 0, \quad &t\in (0,T] \label{wave:pde1:bc:0}\\ u(L,t) & = 0, \quad &t\in (0,T] \label{wave:pde1:bc:L} \end{align} $$

Input data in the problem

• Initial condition \( u(x,0)=I(x) \): initial string shape
• Initial condition \( u_t(x,0)=0 \): string starts from rest
• \( c=\sqrt{T/\varrho} \): velocity of waves on the string
• (\( T \) is the tension in the string, \( \varrho \) is density of the string)
• Two boundary conditions on \( u \): \( u=0 \) means fixed ends (no displacement)

• \( u_{tt} \) in the PDE: two initial conditions, on \( u \) and \( u_t \)
• \( u_{t} \) (and no \( u_{tt} \)) in the PDE: one initial conditions, on \( u \)
• \( u_{xx} \) in the PDE: one boundary condition on \( u \) at each boundary point

Demo of a vibrating string (\( C=0.8 \))

• Our numerical method is sometimes exact (!)
• Our numerical method is sometimes subject to serious non-physical effects

Demo of a vibrating string (\( C=1.0012 \))

Ooops!

Step 1: Discretizing the domain

Mesh in time:

$$ \begin{equation} 0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T \end{equation} $$

Mesh in space:

$$ \begin{equation} 0 = x_0 < x_1 < x_2 < \cdots < x_{N_x-1} < x_{N_x} = L \end{equation} $$

Uniform mesh with constant mesh spacings \( \Delta t \) and \( \Delta x \):

$$ \begin{equation} x_i = i\Delta x,\ i=0,\ldots,N_x,\quad t_i = n\Delta t,\ n=0,\ldots,N_t \end{equation} $$

The discrete solution

• The numerical solution is a mesh function: \( u_i^n \approx \uex(x_i,t_n) \)
• Finite difference stencil (or scheme): equation for \( u^n_i \) involving neighboring space-time points

Step 2: Fulfilling the equation at the mesh points

Let the PDE be satisfied at all interior mesh points:

$$ \begin{equation} \frac{\partial^2}{\partial t^2} u(x_i, t_n) = c^2\frac{\partial^2}{\partial x^2} u(x_i, t_n), \label{wave:pde1:step2} \end{equation} $$ for \( i=1,\ldots,N_x-1 \) and \( n=1,\ldots,N_t-1 \).

For \( n=0 \) we have the initial conditions \( u=I(x) \) and \( u_t=0 \), and at the boundaries \( i=0,N_x \) we have the boundary condition \( u=0 \).

Step 3: Replacing derivatives by finite differences

Widely used finite difference formula for the second-order derivative:

$$ \frac{\partial^2}{\partial t^2}u(x_i,t_n)\approx \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2}= [D_tD_t u]^n_i$$

and

$$ \frac{\partial^2}{\partial x^2}u(x_i,t_n)\approx \frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2} = [D_xD_x u]^n_i $$

Step 3: Algebraic version of the PDE

Replace derivatives by differences:

$$ \begin{equation} \frac{u_i^{n+1} - 2u_i^n + u^{n-1}_i}{\Delta t^2} = c^2\frac{u_{i+1}^{n} - 2u_i^n + u^{n}_{i-1}}{\Delta x^2}, \label{wave:pde1:step3b} \end{equation} $$

In operator notation:

$$ \begin{equation} [D_tD_t u = c^2 D_xD_x]^{n}_i \label{wave:pde1:step3a} \end{equation} $$

Step 3: Algebraic version of the initial conditions

• Need to replace the derivative in the initial condition \( u_t(x,0)=0 \) by a finite difference approximation
• The differences for \( u_{tt} \) and \( u_{xx} \) have second-order accuracy
• Use a centered difference for \( u_t(x,0) \)

The other initial condition \( u(x,0)=I(x) \) can be computed by

$$ u_i^0 = I(x_i),\quad i=0,\ldots,N_x$$

Step 4: Formulating a recursive algorithm

• Nature of the algorithm: compute \( u \) in space at \( t=\Delta t, 2\Delta t, 3\Delta t,... \)
• Three time levels are involved in the general discrete equation: \( n+1 \), \( n \), \( n-1 \)
• \( u^n_i \) and \( u^{n-1}_i \) are then already computed for \( i=0,\ldots,N_x \), and \( u^{n+1}_i \) is the unknown quantity

$$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right) \label{wave:pde1:step4} \end{equation} $$

The Courant number

$$ \begin{equation} C = c\frac{\Delta t}{\Delta x}, \end{equation} $$ is known as the (dimensionless) Courant number

The finite difference stencil

The stencil for the first time level

• Problem: the stencil for \( n=1 \) involves \( u^{-1}_i \), but time \( t=-\Delta t \) is outside the mesh
• Remedy: use the initial condition \( u_t=0 \) together with the stencil to eliminate \( u^{-1}_i \)

$$ [D_{2t}u=0]^0_i\quad\Rightarrow\quad u^{-1}_i=u^1_i$$

Insert in stencil \( [D_tD_tu = c^2D_xD_x]^0_i \) to get

$$ \begin{equation} u_i^1 = u^0_i - \half C^2\left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right) \label{wave:pde1:step4:1} \end{equation} $$

The algorithm

1. Compute \( u^0_i=I(x_i) \) for \( i=0,\ldots,N_x \)
2. Compute \( u^1_i \) by \eqref{wave:pde1:step4:1} and set \( u_i^1=0 \) for the boundary points \( i=0 \) and \( i=N_x \), for \( n=1,2,\ldots,N-1 \),
3. For each time level \( n=1,2,\ldots,N_t-1 \)

1. apply \eqref{wave:pde1:step4} to find \( u^{n+1}_i \) for \( i=1,\ldots,N_x-1 \)
2. set \( u^{n+1}_i=0 \) for the boundary points \( i=0 \), \( i=N_x \).

Moving finite difference stencil

web page or a movie file.

Sketch of an implementation (1)

• Arrays:

• u[i] stores \( u^{n+1}_i \)
• u_1[i] stores \( u^n_i \)
• u_2[i] stores \( u^{n-1}_i \)

PDE solvers should save memory

Sketch of an implementation (2)

# Given mesh points as arrays x and t (x[i], t[n])
dx = x[1] - x[0]
dt = t[1] - t[0]
C = c*dt/dx            # Courant number
Nt = len(t)-1
C2 = C**2              # Help variable in the scheme

# Set initial condition u(x,0) = I(x)
for i in range(0, Nx+1):
    u_1[i] = I(x[i])

# Apply special formula for first step, incorporating du/dt=0
for i in range(1, Nx):
    u[i] = u_1[i] - 0.5*C**2(u_1[i+1] - 2*u_1[i] + u_1[i-1])
u[0] = 0;  u[Nx] = 0   # Enforce boundary conditions

# Switch variables before next step
u_2[:], u_1[:] = u_1, u

for n in range(1, Nt):
    # Update all inner mesh points at time t[n+1]
    for i in range(1, Nx):
        u[i] = 2u_1[i] - u_2[i] - \ 
               C**2(u_1[i+1] - 2*u_1[i] + u_1[i-1])

    # Insert boundary conditions
    u[0] = 0;  u[Nx] = 0

    # Switch variables before next step
    u_2[:], u_1[:] = u_1, u

Verification

• Think about testing and verification before you start implementing the algorithm!
• Powerful testing tool: method of manufactured solutions and computation of convergence rates
• Will need a source term in the PDE and \( u_t(x,0)\neq 0 \)
• Even more powerful method: exact solution of the scheme

A slightly generalized model problem

Add source term \( f \) and nonzero initial condition \( u_t(x,0) \):

$$ \begin{align} u_{tt} &= c^2 u_{xx} + f(x,t), \label{wave:pde2}\\ u(x,0) &= I(x), \quad &x\in [0,L] \label{wave:pde2:ic:u}\\ u_t(x,0) &= V(x), \quad &x\in [0,L] \label{wave:pde2:ic:ut}\\ u(0,t) & = 0, \quad & t>0, \label{wave:pde2:bc:0}\\ u(L,t) & = 0, \quad &t>0 \label{wave:pde2:bc:L} \end{align} $$

Discrete model for the generalized model problem

$$ \begin{equation} [D_tD_t u = c^2 D_xD_x + f]^{n}_i \label{wave:pde2:fdop} \end{equation} $$

Writing out and solving for the unknown \( u^{n+1}_i \):

$$ \begin{equation} u^{n+1}_i = -u^{n-1}_i + 2u^n_i + C^2 (u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}) + \Delta t^2 f^n_i \label{wave:pde2:step3b} \end{equation} $$

Modified equation for the first time level

Centered difference for \( u_t(x,0) = V(x) \):

$$ [D_{2t}u = V]^0_i\quad\Rightarrow\quad u^{-1}_i = u^{1}_i - 2\Delta t V_i,$$

Inserting this in the stencil \eqref{wave:pde2:step3b} for \( n=0 \) leads to

$$ \begin{equation} u^{1}_i = u^0_i - \Delta t V_i + {\half} C^2 \left(u^{n}_{i+1}-2u^{n}_{i} + u^{n}_{i-1}\right) + \half\Delta t^2 f^n_i \label{wave:pde2:step3c} \end{equation} $$

Using an analytical solution of physical significance

• Standing waves occur in real life on a string
• Can be analyzed mathematically (known exact solution)

• PDE data: \( f=0 \), boundary conditions \( \uex(0,t)=\uex(L,0)=0 \), initial conditions \( I(x)=A\sin\left(\frac{\pi}{L}x\right) \) and \( V=0 \)
• Note: \( u_i^{n+1}\neq\uex(x_i,t_{n+1} \), and we do not know the error, so testing must aim at reproducing the expected convergence rates

Manufactured solution: principles

• Disadvantage with the previous physical solution: it does not test \( V\neq 0 \) and \( f\neq 0 \)
• Method of manufactured solution:

• Choose some \( \uex(x,t) \)
• Insert in PDE and fit \( f \)
• Set boundary and initial conditions compatible with the chosen \( \uex(x,t) \)

Manufactured solution: example

$$ \uex(x,t) = x(L-x)\sin t$$

PDE \( u_{tt}=c^2u_{xx}+f \):

$$ -x(L-x)\sin t = -2\sin t + f\quad\Rightarrow f = (2 - x(L-x))\sin t$$

Initial conditions become

$$ \begin{align*} u(x,0) &= I(x) = 0\\ u_t(x,0) &= V(x) = (2 - x(L-x))\cos t \end{align*} $$

Boundary conditions:

$$ u(x,0) = u(x,L) = 0 $$

Testing a manufactured solution

• Introduce common mesh parameter: \( h=\Delta t \), \( \Delta x =ch/C \)
• This \( h \) keeps \( C \) and \( \Delta t/\Delta x \) constant
• Select coarse mesh \( h \): \( h_0 \)
• Run experiments with \( h_i=2^{-i}h_0 \) (halving the cell size), \( i=0,\ldots,m \)
• Record the error \( E_i \) and \( h_i \) in each experiment
• Compute pariwise convergence rates \( r_i= \ln E_{i+1}/E_{i}/\ln h_{i+1}/h_{i} \)
• Verification: \( r_i\rightarrow 2 \) as \( i \) increases

Constructing an exact solution of the discrete equations

• Manufactured solution with computation of convergence rates: much manual work
• Simpler and more powerful: use an exact solution for \( u^{n}_i \)
• A linear or quadratic \( \uex \) in \( x \) and \( t \) is often a good candidate

Analytical work with the PDE problem

Here, choose \( \uex \) such that \( \uex(x,0)=\uex(L,0)=0 \):

$$ \uex (x,t) = x(L-x)(1+{\half}t), $$

Insert in the PDE and find \( f \):

$$ f(x,t)=2(1+t)c^2$$

Initial conditions:

$$ I(x) = x(L-x),\quad V(x)={\half}x(L-x) $$

Analytical work with the discrete equations (1)

We want to show that \( \uex \) also solves the discrete equations!

Useful preliminary result: $$ \begin{align} \lbrack D_tD_t t^2\rbrack^n &= \frac{t_{n+1}^2 - 2t_n^2 + t_{n-1}^2}{\Delta t^2} = (n+1)^2 -n^2 + (n-1)^2 = 2\\ \lbrack D_tD_t t\rbrack^n &= \frac{t_{n+1} - 2t_n + t_{n-1}}{\Delta t^2} = \frac{((n+1) -n + (n-1))\Delta t}{\Delta t^2} = 0 \end{align} $$

Hence, $$ [D_tD_t \uex]^n_i = x_i(L-x_i)[D_tD_t (1+{\half}t)]^n = x_i(L-x_i){\half}[D_tD_t t]^n = 0$$

Analytical work with the discrete equations (1)

$$ \begin{align*} \lbrack D_xD_x \uex\rbrack^n_i &= (1+{\half}t_n)\lbrack D_xD_x (xL-x^2)\rbrack_i = (1+{\half}t_n)\lbrack LD_xD_x x - D_xD_x x^2\rbrack_i \\ &= -2(1+{\half}t_n) \end{align*} $$

Now, \( f^n_i = 2(1+{\half}t_n)c^2 \) and we get

$$ [D_tD_t \uex - c^2D_xD_x\uex - f]^n_i = 0 - c^2(-1)2(1 + {\half}t_n + 2(1+{\half}t_n)c^2 = 0$$

Moreover, \( \uex(x_i,0)=I(x_i) \), \( \partial \uex/\partial t = V(x_i) \) at \( t=0 \), and \( \uex(x_0,t)=\uex(x_{N_x},0)=0 \). Also the modified scheme for the first time step is fulfilled by \( \uex(x_i,t_n) \).

Testing with the exact discrete solution

• We have established that \( u^{n+1}_i = \uex(x_i,t_{n+1})=x_i(L-x_i)(1+t_{n+1}/2) \)
• Run one simulation with one choice of \( c \), \( \Delta t \), and \( \Delta x \)
• Check that \( \max_i |u^{n+1}_i - \uex(x_i,t_{n+1})|<\epsilon \), \( \epsilon\sim 10^{-14} \) (machine precision + some round-off errors)
• This is the simplest and best verification test

Implementation

The algorithm

1. Compute \( u^0_i=I(x_i) \) for \( i=0,\ldots,N_x \)
2. Compute \( u^1_i \) by \eqref{wave:pde1:step4:1} and set \( u_i^1=0 \) for the boundary points \( i=0 \) and \( i=N_x \), for \( n=1,2,\ldots,N-1 \),
3. For each time level \( n=1,2,\ldots,N_t-1 \)

1. apply \eqref{wave:pde1:step4} to find \( u^{n+1}_i \) for \( i=1,\ldots,N_x-1 \)
2. set \( u^{n+1}_i=0 \) for the boundary points \( i=0 \), \( i=N_x \).

What do to with the solution?

• Different problem settings demand different actions with the computed \( u^{n+1}_i \) at each time step
• Solution: let the solver function make a callback to a user function where the user can do whatever is desired with the solution
• Advantage: solver just solves and user uses the solution

def user_action(u, x, t, n):
    # u[i] at spatial mesh points x[i] at time t[n]
    # plot u
    # or store u

Making a solver function

from numpy import *

def solver(I, V, f, c, L, Nx, C, T, user_action=None):
    """Solve u_tt=c^2*u_xx + f on (0,L)x(0,T]."""
    x = linspace(0, L, Nx+1)     # Mesh points in space
    dx = x[1] - x[0]
    dt = C*dx/c
    Nt = int(round(T/dt))
    t = linspace(0, Nt*dt, Nt+1) # Mesh points in time
    C2 = C**2                    # Help variable in the scheme
    if f is None or f == 0 :
        f = lambda x, t: 0
    if V is None or V == 0:
        V = lambda x: 0

    u   = zeros(Nx+1)   # Solution array at new time level
    u_1 = zeros(Nx+1)   # Solution at 1 time level back
    u_2 = zeros(Nx+1)   # Solution at 2 time levels back

    import time;  t0 = time.clock()  # for measuring CPU time

    # Load initial condition into u_1
    for i in range(0,Nx+1):
        u_1[i] = I(x[i])

    if user_action is not None:
        user_action(u_1, x, t, 0)

    # Special formula for first time step
    n = 0
    for i in range(1, Nx):
        u[i] = u_1[i] + dt*V(x[i]) + \ 
               0.5*C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1]) + \ 
               0.5*dt**2*f(x[i], t[n])
    u[0] = 0;  u[Nx] = 0

    if user_action is not None:
        user_action(u, x, t, 1)

    # Switch variables before next step
    u_2[:], u_1[:] = u_1, u

    for n in range(1, Nt):
        # Update all inner points at time t[n+1]
        for i in range(1, Nx):
            u[i] = - u_2[i] + 2*u_1[i] + \ 
                     C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1]) + \ 
                     dt**2*f(x[i], t[n])

        # Insert boundary conditions
        u[0] = 0;  u[Nx] = 0
        if user_action is not None:
            if user_action(u, x, t, n+1):
                break

        # Switch variables before next step
        u_2[:], u_1[:] = u_1, u

    cpu_time = t0 - time.clock()
    return u, x, t, cpu_time

Verification: exact quadratic solution

Exact solution of the PDE problem and the discrete equations: \( \uex (x,t) = x(L-x)(1+{\half}t) \)

import nose.tools as nt

def test_quadratic():
    """Check that u(x,t)=x(L-x)(1+t/2) is exactly reproduced."""
    def exact_solution(x, t):
        return x*(L-x)*(1 + 0.5*t)

    def I(x):
        return exact_solution(x, 0)

    def V(x):
        return 0.5*exact_solution(x, 0)

    def f(x, t):
        return 2*(1 + 0.5*t)*c**2

    L = 2.5
    c = 1.5
    Nx = 3  # Very coarse mesh
    C = 0.75
    T = 18

    u, x, t, cpu = solver(I, V, f, c, L, Nx, C, T)
    u_e = exact_solution(x, t[-1])
    diff = abs(u - u_e).max()
    nt.assert_almost_equal(diff, 0, places=14)

Visualization: animating \( u(x,t) \)

Make a viz function for animating the curve, with plotting in a user_action function plot_u:

def viz(I, V, f, c, L, Nx, C, T, umin, umax, animate=True):
    """Run solver and visualize u at each time level."""
    import scitools.std as plt
    import time, glob, os

    def plot_u(u, x, t, n):
        """user_action function for solver."""
        plt.plot(x, u, 'r-',
                 xlabel='x', ylabel='u',
                 axis=[0, L, umin, umax],
                 title='t=%f' % t[n], show=True)
        # Let the initial condition stay on the screen for 2
        # seconds, else insert a pause of 0.2 s between each plot
        time.sleep(2) if t[n] == 0 else time.sleep(0.2)
        plt.savefig('frame_%04d.png' % n)  # for movie making

    # Clean up old movie frames
    for filename in glob.glob('frame_*.png'):
        os.remove(filename)

    user_action = plot_u if animate else None
    u, x, t, cpu = solver(I, V, f, c, L, Nx, C, T, user_action)

    # Make movie files
    fps = 4  # Frames per second
    plt.movie('frame_*.png', encoder='html', fps=fps,
              output_file='movie.html')
    codec2ext = dict(flv='flv', libx64='mp4', libvpx='webm',
                     libtheora='ogg')
    filespec = 'frame_%04d.png'
    movie_program = 'avconv'  # or 'ffmpeg'
    for codec in codec2ext:
        ext = codec2ext[codec]
        cmd = '%(movie_program)s -r %(fps)d -i %(filespec)s '\ 
              '-vcodec %(codec)s movie.%(ext)s' % vars()
        os.system(cmd)

Note: plot_u is function inside function and remembers the local variables in viz (known as a closure).

Making movie files

• Store spatial curve in a file, for each time level
• Name files like 'something_%04d.png' % frame_counter
• Combine files to a movie

Terminal> scitools movie encoder=html output_file=movie.html \ 
          fps=4 frame_*.png  # web page with a player
Terminal> avconv -r 4 -i frame_%04d.png -vcodec flv       movie.flv
Terminal> avconv -r 4 -i frame_%04d.png -vcodec libtheora movie.ogg
Terminal> avconv -r 4 -i frame_%04d.png -vcodec libx264   movie.mp4
Terminal> avconv -r 4 -i frame_%04d.png -vcodec libtheora movie.ogg
Terminal> avconv -r 4 -i frame_%04d.png -vcodec libpvx    movie.webm

Running a case

• Vibrations of a guitar string
• Triangular initial shape (at rest)

Appropriate data:

• \( L=75 \) cm, \( x_0=0.8L \), \( a=5 \) mm, \( N_x=50 \), time frequency \( \nu = 440 \) Hz

Implementation of the case

def guitar(C):
    """Triangular wave (pulled guitar string)."""
    L = 0.75
    x0 = 0.8*L
    a = 0.005
    freq = 440
    wavelength = 2*L
    c = freq*wavelength
    omega = 2*pi*freq
    num_periods = 1
    T = 2*pi/omega*num_periods
    Nx = 50

    def I(x):
        return a*x/x0 if x < x0 else a/(L-x0)*(L-x)

    umin = -1.2*a;  umax = -umin
    cpu = viz(I, 0, 0, c, L, Nx, C, T, umin, umax, animate=True)

Program: wave1D_u0_s.py.

Resulting movie for \( C=0.8 \)

Movie of the vibrating string

The benefits of scaling

• It is difficult to figure out all the physical parameters of a case
• And it is not necessary because of a powerful: scaling

$$ \bar x = \frac{x}{L},\quad \bar t = \frac{c}{L}t,\quad \bar u = \frac{u}{a} $$

Insert this in the PDE (with \( f=0 \)) and dropping bars

$$ u_{tt} = u_{xx}$$

Initial condition: set \( a=1 \), \( L=1 \), and \( x_0\in [0,1] \) in \eqref{wave:pde1:guitar:I}.

In the code: set a=c=L=1, x0=0.8, and there is no need to calculate with wavelengths and frequencies to estimate \( c \)!

Just one challenge: determine the period of the waves and an appropriate end time (see the text for details).

Vectorization

• Problem: Python loops over long arrays are slow
• One remedy: use vectorized (numpy) code instead of explicit loops
• Other remedies: use Cython, port spatial loops to Fortran or C
• Speedup: 100-1000 (varies with \( N_x \))

Operations on slices of arrays

• Introductory example: compute \( d_i = u_{i+1}-u_i \)

n = u.size
for i in range(0, n-1):
    d[i] = u[i+1] - u[i]

• Note: all the differences here are independent of each other.
• Therefore \( d = (u_1,u_2,\ldots,u_n) - (u_0,u_1,\ldots,u_{n-1}) \)
• In numpy code: u[1:n] - u[0:n-1] or just u[1:] - u[:-1]

Test the understanding

Newcomers to vectorization are encouraged to choose a small array u, say with five elements, and simulate with pen and paper both the loop version and the vectorized version.

Vectorization of finite difference schemes (1)

Finite difference schemes basically contains differences between array elements with shifted indices. Consider the updating formula

for i in range(1, n-1):
    u2[i] = u[i-1] - 2*u[i] + u[i+1]

The vectorization consists of replacing the loop by arithmetics on slices of arrays of length n-2:

u2 = u[:-2] - 2*u[1:-1] + u[2:]
u2 = u[0:n-2] - 2*u[1:n-1] + u[2:n]   # alternative

Note: u2 gets length n-2.

If u2 is already an array of length n, do update on "inner" elements

u2[1:-1]  = u[:-2] - 2*u[1:-1] + u[2:]
u2[1:n-1] = u[0:n-2] - 2*u[1:n-1] + u[2:n]   # alternative

Vectorization of finite difference schemes (2)

Include a function evaluation too:

def f(x):
    return x**2 + 1

# Scalar version
for i in range(1, n-1):
    u2[i] = u[i-1] - 2*u[i] + u[i+1] + f(x[i])

# Vectorized version
u2[1:-1] = u[:-2] - 2*u[1:-1] + u[2:] + f(x[1:-1])

Vectorized implementation in the solver function

Scalar loop:

for i in range(1, Nx):
    u[i] = 2*u_1[i] - u_2[i] + \ 
           C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1])

Vectorized loop:

u[1:-1] = - u_2[1:-1] + 2*u_1[1:-1] + \ 
          C2*(u_1[:-2] - 2*u_1[1:-1] + u_1[2:])

or

u[1:Nx] = 2*u_1[1:Nx]- u_2[1:Nx] + \ 
          C2*(u_1[0:Nx-1] - 2*u_1[1:Nx] + u_1[2:Nx+1])

Program: wave1D_u0_sv.py

Verification of the vectorized version

def test_quadratic():
    """
    Check the scalar and vectorized versions work for
    a quadratic u(x,t)=x(L-x)(1+t/2) that is exactly reproduced.
    """
    # The following function must work for x as array or scalar
    exact_solution = lambda x, t: x*(L - x)*(1 + 0.5*t)
    I = lambda x: exact_solution(x, 0)
    V = lambda x: 0.5*exact_solution(x, 0)
    # f is a scalar (zeros_like(x) works for scalar x too)
    f = lambda x, t: zeros_like(x) + 2*c**2*(1 + 0.5*t)

    L = 2.5
    c = 1.5
    Nx = 3  # Very coarse mesh
    C = 1
    T = 18  # Long time integration

    def assert_no_error(u, x, t, n):
        u_e = exact_solution(x, t[n])
        diff = abs(u - u_e).max()
        nt.assert_almost_equal(diff, 0, places=13)

    solver(I, V, f, c, L, Nx, C, T,
           user_action=assert_no_error, version='scalar')
    solver(I, V, f, c, L, Nx, C, T,
           user_action=assert_no_error, version='vectorized')

Note:

• Compact code with lambda functions
• The scalar \( f \) value needs careful coding: return constant array if vectorized code, else number

Efficiency measurements

• Run wave1D_u0_sv.py for \( N_x \) as 50,100,200,400,800 and measuring the CPU time
• Observe substantial speed-up: vectorized version is about \( N_x/5 \) times faster

Generalization: reflecting boundaries

• Boundary condition \( u=0 \): \( u \) changes sign
• Boundary condition \( u_x=0 \): wave is perfectly reflected
• How can we implement \( u_x \)? (more complicated than \( u=0 \))

Demo of boundary conditions

Neumann boundary condition

$$ \begin{equation} \frac{\partial u}{\partial n} \equiv \normalvec\cdot\nabla u = 0 \label{wave:pde1:Neumann:0} \end{equation} $$

For a 1D domain \( [0,L] \):

$$ \left.\frac{\partial}{\partial n}\right\vert_{x=L} = \frac{\partial}{\partial x},\quad \left.\frac{\partial}{\partial n}\right\vert_{x=0} = - \frac{\partial}{\partial x} $$

Boundary condition terminology:

• \( u_x \) specified: Neumann condition
• \( u \) specified: Dirichlet condition

Discretization of derivatives at the boundary (1)

• How can we incorporate the condition \( u_x=0 \) in the finite difference scheme?
• We used centeral differences for \( u_{tt} \) and \( u_{xx} \): \( \Oof{\Delta t^2, \Delta x^2} \) accuracy
• Also for \( u_t(x,0) \)
• Should use central difference for \( u_x \) to preserve second order accuracy

Discretization of derivatives at the boundary (2)

$$ \frac{u_{-1}^n - u_1^n}{2\Delta x} = 0 $$

• Problem: \( u_{-1}^n \) is outside the mesh (fictitious value)
• Remedy: use the stencil at the boundary to eliminate \( u_{-1}^n \); just replace \( u_{-1}^n \) by \( u_{1}^n \)

Visualization of modified boundary stencil

Discrete equation for computing \( u^3_0 \) in terms of \( u^2_0 \), \( u^1_0 \), and \( u^2_1 \):

Animation in a web page or a movie file.

Implementation of Neumann conditions

• Use the general stencil for interior points also on the boundary
• Replace \( u_{i-1}^n \) by \( u_{i+1}^n \) for \( i=0 \)
• Replace \( u_{i+1}^n \) by \( u_{i-1}^n \) for \( i=N_x \)

i = 0
ip1 = i+1
im1 = ip1  # i-1 -> i+1
u[i] = u_1[i] + C2*(u_1[im1] - 2*u_1[i] + u_1[ip1])

i = Nx
im1 = i-1
ip1 = im1  # i+1 -> i-1
u[i] = u_1[i] + C2*(u_1[im1] - 2*u_1[i] + u_1[ip1])

# Or just one loop over all points

for i in range(0, Nx+1):
    ip1 = i+1 if i < Nx else i-1
    im1 = i-1 if i > 0  else i+1
    u[i] = u_1[i] + C2*(u_1[im1] - 2*u_1[i] + u_1[ip1])

Program wave1D_dn0.py

Moving finite difference stencil

web page or a movie file.

Index set notation

• Tedious to write index sets like \( i=0,\ldots,N_x \) and \( n=0,\ldots,N_t \)
• Notation not valid if \( i \) or \( n \) starts at 1 instead...
• Both in math and code it is advantageous to use index sets
• \( i\in\Ix \) instead of \( i=0,\ldots,N_x \)
• Definition: \( \Ix =\{0,\ldots,N_x\} \)
• The first index: \( i=\setb{\Ix} \)
• The last index: \( i=\sete{\Ix} \)
• All interior points: \( i\in\seti{\Ix} \), \( \seti{\Ix}=\{1,\ldots,N_x-1\} \)
• \( \setl{\Ix} \) means \( \{0,\ldots,N_x-1\} \)
• \( \setr{\Ix} \) means \( \{1,\ldots,N_x\} \)

Index set notation in code

Index sets in action (1)

Index sets for a problem in the \( x,t \) plane:

$$ \begin{equation} \Ix = \{0,\ldots,N_x\},\quad \It = \{0,\ldots,N_t\}, \end{equation} $$

Implemented in Python as

Ix = range(0, Nx+1)
It = range(0, Nt+1)

Index sets in action (2)

A finite difference scheme can with the index set notation be specified as

$$ \begin{align*} u^{n+1}_i &= -u^{n-1}_i + 2u^n_i + C^2 \left(u^{n}_{i+1}-2u^{n}_{i}+u^{n}_{i-1}\right), \quad i\in\seti{\Ix},\ n\in\seti{\It}\\ u_i &= 0, \quad i=\setb{\Ix},\ n\in\seti{\It}\\ u_i &= 0, \quad i=\sete{\Ix},\ n\in\seti{\It} \end{align*} $$

Corresponding implementation:

for n in It[1:-1]:
    for i in Ix[1:-1]:
        u[i] = - u_2[i] + 2*u_1[i] + \ 
               C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1])
    i = Ix[0];  u[i] = 0
    i = Ix[-1]; u[i] = 0

Program wave1D_dn.py

Alternative implementation via ghost cells

• Instead of modifying the stencil at the boundary, we extend the mesh to cover \( u_{-1}^n \) and \( u_{N_x+1}^n \)
• The extra left and right cell are called ghost cells
• The extra points are called ghost points
• The \( u_{-1}^n \) and \( u_{N_x+1}^n \) values are called ghost values
• Update ghost values as \( u_{i-1}^n = u_{i+1}^n \) for \( i=0 \) and \( i=N_x \)
• Then the stencil becomes right at the boundary

Implementation of ghost cells (1)

Add ghost points:

u   = zeros(Nx+3)
u_1 = zeros(Nx+3)
u_2 = zeros(Nx+3)

x = linspace(0, L, Nx+1)  # Mesh points without ghost points

• A major indexing problem arises with ghost cells since Python indices must start at 0.
• u[-1] will always mean the last element in u
• Math indexing: \( -1,0,1,2,\ldots,N_x+1 \)
• Python indexing: 0,..,Nx+2
• Remedy: use index sets

Implementation of ghost cells (2)

u = zeros(Nx+3)
Ix = range(1, u.shape[0]-1)

# Boundary values: u[Ix[0]], u[Ix[-1]]

# Set initial conditions
for i in Ix:
    u_1[i] = I(x[i-Ix[0]])  # Note i-Ix[0]

# Loop over all physical mesh points
for i in Ix:
    u[i] = - u_2[i] + 2*u_1[i] + \ 
           C2*(u_1[i-1] - 2*u_1[i] + u_1[i+1])

# Update ghost values
i = Ix[0]          # x=0 boundary
u[i-1] = u[i+1]
i = Ix[-1]         # x=L boundary
u[i-1] = u[i+1]

Program: wave1D_dn0_ghost.py.

Generalization: variable wave velocity

Heterogeneous media: varying \( c=c(x) \)

The model PDE with a variable coefficient

$$ \begin{equation} \frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) + f(x,t) \label{wave:pde2:var:c:pde} \end{equation} $$

This equation sampled at a mesh point \( (x_i,t_n) \): $$ \frac{\partial^2 }{\partial t^2} u(x_i,t_n) = \frac{\partial}{\partial x}\left( q(x_i) \frac{\partial}{\partial x} u(x_i,t_n)\right) + f(x_i,t_n), $$

Discretizing the variable coefficient (1)

The principal idea is to first discretize the outer derivative.

Define $$ \phi = q(x) \frac{\partial u}{\partial x} $$

Then use a centered derivative around \( x=x_i \) for the derivative of \( \phi \):

$$ \left[\frac{\partial\phi}{\partial x}\right]^n_i \approx \frac{\phi_{i+\half} - \phi_{i-\half}}{\Delta x} = [D_x\phi]^n_i $$

Discretizing the variable coefficient (2)

Then discretize the inner operators: $$ \phi_{i+\half} = q_{i+\half} \left[\frac{\partial u}{\partial x}\right]^n_{i+\half} \approx q_{i+\half} \frac{u^n_{i+1} - u^n_{i}}{\Delta x} = [q D_x u]_{i+\half}^n $$

Similarly, $$ \phi_{i-\half} = q_{i-\half} \left[\frac{\partial u}{\partial x}\right]^n_{i-\half} \approx q_{i-\half} \frac{u^n_{i} - u^n_{i-1}}{\Delta x} = [q D_x u]_{i-\half}^n $$

Discretizing the variable coefficient (3)

These intermediate results are now combined to

$$ \begin{equation} \left[ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right)\right]^n_i \approx \frac{1}{\Delta x^2} \left( q_{i+\half} \left({u^n_{i+1} - u^n_{i}}\right) - q_{i-\half} \left({u^n_{i} - u^n_{i-1}}\right)\right) \label{wave:pde2:var:c:formula} \end{equation} $$

In operator notation: $$ \begin{equation} \left[ \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right)\right]^n_i \approx [D_xq D_x u]^n_i \label{wave:pde2:var:c:formula:op} \end{equation} $$

Computing the coefficient between mesh points

• Given \( q(x) \): compute \( q_{i+\half} \) as \( q(x_{i+\half}) \)
• Given \( q \) at the mesh points: \( q_i \), use an average

The arithmetic mean in \eqref{wave:pde2:var:c:mean:arithmetic} is by far the most used averaging technique.

Discretization of variable-coefficient wave equation in operator notation

$$ \begin{equation} \lbrack D_tD_t u = D_x\overline{q}^{x}D_x u + f\rbrack^{n}_i \label{wave:pde2:var:c:scheme:op} \end{equation} $$

We clearly see the type of finite differences and averaging!

Write out and solve wrt \( u_i^{n+1} \):

$$ \begin{align} u^{n+1}_i &= - u_i^{n-1} + 2u_i^n + \left(\frac{\Delta x}{\Delta t}\right)^2\times \nonumber\\ &\quad \left( \half(q_{i} + q_{i+1})(u_{i+1}^n - u_{i}^n) - \half(q_{i} + q_{i-1})(u_{i}^n - u_{i-1}^n)\right) + \nonumber\\ & \quad \Delta t^2 f^n_i \label{wave:pde2:var:c:scheme:impl} \end{align} $$

Neumann condition and a variable coefficient

Consider \( \partial u/\partial x=0 \) at \( x=L=N_x\Delta x \):

$$ \frac{u_{i+1}^{n} - u_{i-1}^n}{2\Delta x} = 0\quad u_{i+1}^n = u_{i-1}^n, \quad i=N_x $$

Insert \( u_{i+1}^n=u_{i-1}^n \) in the stencil \eqref{wave:pde2:var:c:scheme:impl} for \( i=N_x \) and obtain

$$ u^{n+1}_i \approx - u_i^{n-1} + 2u_i^n + \left(\frac{\Delta x}{\Delta t}\right)^2 2q_{i}(u_{i-1}^n - u_{i}^n) + \Delta t^2 f^n_i $$

(We have used \( q_{i+\half} + q_{i-\half}\approx 2q_i \).)

Alternative: assume \( dq/dx=0 \) (simpler).

Implementation of variable coefficients

Assume c[i] holds \( c_i \) the spatial mesh points

for i in range(1, Nx):
    u[i] = - u_2[i] + 2*u_1[i] + \ 
           C2*(0.5*(q[i] + q[i+1])*(u_1[i+1] - u_1[i])  - \ 
               0.5*(q[i] + q[i-1])*(u_1[i] - u_1[i-1])) + \ 
           dt2*f(x[i], t[n])

Here: C2=(dt/dx)**2

Vectorized version:

u[1:-1] = - u_2[1:-1] + 2*u_1[1:-1] + \ 
          C2*(0.5*(q[1:-1] + q[2:])*(u_1[2:] - u_1[1:-1]) -
              0.5*(q[1:-1] + q[:-2])*(u_1[1:-1] - u_1[:-2])) + \ 
          dt2*f(x[1:-1], t[n])

Neumann condition \( u_x=0 \): same ideas as in 1D (modified stencil or ghost cells).

A more general model PDE with variable coefficients

$$ \begin{equation} \varrho(x)\frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( q(x) \frac{\partial u}{\partial x}\right) + f(x,t) \label{wave:pde2:var:c:pde2} \end{equation} $$

A natural scheme is

$$ \begin{equation} [\varrho D_tD_t u = D_x\overline{q}^xD_x u + f]^n_i \end{equation} $$

Or

$$ \begin{equation} [D_tD_t u = \varrho^{-1}D_x\overline{q}^xD_x u + f]^n_i \end{equation} $$

No need to average \( \varrho \), just sample at \( i \)

Generalization: damping

Why do waves die out?

• Damping (non-elastic effects, air resistance)
• 2D/3D: conservation of energy makes an amplitude reduction by \( 1/\sqrt{r} \) (2D) or \( 1/r \) (3D)

$$ \begin{equation} \frac{\partial^2 u}{\partial t^2} + \color{red}{b\frac{\partial u}{\partial t}} = c^2\frac{\partial^2 u}{\partial x^2} + f(x,t), \label{wave:pde3} \end{equation} $$

\( b \geq 0 \): prescribed damping coefficient.

Discretization via centered differences to ensure \( \Oof{\Delta t^2} \) error:

$$ \begin{equation} [D_tD_t u + bD_{2t}u = c^2D_xD_x u + f]^n_i \label{wave:pde3:fd} \end{equation} $$

Need special formula for \( u^1_i \) + special stencil (or ghost cells) for Neumann conditions.

Building a general 1D wave equation solver

The program wave1D_dn_vc.py solves a fairly general 1D wave equation:

$$ \begin{align} u_t &= (c^2(x)u_x)_x + f(x,t),\quad &x\in (0,L),\ t\in (0,T] \label{wave:pde2:software:ueq}\\ u(x,0) &= I(x),\quad &x\in [0,L] \label{wave:pde2:software:u0}\\ u_t(x,0) &= V(t),\quad &x\in [0,L] \label{wave:pde2:software:ut0}\\ u(0,t) &= U_0(t)\hbox{ or } u_x(0,t)=0,\quad &t\in (0,T] \label{wave:pde2:software:bc0}\\ u(L,t) &= U_L(t)\hbox{ or } u_x(L,t)=0,\quad &t\in (0,T] \label{wave:pde2:software:bcL} \end{align} $$

Can be adapted to many needs.

Collection of initial conditions

The function pulse in wave1D_dn_vc.py offers four initial conditions:

1. a rectangular pulse ("plug")
2. a Gaussian function (gaussian)
3. a "cosine hat": one period of \( 1 + \cos (\pi x \), \( x\in [-1,1] \)
4. half a "cosine hat": half a period of \( \cos \pi x \), \( x\in [-{\half},{\half}] \)

>>> import wave1D_dn_vc as w
>>> w.pulse(loc='left', pulse_tp='cosinehat', Nx=50, every_frame=10)

Finite difference methods for 2D and 3D wave equations

Constant wave velocity \( c \):

$$ \begin{equation} \frac{\partial^2 u}{\partial t^2} = c^2\nabla^2 u\hbox{ for }\xpoint\in\Omega\subset\Real^d,\ t\in (0,T] \label{wave:2D3D:model1} \end{equation} $$

Variable wave velocity:

$$ \begin{equation} \varrho\frac{\partial^2 u}{\partial t^2} = \nabla\cdot (q\nabla u) + f\hbox{ for }\xpoint\in\Omega\subset\Real^d,\ t\in (0,T] \label{wave:2D3D:model2} \end{equation} $$

Examples on wave equations written out in 2D/3D

3D, constant \( c \):

$$ \begin{equation*} \nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \end{equation*} $$

2D, variable \( c \):

$$ \begin{equation} \varrho(x,y) \frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( q(x,y) \frac{\partial u}{\partial x}\right) + \frac{\partial}{\partial y}\left( q(x,y) \frac{\partial u}{\partial y}\right) + f(x,y,t) \end{equation} $$

Compact notation:

$$ \begin{align} u_{tt} &= c^2(u_{xx} + u_{yy} + u_{zz}) + f, \label{wave:2D3D:model1:v2}\\ \varrho u_{tt} &= (q u_x)_x + (q u_z)_z + (q u_z)_z + f \label{wave:2D3D:model2:v2} \end{align} $$

Boundary and initial conditions

We need one boundary condition at each point on \( \partial\Omega \):

1. \( u \) is prescribed (\( u=0 \) or known incoming wave)
2. \( \partial u/\partial n = \normalvec\cdot\nabla u \) prescribed (\( =0 \): reflecting boundary)
3. open boundary (radiation) condition: \( u_t + \boldsymbol{c}\cdot\nabla u =0 \) (let waves travel undisturbed out of the domain)

1. \( u=I \),
2. \( u_t = V \).

Example: 2D propagation of Gaussian function

Mesh

• Mesh point: \( (x_i,y_j,z_k,t_n) \)
• \( x \) direction: \( x_0 < x_1 <\cdots < x_{N_x} \)
• \( y \) direction: \( y_0 < y_1 <\cdots < y_{N_y} \)
• \( z \) direction: \( z_0 < z_1 <\cdots < z_{N_z} \)
• \( u^{n}_{i,j,k} \approx \uex(x_i,y_j,z_k,t_n) \)

Discretization

$$ [D_tD_t u = c^2(D_xD_x u + D_yD_yu) + f]^n_{i,j,k}, $$ Written out in detail:

$$ \begin{align*} \frac{u^{n+1}_{i,j} - 2u^{n}_{i,j} + u^{n-1}_{i,j}}{\Delta t^2} &= c^2 \frac{u^{n}_{i+1,j} - 2u^{n}_{i,j} + u^{n}_{i-1,j}}{\Delta x^2} + \nonumber\\ &\quad c^2\frac{u^{n}_{i,j+1} - 2u^{n}_{i,j} + u^{n}_{i,j-1}}{\Delta y^2} + f^n_{i,j}, \end{align*} $$

\( u^{n-1}_{i,j} \) and \( u^n_{i,j} \) are known, solve for \( u^{n+1}_{i,j} \):

$$ u^{n+1}_{i,j} = 2u^n_{i,j} + u^{n-1}_{i,j} + c^2\Delta t^2[D_xD_x u + D_yD_y u]^n_{i,j}$$

Special stencil for the first time step

• The stencil for \( u^1_{i,j} \) (\( n=0 \)) involves \( u^{-1}_{i,j} \) which is outside the time mesh
• Remedy: use discretized \( u_t(x,0)=V \) and the stencil for \( n=0 \) to develop a special stencil (as in the 1D case)

$$ u^{n+1}_{i,j} = u^n_{i,j} -2\Delta V_{i,j} + {\half} c^2\Delta t^2[D_xD_x u + D_yD_y u]^n_{i,j}$$

Variable coefficients (1)

3D wave equation:

$$ \varrho u_{tt} = (qu_x)_x + (qu_y)_y + (qu_z)_z + f(x,y,z,t) $$

Just apply the 1D discretization for each term:

$$ \begin{equation} [\varrho D_tD_t u = (D_x\overline{q}^x D_x u + D_y\overline{q}^y D_yu + D_z\overline{q}^z D_z u) + f]^n_{i,j,k} \end{equation} $$

Need special formula for \( u^1_{i,j,k} \) (use \( [D_{2t}u=V]^0 \) and stencil for \( n=0 \)).

Variable coefficients (2)

Written out:

$$ \begin{align*} u^{n+1}_{i,j,k} &= - u^{n-1}_{i,j,k} + 2u^{n}_{i,j,k} + \\ &= \frac{1}{\varrho_{i,j,k}}\frac{1}{\Delta x^2} ( \half(q_{i,j,k} + q_{i+1,j,k})(u^{n}_{i+1,j,k} - u^{n}_{i,j,k}) - \\ &\qquad\quad \half(q_{i-1,j,k} + q_{i,j,k})(u^{n}_{i,j,k} - u^{n}_{i-1,j,k})) + \\ &= \frac{1}{\varrho_{i,j,k}}\frac{1}{\Delta x^2} ( \half(q_{i,j,k} + q_{i,j+1,k})(u^{n}_{i,j+1,k} - u^{n}_{i,j,k}) - \\ &\qquad\quad\half(q_{i,j-1,k} + q_{i,j,k})(u^{n}_{i,j,k} - u^{n}_{i,j-1,k})) + \\ &= \frac{1}{\varrho_{i,j,k}}\frac{1}{\Delta x^2} ( \half(q_{i,j,k} + q_{i,j,k+1})(u^{n}_{i,j,k+1} - u^{n}_{i,j,k}) -\\ &\qquad\quad \half(q_{i,j,k-1} + q_{i,j,k})(u^{n}_{i,j,k} - u^{n}_{i,j,k-1})) + \\ + &\qquad \Delta t^2 f^n_{i,j,k} \end{align*} $$

Neumann boundary condition in 2D

Use ideas from 1D! Example: \( \frac{\partial u}{\partial n} \) at \( y=0 \), \( \frac{\partial u}{\partial n} = -\frac{\partial u}{\partial y} \)

Boundary condition discretization:

$$ [-D_{2y} u = 0]^n_{i,0}\quad\Rightarrow\quad \frac{u^n_{i,1}-u^n_{i,-1}}{2\Delta y} = 0,\ i\in\Ix $$

Insert \( u^n_{i,-1}=u^n_{i,1} \) in the stencil for \( u^{n+1}_{i,j=0} \) to obtain a modified stencil on the boundary.

Pattern: use interior stencil also on the bundary, but replace \( j-1 \) by \( j+1 \)

Alternative: use ghost cells and ghost values

Implementation of 2D/3D problems

$$ \begin{align} u_t &= c^2(u_{xx} + u_{yy}) + f(x,y,t),\quad &(x,y)\in \Omega,\ t\in (0,T]\\ u(x,y,0) &= I(x,y),\quad &(x,y)\in\Omega\\ u_t(x,y,0) &= V(x,y),\quad &(x,y)\in\Omega\\ u &= 0,\quad &(x,y)\in\partial\Omega,\ t\in (0,T] \end{align} $$

\( \Omega = [0,L_x]\times [0,L_y] \)

Discretization:

$$ [D_t D_t u = c^2(D_xD_x u + D_yD_y u) + f]^n_{i,j}, $$

Algorithm

1. Set initial condition \( u^0_{i,j}=I(x_i,y_j) \)
2. Compute \( u^1_{i,j} = \cdots \) for \( i\in\seti{\Ix} \) and \( j\in\seti{\Iy} \)
3. Set \( u^1_{i,j}=0 \) for the boundaries \( i=0,N_x \), \( j=0,N_y \)
4. For \( n=1,2,\ldots,N_t \):

1. Find \( u^{n+1}_{i,j} = \cdots \) for \( i\in\seti{\Ix} \) and \( j\in\seti{\Iy} \)
2. Set \( u^{n+1}_{i,j}=0 \) for the boundaries \( i=0,N_x \), \( j=0,N_y \)

Scalar computations: mesh

Program: wave2D_u0.py

def solver(I, V, f, c, Lx, Ly, Nx, Ny, dt, T,
           user_action=None, version='scalar'):

Mesh:

x = linspace(0, Lx, Nx+1)                  # mesh points in x dir
y = linspace(0, Ly, Ny+1)                  # mesh points in y dir
dx = x[1] - x[0]
dy = y[1] - y[0]
Nt = int(round(T/float(dt)))
t = linspace(0, N*dt, N+1)                 # mesh points in time
Cx2 = (c*dt/dx)**2;  Cy2 = (c*dt/dy)**2    # help variables
dt2 = dt**2

Scalar computations: arrays

Store \( u^{n+1}_{i,j} \), \( u^{n}_{i,j} \), and \( u^{n-1}_{i,j} \) in three two-dimensional arrays:

u   = zeros((Nx+1,Ny+1))   # solution array
u_1 = zeros((Nx+1,Ny+1))   # solution at t-dt
u_2 = zeros((Nx+1,Ny+1))   # solution at t-2*dt

\( u^{n+1}_{i,j} \) corresponds to u[i,j], etc.

Scalar computations: initial condition

Ix = range(0, u.shape[0])
Iy = range(0, u.shape[1])
It = range(0, t.shape[0])

for i in Ix:
    for j in Iy:
        u_1[i,j] = I(x[i], y[j])

if user_action is not None:
    user_action(u_1, x, xv, y, yv, t, 0)

Arguments xv and yv: for vectorized computations

Scalar computations: primary stencil

def advance_scalar(u, u_1, u_2, f, x, y, t, n, Cx2, Cy2, dt,
                   V=None, step1=False):
    Ix = range(0, u.shape[0]);  Iy = range(0, u.shape[1])
    dt2 = dt**2
    if step1:
        Cx2 = 0.5*Cx2;  Cy2 = 0.5*Cy2; dt2 = 0.5*dt2
        D1 = 1;  D2 = 0
    else:
        D1 = 2;  D2 = 1
    for i in Ix[1:-1]:
        for j in Iy[1:-1]:
            u_xx = u_1[i-1,j] - 2*u_1[i,j] + u_1[i+1,j]
            u_yy = u_1[i,j-1] - 2*u_1[i,j] + u_1[i,j+1]
            u[i,j] = D1*u_1[i,j] - D2*u_2[i,j] + \ 
                     Cx2*u_xx + Cy2*u_yy + dt2*f(x[i], y[j], t[n])
            if step1:
                u[i,j] += dt*V(x[i], y[j])
    # Boundary condition u=0
    j = Iy[0]
    for i in Ix: u[i,j] = 0
    j = Iy[-1]
    for i in Ix: u[i,j] = 0
    i = Ix[0]
    for j in Iy: u[i,j] = 0
    i = Ix[-1]
    for j in Iy: u[i,j] = 0
    return u

D1 and D2: allow advance_scalar to be used also for \( u^1_{i,j} \):

u = advance_scalar(u, u_1, u_2, f, x, y, t,
                   n, 0.5*Cx2, 0.5*Cy2, 0.5*dt2, D1=1, D2=0)

Vectorized computations: mesh coordinates

Mesh with \( 30\times 30 \) cells: vectorization reduces the CPU time by a factor of 70 (!).

Need special coordinate arrays xv and yv such that \( I(x,y) \) and \( f(x,y,t) \) can be vectorized:

from numpy import newaxis
xv = x[:,newaxis]
yv = y[newaxis,:]

u_1[:,:] = I(xv, yv)
f_a[:,:] = f(xv, yv, t)

Vectorized computations: stencil

def advance_vectorized(u, u_1, u_2, f_a, Cx2, Cy2, dt,
                       V=None, step1=False):
    dt2 = dt**2
    if step1:
        Cx2 = 0.5*Cx2;  Cy2 = 0.5*Cy2; dt2 = 0.5*dt2
        D1 = 1;  D2 = 0
    else:
        D1 = 2;  D2 = 1
    u_xx = u_1[:-2,1:-1] - 2*u_1[1:-1,1:-1] + u_1[2:,1:-1]
    u_yy = u_1[1:-1,:-2] - 2*u_1[1:-1,1:-1] + u_1[1:-1,2:]
    u[1:-1,1:-1] = D1*u_1[1:-1,1:-1] - D2*u_2[1:-1,1:-1] + \ 
                   Cx2*u_xx + Cy2*u_yy + dt2*f_a[1:-1,1:-1]
    if step1:
        u[1:-1,1:-1] += dt*V[1:-1, 1:-1]
    # Boundary condition u=0
    j = 0
    u[:,j] = 0
    j = u.shape[1]-1
    u[:,j] = 0
    i = 0
    u[i,:] = 0
    i = u.shape[0]-1
    u[i,:] = 0
    return u

Verification: quadratic solution (1)

Manufactured solution:

$$ \begin{equation} \uex(x,y,t) = x(L_x-x)y(L_y-y)(1+{\half}t) \label{wave2D3D:impl:verify:quadratic} \end{equation} $$

Requires \( f=2c^2(1+{\half}t)(y(L_y-y) + x(L_x-x)) \).

This \( \uex \) is ideal because it also solves the discrete equations!

Verification: quadratic solution (2)

• \( [D_t D_t 1]^n=0 \)
• \( [D_t D_t t]^n=0 \)
• \( [D_t D_t t^2]=2 \)
• \( D_tD_t \) is a linear operator: \( [D_tD_t (au+bv)]^n = a[D_tD_t u]^n + b[D_tD_t v]^n \)

• Similar calculations for \( [D_yD_y\uex]^n_{i,j} \) and \( [D_tD_t \uex]^n_{i,j} \) terms
• Must also check the equation for \( u^1_{i,j} \)

Migrating loops to Cython

• Vectorization: 5-10 times slower than pure C or Fortran code
• Cython: extension of Python for translating functions to C
• Principle: declare variables with type

Declaring variables and annotating the code

Pure Python code:

def advance_scalar(u, u_1, u_2, f, x, y, t,
                   n, Cx2, Cy2, dt2, D1=2, D2=1):
    Ix = range(0, u.shape[0]);  Iy = range(0, u.shape[1])
    for i in Ix[1:-1]:
        for j in Iy[1:-1]:
            u_xx = u_1[i-1,j] - 2*u_1[i,j] + u_1[i+1,j]
            u_yy = u_1[i,j-1] - 2*u_1[i,j] + u_1[i,j+1]
            u[i,j] = D1*u_1[i,j] - D2*u_2[i,j] + \ 
                     Cx2*u_xx + Cy2*u_yy + dt2*f(x[i], y[j], t[n])

• Copy this function and put it in a file with .pyx extension.
• Add type of variables:

• function(a, b) \( \rightarrow \) cpdef function(int a, double b)
• v = 1.2 \( \rightarrow \) cdef double v = 1.2
• Array declaration: np.ndarray[np.float64_t, ndim=2, mode='c'] u

Cython version of the functions

import numpy as np
cimport numpy as np
cimport cython
ctypedef np.float64_t DT    # data type

@cython.boundscheck(False)  # turn off array bounds check
@cython.wraparound(False)   # turn off negative indices (u[-1,-1])
cpdef advance(
    np.ndarray[DT, ndim=2, mode='c'] u,
    np.ndarray[DT, ndim=2, mode='c'] u_1,
    np.ndarray[DT, ndim=2, mode='c'] u_2,
    np.ndarray[DT, ndim=2, mode='c'] f,
    double Cx2, double Cy2, double dt2):

    cdef int Nx, Ny, i, j
    cdef double u_xx, u_yy
    Nx = u.shape[0]-1
    Ny = u.shape[1]-1
    for i in xrange(1, Nx):
        for j in xrange(1, Ny):
            u_xx = u_1[i-1,j] - 2*u_1[i,j] + u_1[i+1,j]
            u_yy = u_1[i,j-1] - 2*u_1[i,j] + u_1[i,j+1]
            u[i,j] = 2*u_1[i,j] - u_2[i,j] + \ 
                     Cx2*u_xx + Cy2*u_yy + dt2*f[i,j]

Note: from now in we skip the code for setting boundary values

Visual inspection of the C translation

See how effective Cython can translate this code to C:

Terminal> cython -a wave2D_u0_loop_cy.pyx

Load wave2D_u0_loop_cy.html in a browser (white: pure C, yellow: still Python):

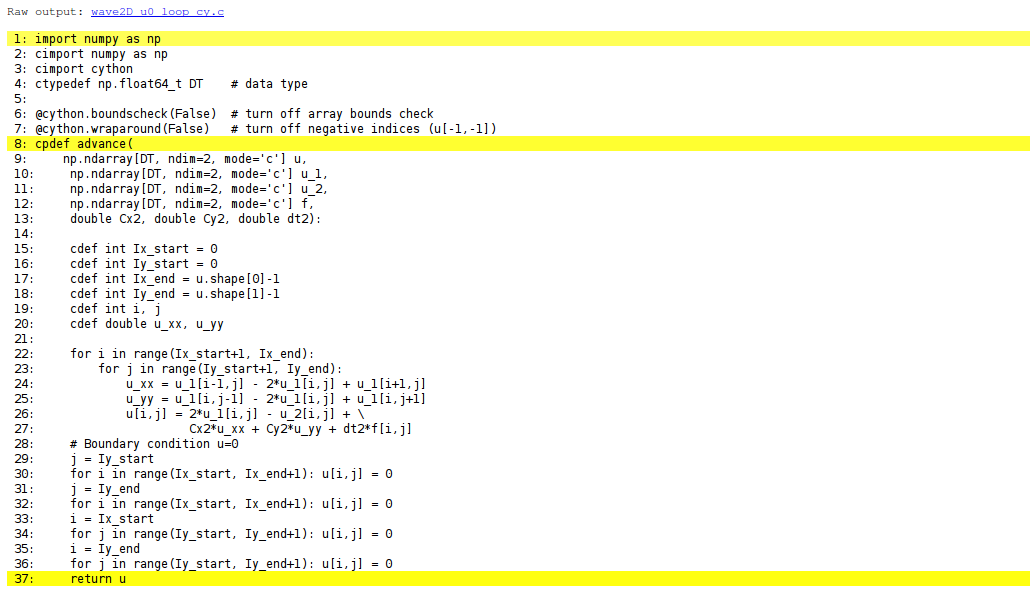
Can click on wave2D_u0_loop_cy.c to see the generated C code...

Building the extension module

• Cython code must be translated to C
• C code must be compiled
• Compiled C code must be linked to Python C libraries
• Result: C extension module (.so file) that can be loaded as a standard Python module
• Use a setup.py script to build the extension module

from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext

cymodule = 'wave2D_u0_loop_cy'
setup(
  name=cymodule
  ext_modules=[Extension(cymodule, [cymodule + '.pyx'],)],
  cmdclass={'build_ext': build_ext},
)

Terminal> python setup.py build_ext --inplace

Calling the Cython function from Python

import wave2D_u0_loop_cy
advance = wave2D_u0_loop_cy.advance
...
for n in It[1:-1:                  # time loop
    f_a[:,:] = f(xv, yv, t[n])     # precompute, size as u
    u = advance(u, u_1, u_2, f_a, x, y, t, Cx2, Cy2, dt2)

Efficiency:

• \( 120\times 120 \) cells in space:

• Pure Python: 1370 CPU time units
• Vectorized numpy: 5.5
• Cython: 1
• \( 60\times 60 \) cells in space:

• Pure Python: 1000 CPU time units
• Vectorized numpy: 6
• Cython: 1

Migrating loops to Fortran

• Write the advance function in pure Fortran
• Use f2py to generate C code for calling Fortran from Python
• Full manual control of the translation to Fortran

The Fortran subroutine

      subroutine advance(u, u_1, u_2, f, Cx2, Cy2, dt2, Nx, Ny)
      integer Nx, Ny
      real*8 u(0:Nx,0:Ny), u_1(0:Nx,0:Ny), u_2(0:Nx,0:Ny)
      real*8 f(0:Nx, 0:Ny), Cx2, Cy2, dt2
      integer i, j
Cf2py intent(in, out) u

C     Scheme at interior points
      do j = 1, Ny-1
         do i = 1, Nx-1
            u(i,j) = 2*u_1(i,j) - u_2(i,j) +
     &      Cx2*(u_1(i-1,j) - 2*u_1(i,j) + u_1(i+1,j)) +
     &      Cy2*(u_1(i,j-1) - 2*u_1(i,j) + u_1(i,j+1)) +
     &      dt2*f(i,j)
         end do
      end do

Note: Cf2py comment declares u as input argument and return value back to Python

Building the Fortran module with f2py

Terminal> f2py -m wave2D_u0_loop_f77 -h wave2D_u0_loop_f77.pyf \ 
          --overwrite-signature wave2D_u0_loop_f77.f
Terminal> f2py -c wave2D_u0_loop_f77.pyf --build-dir build_f77 \ 
          -DF2PY_REPORT_ON_ARRAY_COPY=1 wave2D_u0_loop_f77.f

f2py changes the argument list (!)

>>> import wave2D_u0_loop_f77
>>> print wave2D_u0_loop_f77.__doc__
This module 'wave2D_u0_loop_f77' is auto-generated with f2py....
Functions:
  u = advance(u,u_1,u_2,f,cx2,cy2,dt2,
      nx=(shape(u,0)-1),ny=(shape(u,1)-1))

• Array limits have default values
• Examine doc strings from f2py!

How to avoid array copying

• Two-dimensional arrays are stored row by row in Python and C
• Two-dimensional arrays are stored column by column in Fortran
• f2py takes a copy of a numpy (C) array and transposes it when calling Fortran
• Such copies are time and memory consuming
• Remedy: declare numpy arrays with Fortran storage

order = 'Fortran' if version == 'f77' else 'C'
u   = zeros((Nx+1,Ny+1), order=order)
u_1 = zeros((Nx+1,Ny+1), order=order)
u_2 = zeros((Nx+1,Ny+1), order=order)

Option -DF2PY_REPORT_ON_ARRAY_COPY=1 makes f2py write out array copying:

Terminal> f2py -c wave2D_u0_loop_f77.pyf --build-dir build_f77 \ 
          -DF2PY_REPORT_ON_ARRAY_COPY=1 wave2D_u0_loop_f77.f

Efficiency of translating to Fortran

• Same efficiency (in this example) as Cython and C
• About 5 times faster than vectorized numpy code
• \( >1000 \) faster than pure Python code

Migrating loops to C via Cython

• Write the advance function in pure C
• Use Cython to generate C code for calling C from Python
• Full manual control of the translation to C

The C code

• numpy arrays transferred to C are one-dimensional in C
• Need to translate [i,j] indices to single indices

/* Translate (i,j) index to single array index */
#define idx(i,j) (i)*(Ny+1) + j

void advance(double* u, double* u_1, double* u_2, double* f,
	     double Cx2, double Cy2, double dt2,
	     int Nx, int Ny)
{
  int i, j;
  /* Scheme at interior points */
  for (i=1; i<=Nx-1; i++) {
    for (j=1; j<=Ny-1; j++) {
        u[idx(i,j)] = 2*u_1[idx(i,j)] - u_2[idx(i,j)] +
        Cx2*(u_1[idx(i-1,j)] - 2*u_1[idx(i,j)] + u_1[idx(i+1,j)]) +
        Cy2*(u_1[idx(i,j-1)] - 2*u_1[idx(i,j)] + u_1[idx(i,j+1)]) +
        dt2*f[idx(i,j)];
	}
    }
  }
}

The Cython interface file

import numpy as np
cimport numpy as np
cimport cython

cdef extern from "wave2D_u0_loop_c.h":
    void advance(double* u, double* u_1, double* u_2, double* f,
                 double Cx2, double Cy2, double dt2,
                 int Nx, int Ny)

@cython.boundscheck(False)
@cython.wraparound(False)
def advance_cwrap(
    np.ndarray[double, ndim=2, mode='c'] u,
    np.ndarray[double, ndim=2, mode='c'] u_1,
    np.ndarray[double, ndim=2, mode='c'] u_2,
    np.ndarray[double, ndim=2, mode='c'] f,
    double Cx2, double Cy2, double dt2):
    advance(&u[0,0], &u_1[0,0], &u_2[0,0], &f[0,0],
            Cx2, Cy2, dt2,
            u.shape[0]-1, u.shape[1]-1)
    return u

Building the extension module

Compile and link the extension module with a setup.py file:

from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext

sources = ['wave2D_u0_loop_c.c', 'wave2D_u0_loop_c_cy.pyx']
module = 'wave2D_u0_loop_c_cy'
setup(
  name=module,
  ext_modules=[Extension(module, sources,
                         libraries=[], # C libs to link with
                         )],
  cmdclass={'build_ext': build_ext},
)

Terminal> python setup.py build_ext --inplace

In Python:

import wave2D_u0_loop_c_cy
advance = wave2D_u0_loop_c_cy.advance_cwrap
...
f_a[:,:] = f(xv, yv, t[n])
u = advance(u, u_1, u_2, f_a, Cx2, Cy2, dt2)

Migrating loops to C via f2py

• Write the advance function in pure C
• Use f2py to generate C code for calling C from Python
• Full manual control of the translation to C

The C code and the Fortran interface file

• Write the C function advance as before
• Write a Fortran 90 module defining the signature of the advance function
• Or: write a Fortran 77 function defining the signature and let f2py generate the Fortran 90 module

      subroutine advance(u, u_1, u_2, f, Cx2, Cy2, dt2, Nx, Ny)
Cf2py intent(c) advance
      integer Nx, Ny, N
      real*8 u(0:Nx,0:Ny), u_1(0:Nx,0:Ny), u_2(0:Nx,0:Ny)
      real*8 f(0:Nx, 0:Ny), Cx2, Cy2, dt2
Cf2py intent(in, out) u
Cf2py intent(c) u, u_1, u_2, f, Cx2, Cy2, dt2, Nx, Ny
      return
      end

Building the extension module

Generate Fortran 90 module (wave2D_u0_loop_c_f2py.pyf):

Terminal> f2py -m wave2D_u0_loop_c_f2py \ 
          -h wave2D_u0_loop_c_f2py.pyf --overwrite-signature \ 
          wave2D_u0_loop_c_f2py_signature.f

The compile and build step must list the C files:

Terminal> f2py -c wave2D_u0_loop_c_f2py.pyf \ 
          --build-dir tmp_build_c \ 
          -DF2PY_REPORT_ON_ARRAY_COPY=1 wave2D_u0_loop_c.c

Migrating loops to C++ via f2py

• C++ can be used as an alternative to C
• C++ code often applies sophisticated arrays
• Challenge: translate from numpy C arrays to C++ array classes
• Can use SWIG to make C++ classes available as Python classes
• Easier (and more efficient):

• Make C API to the C++ code
• Wrap C API with f2py
• Send numpy arrays to C API and let C translate numpy arrays into C++ array classes

Analysis of the difference equations

Properties of the solution of the wave equation

$$ \begin{equation*} \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} \end{equation*} $$

Solutions:

$$ \begin{equation} u(x,t) = g_R(x-ct) + g_L(x+ct), \label{wave:pde1:gensol} \end{equation} $$

If \( u(x,0)=I(x) \) and \( u_t(x,0)=0 \):

$$ \begin{equation} u(x,t) = \half I(x-ct) + \half I(x+ct) \label{wave:pde1:gensol2} \end{equation} $$

Two waves: one traveling to the right and one to the left

Demo of the splitting of \( I(x) \) into two waves

Effect of variable wave velocity

A wave propagates perfectly (\( C=1 \)) and hits a medium with 1/4 of the wave velocity. A part of the wave is reflected and the rest is transmitted.

What happens here?

We have just changed the initial condition...

Representation of waves as sum of sine/cosine waves

Build \( I(x) \) of wave components \( e^{ikx} = \cos kx + i\sin kx \):

$$ \begin{equation} I(x) \approx \sum_{k\in K} b_k e^{ikx} \label{wave:Fourier:I} \end{equation} $$

• \( k \) is the frequency of a component (\( \lambda = 2\pi/k \) corresponding wave length)
• \( K \) is some set of all \( k \) needed to approximate \( I(x) \) well
• \( b_k \) must be computed (Fourier coefficients)

$$ \begin{equation} u(x,t) = \half \sum_{k\in K} b_k e^{ik(x - ct)} + \half \sum_{k\in K} b_k e^{ik(x + ct)} \label{wave:Fourier:u1} \end{equation} $$

Our interest: one component \( e^{i(kx -\omega t)} \), \( \omega = kc \)

Analysis of the finite difference scheme

A similar discrete \( u^n_q = e^{i(kx_q - \tilde\omega t_n)} \) solves

$$ \begin{equation} [D_tD_t u = c^2 D_xD_x u]^n_q \label{wave:pde1:analysis:scheme} \end{equation} $$

Note: different frequency \( \tilde\omega\neq\omega \)

• How accurate is \( \tilde\omega \) compared to \( \omega \)?
• What about the wave amplitude?

Preliminary results

$$ \begin{equation*} [D_tD_t e^{i\omega t}]^n = -\frac{4}{\Delta t^2}\sin^2\left( \frac{\omega\Delta t}{2}\right)e^{i\omega n\Delta t} \end{equation*} $$

By \( \omega\rightarrow k \), \( t\rightarrow x \), \( n\rightarrow q \)) it follows that

$$ \begin{equation*} [D_xD_x e^{ikx}]_q = -\frac{4}{\Delta x^2}\sin^2\left( \frac{k\Delta x}{2}\right)e^{ikq\Delta x} \end{equation*} $$

Numerical wave propagation (1)

Inserting a basic wave component \( u=e^{i(kx_q-\tilde\omega t_n)} \) in the scheme \eqref{wave:pde1:analysis:scheme} requires computation of

$$ \begin{align} \lbrack D_tD_t e^{ikx}e^{-i\tilde\omega t}\rbrack^n_q &= \lbrack D_tD_t e^{-i\tilde\omega t}\rbrack^ne^{ikq\Delta x}\nonumber\\ &= -\frac{4}{\Delta t^2}\sin^2\left( \frac{\tilde\omega\Delta t}{2}\right)e^{-i\tilde\omega n\Delta t}e^{ikq\Delta x}\\ \lbrack D_xD_x e^{ikx}e^{-i\tilde\omega t}\rbrack^n_q &= \lbrack D_xD_x e^{ikx}\rbrack_q e^{-i\tilde\omega n\Delta t}\nonumber\\ &= -\frac{4}{\Delta x^2}\sin^2\left( \frac{k\Delta x}{2}\right)e^{ikq\Delta x}e^{-i\tilde\omega n\Delta t} \end{align} $$

Numerical wave propagation (2)

The complete scheme,

$$ \begin{equation*} \lbrack D_tD_t e^{ikx}e^{-i\tilde\omega t} = c^2D_xD_x e^{ikx}e^{-i\tilde\omega t}\rbrack^n_q \end{equation*} $$

leads to an equation for \( \tilde\omega \):

$$ \begin{equation} \sin^2\left(\frac{\tilde\omega\Delta t}{2}\right) = C^2\sin^2\left(\frac{k\Delta x}{2}\right), \label{wave:pde1:analysis:sineq1} \end{equation} $$ where \( C = \frac{c\Delta t}{\Delta x} \) is the Courant number

Numerical wave propagation (3)

Taking the square root of \eqref{wave:pde1:analysis:sineq1}:

$$ \begin{equation} \sin\left(\frac{\tilde\omega\Delta t}{2}\right) = C\sin\left(\frac{k\Delta x}{2}\right), \label{wave:pde1:analysis:sineq2} \end{equation} $$

• Exact \( \omega \) is real
• Look for a real solution \( \tilde\omega \) of \eqref{wave:pde1:analysis:sineq2}
• Then the sine functions are in \( [-1,1] \)
• Lef-hand side in \( [-1,1] \) requires \( C\leq 1 \)

Why \( C\leq 1 \) is a stability criterion

Assume \( C>1 \). Then

$$ \underbrace{\sin\left(\frac{\tilde\omega\Delta t}{2}\right)}{>1} = C\sin\left(\frac{k\Delta x}{2}\right) $$

• \( |\sin x| >1 \) implies complex \( x \)
• Here: complex \( \tilde\omega = \tilde\omega_r \pm i\tilde\omega_i \)
• One \( \tilde\omega_i < 0 \) gives \( \exp(i\cdot i\tilde\omega_i) = \exp (\tilde\omega_i) \) and exponential growth

Numerical dispersion relation

• How close is \( \tilde\omega \) to \( \omega \)?
• Can solve for an explicit formula for \( \tilde\omega \)

• \( \omega = kc \) is the analytical dispersion relation
• \( \tilde\omega = \tilde\omega(k, c, \Delta x, \Delta t) \) is the numerical dispersion relation
• Speed of waves: \( c=\omega/k \), \( \tilde c = \tilde\omega/k \)
• The numerical wave component has a wrong, mesh-dependent speed

The special case \( C=1 \)

• For \( C=1 \), \( \tilde\omega = \omega \)
• The numerical solution is exact (at the mesh points)!
• The only requirement is constant \( c \)

Computing the error in wave velocity

• Introduce \( p=k\Delta x/2 \)
• \( p \) measures no of mesh points in space per wave length in space
• Study error in wave velocity through \( \tilde c/c \) as function of \( p \)

Visualizing the error in wave velocity

def r(C, p):
    return 2/(C*p)*asin(C*sin(p))

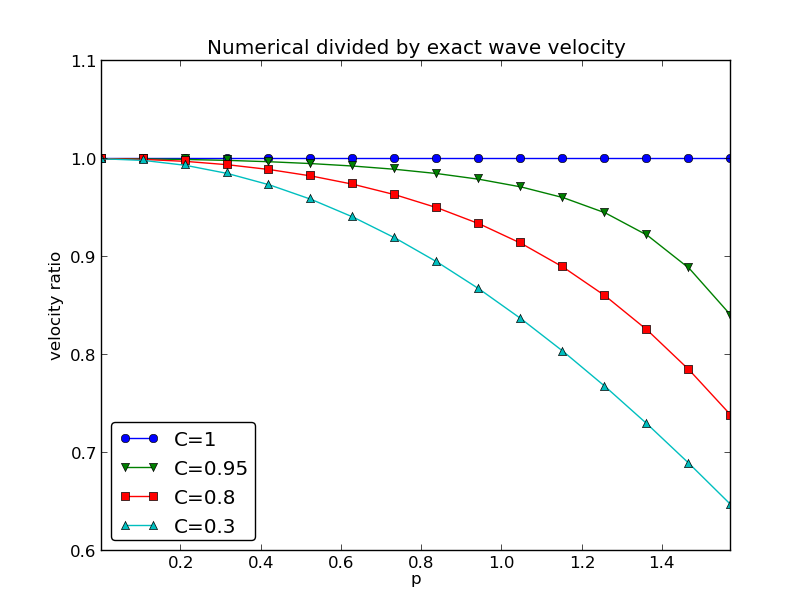
Note: the shortest waves have the largest error, and short waves move too slowly.

Taylor expanding the error in wave velocity

For small \( p \), Taylor expand \( \tilde\omega \) as polynomial in \( p \):

>>> C, p = symbols('C p')
>>> rs = r(C, p).series(p, 0, 7)
>>> print rs
1 - p**2/6 + p**4/120 - p**6/5040 + C**2*p**2/6 -
C**2*p**4/12 + 13*C**2*p**6/720 + 3*C**4*p**4/40 -
C**4*p**6/16 + 5*C**6*p**6/112 + O(p**7)

>>> # Factorize each term and drop the remainder O(...) term
>>> rs_factored = [factor(term) for term in rs.lseries(p)]
>>> rs_factored = sum(rs_factored)
>>> print rs_factored
p**6*(C - 1)*(C + 1)*(225*C**4 - 90*C**2 + 1)/5040 +
p**4*(C - 1)*(C + 1)*(3*C - 1)*(3*C + 1)/120 +
p**2*(C - 1)*(C + 1)/6 + 1

Leading error term is \( \frac{1}{6}(C^2-1)p^2 \) or

$$ \begin{equation} \frac{1}{6}\left(\frac{k\Delta x}{2}\right)^2(C^2-1) = \frac{k^2}{24}\left( c^2\Delta t^2 - \Delta x^2\right) = \Oof{\Delta t^2, \Delta x^2} \end{equation} $$

Example on effect of wrong wave velocity (1)

Smooth wave, few short waves (large \( k \)) in \( I(x) \):

Example on effect of wrong wave velocity (1)

Not so smooth wave, significant short waves (large \( k \)) in \( I(x) \):

Extending the analysis to 2D (and 3D)

$$ u(x,y,t) = g(k_xx + k_yy - \omega t) $$

is a typically solution of

$$ u_{tt} = c^2(u_{xx} + u_{yy}) $$

Can build solutions by adding complex Fourier components of the form

$$ e^{i(k_xx + k_yy - \omega t)} $$

Discrete wave components in 2D

$$ \begin{equation} \lbrack D_tD_t u = c^2(D_xD_x u + D_yD_y u)\rbrack^n_{q,r} \label{wave:pde1:analysis:scheme2D} \end{equation} $$

This equation admits a Fourier component

$$ \begin{equation} u^n_{q,r} = e^{i(k_x q\Delta x + k_y r\Delta y - \tilde\omega n\Delta t)} \label{wave:pde1:analysis:numsol2D} \end{equation} $$

Inserting the expression and using formulas from the 1D analysis:

$$ \begin{equation} \sin^2\left(\frac{\tilde\omega\Delta t}{2}\right) = C_x^2\sin^2 p_x + C_y^2\sin^2 p_y, \end{equation} $$

where

$$ C_x = \frac{c^2\Delta t^2}{\Delta x^2},\quad C_y = \frac{c^2\Delta t^2}{\Delta y^2}, \quad p_x = \frac{k_x\Delta x}{2},\quad p_y = \frac{k_y\Delta y}{2} $$

Stability criterion in 2D

Rreal-valued \( \tilde\omega \) requires

$$ \begin{equation} C_x^2 + C_y^2 \leq 1 \label{wave:pde1:analysis:2DstabC} \end{equation} $$

or

$$ \begin{equation} \Delta t \leq \frac{1}{c} \left( \frac{1}{\Delta x^2} + \frac{1}{\Delta y^2}\right)^{-\halfi} \label{wave:pde1:analysis:2Dstab} \end{equation} $$

Stability criterion in 3D

$$ \begin{equation} \Delta t \leq \frac{1}{c}\left( \frac{1}{\Delta x^2} + \frac{1}{\Delta y^2} + \frac{1}{\Delta z^2}\right)^{-\halfi} \end{equation} $$

For \( c^2=c^2(\xpoint) \) we must use the worst-case value \( \bar c = \sqrt{\max_{\xpoint\in\Omega} c^2(\xpoint)} \) and a safety factor \( \beta\leq 1 \):

$$ \begin{equation} \Delta t \leq \beta \frac{1}{\bar c} \left( \frac{1}{\Delta x^2} + \frac{1}{\Delta y^2} + \frac{1}{\Delta z^2}\right)^{-\halfi} \end{equation} $$

Numerical dispersion relation in 2D (1)

$$ \tilde\omega = \frac{2}{\Delta t}\sin^{-1}\left( \left( C_x^2\sin^2 p_x + C_y^2\sin^ p_y\right)^\half\right) $$

For visualization, introduce \( \theta \):

$$ k_x = k\sin\theta,\quad k_y=k\cos\theta, \quad p_x=\half kh\cos\theta,\quad p_y=\half kh\sin\theta$$

Also: \( \Delta x=\Delta y=h \). Then \( C_x=C_y=c\Delta t/h\equiv C \).

Now \( \tilde\omega \) depends on

• \( C \) reflecting the number cells a wave is displaced during a time step
• \( kh \) reflecting the number of cells per wave length in space
• \( \theta \) expressing the direction of the wave

Numerical dispersion relation in 2D (2)

$$ \frac{\tilde c}{c} = \frac{1}{Ckh} \sin^{-1}\left(C\left(\sin^2 ({\half}kh\cos\theta) + \sin^2({\half}kh\sin\theta) \right)^\half\right) $$

Can make color contour plots of \( 1-\tilde c/c \) in polar coordinates with \( \theta \) as the angular coordinate and \( kh \) as the radial coordinate.

Numerical dispersion relation in 2D (3)