Study guide: Truncation Error Analysis
Sep 24, 2014
Table of contents
Overview of what truncation errors are
Abstract problem setting
Various error measures
Truncation errors in finite difference formulas
Example: The backward difference for \( u'(t) \)
Taylor series
Taylor series inserted in the backward difference approximation
The forward difference for \( u'(t) \)
The central difference for \( u'(t) \) (1)
The central difference for \( u'(t) \) (1)
Leading-order error terms in finite differences (1)
Leading-order error terms in finite differences (2)
Leading-order error terms in mean values (1)
Leading-order error terms in mean values (2)
Software for computing truncation errors
Symbolic computing with difference operators
Truncation errors in exponential decay ODE
Truncation error of the Forward Euler scheme
Truncation error of the Crank-Nicolson scheme
Test the understanding!
Truncation error of the \( \theta \)-rule
Using symbolic software
Empirical verification of the truncation error (1)
Empirical verification of the truncation error (2)
Empirical verification of the truncation error in the Forward Euler scheme
Empirical verification of the truncation error in the Forward Euler scheme
Increasing the accuracy by adding correction terms
Lowering the order of the derivative in the correction term
With a correction term Forward Euler becomes Crank-Nicolson
Correction terms in the Crank-Nicolson scheme (1)
Correction terms in the Crank-Nicolson scheme (2)
Extension to variable coefficients
Exact solutions of the finite difference equations
Computing truncation errors in nonlinear problems (1)
Computing truncation errors in nonlinear problems (2)
Truncation errors in vibration ODEs
Linear model without damping
Truncation errors in the initial condition
Computing correction terms
Model with damping and nonlinearity
Carrying out the truncation error analysis
Extension to quadratic damping
The truncation error for quadratic damping (1)
The truncation error for quadratic damping (2)
The general model formulated as first-order ODEs
The forward-backward scheme
Truncation error analysis
A centered scheme on a staggered mesh
Truncation error analysis (1)
Truncation error analysis (2)
Overview of what truncation errors are
- Definition: The truncation error is the discrepancy that arises from performing a finite number of steps to approximate a process with infinitely many steps.
- Widely used: truncation of infinite series, finite precision arithmetic, finite differences, and differential equations.
- Why? The truncation error is an error measure that is easy to compute.
Abstract problem setting
Consider an abstract differential equation
$$ \mathcal{L}(u)=0\tp$$
Example: \( \mathcal{L}(u)=u'(t)+a(t)u(t)-b(t) \).
The corresponding discrete equation:
$$ \mathcal{L}_{\Delta}(u) =0\tp$$
Let now
- \( u \) be the numerical solution of the discrete equations, computed at mesh points: \( u^n \), \( n=0,\ldots,N_t \)
- \( \uex \) the exact solution of the differential equation
$$
\begin{align*}
\mathcal{L}(\uex)&=0,\\
\mathcal{L}_\Delta(u)&=0\tp
\end{align*}
$$
\( u \) is computed at mesh points
Various error measures
- Dream: the true error \( e = \uex-u \), but usually impossible
- Must find other error measures that are easier to calculate
- Derive formulas for \( u \) in (very) special, simplified cases
- Compute empirical convergence rates for special choices of \( \uex \) (usually non-physical \( \uex \))
- To what extent does \( \uex \) fulfill \( \mathcal{L}_\Delta(\uex)=0 \)?
- It does not fit, but we can measure the error \( \mathcal{L}_\Delta(\uex)=R \)
- \( R \) is the truncation error and it is easy to compute in general, without considering special cases
Truncation errors in finite difference formulas
Example: The backward difference for \( u'(t) \)
Backward difference approximation to \( u' \):
$$
\begin{equation}
\lbrack D_t^- u\rbrack^n = \frac{u^{n} - u^{n-1}}{\Delta t} \approx u'(t_n)
\tag{1}
\tp
\end{equation}
$$
Define the truncation error of this approximation as
$$
\begin{equation}
R^n = [D^-_tu]^n - u'(t_n)\tp
\tag{2}
\end{equation}
$$
The common way of calculating \( R^n \) is to
- expand \( u(t) \) in a Taylor series around the point where the derivative is evaluated, here \( t_n \),
- insert this Taylor series in (2), and
- collect terms that cancel and simplify the expression.
Taylor series
General Taylor series expansion from calculus:
$$ f(x+h) = \sum_{i=0}^\infty \frac{1}{i!}\frac{d^if}{dx^i}(x)h^i\tp $$
Here: expand \( u^{n-1} \) around \( t_n \):
$$
\begin{align*}
u(t_{n-1}) = u(t-\Delta t) &= \sum_{i=0}^\infty \frac{1}{i!}\frac{d^iu}{dt^i}(t_n)(-\Delta t)^i\\
& = u(t_n) - u'(t_n)\Delta t + {\half}u''(t_n)\Delta t^2
+ \Oof{\Delta t^3},
\end{align*}
$$
- \( \Oof{\Delta t^3} \): power-series in \( \Delta t \) where the lowest power is \( \Delta t^3 \)
- Small \( \Delta t \): \( \Delta t \gg \Delta t^3 \gg \Delta t^4 \)
Taylor series inserted in the backward difference approximation
$$
\begin{align*}
[D_t^-u]^n - u'(t_n) &= \frac{u(t_n) - u(t_{n-1})}{\Delta t} - u'(t_n)\\
&= \frac{u(t_n) - (u(t_n) - u'(t_n)\Delta t + {\half}u''(t_n)\Delta t^2 + \Oof{\Delta t^3} )}{\Delta t}\\
&\quad -u'(t_n)\\
&= -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2} )
\end{align*}
$$
Result:
$$
\begin{equation}
R^n = -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2} )
\tp
\end{equation}
$$
The difference approximation is of
first order in \( \Delta t \). It is exact for linear \( \uex \).
The forward difference for \( u'(t) \)
Now consider a forward difference:
$$ u'(t_n) \approx [D_t^+ u]^n = \frac{u^{n+1}-u^n}{\Delta t}\tp$$
Define the truncation error:
$$ R^n = [D_t^+ u]^n - u'(t_n)\tp$$
Expand \( u^{n+1} \) in a Taylor series around \( t_n \),
$$ u(t_{n+1}) = u(t_n) + u'(t_n)\Delta t +
{\half}u''(t_n)\Delta t^2 + \Oof{\Delta t^3}
\tp $$
We get
$$ R = {\half}u''(t_n)\Delta t +
\Oof{\Delta t^2}\tp$$
The central difference for \( u'(t) \) (1)
For the central difference approximation,
$$ u'(t_n)\approx [ D_tu]^n, \quad [D_tu]^n =
\frac{u^{n+\half} - u^{n-\half}}{\Delta t},
$$
the truncation error is
$$ R^n = [ D_tu]^n - u'(t_n)\tp$$
Expand \( u(t_{n+\half}) \) and
\( u(t_{n-1/2}) \) in Taylor series around the point \( t_n \) where
the derivative is evaluated:
$$
\begin{align*}
u(t_{n+\half}) = &u(t_n) + u'(t_n)\half\Delta t +
{\half}u''(t_n)(\half\Delta t)^2 + \\
& \frac{1}{6}u'''(t_n) (\half\Delta t)^3
+ \frac{1}{24}u''''(t_n) (\half\Delta t)^4 + \Oof{\Delta t^5}\\
u(t_{n-1/2}) = &u(t_n) - u'(t_n)\half\Delta t +
{\half}u''(t_n)(\half\Delta t)^2 - \\
& \frac{1}{6}u'''(t_n) (\half\Delta t)^3
+ \frac{1}{24}u''''(t_n) (\half\Delta t)^4 + \Oof{\Delta t^5}
\tp
\end{align*}
$$
The central difference for \( u'(t) \) (1)
$$
u(t_{n+\half}) - u(t_{n-1/2}) = u'(t_n)\Delta t + \frac{1}{24}u'''(t_n) \Delta t^3 + \Oof{\Delta t^5}
\tp
$$
By collecting terms in \( [D_t u]^n - u(t_n) \) we find \( R^n \) to be
$$
\begin{equation}
R^n = \frac{1}{24}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4},
\end{equation}
$$
Note:
- Second-order accuracy since the leading term is \( \Delta t^2 \)
- Only even powers of \( \Delta t \)
Leading-order error terms in finite differences (1)
$$
\begin{align}
\lbrack D_tu \rbrack^n &= \frac{u^{n+\half} - u^{n-\half}}{\Delta t} = u'(t_n) + R^n
\tag{3},\\
R^n &= \frac{1}{24}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{4}\\
\lbrack D_{2t}u \rbrack^n &= \frac{u^{n+1} - u^{n-1}}{2\Delta t} = u'(t_n) + R^n
\tag{5},\\
R^n &= \frac{1}{6}u'''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{6}\\
\lbrack D_t^-u \rbrack^n &= \frac{u^{n} - u^{n-1}}{\Delta t} = u'(t_n) + R^n
\tag{7},\\
R^n &= -{\half}u''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{8}\\
\lbrack D_t^+u \rbrack^n &= \frac{u^{n+1} - u^{n}}{\Delta t} = u'(t_n) + R^n
\tag{9},\\
R^n &= {\half}u''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{10}
\end{align}
$$
Leading-order error terms in finite differences (2)
$$
\begin{align}
[\bar D_tu]^{n+\theta} &= \frac{u^{n+1} - u^{n}}{\Delta t} = u'(t_{n+\theta}) + R^{n+\theta}
\tag{11},\\
R^{n+\theta} &= \half(1-2\theta)u''(t_{n+\theta})\Delta t -
\frac{1}{6}((1 - \theta)^3 - \theta^3)u'''(t_{n+\theta})\Delta t^2 +
\Oof{\Delta t^3}
\tag{12}\\
\lbrack D_t^{2-}u \rbrack^n &= \frac{3u^{n} - 4u^{n-1} + u^{n-2}}{2\Delta t} = u'(t_n) + R^n
\tag{13},\\
R^n &= -\frac{1}{3}u'''(t_n)\Delta t^2 + \Oof{\Delta t^3}
\tag{14}\\
\lbrack D_tD_t u \rbrack^n &= \frac{u^{n+1} - 2u^{n} + u^{n-1}}{\Delta t^2} = u''(t_n) + R^n
\tag{15},\\
R^n &= \frac{1}{12}u''''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tag{16}
\end{align}
$$
Leading-order error terms in mean values (1)
Weighted arithmetic mean:
$$
\begin{align}
[\overline{u}^{t,\theta}]^{n+\theta}
& = \theta u^{n+1} + (1-\theta)u^n =
u(t_{n+\theta}) + R^{n+\theta},
\tag{17}\\
R^{n+\theta} &= {\half}u''(t_{n+\theta})\Delta t^2\theta (1-\theta) +
\Oof{\Delta t^3}
\tp
\tag{18}
\end{align}
$$
Standard arithmetic mean:
$$
\begin{align}
[\overline{u}^{t}]^{n} &= \half(u^{n-\half} + u^{n+\half})
= u(t_n) + R^{n},
\tag{19}\\
R^{n} &= \frac{1}{8}u''(t_{n})\Delta t^2 + \frac{1}{384}u''''(t_n)\Delta t^4
+ \Oof{\Delta t^6}\tp
\tag{20}
\end{align}
$$
Leading-order error terms in mean values (2)
Geometric mean:
$$
\begin{align}
[\overline{u^2}^{t,g}]^{n} &= u^{n-\half}u^{n+\half} = (u^n)^2 + R^n,
\tag{21}\\
R^n &= - \frac{1}{4}u'(t_n)^2\Delta t^2 + \frac{1}{4}u(t_n)u''(t_n)\Delta t^2
+ \Oof{\Delta t^4}
\tp
\tag{22}
\end{align}
$$
Harmonic mean:
$$
\begin{align}
[\overline{u}^{t,h}]^{n} &= u^n = \frac{2}{\frac{1}{u^{n-\half}} + \frac{1}{u^{n+\half}}}
+ R^{n+\half},
\tag{23}\\
R^n &= - \frac{u'(t_n)^2}{4u(t_n)}\Delta t^2 + \frac{1}{8}u''(t_n)\Delta t^2
\tp
\tag{24}
\end{align}
$$
Software for computing truncation errors
- Can use
sympyto automate calculations with Taylor series. - Tool: course module
truncation_errors
>>> from truncation_errors import TaylorSeries
>>> from sympy import *
>>> u, dt = symbols('u dt')
>>> u_Taylor = TaylorSeries(u, 4)
>>> u_Taylor(dt)
D1u*dt + D2u*dt**2/2 + D3u*dt**3/6 + D4u*dt**4/24 + u
>>> FE = (u_Taylor(dt) - u)/dt
>>> FE
(D1u*dt + D2u*dt**2/2 + D3u*dt**3/6 + D4u*dt**4/24)/dt
>>> simplify(FE)
D1u + D2u*dt/2 + D3u*dt**2/6 + D4u*dt**3/24
Notation: D1u for \( u' \), D2u for \( u'' \), etc.
See trunc/truncation_errors.py.
Symbolic computing with difference operators
A class DiffOp represents many common difference operators:
>>> from truncation_errors import DiffOp
>>> from sympy import *
>>> u = Symbol('u')
>>> diffop = DiffOp(u, independent_variable='t')
>>> diffop['geometric_mean']
-D1u**2*dt**2/4 - D1u*D3u*dt**4/48 + D2u**2*dt**4/64 + ...
>>> diffop['Dtm']
D1u + D2u*dt/2 + D3u*dt**2/6 + D4u*dt**3/24
>>> diffop.operator_names()
['geometric_mean', 'harmonic_mean', 'Dtm', 'D2t', 'DtDt',
'weighted_arithmetic_mean', 'Dtp', 'Dt']
Names in diffop:
Dtp for \( D^+_t \), Dtm for \( D_t^- \), Dt for \( D_t \), D2t for
\( D_{2t} \), DtDt for \( D_tD_t \).
Truncation errors in exponential decay ODE
$$
u'(t)=-au(t)
$$
Truncation error of the Forward Euler scheme
The Forward Euler scheme:
$$
\begin{equation}
\lbrack D_t^+ u = -au \rbrack^n
\tag{25}
\tp
\end{equation}
$$
Definition of the truncation error \( R^n \):
$$
\begin{equation}
\lbrack D_t^+ \uex + a\uex = R \rbrack^n
\tag{26}
\tp
\end{equation}
$$
$$ [D_t^+ \uex]^n = \uex'(t_n) +
\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}\tp$$
Inserted in (26):
$$
\uex'(t_n) +
\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
+ a\uex(t_n) = R^n
\tp
$$
Note: \( \uex'(t_n) + a\uex^n = 0 \) since \( \uex \) solves the ODE. Then
$$
\begin{equation}
R^n = \half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{27}
\tp
\end{equation}
$$
Truncation error of the Crank-Nicolson scheme
Crank-Nicolson:
$$
\begin{equation}
[D_t u = -au]^{n+\half},
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_t \uex + a\overline{\uex}^{t} = R]^{n+\half}
\tp
\tag{28}
\end{equation}
$$
$$
\begin{align*}
\lbrack D_t\uex \rbrack^{n+\half} &= u'(t_{n+\half}) +
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2 + \Oof{\Delta t^4},\\
[a\overline{\uex}^{t}]^{n+\half}
&= u(t_{n+\half}) + \frac{1}{8}u''(t_{n})\Delta t^2 +
+ \Oof{\Delta t^4}
\end{align*}
$$
Inserted in the scheme we get
$$
\begin{equation}
R^{n+\half} = \left(
\frac{1}{24}\uex'''(t_{n+\half}) + \frac{1}{8}u''(t_{n})
\right)\Delta t^2 + \Oof{\Delta t^4}
\end{equation}
$$
\( R^n = \Oof{\Delta t^2} \) (second-order scheme)
Test the understanding!
Analyze the the truncation error of the Backward Euler scheme and show that it is \( \Oof{\Delta t} \) (first order scheme).
Truncation error of the \( \theta \)-rule
The \( \theta \)-rule:
$$
[\bar D_t u = -a\overline{u}^{t,\theta}]^{n+\theta}
\tp
$$
Truncation error:
$$
[\bar D_t \uex + a\overline{\uex}^{t,\theta} = R]^{n+\theta}
\tp
$$
Use (11)-(12) and (17)-(18) along with
\( \uex'(t_{n+\theta}) + a\uex(t_{n+\theta})=0 \) to show
$$
\begin{align}
R^{n+\theta}
=
&({\half}-\theta)\uex''(t_{n+\theta})\Delta t +
\half\theta (1-\theta)\uex''(t_{n+\theta})\Delta t^2 + \nonumber\\
& \half(\theta^2 -\theta + 3)\uex'''(t_{n+\theta})\Delta t^2
+ \Oof{\Delta t^3}
\end{align}
$$
Note: 2nd-order scheme if and only if \( \theta =1/2 \).
Using symbolic software
Can use sympy and the tools in
truncation_errors.py:
def decay():
u, a = sm.symbols('u a')
diffop = DiffOp(u, independent_variable='t',
num_terms_Taylor_series=3)
D1u = diffop.D(1) # symbol for du/dt
ODE = D1u + a*u # define ODE
# Define schemes
FE = diffop['Dtp'] + a*u
CN = diffop['Dt' ] + a*u
BE = diffop['Dtm'] + a*u
# Residuals (truncation errors)
R = {'FE': FE-ODE, 'BE': BE-ODE, 'CN': CN-ODE}
return R
The returned dictionary becomes
decay: {
'BE': D2u*dt/2 + D3u*dt**2/6,
'FE': -D2u*dt/2 + D3u*dt**2/6,
'CN': D3u*dt**2/24,
}
\( \theta \)-rule: see truncation_errors.py (long expression, very advantageous
to automate the math!)
Empirical verification of the truncation error (1)
Ideas:
- Compute \( R^n \) numerically
- Run a sequence of meshes
- Estimate the convergence rate of \( R^n \)
For the Forward Euler scheme:
$$
\begin{equation}
R^n = \lbrack D_t^+\uex + a\uex \rbrack^n
\tag{29}
\tp
\end{equation}
$$
Insert correct \( \uex(t)=Ie^{-at} \) (or use method of manufactured solution
in more general cases).
Empirical verification of the truncation error (2)
- Assume \( R^n = C\Delta t^r \)
- \( C \) and \( r \) will vary with \( n \) - must estimate \( r \) for each mesh point
- Use a sequence of meshes with \( N_t = 2^{-k}N_0 \) intervals, \( k=1,2,\ldots \)
- Transform \( R^n \) data to the coarsest mesh and estimate \( r \) for each coarse mesh point
See the text for more details and an implementation.
Empirical verification of the truncation error in the Forward Euler scheme
Figure 1: Estimated truncation error at mesh points for different meshes.
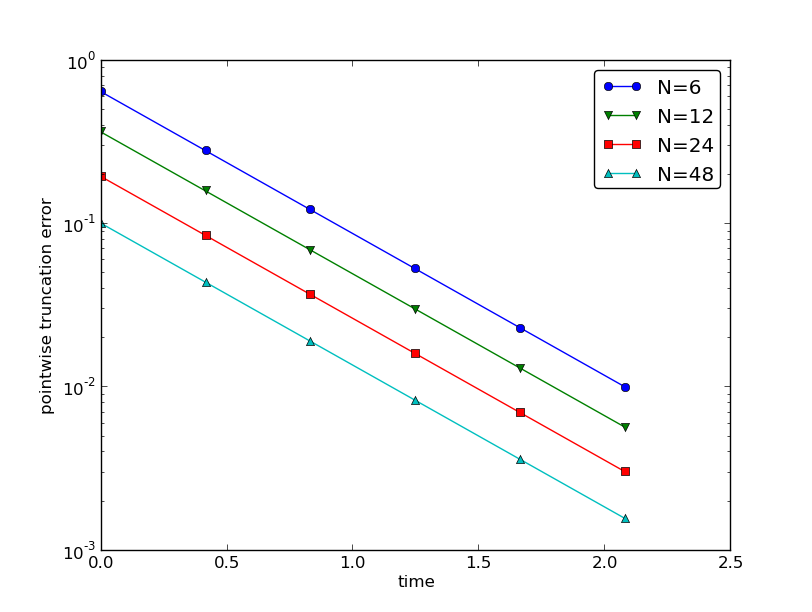
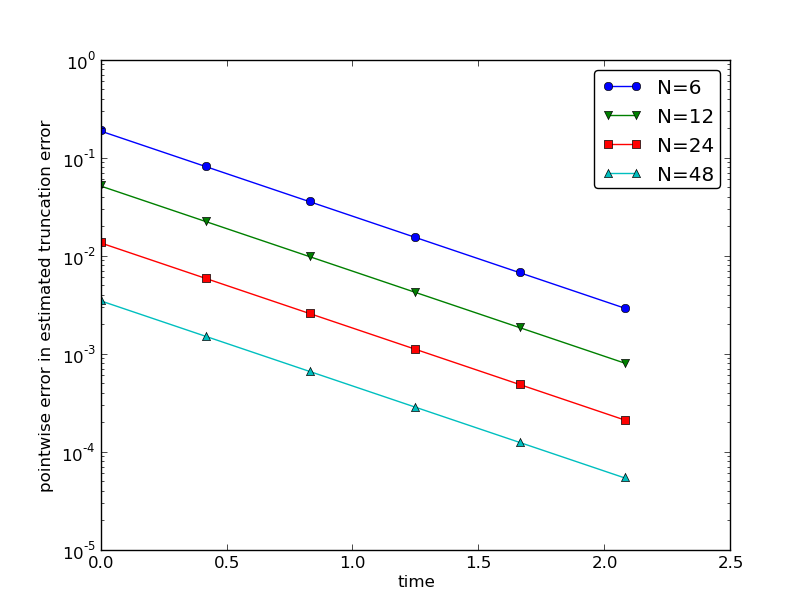
Empirical verification of the truncation error in the Forward Euler scheme
Figure 2: Difference between theoretical and estimated truncation error at mesh points for different meshes.
Increasing the accuracy by adding correction terms
Can we add terms in the differential equation that can help increase the order of the truncation error?
To be precise for the Forward Euler scheme, can we find \( C \) to make \( R \) $\Oof{\Delta t^2}$?
$$
\begin{equation}
\lbrack D_t^+ \uex + a\uex = C + R \rbrack^n\tp
\tag{30}
\end{equation}
$$
$$
\half\uex''(t_n)\Delta t - \frac{1}{6}\uex'''(t_n)\Delta t^2
+ \Oof{\Delta t^3} = C^n + R^n\tp$$
Choosing
$$ C^n = \half\uex''(t_n)\Delta t,$$
makes
$$ R^n = \frac{1}{6}\uex'''(t_n)\Delta t^2 + \Oof{\Delta t^3}\tp$$
Lowering the order of the derivative in the correction term
- \( C^n \) contains \( u'' \)
- Can discretize \( u'' \) (requires \( u^{n+1} \), \( u^n \), and \( u^{n-1} \))
- Can also express \( u'' \) in terms of \( u' \) or \( u \)
$$ u' = -au,\quad\Rightarrow\quad u''=-au'=a^2u\tp$$
Result for \( u''=a^2u \): apply Forward Euler to a perturbed ODE,
$$
\begin{equation}
u' = -\hat au ,\quad \hat a = a(1 - {\half}a\Delta t),
\tag{31}
\end{equation}
$$
to make a second-order scheme!
With a correction term Forward Euler becomes Crank-Nicolson
Use the other alternative \( u''=-au' \):
$$ u'=-au - {\half}a\Delta t u'\quad\Rightarrow\quad
\left( 1 + {\half}a\Delta t\right) u' = -au\tp$$
Apply Forward Euler:
$$
\left( 1 + {\half}a\Delta t\right)\frac{u^{n+1}-u^n}{\Delta t}
= -au^n,$$
which after some algebra can be written as
$$ u^{n+1} = \frac{1 - {\half}a\Delta t}{1+{\half}a\Delta t}u^n\tp$$
This is a Crank-Nicolson scheme (of second order)!
Correction terms in the Crank-Nicolson scheme (1)
$$ [D_t u = -a\overline{u}^t]^{n+\half},$$
Definition of the truncation error \( R \) and correction terms \( C \):
$$ [D_t \uex + a\overline{\uex}^{t} = C + R]^{n+\half}\tp$$
Must Taylor expand
- the derivative
- the arithmetic mean
$$
C^{n+\half} + R^{n+\half} =
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
+ \frac{a}{8}\uex''(t_{n+\half})\Delta t^2 + \Oof{\Delta t^4}\tp$$
Let \( C^{n+\half} \) cancel the \( \Delta t^2 \) terms:
$$ C^{n+\half} =
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
+ \frac{a}{8}\uex''(t_{n})\Delta t^2\tp$$
Correction terms in the Crank-Nicolson scheme (2)
- Must replace \( u''' \) and \( u'' \) in correction term
- Using \( u'=-au \): \( u''=a^2u \) and \( u'''=-a^3u \)
Result: solve the perturbed ODE by a Crank-Nicolson method,
$$ u' = -\hat a u,\quad \hat a = a(1 - \frac{1}{12}a^2\Delta t^2)\tp$$
and experience an error \( \Oof{\Delta t^4} \).
Extension to variable coefficients
$$ u'(t) = -a(t)u(t) + b(t)$$
Forward Euler:
$$
\begin{equation}
[D_t^+ u = -au + b]^n
\tp
\end{equation}
$$
The truncation error is found from
$$
\begin{equation}
[D_t^+ \uex + a\uex - b = R]^n
\tp
\end{equation}
$$
$$ \uex'(t_n) - \half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
+ a(t_n)\uex(t_n) - b(t_n) = R^n
\tp
$$
Because of the ODE, \( \uex'(t_n) + a(t_n)\uex(t_n) - b(t_n) =0 \), and
$$
\begin{equation}
R^n = -\half\uex''(t_n)\Delta t + \Oof{\Delta t^2}
\tag{32}
\tp
\end{equation}
$$
No problems with variable coefficients!
Exact solutions of the finite difference equations
How does the truncation error depend on \( \uex \) in finite differences?
- One-sided differences: \( \uex''\Delta t \) (lowest order)
- Centered differences: \( \uex'''\Delta t^2 \) (lowest order)
- Only harmonic and geometric mean involve \( \uex' \) or \( \uex \)
Consequence:
- \( \uex(t)=ct+d \) will very often give exact solution of the discrete equations (\( R=0 \))!
- Ideal for verification
- Centered schemes allow quadratic \( \uex \)
Problem: harmonic and geometric mean (error depends on \( \uex' \) and \( \uex \))
Computing truncation errors in nonlinear problems (1)
$$
\begin{equation}
u'=f(u,t)
\tag{33}
\end{equation}
$$
Crank-Nicolson scheme:
$$
\begin{equation}
[D_t u'=\overline{f}^{t}]^{n+\half}\tp
\tag{33}
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_t \uex' - \overline{f}^{t}= R]^{n+\half}\tp
\tag{35}
\end{equation}
$$
Using (19)-(20) for the arithmetic mean:
$$
\begin{align*}
\lbrack\overline{f}^{t}\rbrack^{n+\half} &=
\half(f(\uex^n,t_n) + f(\uex^{n+1},t_{n+1}))\\
&= f(\uex^{n+\half},t_{n+\half}) +
\frac{1}{8}\uex''(t_{n+\half})\Delta t^2
+ \Oof{\Delta t^4}\tp
\end{align*}
$$
Computing truncation errors in nonlinear problems (2)
With (3)-(4), (35) leads to \( R^{n+\half} \) equal to
$$
\uex'(t_{n+\half}) +
\frac{1}{24}\uex'''(t_{n+\half})\Delta t^2
- f(\uex^{n+\half},t_{n+\half}) -
\frac{1}{8}\uex''(t_{n+\half})\Delta t^2
+ \Oof{\Delta t^4} \tp
$$
Since \( \uex'(t_{n+\half}) - f(\uex^{n+\half},t_{n+\half})=0 \),
the truncation error becomes
$$ R^{n+\half} = (\frac{1}{24}\uex'''(t_{n+\half})
- \frac{1}{8}\uex''(t_{n+\half})) \Delta t^2\tp
$$
The computational techniques worked well
even for this nonlinear ODE!
Truncation errors in vibration ODEs
Linear model without damping
$$
\begin{equation}
u''(t) + \omega^2 u(t) = 0,\quad u(0)=I,\ u'(0)=0\tp
\tag{36}
\end{equation}
$$
Centered difference approximation:
$$
\begin{equation}
[D_tD_t u + \omega^2u=0]^n
\tag{37}
\tp
\end{equation}
$$
Truncation error:
$$
\begin{equation}
[D_tD_t \uex + \omega^2\uex =R]^n
\tp
\end{equation}
$$
Use (15)-(16) to expand \( [D_t D_t\uex]^n \):
$$ [D_tD_t \uex]^n = \uex''(t_n) + \frac{1}{12}\uex''''(t_n)\Delta t^2,$$
Collect terms: \( \uex''(t) + \omega^2\uex(t)=0 \). Then,
$$
\begin{equation}
R^n = \frac{1}{12}\uex''''(t_n)\Delta t^2 + \Oof{\Delta t^4}
\tp
\end{equation}
$$
Truncation errors in the initial condition
- Initial conditions: \( u(0)=I \), \( u'(0)=V \)
- Need discretization of \( u'(0) \)
- Standard, centered difference: \( [D_{2t} u=V]^0 \), \( R^0=\Oof{\Delta t^2} \)
- Simpler, forward difference: \( [D_t^+u=V]^0 \), \( R^0=\Oof{\Delta t} \)
- Does the lower order of the forward scheme impact the order of the whole simulation?
- Answer: run experiments!
Computing correction terms
- Can we add terms to the ODE such that the truncation error is improved?
$$ [D_tD_t \uex + \omega^2\uex =C + R]^n,$$
- Idea: choose \( C^n \) such that it absorbs the \( \Delta t^2 \) term in \( R^n \),
$$ C^n = \frac{1}{12}\uex''''(t_n)\Delta t^2\tp$$
- Downside: got a \( u'''' \) term
- Remedy: use the ODE \( u''=-\omega^2u \) to see that \( u'''' = \omega^4 u \).
- Just apply the standard scheme to a modified ODE:
$$ [D_tD_t u + \omega^2(1 - \frac{1}{12}\omega^2\Delta t^2)u=0]^n,$$
- Accuracy is \( \Oof{\Delta t^4} \).
Model with damping and nonlinearity
Linear damping \( \beta u' \), nonlinear spring force \( s(u) \), and excitation \( F \):
$$
\begin{equation}
mu'' + \beta u' + s(u) =F(t)\tp
\tag{38}
\end{equation}
$$
Central difference discretization:
$$
\begin{equation}
[mD_tD_t u + \beta D_{2t} u + s(u)=F]^n
\tp
\end{equation}
$$
Truncation error is defined by
$$
\begin{equation}
[mD_tD_t \uex + \beta D_{2t} \uex + s(\uex)=F + R]^n
\tp
\end{equation}
$$
Carrying out the truncation error analysis
Using (15)-(16) and (5)-(6) we get
$$
\begin{align*}
\lbrack mD_tD_t \uex + \beta D_{2t} \uex\rbrack^n &=
m\uex''(t_n) + \beta\uex'(t_n) + \\
&\quad \left(\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{6}\uex'''(t_n)\right)\Delta t^2 + \Oof{\Delta t^4}
\end{align*}
$$
The terms
$$ m\uex''(t_n) + \beta\uex'(t_n) + \omega^2\uex(t_n) + s(\uex(t_n)) - F^n,$$
correspond to the ODE (= zero).
Result: accuracy of \( \Oof{\Delta t^2} \) since
$$
\begin{equation}
R^n = \left(\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{6}\uex'''(t_n)\right)\Delta t^2 + \Oof{\Delta t^4},
\tag{39}
\end{equation}
$$
Correction terms: complicated when the ODE has many terms...
Extension to quadratic damping
$$
\begin{equation}
mu'' + \beta |u'|u' + s(u) =F(t)\tp
\tag{40}
\end{equation}
$$
Centered scheme: \( |u'|u' \) gives rise to a nonlinearity.
Linearization trick: use a geometric mean,
$$ [|u'|u']^n \approx |[u']^{n-\half}|[u']^{n+\half}\tp$$
Scheme:
$$
\begin{equation}
[mD_t D_t u]^n + \beta |[D_{t} u]^{n-\half}|[D_t u]^{n+\half}
+ s(u^n)=F^n\tp
\end{equation}
$$
The truncation error for quadratic damping (1)
Definition of \( R^n \):
$$
\begin{equation}
[mD_t D_t \uex]^n +
\beta |[D_{t} \uex]^{n-\half}|[D_t \uex]^{n+\half}
+ s(\uex^n)-F^n = R^n\tp
\end{equation}
$$
Truncation error of the geometric mean, see (21)-(22),
$$
\begin{align*}
|[D_{t} \uex]^{n-\half}|[D_t \uex]^{n+\half}
&= [|D_t\uex|D_t\uex]^n
- \frac{1}{4}u'(t_n)^2\Delta t^2 + \\
&\quad \frac{1}{4}u(t_n)u''(t_n)\Delta t^2
+ \Oof{\Delta t^4}\tp
\end{align*}
$$
Using (3)-(4) for the \( D_t\uex \) factors results in
$$
\begin{align*}
[|D_t\uex|D_t\uex]^n &= |\uex' + \frac{1}{24}\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4}|\times\\
&\quad (\uex' + \frac{1}{24}\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4})
\end{align*}
$$
The truncation error for quadratic damping (2)
For simplicity, remove the absolute value. The product becomes
$$
[D_t\uex D_t\uex]^n = (\uex'(t_n))^2 +
\frac{1}{12}\uex(t_n)\uex'''(t_n)\Delta t^2 +
\Oof{\Delta t^4}\tp$$
With
$$ m[D_t D_t\uex]^n = m\uex''(t_n) + \frac{m}{12}\uex''''(t_n)\Delta t^2
+\Oof{\Delta t^4},$$
and using \( mu'' + \beta (u')^2 + s(u)=F \), we end up with
$$ R^n = (\frac{m}{12}\uex''''(t_n) +
\frac{\beta}{12}\uex(t_n)\uex'''(t_n))
\Delta t^2 + \Oof{\Delta t^4}\tp$$
Second-order accuracy! Thanks to
- difference approximation with error \( \Oof{\Delta t^2} \)
- geometric mean approximation with error \( \Oof{\Delta t^2} \)
The general model formulated as first-order ODEs
$$
\begin{equation}
mu'' + \beta |u'|u' + s(u) =F(t)\tp
\tag{40}
\end{equation}
$$
Rewritten as first-order system:
$$
\begin{align}
u' &= v,
\tag{42} \\
v' &= \frac{1}{m}\left( F(t) - \beta |v|v - s(u)\right)\tp
\tag{43}
\end{align}
$$
To solution methods:
- Forward-backward scheme
- Centered scheme on a staggered mesh
The forward-backward scheme
Forward step for \( u \), backward step for \( v \):
$$
\begin{align}
[D_t^+ u &= v]^n,
\tag{44} \\
[D_t^-v &= \frac{1}{m}( F(t) - \beta |v|v - s(u))]^{n+1}\tp
\tag{45}
\end{align}
$$
- Note:
- Problem: \( |v|v \) gives nonlinearity \( |v^{n+1}|v^{n+1} \).
- Remedy: linearized as \( |v^{n}|v^{n+1} \)
$$
\begin{align}
[D_t^+ u &= v]^n,
\tag{46} \\
[D_t^-v]^{n+1} &= \frac{1}{m}( F(t_{n+1}) - \beta |v^n|v^{n+1} - s(u^{n+1}))\tp
\tag{47}
\end{align}
$$
Truncation error analysis
- Aim (as always): turn difference operators into derivatives + truncation error terms
- One-sided forward/backward differences: error \( \Oof{\Delta t} \)
- Linearization of \( |v^{n+1}|v^{n+1} \) to \( |v^n|v^{n+1} \): error \( \Oof{\Delta t} \)
- All errors are \( \Oof{\Delta t} \)
- First-order scheme? No!
- "Symmetric" use of the \( \Oof{\Delta t} \) building blocks yields in fact a \( \Oof{\Delta t^2} \) scheme (!)
- Why? See next slide...
A centered scheme on a staggered mesh
Staggered mesh:
- \( u \) is computed at mesh points \( t_n \)
- \( v \) is computed at points \( t_{n+\half} \)
Centered differences in (42)-(42):
$$
\begin{align}
[D_t u &= v]^{n-\half},
\tag{48} \\
[D_t v &= \frac{1}{m}( F(t) - \beta |v|v - s(u))]^{n}\tp
\tag{49}
\end{align}
$$
- Problem: \( |v^n|v^n \), because \( v^n \) is not computed directly
- Remedy: Geometric mean,
$$ |v^n|v^n \approx |v^{n-\half}|v^{n+\half}\tp$$
Truncation error analysis (1)
Resulting scheme:
$$
\begin{align}
[D_t u]^{n-\half} &= v^{n-\half},
\tag{50} \\
[D_t v]^n &= \frac{1}{m}( F(t_n) -
\beta |v^{n-\half}|v^{n+\half} - s(u^n))\tp
\tag{51}
\end{align}
$$
The truncation error in each equation is found from
$$
\begin{align*}
[D_t \uex]^{n-\half} &= \vex(t_{n-\half}) + R_u^{n-\half},\\
[D_t \vex]^n &= \frac{1}{m}( F(t_n) -
\beta |\vex(t_{n-\half})|\vex(t_{n+\half}) - s(u^n)) + R_v^n\tp
\end{align*}
$$
Using (3)-(4) for derivatives and (21)-(22)
for the geometric mean:
$$
\uex'(t_{n-\half}) +
\frac{1}{24}\uex'''(t_{n-\half})\Delta t^2 + \Oof{\Delta t^4}
= \vex(t_{n-\half}) + R_u^{n-\half},$$
and
$$
\vex'(t_n) =
\frac{1}{m}( F(t_n) -
\beta |\vex(t_n)|\vex(t_n) + \Oof{\Delta t^2} - s(u^n)) + R_v^n\tp
$$
Truncation error analysis (2)
Resulting truncation error is \( \Oof{\Delta t^2} \):
$$ R_u^{n-\half}= \Oof{\Delta t^2}, \quad R_v^n = \Oof{\Delta t^2}\tp$$
Comparing The schemes (50)-(51) and (46)-(47) are equivalent. Therefore, the forward/backward scheme with ad hoc linearization is also \( \Oof{\Delta t^2} \)!