Study guide: Intro to Computing with Finite Difference Methods
Oct 5, 2014
INF5620 in a nutshell
- Numerical methods for partial differential equations (PDEs)
- How do we solve a PDE in practice and produce numbers?
- How do we trust the answer?
- Approach: simplify, understand, generalize
You see a PDE and can't wait to program a method and visualize a solution! Somebody asks if the solution is right and you can give a convincing answer.
The new official six-point course description
After having completed INF5620 you
- can derive methods and implement them to solve frequently arising partial differential equations (PDEs) from physics and mechanics.
- have a good understanding of finite difference and finite element methods and how they are applied in linear and nonlinear PDE problems.
- can identify numerical artifacts and perform mathematical analysis to understand and cure non-physical effects.
- can apply sophisticated programming techniques in Python, combined with Cython, C, C++, and Fortran code, to create modern, flexible simulation programs.
- can construct verification tests and automate them.
- have experience with project hosting sites (GitHub), version control systems (Git), report writing (LaTeX), and Python scripting for performing reproducible computational science.
More specific contents: finite difference methods
- ODEs
- the wave equation \( u_{tt}=u_{xx} \) in 1D, 2D, 3D
- the diffusion equation \( u_t=u_{xx} \) in 1D, 2D, 3D
- write your own software from scratch
- understand how the methods work and why they fail
More specific contents: finite element methods
- stationary diffusion equations \( u_{xx}=f \) in 1D
- time-dependent diffusion and wave equations in 1D
- PDEs in 2D and 3D by use of the FEniCS software
- perform hand-calculations, write your own software (1D)
- understand how the methods work and why they fail
More specific contents: nonlinear and advanced problems
- Nonlinear PDEs
- Newton and Picard iteration methods, finite differences and elements
- More advanced PDEs for fluid flow and elasticity
- Parallel computing
Philosophy: simplify, understand, generalize
- Start with simplified ODE/PDE problems
- Learn to reason about the discretization
- Learn to implement, verify, and experiment
- Understand the method, program, and results
- Generalize the problem, method, and program
This is the power of applied mathematics!
The exam
- Oral exam
- 6 problems (topics) are announced two weeks before the exam
- Work out a 20 min presentations (talks) for each problem
- At the exam: throw a die to pick your problem to be presented
- Aids: plots, computer programs
- Why? Very effective way of learning
- Sure? Excellent results over 15 years
- When? Late december
Required software
- Our software platform: Python (sometimes combined with Cython, Fortran, C, C++)
- Important Python packages:
numpy,scipy,matplotlib,sympy,fenics,scitools, ... - Suggested installation: Run Ubuntu in a virtual machine
- Alternative: run a Vagrant machine
Assumed/ideal background
- INF1100: Python programming, solution of ODEs
- Some experience with finite difference methods
- Some analytical and numerical knowledge of PDEs
- Much experience with calculus and linear algebra
- Much experience with programming of mathematical problems
- Experience with mathematical modeling with PDEs (from physics, mechanics, geophysics, or ...)
Start-up example for the course
What if you don't have this ideal background?
- Students come to this course with very different backgrounds
- First task: summarize assumed background knowledge by going through a simple example
- Also in this example:
- Some fundamental material on software implementation and software testing
- Material on analyzing numerical methods to understand why they can fail
- Applications to real-world problems
Start-up example
$$ u'=-au,\quad u(0)=I,\ t\in (0,T],$$
where \( a>0 \) is a constant.
Everything we do is motivated by what we need as building blocks for solving PDEs!
What to learn in the start-up example; standard topics
- How to think when constructing finite difference methods, with special focus on the Forward Euler, Backward Euler, and Crank-Nicolson (midpoint) schemes
- How to formulate a computational algorithm and translate it into Python code
- How to make curve plots of the solutions
- How to compute numerical errors
- How to compute convergence rates
What to learn in the start-up example; programming topics
- How to verify an implementation and automate verification through nose tests in Python
- How to structure code in terms of functions, classes, and modules
- How to work with Python concepts such as arrays, lists, dictionaries, lambda functions, functions in functions (closures), doctests, unit tests, command-line interfaces, graphical user interfaces
- How to perform array computing and understand the difference from scalar computing
- How to conduct and automate large-scale numerical experiments
- How to generate scientific reports
What to learn in the start-up example; mathematical analysis
- How to uncover numerical artifacts in the computed solution
- How to analyze the numerical schemes mathematically to understand why artifacts occur
- How to derive mathematical expressions for various measures of
the error in numerical methods, frequently by using the
sympysoftware for symbolic computation - Introduce concepts such as finite difference operators, mesh (grid), mesh functions, stability, truncation error, consistency, and convergence
What to learn in the start-up example; generalizations
- Generalize the example to \( u'(t)=-a(t)u(t) + b(t) \)
- Present additional methods for the general nonlinear ODE \( u'=f(u,t) \), which is either a scalar ODE or a system of ODEs
- How to access professional packages for solving ODEs
- How our model equations like \( u'=-au \) arises in a wide range of phenomena in physics, biology, and finance
Finite difference methods
- The finite difference method is the simplest method for solving differential equations
- Fast to learn, derive, and implement
- A very useful tool to know, even if you aim at using the finite element or the finite volume method
Topics in the first intro to the finite difference method
- How to think about finite difference discretization
- Key concepts:
- mesh
- mesh function
- finite difference approximations
- The Forward Euler, Backward Euler, and Crank-Nicolson methods
- Finite difference operator notation
- How to derive an algorithm and implement it in Python
- How to test the implementation
A basic model for exponential decay
The world's simplest (?) ODE:
$$
\begin{equation*}
u'(t) = -au(t),\quad u(0)=I,\ t\in (0,T]
\end{equation*}
$$
We can learn a lot about numerical methods, computer implementation, program testing, and real applications of these tools by using this very simple ODE as example. The teaching principle is to keep the math as simple as possible while learning computer tools.
The ODE model has a range of applications in many fields
- Growth and decay of populations (cells, animals, human)
- Growth and decay of a fortune
- Radioactive decay
- Cooling/heating of an object
- Pressure variation in the atmosphere
- Vertical motion of a body in water/air
- Time-discretization of diffusion PDEs by Fourier techniques
See the text for details.
The ODE problem has a continuous and discrete version
Continuous problem
$$
\begin{equation}
u' = -au,\ t\in (0,T], \quad u(0)=I
\tag{1}
\end{equation}
$$
(varies with a continuous \( t \))
Discrete problem
Numerical methods applied to the continuous problem turns it into a discrete problem
$$
\begin{equation}
u^{n+1} = \mbox{const} u^n, \quad n=0,1,\ldots N_t-1, \quad u^n=I
\tag{2}
\end{equation}
$$
(varies with discrete mesh points \( t_n \))
The steps in the finite difference method
Solving a differential equation by a finite difference method consists of four steps:
- discretizing the domain,
- fulfilling the equation at discrete time points,
- replacing derivatives by finite differences,
- formulating a recursive algorithm.
Step 1: Discretizing the domain
The time domain \( [0,T] \) is represented by a mesh: a finite number of \( N_t+1 \) points
$$0 = t_0 < t_1 < t_2 < \cdots < t_{N_t-1} < t_{N_t} = T$$
- We seek the solution \( u \) at the mesh points: \( u(t_n) \), \( n=1,2,\ldots,N_t \).
- Note: \( u^0 \) is known as \( I \).
- Notational short-form for the numerical approximation to \( u(t_n) \): \( u^n \)
- In the differential equation: \( u \) is the exact solution
- In the numerical method and implementation: \( u^n \) is the numerical approximation, \( \uex(t) \) is the exact solution
Step 1: Discretizing the domain
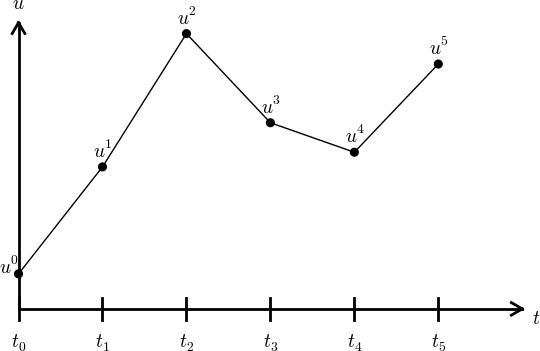
\( u^n \) is a mesh function, defined at the mesh points \( t_n \), \( n=0,\ldots,N_t \) only.
What about a mesh function between the mesh points?
Can extend the mesh function to yield values between mesh points by linear interpolation:
$$
\begin{equation}
u(t) \approx u^n + \frac{u^{n+1}-u^n}{t_{n+1}-t_n}(t - t_n)
\end{equation}
$$

Step 2: Fulfilling the equation at discrete time points
- The ODE holds for all \( t\in (0,T] \) (infinite no of points)
- Idea: let the ODE be valid at the mesh points only (finite no of points)
$$
\begin{equation}
u'(t_n) = -au(t_n),\quad n=1,\ldots,N_t
\tag{3}
\end{equation}
$$
Step 3: Replacing derivatives by finite differences
Now it is time for the finite difference approximations of derivatives:
$$
\begin{equation}
u'(t_n) \approx \frac{u^{n+1}-u^{n}}{t_{n+1}-t_n}
\tag{4}
\end{equation}
$$
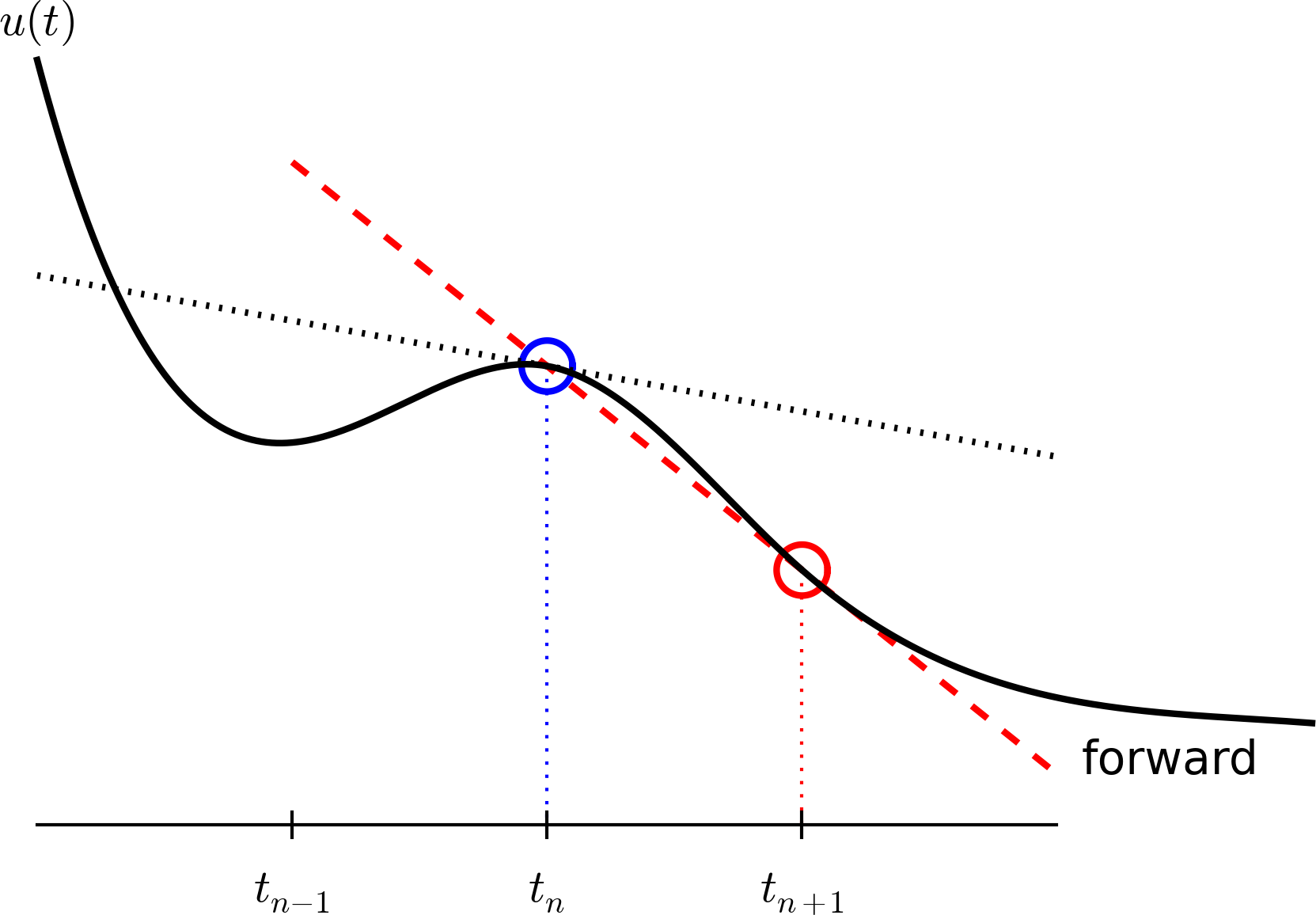
Step 3: Replacing derivatives by finite differences
Inserting the finite difference approximation in
$$ u'(t_n) = -au(t_n)$$
gives
$$
\begin{equation}
\frac{u^{n+1}-u^{n}}{t_{n+1}-t_n} = -au^{n},\quad n=0,1,\ldots,N_t-1
\tag{5}
\end{equation}
$$
(Known as discrete equation, or discrete problem, or finite difference method/scheme)
Step 4: Formulating a recursive algorithm
How can we actually compute the \( u^n \) values?
- given \( u^0=I \)
- compute \( u^1 \) from \( u^0 \)
- compute \( u^2 \) from \( u^1 \)
- compute \( u^3 \) from \( u^2 \) (and so forth)
In general: we have \( u^n \) and seek \( u^{n+1} \)
Solve wrt \( u^{n+1} \) to get the computational formula:
$$
\begin{equation}
u^{n+1} = u^n - a(t_{n+1} -t_n)u^n
\tag{6}
\end{equation}
$$
Let us apply the scheme by hand
Assume constant time spacing: \( \Delta t = t_{n+1}-t_n=\mbox{const} \)
$$
\begin{align*}
u_0 &= I,\\
u_1 & = u^0 - a\Delta t u^0 = I(1-a\Delta t),\\
u_2 & = I(1-a\Delta t)^2,\\
u^3 &= I(1-a\Delta t)^3,\\
&\vdots\\
u^{N_t} &= I(1-a\Delta t)^{N_t}
\end{align*}
$$
Ooops - we can find the numerical solution by hand (in this simple example)! No need for a computer (yet)...
A backward difference
Here is another finite difference approximation to the derivative (backward difference):
$$
\begin{equation}
u'(t_n) \approx \frac{u^{n}-u^{n-1}}{t_{n}-t_{n-1}}
\tag{7}
\end{equation}
$$
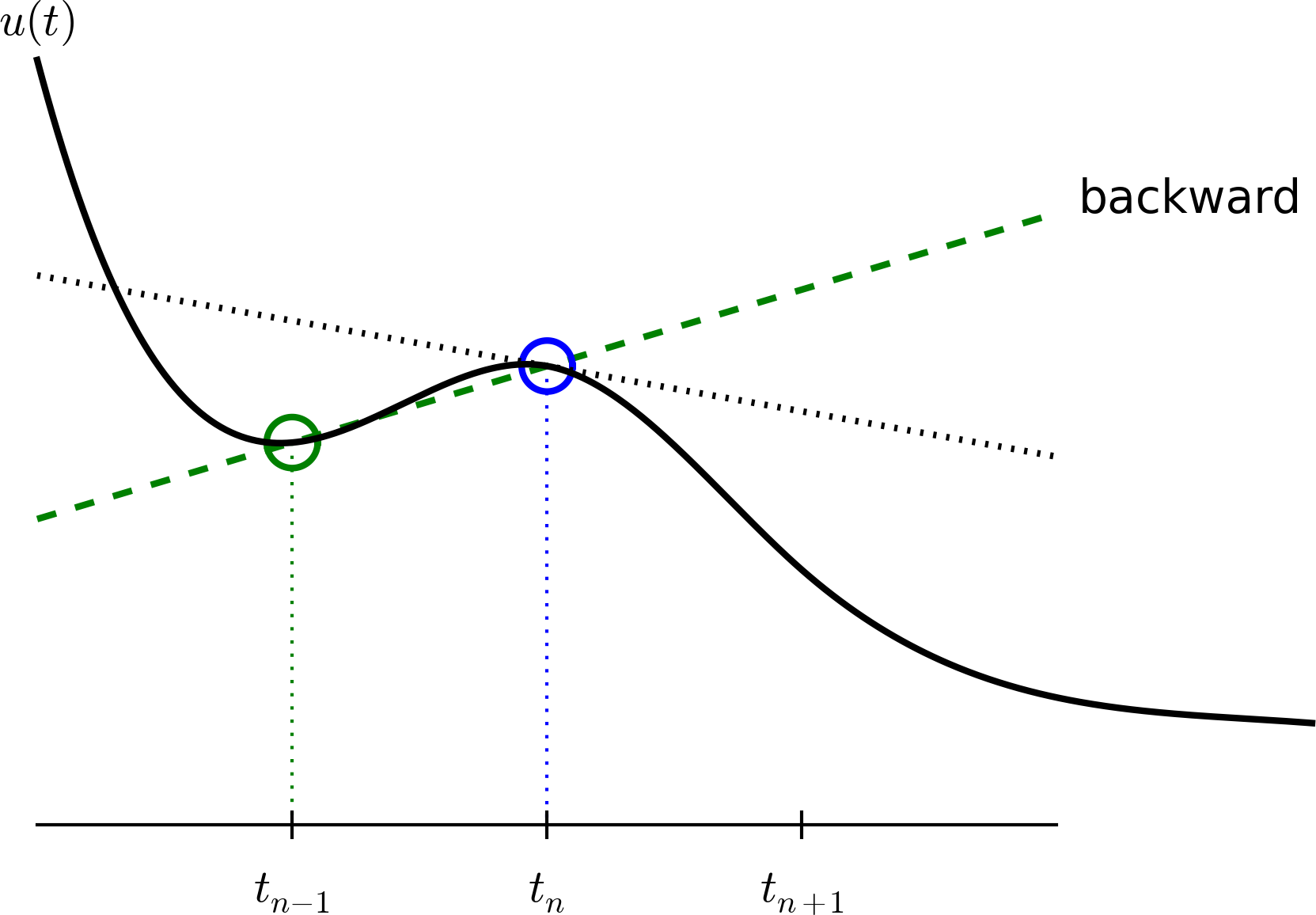
The Backward Euler scheme
Inserting the finite difference approximation in \( u'(t_n)=-au(t_n) \) yields the Backward Euler (BE) scheme:
$$
\begin{equation}
\frac{u^{n}-u^{n-1}}{t_{n}-t_{n-1}} = -a u^n
\tag{8}
\end{equation}
$$
Solve with respect to the unknown \( u^{n+1} \):
$$
\begin{equation}
u^{n+1} = \frac{1}{1+ a(t_{n+1}-t_n)} u^n
\tag{9}
\end{equation}
$$
A centered difference
Centered differences are better approximations than forward or backward differences.
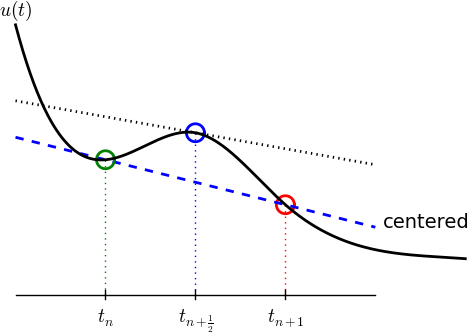
The Crank-Nicolson scheme; ideas
Idea 1: let the ODE hold at \( t_{n+\half} \)
$$ u'(t_{n+\half}) = -au(t_{n+\half})$$
Idea 2: approximate \( u'(t_{n+\half} \) by a centered difference
$$
\begin{equation}
u'(t_{n+\half}) \approx \frac{u^{n+1}-u^n}{t_{n+1}-t_n}
\tag{10}
\end{equation}
$$
Problem: \( u(t_{n+\half}) \) is not defined, only \( u^n=u(t_n) \) and \( u^{n+1}=u(t_{n+1}) \)
Solution:
$$ u(t_{n+\half}) \approx \half(u^n + u^{n+1}) $$
The Crank-Nicolson scheme; result
Result:
$$
\begin{equation}
\frac{u^{n+1}-u^n}{t_{n+1}-t_n} = -a\half (u^n + u^{n+1})
\tag{11}
\end{equation}
$$
Solve wrt to \( u^{n+1} \):
$$
\begin{equation}
u^{n+1} = \frac{1-\half a(t_{n+1}-t_n)}{1 + \half a(t_{n+1}-t_n)}u^n
\tag{12}
\end{equation}
$$
This is a Crank-Nicolson (CN) scheme or a midpoint or centered scheme.
The unifying \( \theta \)-rule
The Forward Euler, Backward Euler, and Crank-Nicolson schemes can be formulated as one scheme with a varying parameter \( \theta \):
$$
\begin{equation}
\frac{u^{n+1}-u^{n}}{t_{n+1}-t_n} = -a (\theta u^{n+1} + (1-\theta) u^{n})
\tag{13}
\end{equation}
$$
- \( \theta =0 \): Forward Euler
- \( \theta =1 \): Backward Euler
- \( \theta =1/2 \): Crank-Nicolson
- We may alternatively choose any \( \theta\in [0,1] \).
\( u^n \) is known, solve for \( u^{n+1} \):
$$
\begin{equation}
u^{n+1} = \frac{1 - (1-\theta) a(t_{n+1}-t_n)}{1 + \theta a(t_{n+1}-t_n)}
\tag{14}
\end{equation}
$$
Constant time step
Very common assumption (not important, but exclusively used for simplicity hereafter): constant time step \( t_{n+1}-t_n\equiv\Delta t \)
$$
\begin{align}
u^{n+1} &= (1 - a\Delta t )u^n \quad (\hbox{FE})
\tag{15}\\
u^{n+1} &= \frac{1}{1+ a\Delta t} u^n \quad (\hbox{BE})
\tag{16}\\
u^{n+1} &= \frac{1-\half a\Delta t}{1 + \half a\Delta t} u^n \quad (\hbox{CN})
\tag{17}\\
u^{n+1} &= \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n \quad (\theta-\hbox{rule})
\tag{18}
\end{align}
$$
Test the understanding!
Derive Forward Euler, Backward Euler, and Crank-Nicolson schemes for Newton's law of cooling:
$$ T' = -k(T-T_s),\quad T(0)=T_0,\ t\in (0,t_{\mbox{end}}]$$
Physical quantities:
- \( T(t) \): temperature of an object at time \( t \)
- \( k \): parameter expressing heat loss to the surroundings
- \( T_s \): temperature of the surroundings
- \( T_0 \): initial temperature
Compact operator notation for finite differences
- Finite difference formulas can be tedious to write and read/understand
- Handy tool: finite difference operator notation
- Advantage: communicates the nature of the difference in a compact way
$$
\begin{equation}
[D_t^- u = -au]^n
\end{equation}
$$
Specific notation for difference operators
Forward difference:
$$
\begin{equation}
[D_t^+u]^n = \frac{u^{n+1} - u^{n}}{\Delta t}
\approx \frac{d}{dt} u(t_n) \tag{19}
\end{equation}
$$
Centered difference:
$$
\begin{equation}
[D_tu]^n = \frac{u^{n+\half} - u^{n-\half}}{\Delta t}
\approx \frac{d}{dt} u(t_n), \tag{20}
\end{equation}
$$
Backward difference:
$$
\begin{equation}
[D_t^-u]^n = \frac{u^{n} - u^{n-1}}{\Delta t}
\approx \frac{d}{dt} u(t_n) \tag{21}
\end{equation}
$$
The Backward Euler scheme with operator notation
$$
\begin{equation*}
[D_t^-u]^n = -au^n
\end{equation*}
$$
Common to put the whole equation inside square brackets:
$$
\begin{equation}
[D_t^- u = -au]^n
\end{equation}
$$
The Forward Euler scheme with operator notation
$$
\begin{equation}
[D_t^+ u = -au]^n
\end{equation}
$$
The Crank-Nicolson scheme with operator notation
Introduce an averaging operator:
$$
\begin{equation}
[\overline{u}^{t}]^n = \half (u^{n-\half} + u^{n+\half} )
\approx u(t_n) \tag{22}
\end{equation}
$$
The Crank-Nicolson scheme can then be written as
$$
\begin{equation}
[D_t u = -a\overline{u}^t]^{n+\half}
\tag{23}
\end{equation}
$$
Test: use the definitions and write out the above formula to see that it really is the Crank-Nicolson scheme!
Implementation
Model:
$$
u'(t) = -au(t),\quad t\in (0,T], \quad u(0)=I
$$
Numerical method:
$$
u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n
$$
for \( \theta\in [0,1] \). Note
- \( \theta=0 \) gives Forward Euler
- \( \theta=1 \) gives Backward Euler
- \( \theta=1/2 \) gives Crank-Nicolson
Requirements of a program
- Compute the numerical solution \( u^n \), \( n=1,2,\ldots,N_t \)
- Display the numerical and exact solution \( \uex(t)=e^{-at} \)
- Bring evidence to a correct implementation (verification)
- Compare the numerical and the exact solution in a plot
- computes the error \( \uex (t_n) - u^n \)
- computes the convergence rate of the numerical scheme
- reads its input data from the command line
Tools to learn
- Basic Python programming
- Array computing with numpy
- Plotting with matplotlib.pyplot and scitools
- File writing and reading
All programs are in the directory src/decay.
Why implement in Python?
- Python has a very clean, readable syntax (often known as "executable pseudo-code").
- Python code is very similar to MATLAB code (and MATLAB has a particularly widespread use for scientific computing).
- Python is a full-fledged, very powerful programming language.
- Python is similar to, but much simpler to work with and results in more reliable code than C++.
Why implement in Python?
- Python has a rich set of modules for scientific computing, and its popularity in scientific computing is rapidly growing.
- Python was made for being combined with compiled languages (C, C++, Fortran) to reuse existing numerical software and to reach high computational performance of new implementations.
- Python has extensive support for administrative task needed when doing large-scale computational investigations.
- Python has extensive support for graphics (visualization, user interfaces, web applications).
- FEniCS, a very powerful tool for solving PDEs by the finite element method, is most human-efficient to operate from Python.
Algorithm
- Store \( u^n \), \( n=0,1,\ldots,N_t \) in an array
u. - Algorithm:
- initialize \( u^0 \)
- for \( t=t_n \), \( n=1,2,\ldots,N_t \): compute \( u_n \) using the \( \theta \)-rule formula
Translation to Python function
from numpy import *
def solver(I, a, T, dt, theta):
"""Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
Nt = int(T/dt) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
return u, t
Note about the for loop: range(0, Nt, s) generates all integers
from 0 to Nt in steps of s (default 1), but not including Nt (!).
Sample call:
u, t = solver(I=1, a=2, T=8, dt=0.8, theta=1)
Integer division
Python applies integer division: 1/2 is 0, while 1./2 or 1.0/2 or
1/2. or 1/2.0 or 1.0/2.0 all give 0.5.
A safer solver function (dt = float(dt) - guarantee float):
from numpy import *
def solver(I, a, T, dt, theta):
"""Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt."""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u[n]
return u, t
Doc strings
- First string after the function heading
- Used for documenting the function
- Automatic documentation tools can make fancy manuals for you
- Can be used for automatic testing
def solver(I, a, T, dt, theta):
"""
Solve
u'(t) = -a*u(t),
with initial condition u(0)=I, for t in the time interval
(0,T]. The time interval is divided into time steps of
length dt.
theta=1 corresponds to the Backward Euler scheme, theta=0
to the Forward Euler scheme, and theta=0.5 to the Crank-
Nicolson method.
"""
...
Formatting of numbers
Can control formatting of reals and integers through the printf format:
print 't=%6.3f u=%g' % (t[i], u[i])
Or the alternative format string syntax:
print 't={t:6.3f} u={u:g}'.format(t=t[i], u=u[i])
Running the program
How to run the program decay_v1.py:
Terminal> python decay_v1.py
Can also run it as "normal" Unix programs: ./decay_v1.py if the
first line is
`#!/usr/bin/env python`
Then
Terminal> chmod a+rx decay_v1.py
Terminal> ./decay_v1.py
Plotting the solution
Basic syntax:
from matplotlib.pyplot import *
plot(t, u)
show()
Can (and should!) add labels on axes, title, legends.
Comparing with the exact solution
Python function for the exact solution \( \uex(t)=Ie^{-at} \):
def exact_solution(t, I, a):
return I*exp(-a*t)
Quick plotting:
u_e = exact_solution(t, I, a)
plot(t, u, t, u_e)
Problem: \( \uex(t) \) applies the same mesh as \( u^n \) and looks as a piecewise linear function.
Remedy: Introduce a very fine mesh for \( \uex \).
t_e = linspace(0, T, 1001) # fine mesh
u_e = exact_solution(t_e, I, a)
plot(t_e, u_e, 'b-', # blue line for u_e
t, u, 'r--o') # red dashes w/circles
Add legends, axes labels, title, and wrap in a function
from matplotlib.pyplot import *
def plot_numerical_and_exact(theta, I, a, T, dt):
"""Compare the numerical and exact solution in a plot."""
u, t = solver(I=I, a=a, T=T, dt=dt, theta=theta)
t_e = linspace(0, T, 1001) # fine mesh for u_e
u_e = exact_solution(t_e, I, a)
plot(t, u, 'r--o', # red dashes w/circles
t_e, u_e, 'b-') # blue line for exact sol.
legend(['numerical', 'exact'])
xlabel('t')
ylabel('u')
title('theta=%g, dt=%g' % (theta, dt))
savefig('plot_%s_%g.png' % (theta, dt))
Complete code in decay_v2.py
Plotting with SciTools
SciTools provides a unified plotting interface (Easyviz) to many different plotting packages: Matplotlib, Gnuplot, Grace, VTK, OpenDX, ...
Can use Matplotlib (MATLAB-like) syntax,
or a more compact plot function syntax:
from scitools.std import *
plot(t, u, 'r--o', # red dashes w/circles
t_e, u_e, 'b-', # blue line for exact sol.
legend=['numerical', 'exact'],
xlabel='t',
ylabel='u',
title='theta=%g, dt=%g' % (theta, dt),
savefig='%s_%g.png' % (theta2name[theta], dt),
show=True)
Change backend (plotting engine, Matplotlib by default):
Terminal> python decay_plot_st.py --SCITOOLS_easyviz_backend gnuplot
Terminal> python decay_plot_st.py --SCITOOLS_easyviz_backend grace
Verifying the implementation
- Verification = bring evidence that the program works
- Find suitable test problems
- Make function for each test problem
- Later: put the verification tests in a professional testing framework
Simplest method: run a few algorithmic steps by hand
Use a calculator (\( I=0.1 \), \( \theta=0.8 \), \( \Delta t =0.8 \)):
$$ A\equiv \frac{1 - (1-\theta) a\Delta t}{1 + \theta a \Delta t} = 0.298245614035$$
$$
\begin{align*}
u^1 &= AI=0.0298245614035,\\
u^2 &= Au^1= 0.00889504462912,\\
u^3 &=Au^2= 0.00265290804728
\end{align*}
$$
See the function verify_three_steps in decay_verf1.py.
Comparison with an exact discrete solution
Compare computed numerical solution with a closed-form exact discrete solution (if possible).
Define
$$ A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a \Delta t}$$
Repeated use of the \( \theta \)-rule:
$$
\begin{align*}
u^0 &= I,\\
u^1 &= Au^0 = AI\\
u^n &= A^nu^{n-1} = A^nI
\end{align*}
$$
Making a test based on an exact discrete solution
The exact discrete solution is
$$
\begin{equation}
u^n = IA^n
\tag{24}
\end{equation}
$$
Understand what \( n \) in \( u^n \) and in \( A^n \) means!
Test if
$$ \max_n |u^n - \uex(t_n)| < \epsilon\sim 10^{-15}$$
Implementation in decay_verf2.py.
Test the understanding!
Make a program for solving Newton's law of cooling
$$ T' = -k(T-T_s),\quad T(0)=T_0,\ t\in (0,t_{\mbox{end}}]$$
with the Forward Euler, Backward Euler, and Crank-Nicolson schemes
(or a \( \theta \) scheme). Verify the implementation.
Computing the numerical error as a mesh function
Task: compute the numerical error \( e^n = \uex(t_n) - u^n \)
Exact solution: \( \uex(t)=Ie^{-at} \), implemented as
def exact_solution(t, I, a):
return I*exp(-a*t)
Compute \( e^n \) by
u, t = solver(I, a, T, dt, theta) # Numerical solution
u_e = exact_solution(t, I, a)
e = u_e - u
-
exact_solution(t, I, a)works withtas array - Must have
expfromnumpy(notmath) -
e = u_e - u: array subtraction - Array arithmetics gives shorter and much faster code
Computing the norm of the error
- \( e^n \) is a mesh function
- Usually we want one number for the error
- Use a norm of \( e^n \)
Norms of a function \( f(t) \):
$$
\begin{align}
||f||_{L^2} &= \left( \int_0^T f(t)^2 dt\right)^{1/2}
\tag{25}\\
||f||_{L^1} &= \int_0^T |f(t)| dt
\tag{26}\\
||f||_{L^\infty} &= \max_{t\in [0,T]}|f(t)|
\tag{27}
\end{align}
$$
Norms of mesh functions
- Problem: \( f^n =f(t_n) \) is a mesh function and hence not defined for all \( t \). How to integrate \( f^n \)?
- Idea: Apply a numerical integration rule, using only the mesh points of the mesh function.
The Trapezoidal rule:
$$ ||f^n|| = \left(\Delta t\left(\half(f^0)^2 + \half(f^{N_t})^2
+ \sum_{n=1}^{N_t-1} (f^n)^2\right)\right)^{1/2} $$
Common simplification yields the \( L^2 \) norm of a mesh function:
$$ ||f^n||_{\ell^2} = \left(\Delta t\sum_{n=0}^{N_t} (f^n)^2\right)^{1/2}$$
Implementation of the norm of the error
$$ E = ||e^n||_{\ell^2} = \sqrt{\Delta t\sum_{n=0}^{N_t} (e^n)^2}$$
Python w/array arithmetics:
e = exact_solution(t) - u
E = sqrt(dt*sum(e**2))
Comment on array vs scalar computation
Scalar computing of E = sqrt(dt*sum(e**2)):
m = len(u) # length of u array (alt: u.size)
u_e = zeros(m)
t = 0
for i in range(m):
u_e[i] = exact_solution(t, a, I)
t = t + dt
e = zeros(m)
for i in range(m):
e[i] = u_e[i] - u[i]
s = 0 # summation variable
for i in range(m):
s = s + e[i]**2
error = sqrt(dt*s)
Obviously, scalar computing
- takes more code
- is less readable
- runs much slower
Compute on entire arrays (when possible)!
Memory-saving implementation
- Note 1: we store the entire array
u, i.e., \( u^n \) for \( n=0,1,\ldots,N_t \) - Note 2: the formula for \( u^{n+1} \) needs \( u^n \) only, not \( u^{n-1} \), \( u^{n-2} \), ...
- No need to store more than \( u^{n+1} \) and \( u^{n} \)
- Extremely important when solving PDEs
- No practical importance here (much memory available)
- But let's illustrate how to do save memory!
- Idea 1: store \( u^{n+1} \) in
u, \( u^n \) inu_1(float) - Idea 2: store
uin a file, read file later for plotting
Memory-saving solver function
def solver_memsave(I, a, T, dt, theta, filename='sol.dat'):
"""
Solve u'=-a*u, u(0)=I, for t in (0,T] with steps of dt.
Minimum use of memory. The solution is stored in a file
(with name filename) for later plotting.
"""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of intervals
outfile = open(filename, 'w')
# u: time level n+1, u_1: time level n
t = 0
u_1 = I
outfile.write('%.16E %.16E\n' % (t, u_1))
for n in range(1, Nt+1):
u = (1 - (1-theta)*a*dt)/(1 + theta*dt*a)*u_1
u_1 = u
t += dt
outfile.write('%.16E %.16E\n' % (t, u))
outfile.close()
return u, t
Reading computed data from file
def read_file(filename='sol.dat'):
infile = open(filename, 'r')
u = []; t = []
for line in infile:
words = line.split()
if len(words) != 2:
print 'Found more than two numbers on a line!', words
sys.exit(1) # abort
t.append(float(words[0]))
u.append(float(words[1]))
return np.array(t), np.array(u)
Simpler code with numpy functionality for reading/writing tabular data:
def read_file_numpy(filename='sol.dat'):
data = np.loadtxt(filename)
t = data[:,0]
u = data[:,1]
return t, u
Similar function np.savetxt, but then we need all \( u^n \) and \( t^n \) values
in a two-dimensional array (which we try to prevent now!).
Usage of memory-saving code
def explore(I, a, T, dt, theta=0.5, makeplot=True):
filename = 'u.dat'
u, t = solver_memsave(I, a, T, dt, theta, filename)
t, u = read_file(filename)
u_e = exact_solution(t, I, a)
e = u_e - u
E = np.sqrt(dt*np.sum(e**2))
if makeplot:
plt.figure()
...
Complete program: decay_memsave.py.
Analysis of finite difference equations
Model:
$$
\begin{equation}
u'(t) = -au(t),\quad u(0)=I
\end{equation}
$$
Method:
$$
\begin{equation}
u^{n+1} = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}u^n
\tag{28}
\end{equation}
$$
How good is this method? Is it safe to use it?
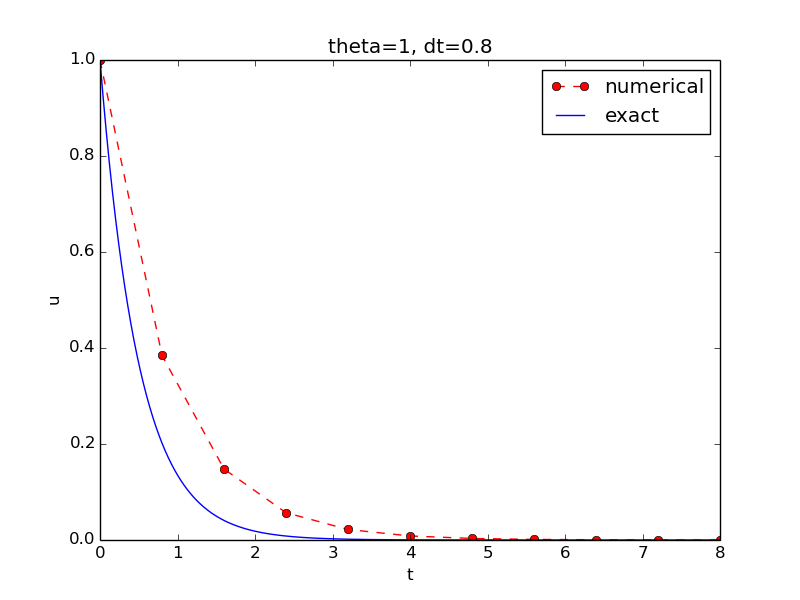
Encouraging numerical solutions
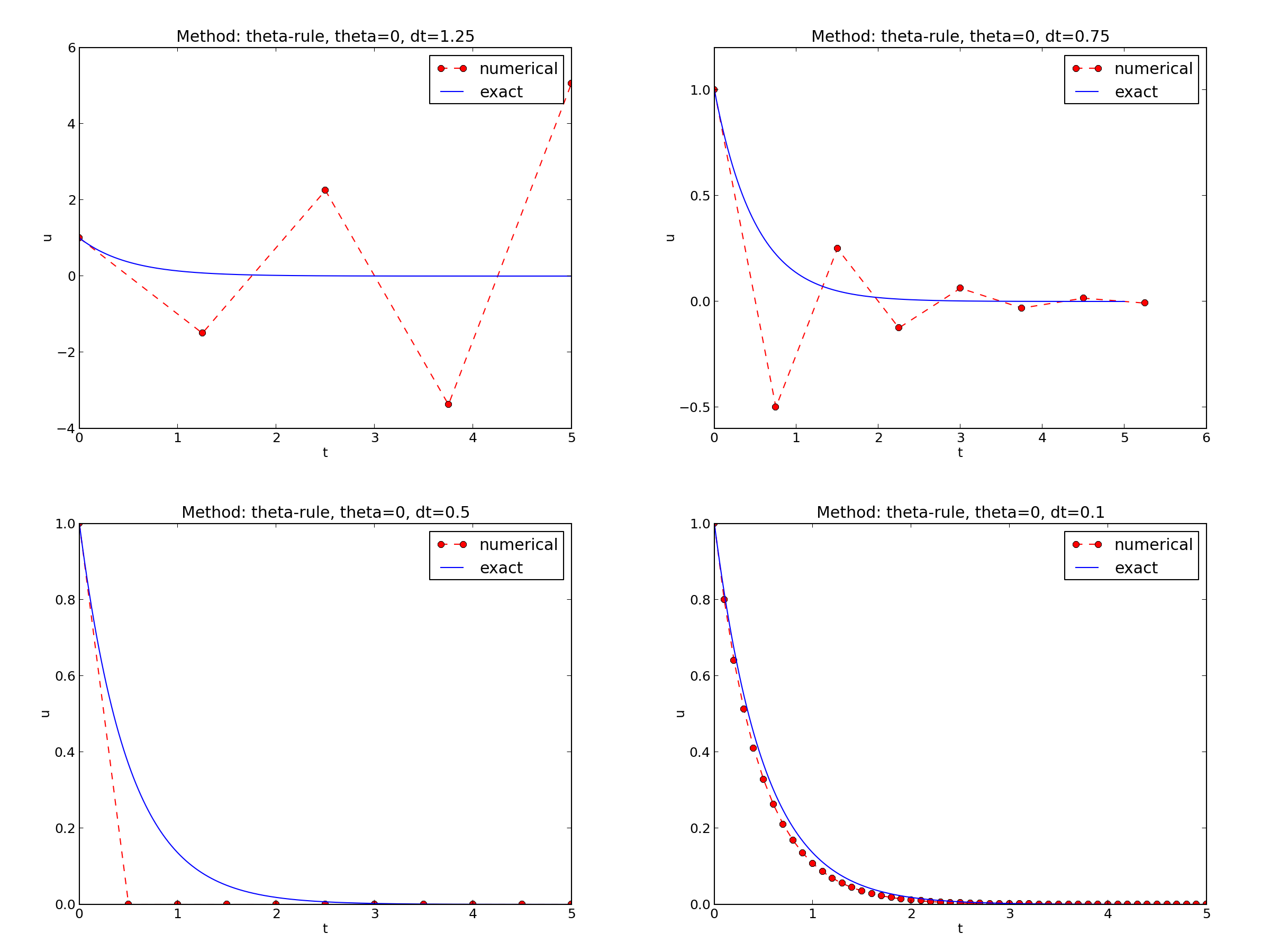
\( I=1 \), \( a=2 \), \( \theta =1,0.5, 0 \), \( \Delta t=1.25, 0.75, 0.5, 0.1 \).
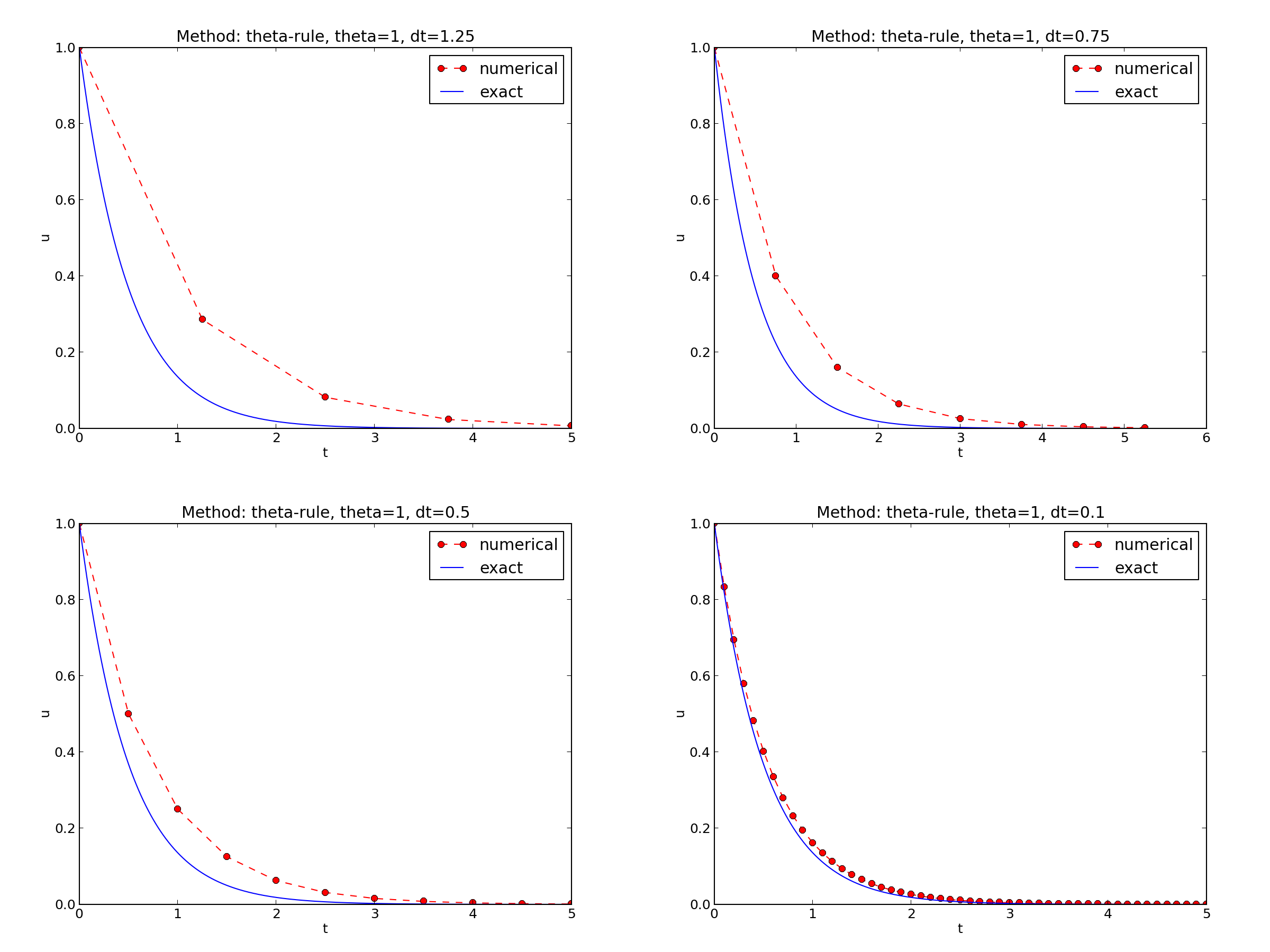
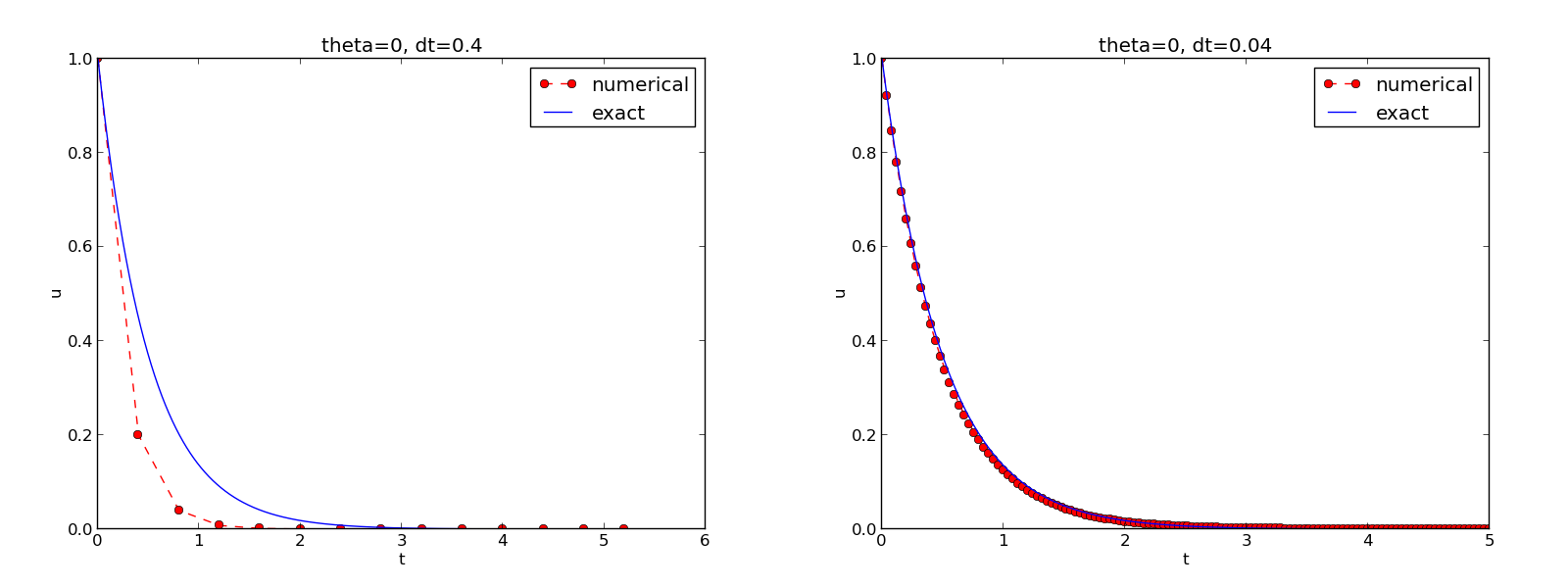
Discouraging numerical solutions; Crank-Nicolson
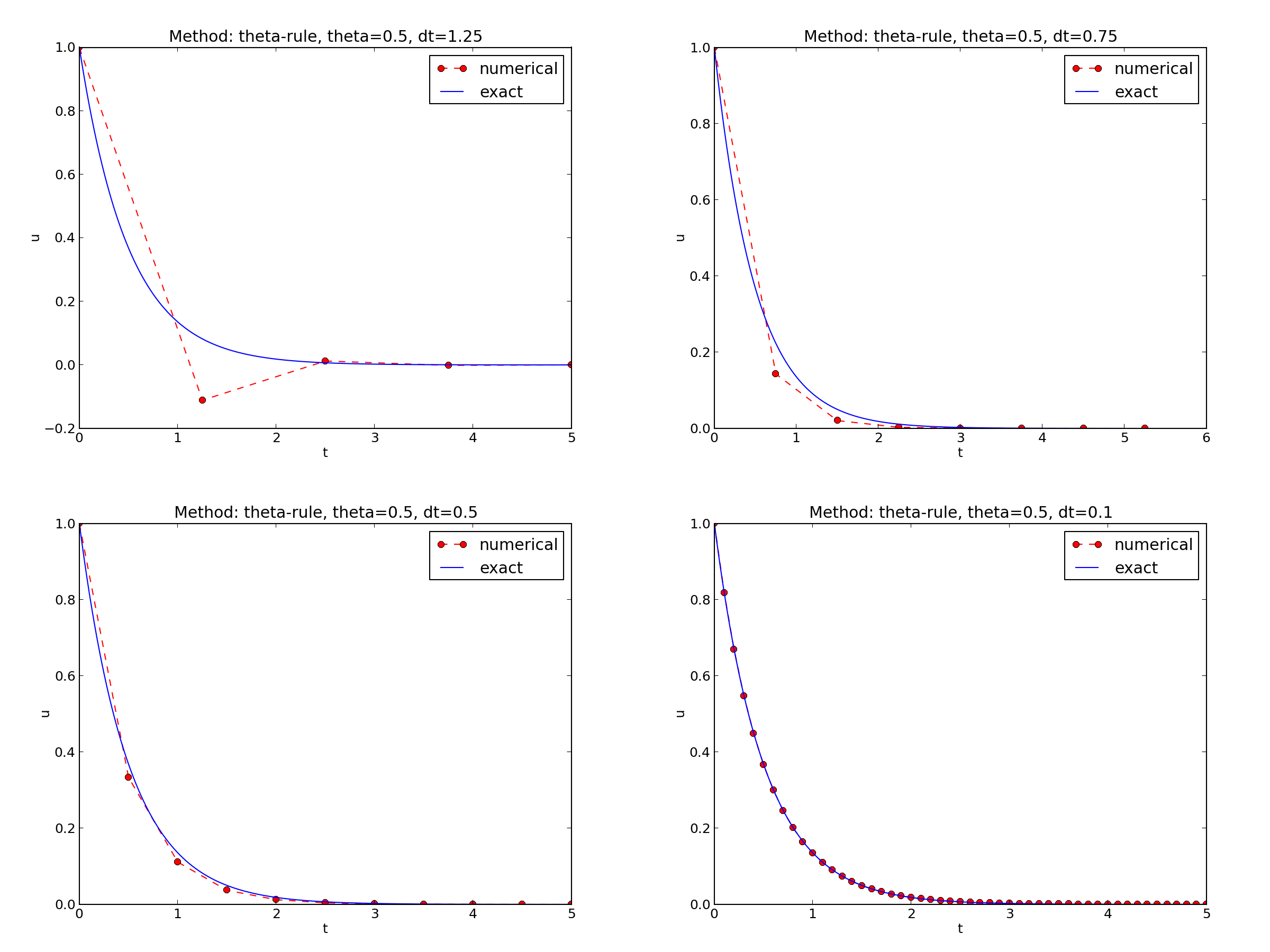
Discouraging numerical solutions; Forward Euler
Summary of observations
The characteristics of the displayed curves can be summarized as follows:
- The Backward Euler scheme always gives a monotone solution, lying above the exact curve.
- The Crank-Nicolson scheme gives the most accurate results, but for \( \Delta t=1.25 \) the solution oscillates.
- The Forward Euler scheme gives a growing, oscillating solution for \( \Delta t=1.25 \); a decaying, oscillating solution for \( \Delta t=0.75 \); a strange solution \( u^n=0 \) for \( n\geq 1 \) when \( \Delta t=0.5 \); and a solution seemingly as accurate as the one by the Backward Euler scheme for \( \Delta t = 0.1 \), but the curve lies below the exact solution.
Problem setting
We ask the question
- Under what circumstances, i.e., values of the input data \( I \), \( a \), and \( \Delta t \) will the Forward Euler and Crank-Nicolson schemes result in undesired oscillatory solutions?
Techniques of investigation:
- Numerical experiments
- Mathematical analysis
Another question to be raised is
- How does \( \Delta t \) impact the error in the numerical solution?
Experimental investigation of oscillatory solutions
The solution is oscillatory if
$$ u^{n} > u^{n-1}$$
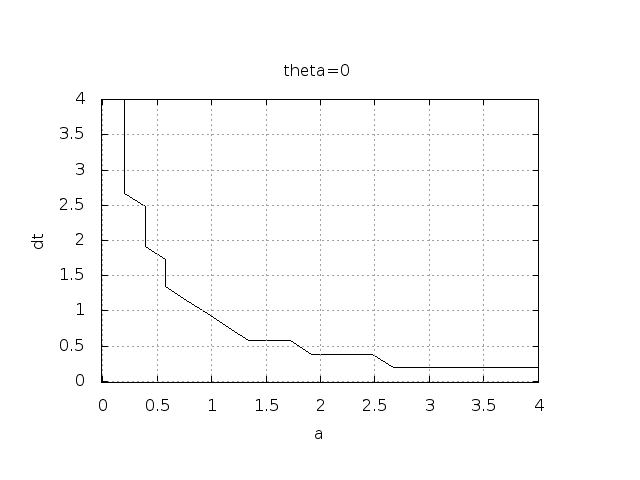
Seems that \( a\Delta t < 1 \) for FE and 2 for CN.
Exact numerical solution
Starting with \( u^0=I \), the simple recursion (28) can be applied repeatedly \( n \) times, with the result that
$$
\begin{equation}
u^{n} = IA^n,\quad A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t}
\tag{29}
\end{equation}
$$
Such an exact discrete solution is unusual, but very handy for analysis.
Stability
Since \( u^n\sim A^n \),
- \( A < 0 \) gives a factor \( (-1)^n \) and oscillatory solutions
- \( |A|>1 \) gives growing solutions
- Recall: the exact solution is monotone and decaying
- If these qualitative properties are not met, we say that the numerical solution is unstable
Computation of stability in this problem
\( A < 0 \) if
$$
\frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} < 0
$$
To avoid oscillatory solutions we must have \( A> 0 \) and
$$
\begin{equation}
\Delta t < \frac{1}{(1-\theta)a}\
\end{equation}
$$
- Always fulfilled for Backward Euler
- \( \Delta t \leq 1/a \) for Forward Euler
- \( \Delta t \leq 2/a \) for Crank-Nicolson
Computation of stability in this problem
\( |A|\leq 1 \) means \( -1\leq A\leq 1 \)
$$
\begin{equation}
-1\leq\frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} \leq 1
\tag{30}
\end{equation}
$$
\( -1 \) is the critical limit:
$$
\begin{align*}
\Delta t &\leq \frac{2}{(1-2\theta)a},\quad \theta < \half\\
\Delta t &\geq \frac{2}{(1-2\theta)a},\quad \theta > {\half}
\end{align*}
$$
- Always fulfilled for Backward Euler and Crank-Nicolson
- \( \Delta t \leq 2/a \) for Forward Euler
Explanation of problems with Forward Euler

- \( a\Delta t= 2\cdot 1.25=2.5 \) and \( A=-1.5 \): oscillations and growth
- \( a\Delta t = 2\cdot 0.75=1.5 \) and \( A=-0.5 \): oscillations and decay
- \( \Delta t=0.5 \) and \( A=0 \): \( u^n=0 \) for \( n>0 \)
- Smaller \( Delta t \): qualitatively correct solution
Explanation of problems with Crank-Nicolson

- \( \Delta t=1.25 \) and \( A=-0.25 \): oscillatory solution
- Never any growing solution
Summary of stability
- Forward Euler is conditionally stable
- \( \Delta t < 2/a \) for avoiding growth
- \( \Delta t\leq 1/a \) for avoiding oscillations
- The Crank-Nicolson is unconditionally stable wrt growth and conditionally stable wrt oscillations
- \( \Delta t < 2/a \) for avoiding oscillations
- Backward Euler is unconditionally stable
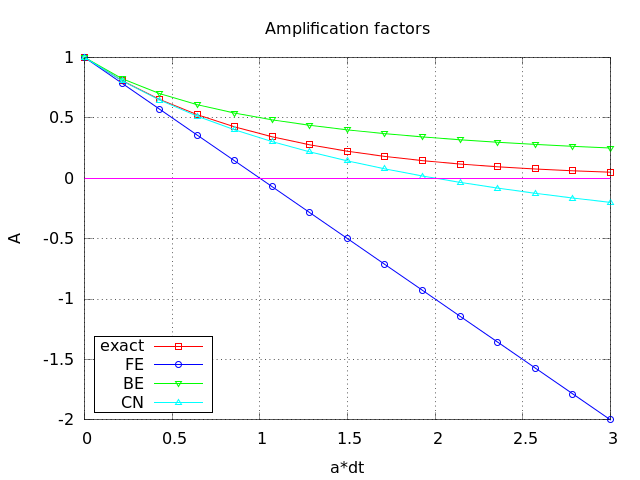
Comparing amplification factors
\( u^{n+1} \) is an amplification \( A \) of \( u^n \):
$$ u^{n+1} = Au^n,\quad A = \frac{1 - (1-\theta) a\Delta t}{1 + \theta a\Delta t} $$
The exact solution is also an amplification:
$$ u(t_{n+1}) = \Aex u(t_n), \quad \Aex = e^{-a\Delta t}$$
A possible measure of accuracy: \( \Aex - A \)
Plot of amplification factors
Series expansion of amplification factors
To investigate \( \Aex - A \) mathematically, we can Taylor expand the expression, using \( p=a\Delta t \) as variable.
>>> from sympy import *
>>> # Create p as a mathematical symbol with name 'p'
>>> p = Symbol('p')
>>> # Create a mathematical expression with p
>>> A_e = exp(-p)
>>>
>>> # Find the first 6 terms of the Taylor series of A_e
>>> A_e.series(p, 0, 6)
1 + (1/2)*p**2 - p - 1/6*p**3 - 1/120*p**5 + (1/24)*p**4 + O(p**6)
>>> theta = Symbol('theta')
>>> A = (1-(1-theta)*p)/(1+theta*p)
>>> FE = A_e.series(p, 0, 4) - A.subs(theta, 0).series(p, 0, 4)
>>> BE = A_e.series(p, 0, 4) - A.subs(theta, 1).series(p, 0, 4)
>>> half = Rational(1,2) # exact fraction 1/2
>>> CN = A_e.series(p, 0, 4) - A.subs(theta, half).series(p, 0, 4)
>>> FE
(1/2)*p**2 - 1/6*p**3 + O(p**4)
>>> BE
-1/2*p**2 + (5/6)*p**3 + O(p**4)
>>> CN
(1/12)*p**3 + O(p**4)
Error in amplification factors
Focus: the error measure \( A-\Aex \) as function of \( \Delta t \) (recall that \( p=a\Delta t \)):
$$
\begin{equation}
A-\Aex = \left\lbrace\begin{array}{ll}
\Oof{\Delta t^2}, & \hbox{Forward and Backward Euler},\\
\Oof{\Delta t^3}, & \hbox{Crank-Nicolson}
\end{array}\right.
\end{equation}
$$
The fraction of numerical and exact amplification factors
Focus: the error measure \( 1-A/\Aex \) as function of \( p=a\Delta t \):
>>> FE = 1 - (A.subs(theta, 0)/A_e).series(p, 0, 4)
>>> BE = 1 - (A.subs(theta, 1)/A_e).series(p, 0, 4)
>>> CN = 1 - (A.subs(theta, half)/A_e).series(p, 0, 4)
>>> FE
(1/2)*p**2 + (1/3)*p**3 + O(p**4)
>>> BE
-1/2*p**2 + (1/3)*p**3 + O(p**4)
>>> CN
(1/12)*p**3 + O(p**4)
Same leading-order terms as for the error measure \( A-\Aex \).
The true/global error at a point
- The error in \( A \) reflects the local error when going from one time step to the next
- What is the global (true) error at \( t_n \)? \( e^n = \uex(t_n) - u^n = Ie^{-at_n} - IA^n \)
- Taylor series expansions of \( e^n \) simplify the expression
Computing the global error at a point
>>> n = Symbol('n')
>>> u_e = exp(-p*n) # I=1
>>> u_n = A**n # I=1
>>> FE = u_e.series(p, 0, 4) - u_n.subs(theta, 0).series(p, 0, 4)
>>> BE = u_e.series(p, 0, 4) - u_n.subs(theta, 1).series(p, 0, 4)
>>> CN = u_e.series(p, 0, 4) - u_n.subs(theta, half).series(p, 0, 4)
>>> FE
(1/2)*n*p**2 - 1/2*n**2*p**3 + (1/3)*n*p**3 + O(p**4)
>>> BE
(1/2)*n**2*p**3 - 1/2*n*p**2 + (1/3)*n*p**3 + O(p**4)
>>> CN
(1/12)*n*p**3 + O(p**4)
Substitute \( n \) by \( t/\Delta t \):
- Forward and Backward Euler: leading order term \( \half ta^2\Delta t \)
- Crank-Nicolson: leading order term \( \frac{1}{12}ta^3\Delta t^2 \)
Convergence
The numerical scheme is convergent if the global error \( e^n\rightarrow 0 \) as \( \Delta t\rightarrow 0 \). If the error has a leading order term \( \Delta t^r \), the convergence rate is of order \( r \).
Integrated errors
Focus: norm of the numerical error
$$ ||e^n||_{\ell^2} = \sqrt{\Delta t\sum_{n=0}^{N_t} ({\uex}(t_n) - u^n)^2}$$
Forward and Backward Euler:
$$ ||e^n||_{\ell^2} = \frac{1}{4}\sqrt{\frac{T^3}{3}} a^2\Delta t$$
Crank-Nicolson:
$$ ||e^n||_{\ell^2} = \frac{1}{12}\sqrt{\frac{T^3}{3}}a^3\Delta t^2$$
Analysis of both the pointwise and the time-integrated true errors:
- 1st order for Forward and Backward Euler
- 2nd order for Crank-Nicolson
Truncation error
- How good is the discrete equation?
- Possible answer: see how well \( \uex \) fits the discrete equation
$$ \lbrack D_t u = -au\rbrack^n$$
i.e.,
$$ \frac{u^{n+1}-u^n}{\Delta t} = -au^n$$
Insert \( \uex \) (which does not in general fulfill this equation):
$$
\begin{equation}
\frac{\uex(t_{n+1})-\uex(t_n)}{\Delta t} + a\uex(t_n) = R^n \neq 0
\tag{31}
\end{equation}
$$
Computation of the truncation error
- The residual \( R^n \) is the truncation error.
- How does \( R^n \) vary with \( \Delta t \)?
Tool: Taylor expand \( \uex \) around the point where the ODE is sampled (here \( t_n \))
$$ \uex(t_{n+1}) = \uex(t_n) + \uex'(t_n)\Delta t + \half\uex''(t_n)
\Delta t^2 + \cdots $$
Inserting this Taylor series in (31) gives
$$ R^n = \uex'(t_n) + \half\uex''(t_n)\Delta t + \ldots + a\uex(t_n)$$
Now, \( \uex \) solves the ODE \( \uex'=-a\uex \), and then
$$ R^n \approx \half\uex''(t_n)\Delta t$$
This is a mathematical expression for the truncation error.
The truncation error for other schemes
Backward Euler:
$$ R^n \approx -\half\uex''(t_n)\Delta t $$
Crank-Nicolson:
$$ R^{n+\half} \approx \frac{1}{24}\uex'''(t_{n+\half})\Delta t^2$$
Consistency, stability, and convergence
- Truncation error measures the residual in the difference equations. The scheme is consistent if the truncation error goes to 0 as \( \Delta t\rightarrow 0 \). Importance: the difference equations approaches the differential equation as \( \Delta t\rightarrow 0 \).
- Stability means that the numerical solution exhibits the same qualitative properties as the exact solution. Here: monotone, decaying function.
- Convergence implies that the true (global) error \( e^n =\uex(t_n)-u^n\rightarrow 0 \) as \( \Delta t\rightarrow 0 \). This is really what we want!
The Lax equivalence theorem for linear differential equations: consistency + stability is equivalent with convergence.
(Consistency and stability is in most problems much easier to establish than convergence.)
Model extensions
Extension to a variable coefficient; Forward and Backward Euler
$$
\begin{equation}
u'(t) = -a(t)u(t),\quad t\in (0,T],\quad u(0)=I
\tag{32}
\end{equation}
$$
The Forward Euler scheme:
$$
\begin{equation}
\frac{u^{n+1} - u^n}{\Delta t} = -a(t_n)u^n
\end{equation}
$$
The Backward Euler scheme:
$$
\begin{equation}
\frac{u^{n} - u^{n-1}}{\Delta t} = -a(t_n)u^n
\end{equation}
$$
Extension to a variable coefficient; Crank-Nicolson
Eevaluting \( a(t_{n+\half}) \) and using an average for \( u \):
$$
\begin{equation}
\frac{u^{n+1} - u^{n}}{\Delta t} = -a(t_{n+\half})\half(u^n + u^{n+1})
\end{equation}
$$
Using an average for \( a \) and \( u \):
$$
\begin{equation}
\frac{u^{n+1} - u^{n}}{\Delta t} = -\half(a(t_n)u^n + a(t_{n+1})u^{n+1})
\end{equation}
$$
Extension to a variable coefficient; \( \theta \)-rule
The \( \theta \)-rule unifies the three mentioned schemes,
$$
\begin{equation}
\frac{u^{n+1} - u^{n}}{\Delta t} = -a((1-\theta)t_n + \theta t_{n+1})((1-\theta) u^n + \theta u^{n+1})
\end{equation}
$$
or,
$$
\begin{equation}
\frac{u^{n+1} - u^{n}}{\Delta t} = -(1-\theta) a(t_n)u^n - \theta
a(t_{n+1})u^{n+1}
\end{equation}
$$
Extension to a variable coefficient; operator notation
$$
\begin{align*}
\lbrack D^+_t u &= -au\rbrack^n,\\
\lbrack D^-_t u &= -au\rbrack^n,\\
\lbrack D_t u &= -a\overline{u}^t\rbrack^{n+\half},\\
\lbrack D_t u &= -\overline{au}^t\rbrack^{n+\half}\\
\end{align*}
$$
Extension to a source term
$$
\begin{equation}
u'(t) = -a(t)u(t) + b(t),\quad t\in (0,T],\quad u(0)=I
\tag{33}
\end{equation}
$$
$$
\begin{align*}
\lbrack D^+_t u &= -au + b\rbrack^n,\\
\lbrack D^-_t u &= -au + b\rbrack^n,\\
\lbrack D_t u &= -a\overline{u}^t + b\rbrack^{n+\half},\\
\lbrack D_t u &= \overline{-au+b}^t\rbrack^{n+\half}
\end{align*}
$$
Implementation of the generalized model problem
$$
\begin{equation}
u^{n+1} = ((1 - \Delta t(1-\theta)a^n)u^n
+ \Delta t(\theta b^{n+1} + (1-\theta)b^n))(1 + \Delta t\theta a^{n+1})^{-1}
\end{equation}
$$
Implementation where \( a(t) \) and \( b(t) \) are given as Python functions (see file decay_vc.py):
def solver(I, a, b, T, dt, theta):
"""
Solve u'=-a(t)*u + b(t), u(0)=I,
for t in (0,T] with steps of dt.
a and b are Python functions of t.
"""
dt = float(dt) # avoid integer division
Nt = int(round(T/dt)) # no of time intervals
T = Nt*dt # adjust T to fit time step dt
u = zeros(Nt+1) # array of u[n] values
t = linspace(0, T, Nt+1) # time mesh
u[0] = I # assign initial condition
for n in range(0, Nt): # n=0,1,...,Nt-1
u[n+1] = ((1 - dt*(1-theta)*a(t[n]))*u[n] + \
dt*(theta*b(t[n+1]) + (1-theta)*b(t[n])))/\
(1 + dt*theta*a(t[n+1]))
return u, t
Implementations of variable coefficients; functions
Plain functions:
def a(t):
return a_0 if t < tp else k*a_0
def b(t):
return 1
Implementations of variable coefficients; classes
Better implementation: class with the parameters a0, tp, and k
as attributes and a special method __call__ for evaluating \( a(t) \):
class A:
def __init__(self, a0=1, k=2):
self.a0, self.k = a0, k
def __call__(self, t):
return self.a0 if t < self.tp else self.k*self.a0
a = A(a0=2, k=1) # a behaves as a function a(t)
Implementations of variable coefficients; lambda function
Quick writing: a one-liner lambda function
a = lambda t: a_0 if t < tp else k*a_0
In general,
f = lambda arg1, arg2, ...: expressin
is equivalent to
def f(arg1, arg2, ...):
return expression
One can use lambda functions directly in calls:
u, t = solver(1, lambda t: 1, lambda t: 1, T, dt, theta)
for a problem \( u'=-u+1 \), \( u(0)=1 \).
A lambda function can appear anywhere where a variable can appear.
Verification via trivial solutions
- Start debugging of a new code with trying a problem where \( u=\hbox{const} \neq 0 \).
- Choose \( u=C \) (a constant). Choose any \( a(t) \) and set \( b=a(t)C \) and \( I=C \).
- "All" numerical methods will reproduce \( u=_{\hbox{const}} \) exactly (machine precision).
- Often \( u=C \) eases debugging.
- In this example: any error in the formula for \( u^{n+1} \) make \( u\neq C \)!
Verification via trivial solutions; test function
def test_constant_solution():
"""
Test problem where u=u_const is the exact solution, to be
reproduced (to machine precision) by any relevant method.
"""
def exact_solution(t):
return u_const
def a(t):
return 2.5*(1+t**3) # can be arbitrary
def b(t):
return a(t)*u_const
u_const = 2.15
theta = 0.4; I = u_const; dt = 4
Nt = 4 # enough with a few steps
u, t = solver(I=I, a=a, b=b, T=Nt*dt, dt=dt, theta=theta)
print u
u_e = exact_solution(t)
difference = abs(u_e - u).max() # max deviation
tol = 1E-14
assert difference < tol
Verification via manufactured solutions
- Choose any formula for \( u(t) \).
- Fit \( I \), \( a(t) \), and \( b(t) \) in \( u'=-au+b \), \( u(0)=I \), to make the chosen formula a solution of the ODE problem.
- Then we can always have an analytical solution (!).
- Ideal for verification: testing convergence rates.
- Called the method of manufactured solutions (MMS)
- Special case: \( u \) linear in \( t \), because all sound numerical methods will reproduce a linear \( u \) exactly (machine precision).
- \( u(t) = ct + d \). \( u(0)=0 \) means \( d=I \).
- ODE implies \( c = -a(t)u + b(t) \).
- Choose \( a(t) \) and \( c \), and set \( b(t) = c + a(t)(ct + I) \).
- Any error in the formula for \( u^{n+1} \) makes \( u\neq ct+I \)!
Linear manufactured solution
\( u^n = ct_n+I \) fulfills the discrete equations!
First,
$$
\begin{align}
\lbrack D_t^+ t\rbrack^n &= \frac{t_{n+1}-t_n}{\Delta t}=1,
\tag{34}\\
\lbrack D_t^- t\rbrack^n &= \frac{t_{n}-t_{n-1}}{\Delta t}=1,
\tag{35}\\
\lbrack D_t t\rbrack^n &= \frac{t_{n+\half}-t_{n-\half}}{\Delta t}=\frac{(n+\half)\Delta t - (n-\half)\Delta t}{\Delta t}=1\tag{36}
\end{align}
$$
Forward Euler:
$$ [D^+ u = -au + b]^n $$
\( a^n=a(t_n) \), \( b^n=c + a(t_n)(ct_n + I) \), and \( u^n=ct_n + I \) results in
$$ c = -a(t_n)(ct_n+I) + c + a(t_n)(ct_n + I) = c $$
Test function for linear manufactured solution
def test_linear_solution():
"""
Test problem where u=c*t+I is the exact solution, to be
reproduced (to machine precision) by any relevant method.
"""
def exact_solution(t):
return c*t + I
def a(t):
return t**0.5 # can be arbitrary
def b(t):
return c + a(t)*exact_solution(t)
theta = 0.4; I = 0.1; dt = 0.1; c = -0.5
T = 4
Nt = int(T/dt) # no of steps
u, t = solver(I=I, a=a, b=b, T=Nt*dt, dt=dt, theta=theta)
u_e = exact_solution(t)
difference = abs(u_e - u).max() # max deviation
print difference
tol = 1E-14 # depends on c!
assert difference < tol
Extension to systems of ODEs
Sample system:
$$
\begin{align}
u' &= a u + bv\\
v' &= cu + dv
\end{align}
$$
The Forward Euler method:
$$
\begin{align}
u^{n+1} &= u^n + \Delta t (a u^n + b v^n)\\
v^{n+1} &= u^n + \Delta t (cu^n + dv^n)
\end{align}
$$
The Backward Euler method gives a system of algebraic equations
The Backward Euler scheme:
$$
\begin{align}
u^{n+1} &= u^n + \Delta t (a u^{n+1} + b v^{n+1})\\
v^{n+1} &= v^n + \Delta t (c u^{n+1} + d v^{n+1})
\end{align}
$$
which is a \( 2\times 2 \) linear system:
$$
\begin{align}
(1 - \Delta t a)u^{n+1} + bv^{n+1} &= u^n \\
c u^{n+1} + (1 - \Delta t d) v^{n+1} &= v^n
\end{align}
$$
Crank-Nicolson also gives a \( 2\times 2 \) linear system.
Methods for general first-order ODEs
Generic form
The standard form for ODEs:
$$
\begin{equation}
u' = f(u,t),\quad u(0)=I
\tag{37}
\end{equation}
$$
\( u \) and \( f \): scalar or vector.
Vectors in case of ODE systems:
$$ u(t) = (u^{(0)}(t),u^{(1)}(t),\ldots,u^{(m-1)}(t)) $$
$$
\begin{align*}
f(u, t) = ( & f^{(0)}(u^{(0)},\ldots,u^{(m-1)})\\
& f^{(1)}(u^{(0)},\ldots,u^{(m-1)}),\\
& \vdots\\
& f^{(m-1)}(u^{(0)}(t),\ldots,u^{(m-1)}(t)))
\end{align*}
$$
The \( \theta \)-rule
$$
\begin{equation}
\frac{u^{n+1}-u^n}{\Delta t} = \theta f(u^{n+1},t_{n+1}) +
(1-\theta)f(u^n, t_n)
\tag{38}
\end{equation}
$$
Bringing the unknown \( u^{n+1} \) to the left-hand side and the known terms
on the right-hand side gives
$$
\begin{equation}
u^{n+1} - \Delta t \theta f(u^{n+1},t_{n+1}) =
u^n + \Delta t(1-\theta)f(u^n, t_n)
\end{equation}
$$
This is a nonlinear equation in \( u^{n+1} \) (unless \( f \) is linear in \( u \))!
Implicit 2-step backward scheme
$$ u'(t_{n+1}) \approx \frac{3u^{n+1} - 4u^{n} + u^{n-1}}{2\Delta t}$$
Scheme:
$$ u^{n+1} = \frac{4}{3}u^n - \frac{1}{3}u^{n-1} +
\frac{2}{3}\Delta t f(u^{n+1}, t_{n+1})
\tag{39}
$$
Nonlinear equation for \( u^{n+1} \).
The Leapfrog scheme
Idea:
$$
\begin{equation}
u'(t_n)\approx \frac{u^{n+1}-u^{n-1}}{2\Delta t} = [D_{2t} u]^n
\end{equation}
$$
Scheme:
$$ [D_{2t} u = f(u,t)]^n$$
or written out,
$$
\begin{equation}
u^{n+1} = u^{n-1} + \Delta t f(u^n, t_n)
\tag{40}
\end{equation}
$$
- Some other scheme must be used as starter (\( u^1 \)).
- Explicit scheme - a nonlinear \( f \) (in \( u \)) is trivial to handle.
- Downside: Leapfrog is always unstable after some time.
The filtered Leapfrog scheme
After computing \( u^{n+1} \), stabilize Leapfrog by
$$
\begin{equation}
u^n\ \leftarrow\ u^n + \gamma (u^{n-1} - 2u^n + u^{n+1})
\tag{41}
\end{equation}
$$
2nd-order Runge-Kutta scheme
Forward-Euler + approximate Crank-Nicolson:
$$
\begin{align}
u^* &= u^n + \Delta t f(u^n, t_n),
\tag{42}\\
u^{n+1} &= u^n + \Delta t \half \left( f(u^n, t_n) + f(u^*, t_{n+1})
\right)
\tag{43}
\end{align}
$$
4th-order Runge-Kutta scheme
- The most famous and widely used ODE method
- 4 evaluations of \( f \) per time step
- Its derivation is a very good illustration of numerical thinking!
2nd-order Adams-Bashforth scheme
$$
\begin{equation}
u^{n+1} = u^n + \half\Delta t\left( 3f(u^n, t_n) - f(u^{n-1}, t_{n-1})
\right)
\tag{44}
\end{equation}
$$
3rd-order Adams-Bashforth scheme
$$
\begin{equation}
u^{n+1} = u^n + \frac{1}{12}\left( 23f(u^n, t_n) - 16 f(u^{n-1},t_{n-1})
+ 5f(u^{n-2}, t_{n-2})\right)
\tag{45}
\end{equation}
$$
The Odespy software
Odespy features simple Python implementations of the most fundamental schemes as well as Python interfaces to several famous packages for solving ODEs: ODEPACK, Vode, rkc.f, rkf45.f, Radau5, as well as the ODE solvers in SciPy, SymPy, and odelab.
Typical usage:
# Define right-hand side of ODE
def f(u, t):
return -a*u
import odespy
import numpy as np
# Set parameters and time mesh
I = 1; a = 2; T = 6; dt = 1.0
Nt = int(round(T/dt))
t_mesh = np.linspace(0, T, Nt+1)
# Use a 4th-order Runge-Kutta method
solver = odespy.RK4(f)
solver.set_initial_condition(I)
u, t = solver.solve(t_mesh)
Example: Runge-Kutta methods
solvers = [odespy.RK2(f),
odespy.RK3(f),
odespy.RK4(f),
odespy.BackwardEuler(f, nonlinear_solver='Newton')]
for solver in solvers:
solver.set_initial_condition(I)
u, t = solver.solve(t)
# + lots of plot code...
Plots from the experiments
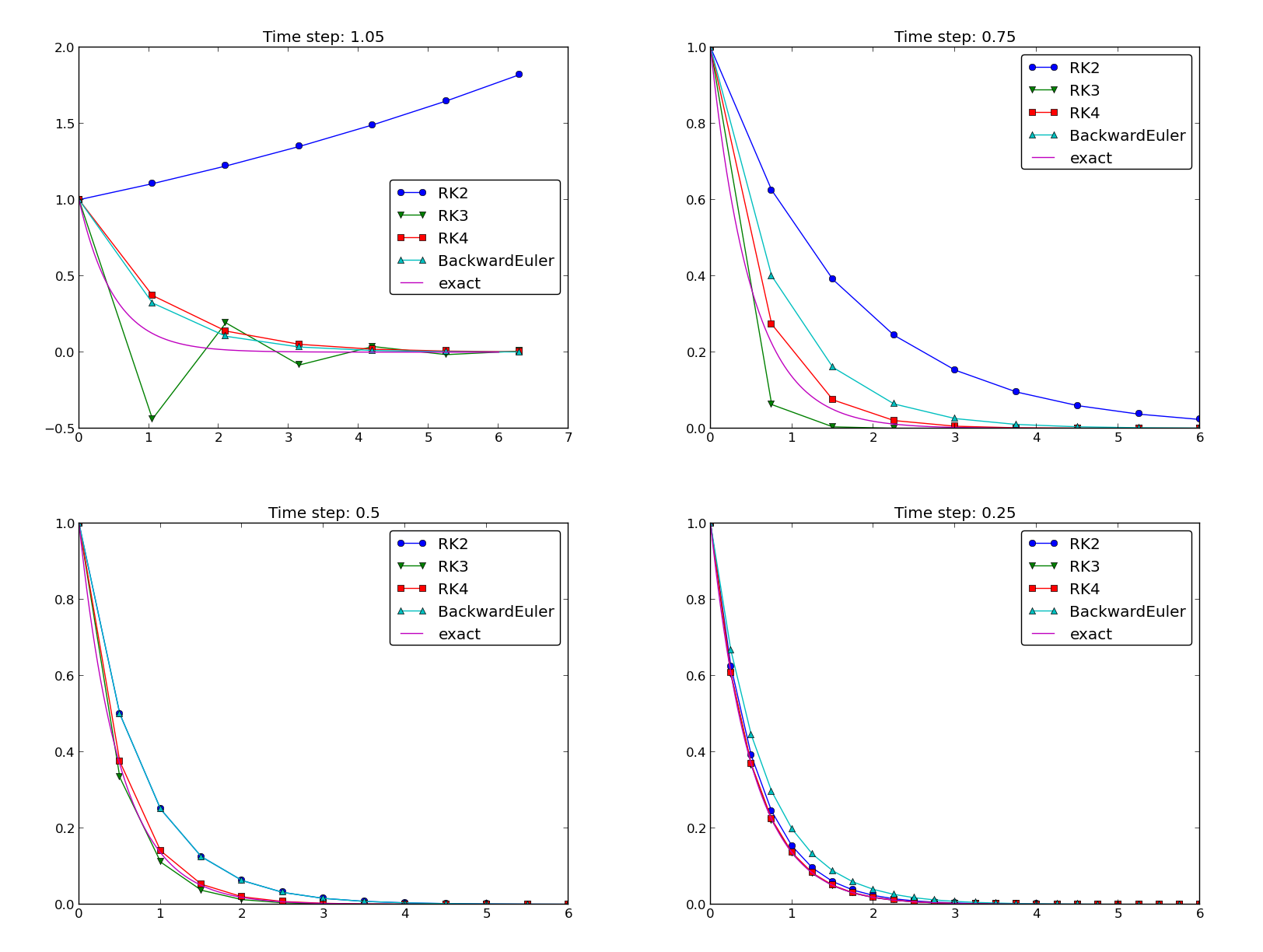
The 4-th order Runge-Kutta method (RK4) is the method of choice!
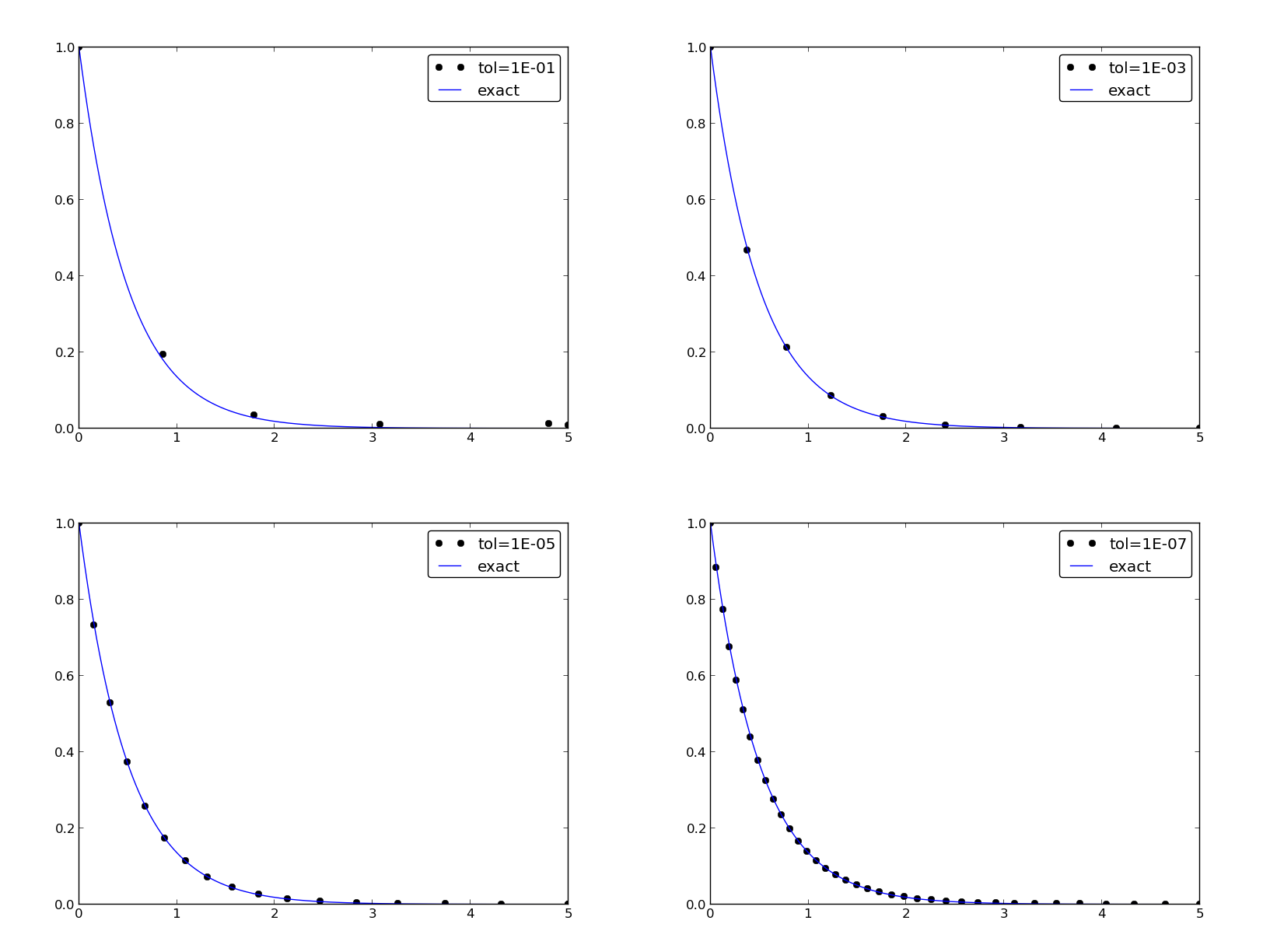
Example: Adaptive Runge-Kutta methods
- Adaptive methods find "optimal" locations of the mesh points to ensure that the error is less than a given tolerance.
- Downside: approximate error estimation, not always optimal location of points.
- "Industry standard ODE solver": Dormand-Prince 4/5-th order
Runge-Kutta (MATLAB's famous
ode45).